3. 2. 3 交换
交换两个数的位置,下面的函数需要用到。
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
3. 2. 4 入堆与向上调整函数
这里就是堆和顺序表不同的部分了。
如果我们想向堆中加入一个数据,该怎么做?
直接将它放进数组就完成了吗?
当然不行,为了确保在插入一个数据之后这个数组还能表示一个堆,我们需要先实现一个向上调整算法,在向顺序表插入新数据后,将这个数据向上调整到合适的位置来确保堆的正确。
void AdjustUp(HPDataType* arr, int child);
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
参数arr是堆的底层数组,参数child是要向上调整的数据。
要怎么向上调整?
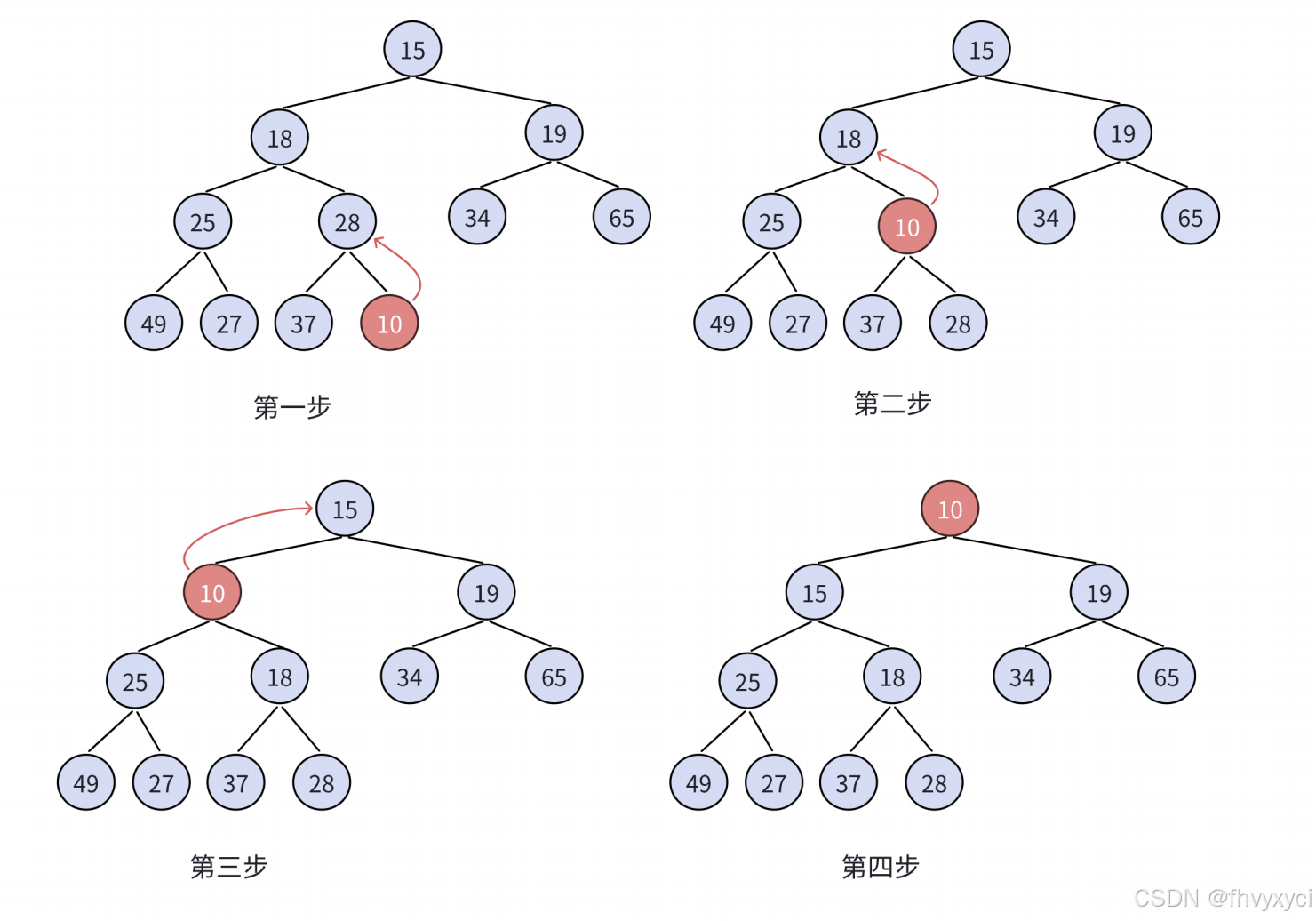
我们可以找到child的父节点parent,如果parent对应的数据比child小,就说明现在已经不用再进行调整了,堆已经正确了。如果如果parent对应的数据比child大,就交换这两个数。如果调整一次之后堆仍然不正确,就继续上面的步骤直到堆正确。
如图:
void AdjustUp(HPDataType* arr, int child)
{
assert(arr);
int parent = (child - 1)/2;
while (child)
{
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}"> class="hide-preCode-box">
接下来看入堆:
有以下两个步骤:
- 参考顺序表向数组尾插数据
- 向上调整
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 2 : 2 * hp->capacity;
HPDataType* new = (HPDataType*)realloc(hp->arr, newcapacity * sizeof(HPDataType));
if (!new)
{
perror("realloc");
exit(1);
}
hp->arr = new;
hp->capacity = newcapacity;
}
hp->arr[hp->size++] = x;
AdjustUp(hp->arr, hp->size - 1);
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}"> class="hide-preCode-box">
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
3. 2. 5 判空与取堆顶数据与堆的大小
判空
bool HeapEmpty(Heap* hp)
{
assert(hp);
return hp->size == 0;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
取堆顶数据
注意堆顶的下标是0。
HPDataType HeapTop(Heap* hp)
{
assert(hp && hp->size);
return hp->arr[0];
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
堆的大小
int HeapSize(Heap* hp)
{
assert(hp);
return hp->size;
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
3. 2. 6 出堆与向下调整
堆这个数据结构如果要删除数据只能从堆顶删除(可以类比现实中的堆,肯定不能从中间抽数据,不然堆就塌了)。那该怎么删除数据呢?
直接将堆顶元素删除吗?如果是这样,就要把后面所有元素向前挪动一位,而且两个孩子节点谁当父节点也是个问题。(在纸上画一画,很容易会发现这样删除真的很复杂)
所以更合适的办法应该是将堆顶元素与堆的最后一个元素交换位置,将最后一个元素删除,再进行向下调整算法。
void AdjustDown(HPDataType* arr, int parent, int n);
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
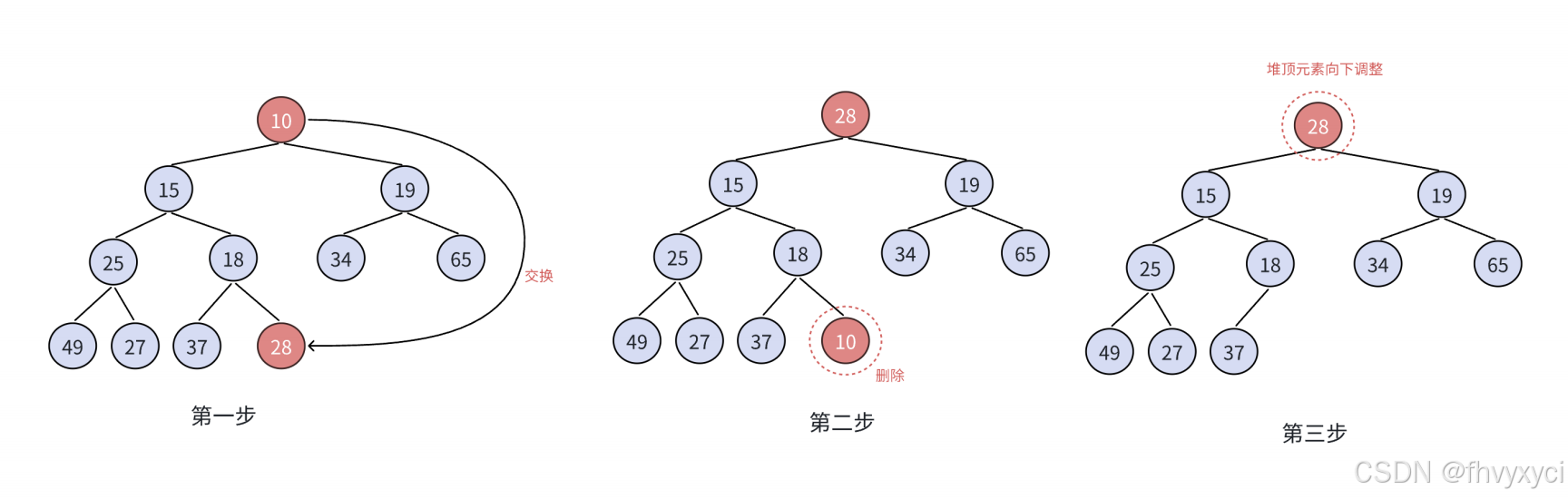
向下调整和向上调整的思想是一样的,都是通过比较父节点与孩子节点并交换,直到堆是正确的。
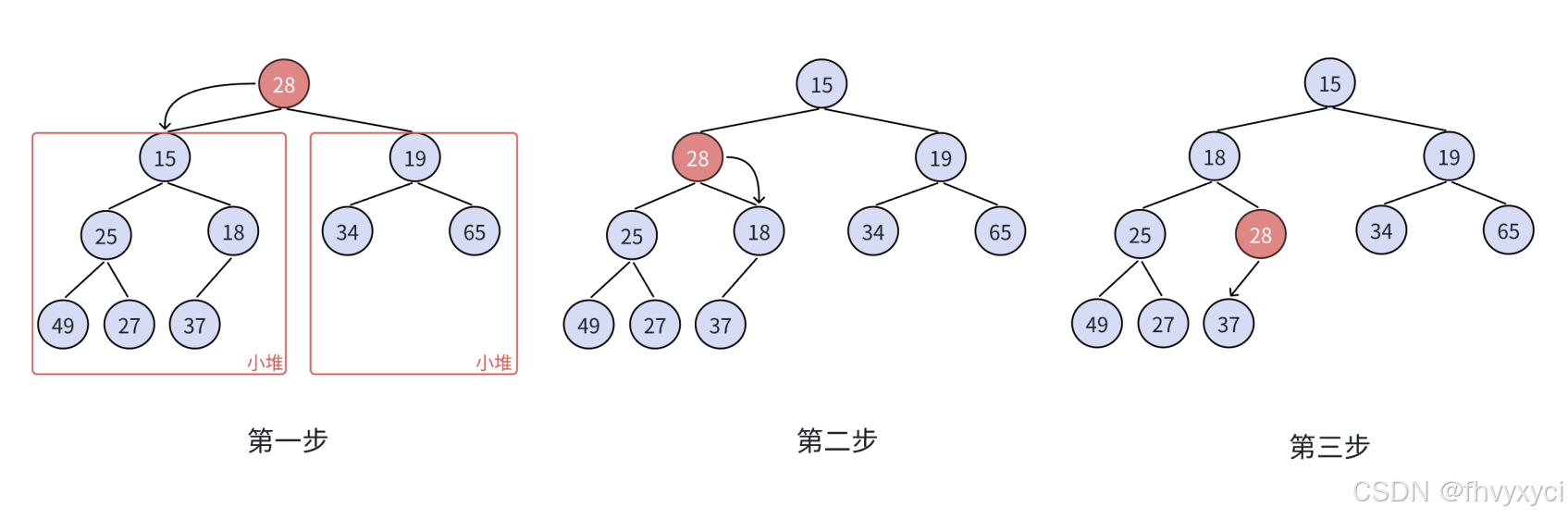
注意这里父节点应该和较小的孩子节点进行比较与交换,来确保交换(如果发生交换)之后父节点大于孩子节点。
向下调整算法还有一个前提:左右子树必须是一个堆,才能调整。也就是说在调整之前,除了堆顶元素外,堆必须是正确的。
void AdjustDown(HPDataType* arr, int parent, int n)
{
assert(arr);
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && arr[child] > arr[child + 1])
child++;
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
break;
}
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}"> class="hide-preCode-box">
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
接下来就是出堆的完整函数了:
void HeapPop(Heap* hp)
{
assert(hp && hp->size);
Swap(&hp->arr[0], &hp->arr[hp->size - 1]);
hp->size--;
AdjustDown(hp->arr, 0, hp->size);
}
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
3. 2. 7 大堆
实现小堆之后,只需要在两个调整算法中更改一下调整的判断条件(比如原来是父节点比子节点大就交换,更改成父节点比子节点小就交换)就能实现大堆了,这里就不再赘述了。
谢谢你的阅读,喜欢的话来个点赞收藏评论关注吧!
我会持续更新更多优质文章
data-report-view="{"mod":"1585297308_001","spm":"1001.2101.3001.6548","dest":"https://blog.csdn.net/fhvyxyci/article/details/142302787","extend1":"pc","ab":"new"}">>







评论记录:
回复评论: