LeetCode | 图文详细描述动态规划DP算法及经典题型

本文将用简单直白的方式，从零开始带你掌握动态规划的精髓。你会发现：

  • 动态规划其实没那么难——它就是递归的“记性”版。
  • 状态转移方程不再玄学——从题目思路到实现，手把手教你推导。
  • 经典题型剖析——从“爬楼梯”到“背包问题”，全都有图、有代码、有思路。

看完这篇文章，动态规划不再是拦路虎，而是你刷题路上的好伙伴。现在，准备好解锁 DP 的魔法了吗？Let's go! ?

1.理论

1.1. 动态规划的定义

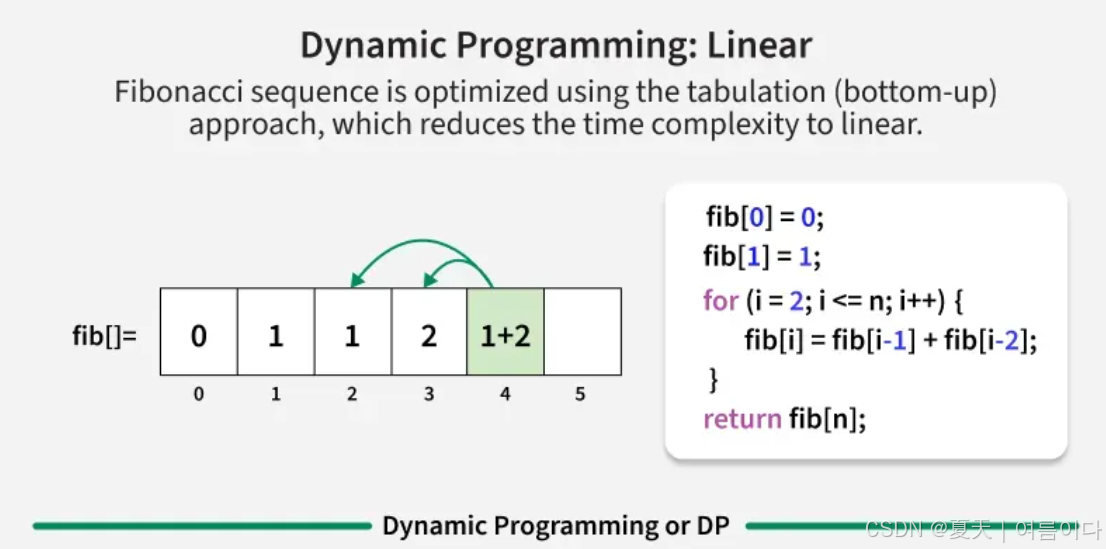
动态规划（Dynamic Programming, DP）是一种通过将问题分解为更小的子问题，逐步求解并存储中间结果，从而避免重复计算的优化方法。它适用于具有 重叠子问题 和 最优子结构 的问题。

1.2. 动态规划的关键特性

 1.2.1.重叠子问题（Overlapping Subproblems）

 问题可以分解为许多重复的子问题。例如：

斐波那契数列问题中：F(n) = F(n-1) + F(n-2)，子问题重复出现。

1.2.2.最优子结构（Optimal Substructure）

一个问题的最优解由其子问题的最优解构成。例如： 

爬楼梯问题：到达第 nnn 级的总方法数是第 n−1n-1n−1 和第 n−2n-2n−2 级方法数之和。 

1.2.3.状态转移方程（State Transition Equation）

描述如何从子问题的解构建更大问题的解，是动态规划的核心。例如： 

背包问题的状态转移方程：dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i]] + value[i])

1.3. 动态规划的常见步骤

1.3.1.定义状态（State）
用一个数组或矩阵 dp 表示问题的解，其中 dp[i] 或 dp[i][j] 表示问题在第 i或 (i,j) 状态的最优解。

1.3.2.状态转移方程（State Transition Equation）
找到子问题与原问题的递推关系，确定状态如何从前一个状态转移。

1.3.3.初始化（Initialization）
确定基础情况，例如：dp[0] 或 dp[0][0]。

1.3.4.递推计算（Iteration）
通过循环从基础状态逐步递推到目标状态。

1.3.5.返回结果（Result Extraction）
最终返回 dp[n] 或 dp[m][n] 等目标状态的值。

1.4. 动态规划的分类

1.4.1.一维动态规划

问题：斐波那契数列、爬楼梯、最小花费爬楼梯

特点：状态数组为一维，dp[i] 表示第 iii 步的解。

示例：爬楼梯 dp[i]=dp[i−1]+dp[i−2]

1.4.2.二维动态规划

问题：最短路径问题、背包问题、字符串匹配问题

特点：状态数组为二维矩阵，dp[i][j] 表示二维状态。

示例：最小路径和 dp[i][j]=grid[i][j]+min⁡(dp[i−1][j],dp[i][j−1])

1.4.3.区间动态规划

问题：矩阵链乘积、回文分割问题

特点：状态表示为区间，dp[i][j] 表示从第 iii 到第 jjj 的最优解。

示例：最长回文子序列 dp[i][j]=dp[i+1][j−1]+2if s[i]==s[j]dp[i][j] = dp[i+1][j-1] + 2 \quad \text{if } s[i] == s[j]dp[i][j]=dp[i+1][j−1]+2if s[i]==s[j]

1.4.4.背包动态规划

问题：01背包问题、完全背包问题

特点：根据背包容量和物品状态转移。

示例：01背包问题 dp[i][w]=max⁡(dp[i−1][w],dp[i−1][w−weight[i]]+value[i])

1.4.5.记忆化递归

问题：与普通动态规划类似，但通过递归解决，配合缓存（如字典或数组）存储中间结果。

特点：自顶向下的方式求解，与自底向上的普通 DP 思路相反。

1.5. 优化技巧

1.5.1.空间优化

如果状态转移只依赖前几步状态，可以通过滚动数组将空间复杂度从 O(n)O(n)O(n) 降低到 O(1)O(1)O(1)。

示例：斐波那契数列优化版本只用两个变量 prev2 和 prev1。

1.5.2.压缩维度

对于二维动态规划问题，可以压缩到一维数组进行状态存储。

示例：01 背包问题中，用一维数组存储容量状态。

1.5.3。减少不必要计算

通过提前剪枝，减少动态规划状态的计算范围。

总结：动态规划是一种递推式的优化算法，旨在以最少的计算解决递归性质的问题。

2.真题

2.0.基本

第 N 个斐波那契数

给定一个正整数 n，任务是找到第 n 个斐波那契数。

斐波那契数列是其中一项是前两项之和的序列。斐波那契数列的前两项是 0 后跟 1。斐波那契数列：0、1、1、2、3、5、8、13、21

斐波那契数定义：
  1. F(0)=0
  2. F(1)=1
  3. F(n)=F(n−1)+F(n−2)（当 n≥2）

例：

输入：n = 2
输出：1
说明：1 是斐波那契数列的第 2 个数字。

输入：n = 5
输出：5
说明：5 是斐波那契数列的第 5 个数字。

解题思路：

  1. #方法1：递归，时间复杂度：O(2^n) 和 空间复杂度：O(n)
  2. def nth_fibonacci(n):
  3. # 函数 nth_fibonacci(n) 用于计算第 n 个斐波那契数。
  4.  
  5.     if n<=1:
  6.         return n
  7.     
  8.     return nth_fibonacci(n-1)+nth_fibonacci(n-2)
  9.  
  10.  
  11. n=5
  12. result=nth_fibonacci(n)
  13. print(result)
  14.  
  15.  
  16. #方法2：自下而上的迭代法 就是计算斐波那契数的最优解法
  17.  
  18. def nth_fibonacci(n):
  19.     if n<=1:
  20.         return n
  21.  
  22.     prev2=0
  23.     prev1=1
  24.  
  25.     for _ in range(2,n+1)：
  26.         curr=prev1+prev2
  27.         prev2=prev1
  28.         prev1=curr
  29.     return prev1
  30.  
  31. if __name__=="__main__"：
  32.     n=5
  33.     rusult=nth_fibonacci(n)
  34.     print(n)
  35.  
  36. ######## 方法最优性分析 ########
  37. 时间复杂度：O(n):只需一次从 2 到 n 的循环，每次循环进行常数操作。
  38. 空间复杂度：O(1):只用到了三个变量：prev2, prev1, 和 curr，不需要额外的数组存储所有结果。
  39. 优点
  40. 节省空间：将空间复杂度从O(n) 降低到 O(1)。
  41. 简洁高效：代码简洁明了，计算速度快。
  42.  
  43.  
  44.  
  45.  
  46.  
  47.  
  48.  
  49.  
  50. #方法3：自上而下的方法 时间复杂度：O(n) 和 空间复杂度：O(n)
  51. def nth_fibonacci(n):
  52.     if n<=1:
  53.         return n
  54.  
  55.     dp=[0]*(n+1)
  56.     # 创建一个长度为n+1 的数组 dp，用来存储从 F(0) 到 F(n) 的结果。
  57.     dp[0]=0
  58.     dp[1]=1
  59.     # 初始化已知的F(0)=0,F(1)=1
  60.     
  61.     for i in range(2,n+1):
  62.     #遍历i从2到n
  63.         dp[i]=dp[i-1]+dp[i-2]
  64.     return dp[n]
  65.     #每次迭代都将迭代结果存储到dp[i]中，避免重复计算。
  66.  
  67.  
  68. if __name__=="__main__":
  69.     n=5
  70.     result=nth_fibonacci(n)
  71.     print(result)
  72.  
  73.  
  74. #动态规划方法通过迭代计算，只需遍历一次从 2 到 n 的范围，每次计算都只涉及常数操作，因此时间复杂度是 O(n)。
  75.  
  76. #使用了一个大小为n+1 的数组 dp 来存储中间计算结果，占用线性空间。

需掌握题型

  • 爬楼梯（Climbing Stairs）
  • 最大子数组和（Maximum Subarray, Kadane's Algorithm）
  • 最长递增子序列（Longest Increasing Subsequence, LIS）
  • 背包问题（01背包、完全背包）
  • 编辑距离（Edit Distance）

2.1.简单

【Leetcode70】爬楼梯 Climbing Stairs

 定义问题：有 n 级楼梯，每次可以走 1 步或 2 步，求到达顶楼的总方法数。

  1. def climb_stairs_optimized(n):
  2.     if n<=1:
  3.         return 1
  4.     
  5.     #初始化两个变量，用来存储最近两次计算结果
  6.     prev2=1 #代表 f(n−2)，初始值为 1
  7.     prev1=1 代表 f(n−1)，初始值为 1
  8.  
  9.  
  10.     #迭代计算斐波那契数列
  11.     for _ in range(2,n+1):  #使用一个循环，从第 2 阶楼梯计算到第n阶楼梯
  12.  
  13.         curr=prev1+prev2 #当前楼梯的方法数，由前两阶的和决定 
  14.  
  15.         prev2=prev1 #将 prev1（即 f(n−1)）赋值给 prev2
  16.  
  17.         prev1=curr  # 将 curr（即 f(n)）赋值给 prev1。 这样 prev1 和 prev2 始终保存最近的两次计算结果。
  18.  
  19.     return prev1 #循环结束时，prev1 存储的是 f(n)，即到达第 n 阶的方法数。
  20.  
  21.  
  22. if __name__="__main__":
  23.     n=5
  24.     print("ways to climb stairs:", climb_stairs_optimized)

运行过程：

假设 n=5，步骤如下：

Iterationprev2 (f(n−2))prev1 (f(n−1))curr (f(n))
初始值01-
n=2n=2n=2111
n=3n=3n=3122
n=4n=4n=4233
n=5n=5n=5355

最终，prev1 = 5，表示爬到第 5 阶的方法数为 5。

时间与空间复杂度分析

时间复杂度：O(n)

  • 无论使用 O(n) 空间还是 O(1) 空间，算法都只需要一次从 2 到 n的迭代。

空间复杂度：

  1. 使用数组 O(n)：需要额外数组存储中间结果。
  2. 空间优化 O(1)：仅存储两个变量，节省了内存。

2.2.中等

【Leetcode53】最大子数组(Maximum Subarray)

问题：给定一个整数数组，找到nums子数组，并返回其总和

  1. def max_subarray(nums):
  2.     current_sum=max_sum=nums[0] # 初始化 current_sum 和 max_sum 为数组的第一个元素
  3.     # 第一个元素已经处理过
  4.  
  5.     for i in range(1,len(nums)): # 从第二个元素开始遍历
  6.     
  7.         current_sum=max(nums[i],current_sum+nums[i]) # 当前子数组的最大和
  8.     
  9.         max_sum=max(max_sum,current_sum) # 更新全局最大和
  10.  
  11.     return max_sum
  12.  
  13. if __name__=="__main__":
  14.     nums=[-2,1,-3,4,-1,2,1,-5,4]
  15.     print("最大子数组和：",max_subarray(nums))

 运行过程：

数组：nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]

元素current_sum 更新规则current_summax_sum
-2初始值-2-2
1max(1, -2 + 1) = 111
-3max(-3, 1 - 3) = -2-21
4max(4, -2 + 4) = 444
-1max(-1, 4 - 1) = 334
2max(2, 3 + 2) = 555
1max(1, 5 + 1) = 666
-5max(-5, 6 - 5) = 116
4max(4, 1 + 4) = 556

 最优性分析：

  • 时间复杂度最优：只需一次遍历，时间复杂度为 O(n)。
  • 空间复杂度最低：不需要额外存储，只用常数级变量，空间复杂度为 O(1)。
  • 适用性强：适用于有正负数混合的数组，且数组长度为 1 时依然有效。

【Leetcode64】网格中的最小路径/最小路径总和（Minimux Path Sum）

给定一个2d矩阵成本[][]，任务是计算从（0， 0）到（m，n）的最小成本路径。矩阵的每个像元都表示求解该像元的成本。到达路径的总费用（米，N）是该路径（包括源和目标）上所有费用的总和。我们只能从给定的单元格依次、向右和对角线依次遍历单元格，即从给定的单元格开始单元格 （i，j）、单元格（i+1，j）、（i，j+1）和（i+1，j+1）可以遍历。

问题分析：

要找到从左上角 (0, 0) 到右下角 (m, n) 的最小成本路径，可以使用 动态规划。动态规划是一种有效的方法，它通过记录每一步的最优结果，避免了重复计算。

动态规划的最优解

我们定义一个辅助的动态规划矩阵 dp，其中 dp[i][j] 表示从 (0, 0) 到 (i, j) 的最小成本路径。转移方程如下：

dp[i][j]=cost[i][j]+min⁡(dp[i−1][j],dp[i][j−1],dp[i−1][j−1])

  1. def min_cost_path(cost,m,n):
  2.     rows=len(cost)
  3.     cols=len(cost[0])
  4.     
  5.     # 创建动态规划矩阵
  6.     dp=[[0]*clos for _ in range(rows)]
  7.  
  8.     # 初始化起点
  9.     dp[0][0]=cost[0][0]
  10.  
  11.     # 初始化第一行
  12.     for j in range(1,cols):
  13.         dp[0][j]=dp[0][j-1]+cost[0][j]
  14.     
  15.     # 初始化第一列
  16.     for i in range(1,rows):
  17.         dp[i][0]=dp[i-1][0]+cost[i][0]
  18.  
  19.     
  20.     # 填充剩余的 dp 矩阵
  21.     for i in range(1,rows):
  22.         for j in range(1,cols):
  23.         dp[i][j]=cost[i][j]+min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])
  24.  
  25.     # 返回右下角的最小成本路径
  26.     return dp[m][n]
  27.  
  28. if __name__ == "__main__":
  29.     cost = [
  30.         [1, 2, 3],
  31.         [4, 8, 2],
  32.         [1, 5, 3]
  33.     ]
  34.     m, n = 2, 2  # 目标位置
  35.     result = min_cost_path(cost, m, n)
  36.     print("Minimum cost path:", result)

最优性分析：

时间复杂度：O(m×n)

  • 需要遍历整个矩阵，每个单元格计算一次。

空间复杂度：O(m×n)

  • 需要额外的 dp 矩阵存储中间结果。

参考文献

[1]A Beginner's Guide to Dynamic Programming

[2]Dynamic Programming or DP - GeeksforGeeks

注：本文转载自blog.csdn.net的夏天｜여름이다的文章"https://blog.csdn.net/weixin_44649780/article/details/145140378"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！