shigen坚持更新文章的博客写手,擅长Java、python、vue、shell等编程语言和各种应用程序、脚本的开发。记录成长,分享认知,留住感动。
hello,伙伴们又有几天的时间不见了。
我的文章也要改变一下日更的策略了,变成坚持更新了。有很多因素的影响,我希望能继续为伙伴们带来精彩的文章。
那就直接开始今天的正题吧。在shigen之前的文章开源一个局域网文件共享工具中有提到了我设计的局域网文件共享工具,实现扫码即可上传文件,访问链接直接下载文件。在我的github上也成功的获得了5和star。5个star我觉得已经很满足了,毕竟我也是第一次尝试做开源。
那今天为什么又要提这个项目呢?因为它迎来了大更新:
- 语言的成分占比:html占比51%,python已经不是主要的开发语言了
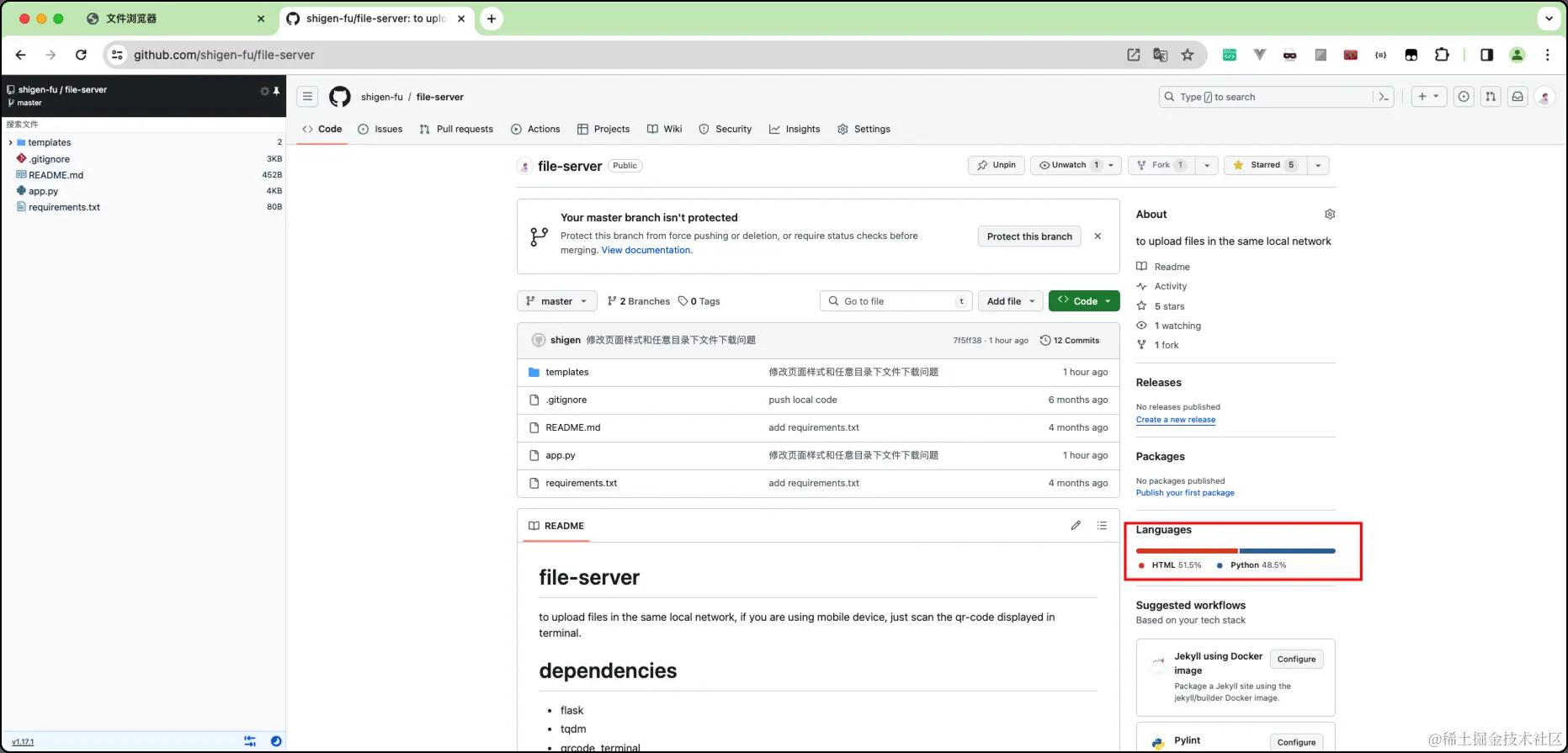
这意味着我本次对代码的前端样式做了更大的调整。接下来我会详细的展示。
- 主页新增了两个按钮
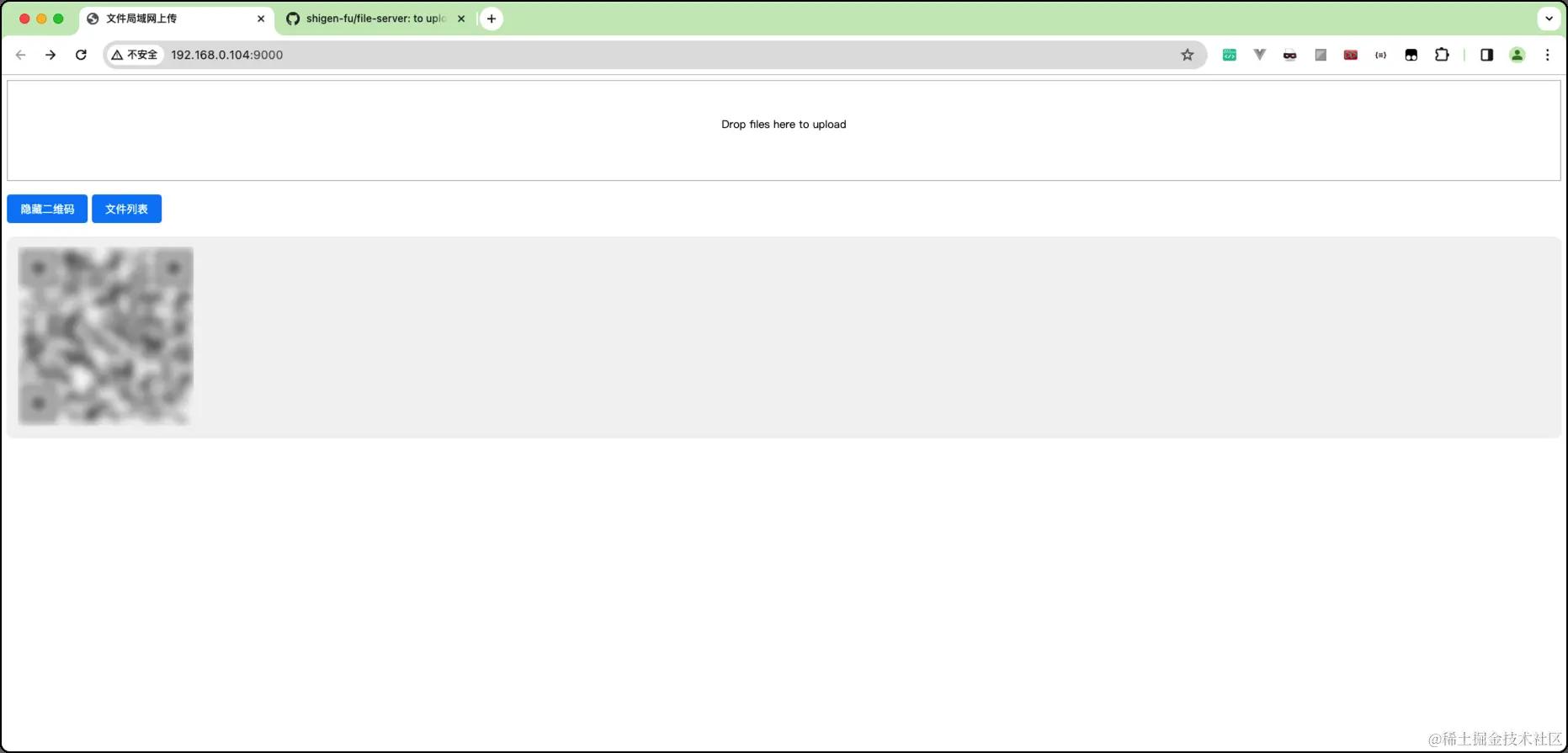
这里可以展示/隐藏访问的二维码(默认不展示二维码),同时,点击文件列表,即可跳转到文件的列表页。
- 优化文件列表页,展示更多的文件、文件夹信息
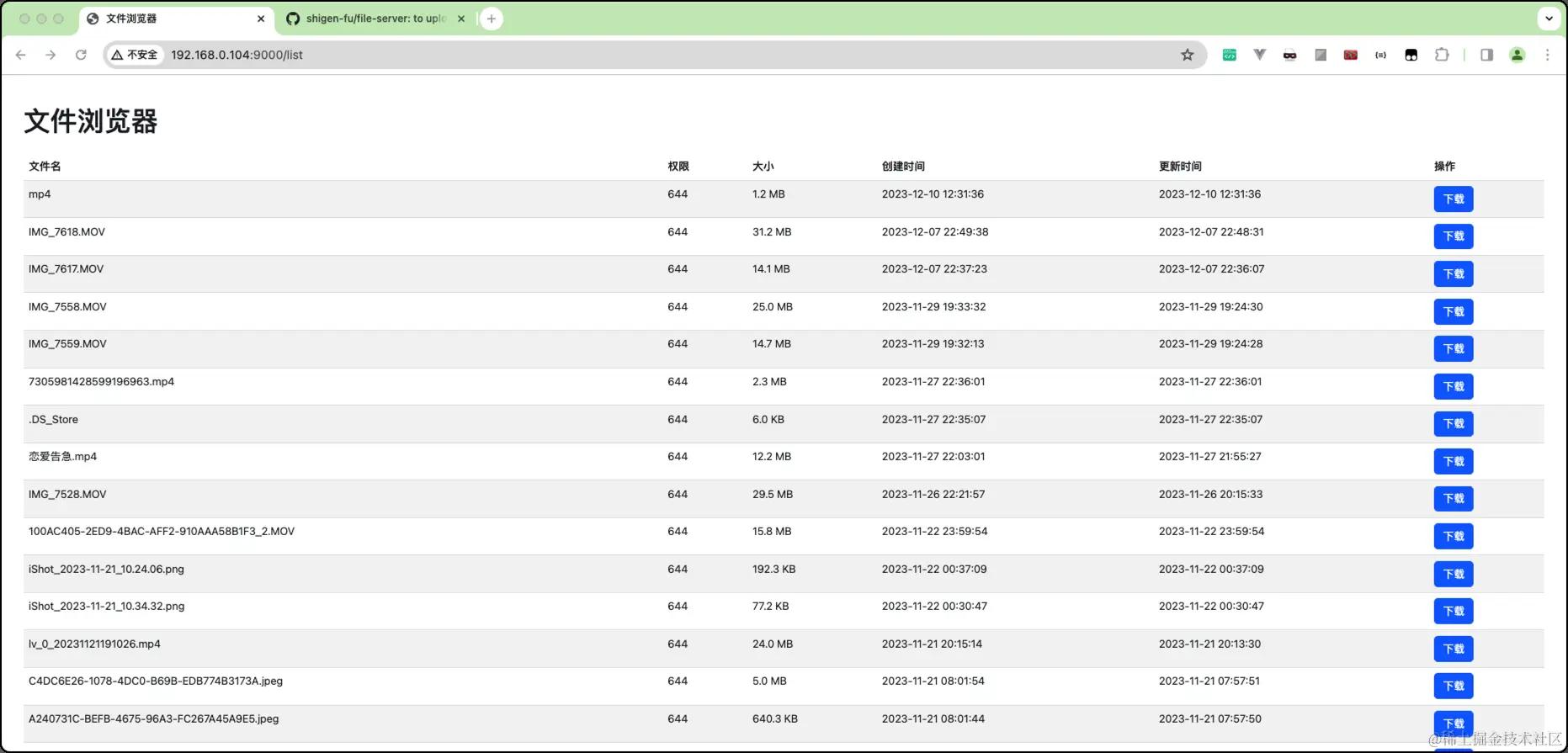
可以看到此次的更新中,我我们展示了更多的文件信息:如文件的权限、文件的大小、更新时间等,同时根据更新时间降序排列。这意味着我们最新上传的文件会放在最上边展示。
- 文件夹下的文件可以下载了

之前的文件夹下的文件下载其实有bug的,一直没有得到解决的办法。今天看了一下代码,突然的就灵机一动,发现了解决的办法。现在,我们可以下载静态资源文件夹下的任何文件夹下的任何文件了。
以上就是本次项目的全部更新了,用起来效果会更好了。也欢迎伙伴们给我提建议,将这个项目做的更好。
欢迎伙伴们体验服务,只需要一行代码:
bash复制代码 git clone https://github.com/shigen-fu/file-server.git && cd file-server && pip install -r requirements.txt && python app.py
以上就是今天分享的全部内容了,觉得不错的话,记得点赞 在看 关注支持一下哈,您的鼓励和支持将是shigen坚持日更的动力。同时,shigen在多个平台都有文章的同步,也可以同步的浏览和订阅:
| 平台 | 账号 | 链接 |
|---|---|---|
| CSDN | shigen01 | shigen的CSDN主页 |
| 知乎 | gen-2019 | shigen的知乎主页 |
| 掘金 | shigen01 | shigen的掘金主页 |
| 腾讯云开发者社区 | shigen | shigen的腾讯云开发者社区主页 |
| 微信公众平台 | shigen | 公众号名:shigen |

与shigen一起,每天不一样!
前言
什么是差分约束
x系列是变量,y系列是常量,差分系统由若干如下不等式组成。
x1-x2 <= y1 x2-x3 <= y2
⋯
\cdots
⋯
可能有负环的最短路
个人习惯:如果存在a指向b的边,则a是b的前置节点,b是a的后续节点。
某差分约束有n个变量(编号从1到n),m个不等式。根据此差分约束建立有向图G。
第一步,n个节点,m条边。每个不等式
x
1
−
x
2
<
=
y
1
都增加边
x
2
→
x1 - x2 <=y1都增加边 x2 \rightarrow
x1−x2<=y1都增加边x2→x1,边权位y1。
第二步:增加节点0,0到所有节点都有边,边权为0。
差分系统的变量和0到各节点的最短路一一对应。
性质一:差分约束所有的限制,有向图都有。故:有向图的解一定是差分约束的解。差分约束的解不一定是G的最短路。
⟺
\iff
⟺ 差分系统是G的充分不必要条件。
性质二:有向图无解时,差分约束也无解。存在负环时,有向图无解。不失一般性,以3个节点的环为例。有向图有负环时,差分系统有: x1<=x2+y1 x2<=x3+y2 x3 <=x1+y3 x1 <= x1 + y1+y2+y3 即 0 <= y1+y2+y3,和节点1,2,3是负环矛盾。可以用数学归纳法证明。
性质三:令(a1,a2
⋯
\cdots
⋯)是有向图的解,则(a1+d,a2+d
⋯
\cdots
⋯)也是差分系统的解。因为:(x1+d)-(x2-d)等于x1-x2。
性质四:在不引入负环的前提下,缩短任意一条边的解仍然是原系统的解。将y1减去正无穷小(此边权变小),构成的新图。如果有解,也是旧系统的解。
推论一:将任何节点i的直接、间接前置节点和i增加一个正数,则新系统的解仍然是老系统的解。如果节点在环上,此环上所有节点都增加。由于环的点都增加了x,故环上的边权不变,故不会引入负环。
性质五:延长任意一条边产生的新解一定不是旧系统的解。产生的新解 x1-x2一定大于y1。
推论二:原始图,如果节点i增加了一个正整数x,则它的直接、间接前置节点都需要增加x或更多。
负环最短路
dis[t][cur]记录最多经过t条边,从0到cur的最短路。
∀
\forall
∀cur ,dis[n][cur] != dis[n-1][cur],说明存在负环。则无解。
第一层循环枚举前置状态,t = 0 to N-1。第二循环枚举各边。
时间复杂度:O(点数边数)
template<class T = int, T iDef = INT_MAX / 2>
class CDisNegativeRing //贝尔曼-福特算法
{
public:
bool Dis(int N, vector<tuple<int, int, int>> edgeFromToW, int start) {
vector<T> pre(N, iDef);
pre[start] = 0;
for (int t = 0; t < N; t++) {
auto cur = pre;
for (const auto& [u, v, w] : edgeFromToW) {
cur[v] = min(cur[v], pre[u] + w);
}
if (t + 1 == N) {
for (int i = 0; i < N; i++) {
if (pre[i] != cur[i]) { return false; }
}
}
pre.swap(cur);
}
m_vDis = pre;
return true;
}
vector<T> m_vDis;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
最长路
对应的差分系统是:x1-x2 >= y1 x2-x3 >=y2 x3-x1 >=y3
如果存在正环,则无解。
可以延长边,不能缩短边。
节点i和它的直接间接前置节点可以减去一个正数,仍然是解。
样例
| 【差分约束】P5960 差分约束 | 普及+ |
| 【差分约束】P4878 [USACO05DEC] Layout G | 普及+ |
| 如果差分系统无解,本题无解。如果有解,求第N个变量减第一个变量的最大值。如果1不是N的前置节点,则N可无限增大,即无穷大。否则就是最短路相减。 | |
| 【差分约束】P5590 赛车游戏 | 省选- |
| 本题求边权,任意解,即差分系统的y系列。 | |
| 【差分约束】 P3275 [SCOI2011] 糖果 | 省选- |
| 本题求最小正整数解,利用拓扑排序和推论一。 |
扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。
 QQ群名片
QQ群名片



评论记录:
回复评论: