推荐|工作量不断增加的微软Azure，正缩小与亚马逊AWS的差距

戳蓝字“CSDN云计算”关注我们哦！

640?wx_fmt=jpeg

一份来自富莱睿（Flexera）的《RightScale 2019年云计算现状报告》划出了当下企业云战略的关注重点：企业在云计算方面的支出增加，基于此，各企业重视对云支出进行优化。

根据全球知名软件资产管理提供商富莱睿（Flexera）发布的《RightScale 2019年云计算现状报告》，企业将逐步采用多云方案，而当中有一半的企业在公有云上的花费超过100万美元。与此同时，微软Azure的工作量继续增加，云方案的采用及云支出的优化仍然是2019年重要的主题。

这份来自RightScale的报告（以下简称为报告）采访了786位相关人士，其中有58%的受访者被归类为企业客户。在这之前，大数据分析公司Kentik和云资源管理公司Densify也相应做过类似的调查并同样强调“多云应用中的成本优化是关键议题”的观点。

2019年是把优化云支出作为当务之急的第三年，持有这一观点的比例也从2018年的58%增至64%。虽然64%的受访者将优化云支出列为首要举措，但这一比例在中高级云用户中更高，分别为70%和76%。

根据报告，平台即服务（PaaS）、无服务器（serverless）、机器学习和容器的使用等正在激增。

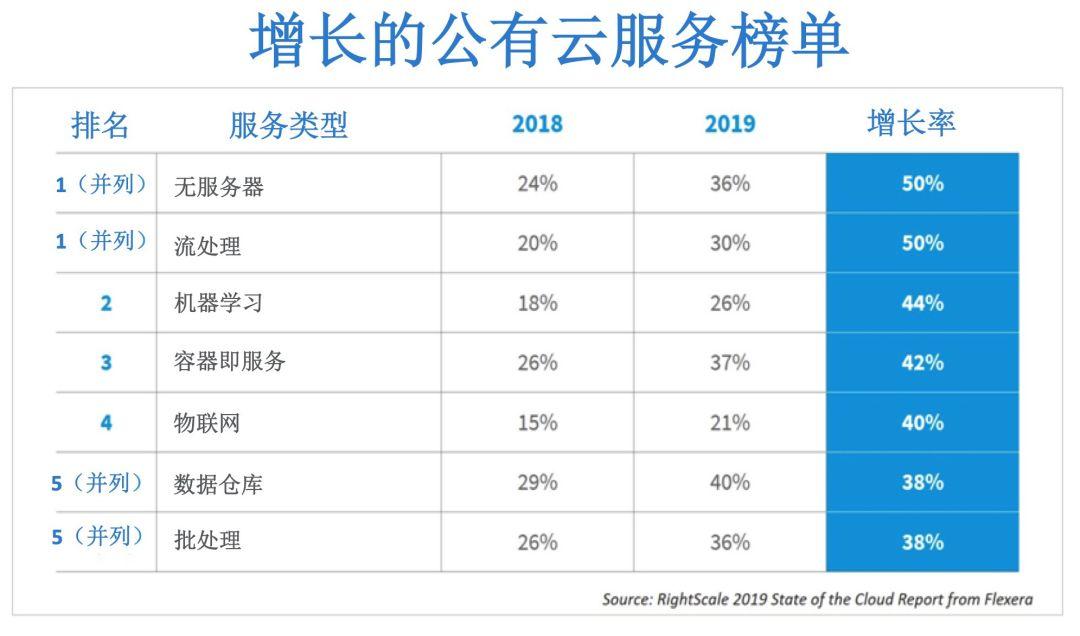640?wx_fmt=png 消息来源：富莱睿《RightScale 2019年云计算现状报告》

RightScale发现，84%的企业已在实施多云战略，其中有61%为中小企业。总的来说，RightScale报告的受访者平均使用4.9个公有云和私有云。

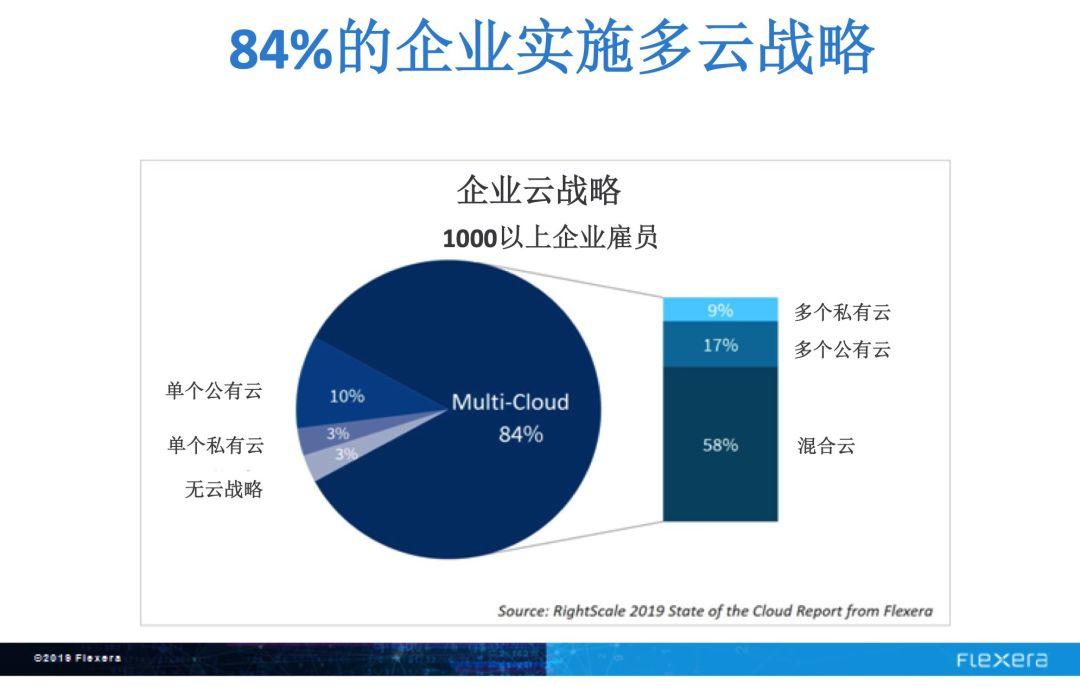
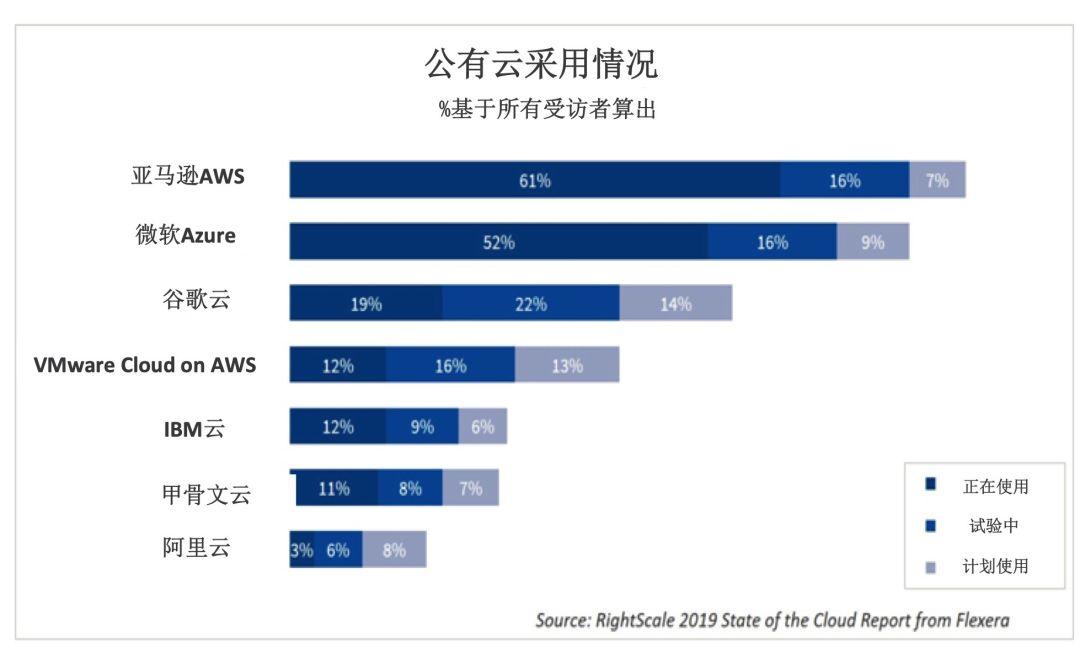
640?wx_fmt=png

企业在云支出增长主要原因是使用微软Azure。以下为RightScale关于这个结论的分析：

从总体来看，微软Azure采用率从之前的45%增长到52%，与亚马逊AWS之间的差距进一步缩小，目前Azure采用率已达到AWS采用率的85%，高于去年的70%。Azure在企业方面追赶AWS的增速最快，其中，Azure的采用率从58%略微增至60%，而AWS相应的采用率则相对平稳，为67%。谷歌则保持处于第三的排名，其采用率从18%略微增长至19%。自2018上市以来，AWS上的VMware Cloud采用率从上市第一年的8%上升到了今年的第四位，增长率达50%。报告在2018年对其他公有云提供商的调查中发现，今年这些提供商采用率均有所提高，甲骨文从10%增长到16%（增长率为60%），IBM云从15%增长到18%（增长率为20%），阿里云则从2%增长到4%（增长率为100%）。

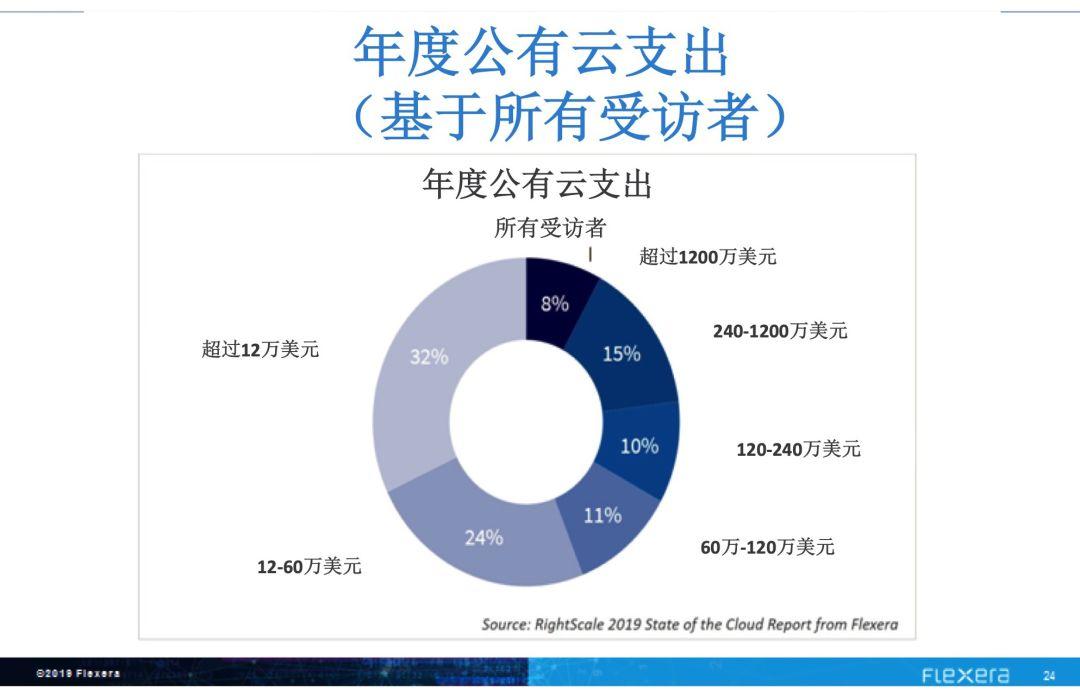
640?wx_fmt=png

随着对云计算支出的激增，其中一半的企业每年公有云支出超过120万美元，关于云支出的担忧也随之产生。根据报告，66%的企业已经创建了一个云中心团队来管理云服务。

根据RightScale调查发现，公司正在寻求在移动工作负载之上优化现有的云方案，由此可见，企业对云中心团队的部署主要出于成本管理的原因。

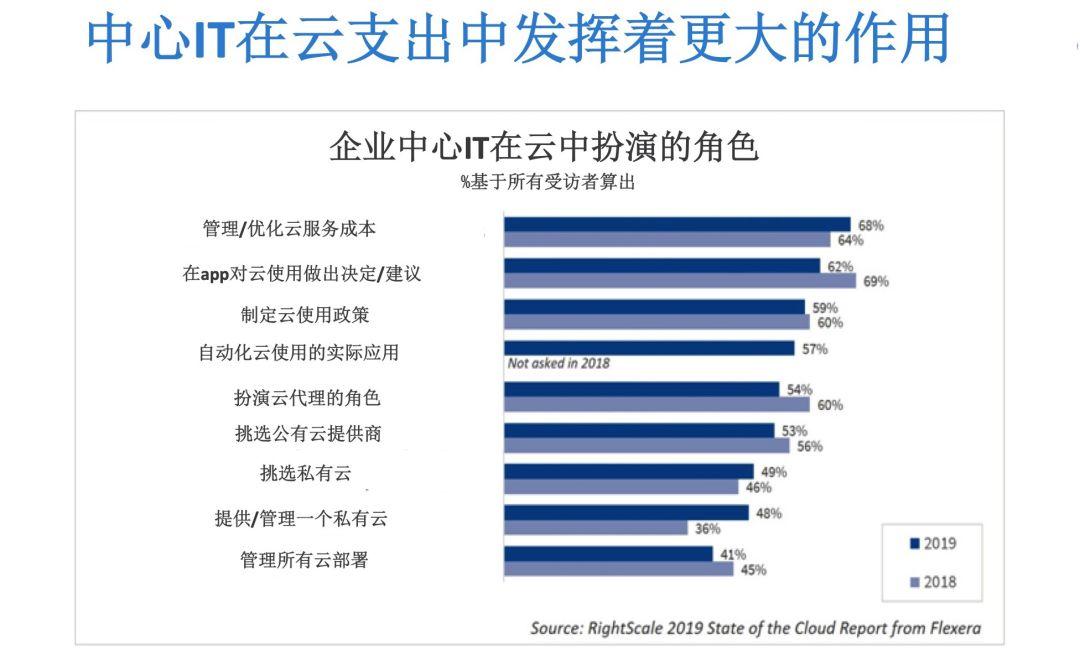
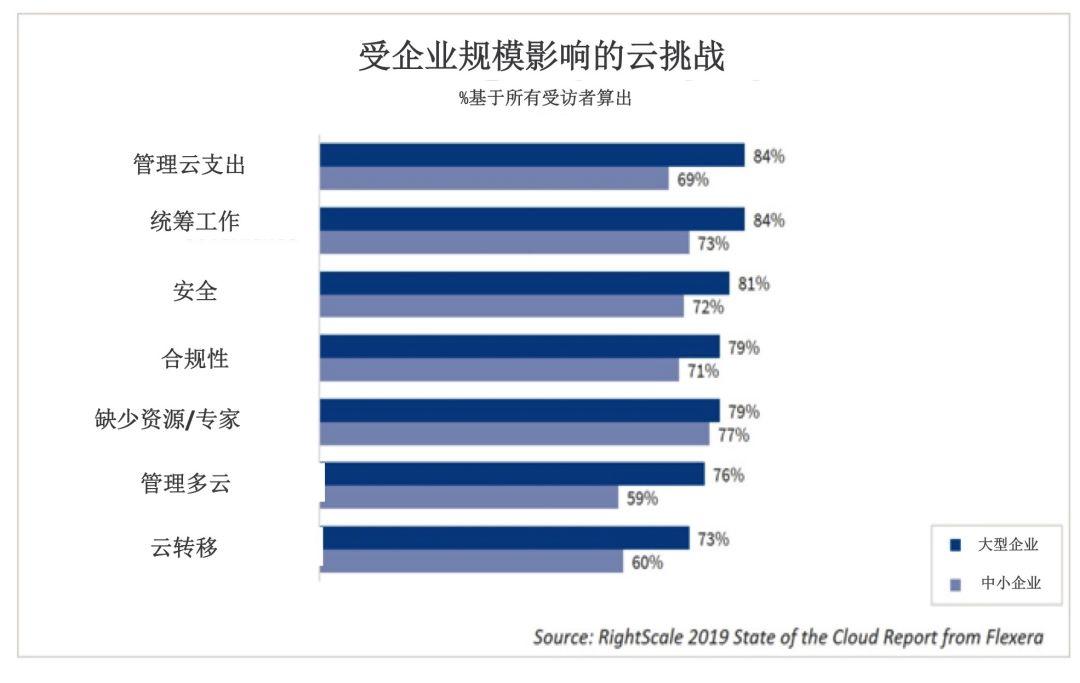
640?wx_fmt=png

总的来说，企业没有对云使用政策进行自动化，也低估了他们在这方面的开支，企业甚至没有大范围地使用折扣来降低成本。

与此同时，容器也被迅速采用。

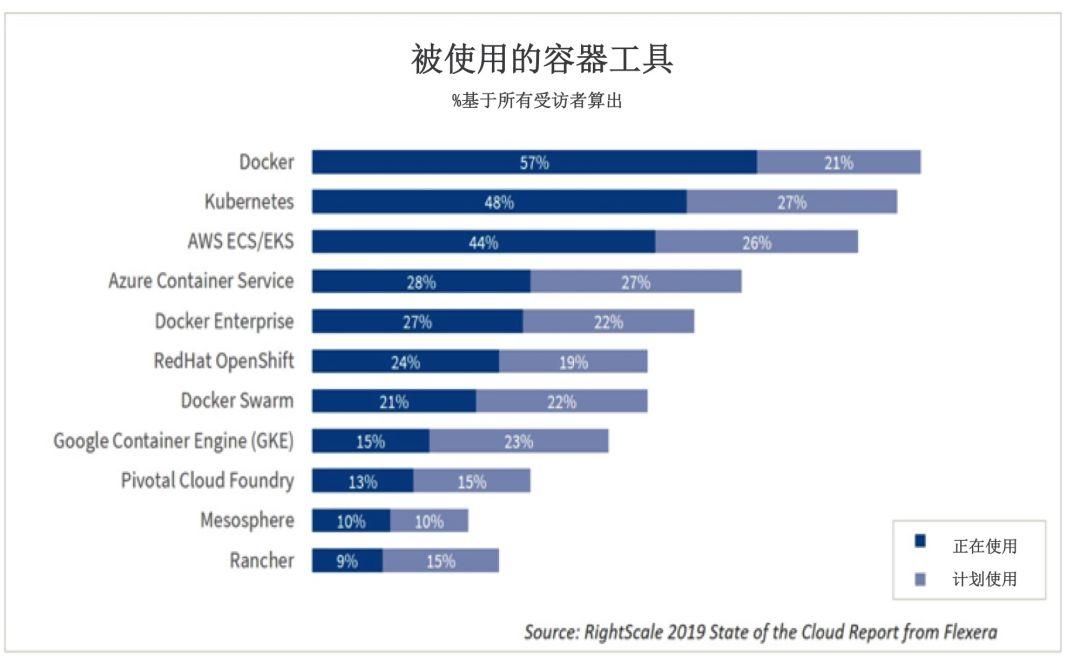
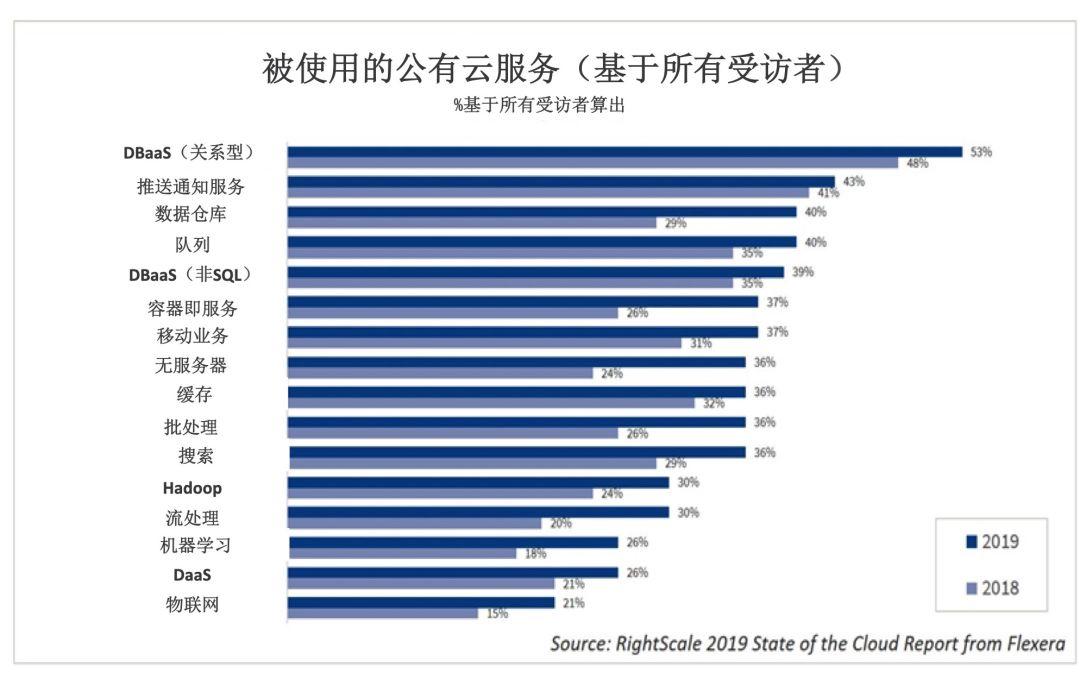
640?wx_fmt=png

增长最快的公有云服务是无服务器类型，但数据库作为服务工具已被广泛采用。

640?wx_fmt=png

福利

扫描添加小编微信，备注“姓名+公司职位”，加入【云计算学习交流群】，和志同道合的朋友们共同打卡学习！

640?wx_fmt=jpeg

推荐阅读：

喜欢就点击“在看”吧

本文涉及知识点

【数学线性代数】差分约束

P5960 【模板】差分约束

题目描述

给出一组包含 $m$ 个不等式，有 $n$ 个未知数的形如：

${xc1−xc′1≤y1xc2−xc′2≤y2⋯xcm−xc′m≤ym$

$\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases}$

⎩ ⎨ ⎧ x_{c_{1}} - x_{c_{1}^{'}} \leq y_{1} x_{c_{2}} - x_{c_{2}^{'}} \leq y_{2} \dots x_{c_{m}} - x_{c_{m}^{'}} \leq y_{m}

的不等式组，求任意一组满足这个不等式组的解。

输入格式

第一行为两个正整数 $n, m$ ，代表未知数的数量和不等式的数量。

接下来 $m$ 行，每行包含三个整数 $c, c^{'}, y$ ，代表一个不等式 $x_c-x_{c'}\leq y$ 。

输出格式

一行， $n$ 个数，表示 $x_1 , x_2 \cdots x_n$ 的一组可行解，如果有多组解，请输出任意一组，无解请输出 NO。

输入输出样例 #1

输入 #1

输出 #1

5 3 5

说明/提示

样例解释

${x1−x2≤3x2−x3≤−2x1−x3≤1$

$\begin{cases}x_1-x_2\leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases}$

⎩ ⎨ ⎧ x_{1} - x_{2} \leq 3 x_{2} - x_{3} \leq - 2 x_{1} - x_{3} \leq 1

一种可行的方法是 $x_1 = 5, x_2 = 3, x_3 = 5$ 。

${5−3=2≤33−5=−2≤−25−5=0≤1$

$\begin{cases}5-3 = 2\leq 3 \\ 3 - 5 = -2 \leq -2 \\ 5 - 5 = 0\leq 1 \end{cases}$

⎩ ⎨ ⎧ 5 - 3 = 2 \leq 3 3 - 5 = - 2 \leq - 2 5 - 5 = 0 \leq 1

数据范围

对于 $100\%$ 的数据， $1\leq n,m \leq 5\times 10^3$ ， $-10^4\leq y\leq 10^4$ ， $1\leq c,c'\leq n$ ， $\neq c'$ 。

评分策略

你的答案符合该不等式组即可得分，请确保你的答案中的数据在 int 范围内。

如果并没有答案，而你的程序给出了答案，SPJ 会给出 There is no answer, but you gave it，结果为 WA；
如果并没有答案，而你的程序输出了 NO，SPJ 会给出 No answer，结果为 AC；
如果存在答案，而你的答案错误，SPJ 会给出 Wrong answer，结果为 WA；
如果存在答案，且你的答案正确，SPJ 会给出 The answer is correct，结果为 AC。

图论差分约束

每个变量看成一个点，不等式看成边。增加一个超级源点src(0)，到各点的距离为0。src到节点1的距离为x1,src到节点2的距离为x2，x1 - x2<=3 $\iff$ x有权位3的边到x1。如果没有负环，最短距离就是一组解，则解各未知数增加任意数d，也是解。如果有负环，则无解。
贝尔曼-福特(Bellman-Ford)算法松弛N次，看和松弛N-1是否有区别，如果有区别则返回NO。否则各点最短距离。

代码

核心代码

#include 
#include 
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include 
#include 
#include
#include
#include

#include 
using namespace std;

template<class T1, class T2>
std::istream& operator >> (std::istream& in, pair<T1, T2>& pr) {
	in >> pr.first >> pr.second;
	return in;
}

template<class T1, class T2, class T3 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3>& t) {
	in >> get<0>(t) >> get<1>(t) >> get<2>(t);
	return in;
}

template<class T1, class T2, class T3, class T4 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3, T4>& t) {
	in >> get<0>(t) >> get<1>(t) >> get<2>(t) >> get<3>(t);
	return in;
}

template<class T = int>
vector<T> Read() {
	int n;
	scanf("%d", &n);
	vector<T> ret(n);
	for (int i = 0; i < n; i++) {
		cin >> ret[i];
	}
	return ret;
}

template<class T = int>
vector<T> Read(int n) {
	vector<T> ret(n);
	for (int i = 0; i < n; i++) {
		cin >> ret[i];
	}
	return ret;
}

template<int N = 1'000'000>
class COutBuff
{
public:
	COutBuff() {
		m_p = puffer;
	}
	template<class T>
	void write(T x) {
		int num[28], sp = 0;
		if (x < 0)
			*m_p++ = '-', x = -x;

		if (!x)
			*m_p++ = 48;

		while (x)
			num[++sp] = x % 10, x /= 10;

		while (sp)
			*m_p++ = num[sp--] + 48;
		AuotToFile();
	}
	void writestr(const char* sz) {
		strcpy(m_p, sz);
		m_p += strlen(sz);
		AuotToFile();
	}
	inline void write(char ch)
	{
		*m_p++ = ch;
		AuotToFile();
	}
	inline void ToFile() {
		fwrite(puffer, 1, m_p - puffer, stdout);
		m_p = puffer;
	}
	~COutBuff() {
		ToFile();
	}
private:
	inline void AuotToFile() {
		if (m_p - puffer > N - 100) {
			ToFile();
		}
	}
	char  puffer[N], * m_p;
};

template<int N = 1'000'000>
class CInBuff
{
public:
	inline CInBuff() {}
	inline CInBuff<N>& operator>>(char& ch) {
		FileToBuf();
		ch = *S++;
		return *this;
	}
	inline CInBuff<N>& operator>>(int& val) {
		FileToBuf();
		int x(0), f(0);
		while (!isdigit(*S))
			f |= (*S++ == '-');
		while (isdigit(*S))
			x = (x << 1) + (x << 3) + (*S++ ^ 48);
		val = f ? -x : x; S++;//忽略空格换行		
		return *this;
	}
	inline CInBuff& operator>>(long long& val) {
		FileToBuf();
		long long x(0); int f(0);
		while (!isdigit(*S))
			f |= (*S++ == '-');
		while (isdigit(*S))
			x = (x << 1) + (x << 3) + (*S++ ^ 48);
		val = f ? -x : x; S++;//忽略空格换行
		return *this;
	}
	template<class T1, class T2>
	inline CInBuff& operator>>(pair<T1, T2>& val) {
		*this >> val.first >> val.second;
		return *this;
	}
	template<class T1, class T2, class T3>
	inline CInBuff& operator>>(tuple<T1, T2, T3>& val) {
		*this >> get<0>(val) >> get<1>(val) >> get<2>(val);
		return *this;
	}
	template<class T1, class T2, class T3, class T4>
	inline CInBuff& operator>>(tuple<T1, T2, T3, T4>& val) {
		*this >> get<0>(val) >> get<1>(val) >> get<2>(val) >> get<3>(val);
		return *this;
	}
	template<class T = int>
	inline CInBuff& operator>>(vector<T>& val) {
		int n;
		*this >> n;
		val.resize(n);
		for (int i = 0; i < n; i++) {
			*this >> val[i];
		}
		return *this;
	}
	template<class T = int>
	vector<T> Read(int n) {
		vector<T> ret(n);
		for (int i = 0; i < n; i++) {
			*this >> ret[i];
		}
		return ret;
	}
	template<class T = int>
	vector<T> Read() {
		vector<T> ret;
		*this >> ret;
		return ret;
	}
private:
	inline void FileToBuf() {
		const int canRead = m_iWritePos - (S - buffer);
		if (canRead >= 100) { return; }
		if (m_bFinish) { return; }
		for (int i = 0; i < canRead; i++)
		{
			buffer[i] = S[i];//memcpy出错			
		}
		m_iWritePos = canRead;
		buffer[m_iWritePos] = 0;
		S = buffer;
		int readCnt = fread(buffer + m_iWritePos, 1, N - m_iWritePos, stdin);
		if (readCnt <= 0) { m_bFinish = true; return; }
		m_iWritePos += readCnt;
		buffer[m_iWritePos] = 0;
		S = buffer;
	}
	int m_iWritePos = 0; bool m_bFinish = false;
	char buffer[N + 10], * S = buffer;
};

template<class T = int, T iDef = INT_MAX / 2>
class CDisNegativeRing //贝尔曼-福特算法
{
public:
	bool Dis(int N, vector<tuple<int, int, int>> edgeFromToW, int start) {
		vector<vector<T>> diss(N + 1, vector<int>(N, iDef));
		diss[0][start] = 0;
		for (int t = 0; t < N; t++) {
			diss[t + 1] = diss[t];
			for (const auto& [u, v, w] : edgeFromToW) {
				diss[t + 1][v] = min(diss[t + 1][v], diss[t][u] + w);
			}
		}
		m_vDis = diss.back();
		for (int i = 0; i < N; i++) {
			if (diss[N][i] != diss[N - 1][i]) { return false; }
		}
		return true;
	}
	vector<T> m_vDis;
};
class Solution {
public:
	vector<int> Ans(int N, vector<tuple<int, int, int>> edge) {
		for (auto& [v, u, w] : edge) {
			swap(u, v);
		}
		for (int i = 1; i <= N; i++) {
			edge.emplace_back(0, i, 0);
		}
		CDisNegativeRing<> dis;
		if (!dis.Dis(N + 1, edge, 0)) { return {}; }

		return vector<int>(dis.m_vDis.begin() + 1, dis.m_vDis.end());
	}
};
int main() {
#ifdef _DEBUG
	freopen("a.in", "r", stdin);
#endif // DEBUG	
	ios::sync_with_stdio(0);
	int n, m; ;
	cin >> n >> m ;	
	auto edge = Read<tuple<int, int,int>>(m);
#ifdef _DEBUG		
	//printf("T=%lld,", T);
	//Out(ks, "ks=");
	//Out(edge, ",edge=");
	/*Out(edge, "edge=");
	Out(que, "que=");*/
#endif // DEBUG	
	auto res = Solution().Ans(n,edge);
	if (0 == res.size()) {
		cout << "NO";
	}
	for (const auto& i : res) {
		cout << i << " ";
	}
	return 0;
}

单元测试

	void Check(const vector<tuple<int, int, int>>& edge,const vector<int>& res) {
			for (const auto& [x1, x2, y] : edge) {
				Assert::IsTrue(res[x1 - 1] - res[x2 - 1] <= y);
			}
		}
		TEST_METHOD(TestMethod1)
		{
			vector<tuple<int, int, int>> edge = { {1,2,3},{2,3,-2},{1,3,1} };
			auto res = Solution().Ans(3,edge);
			Check(edge, res);
		}
		TEST_METHOD(TestMethod12)
		{
			vector<tuple<int, int, int>> edge = { {1,2,1} };
			auto res = Solution().Ans(2, edge);
			AssertEx({ 0,0 }, res);
		}
		TEST_METHOD(TestMethod13)
		{
			vector<tuple<int, int, int>> edge = { {1,2,-1} };
			auto res = Solution().Ans(2, edge);
			AssertEx({ -1,0 }, res);
		}
		TEST_METHOD(TestMethod14)
		{
			vector<tuple<int, int, int>> edge = { {1,2,-1},{2,3,-2},{3,1,-2} };
			auto res = Solution().Ans(4, edge);
			Assert::IsTrue(0 == res.size());
		}

扩展阅读

我想对大家说的话
工作中遇到的问题，可以按类别查阅鄙人的算法文章，请点击《算法与数据汇总》。
学习算法：按章节学习《喜缺全书算法册》，大量的题目和测试用例，打包下载。重视操作
有效学习：明确的目标及时的反馈拉伸区（难度合适）专注
闻缺陷则喜(喜缺)是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛
失败+反思=成功成功+反思=成功

视频课程

先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

测试环境

操作系统：win7 开发环境： VS2019 C++17
或者操作系统：win10 开发环境： VS2022 C++17
如无特殊说明，本算法用**C++**实现。

算法及C++答疑请加群

QQ群名片

工作量不断增加的微软Azure，正缩小与亚马逊AWS的差距

戳蓝字“CSDN云计算”关注我们哦！

都道业务提升坑大事儿多，但英特尔云方案却说“简单”

云有约 | 蚂蚁金服bPaaS究竟是什么？

再不编程就老了！05 后比特币专家准备赚个 134,000,000 元！

Pig变飞机？AI为什么这么蠢 | Adversarial Attack

互联网没有春天

麦克阿瑟奖得主Dawn Song：区块链能保密和保护隐私？图样图森破！

2019年最值得关注的五大微服务发展趋势

本文涉及知识点

P5960 【模板】差分约束

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

图论差分约束

代码

核心代码

单元测试

扩展阅读

视频课程

测试环境

评论记录：

戳蓝字“CSDN云计算”关注我们哦！

都道业务提升坑大事儿多，但英特尔云方案却说“简单”

云有约 | 蚂蚁金服bPaaS究竟是什么？

再不编程就老了！05 后比特币专家准备赚个 134,000,000 元！

Pig变飞机？AI为什么这么蠢 | Adversarial Attack

互联网没有春天

麦克阿瑟奖得主Dawn Song：区块链能保密和保护隐私？图样图森破！

2019年最值得关注的五大微服务发展趋势

本文涉及知识点

P5960 【模板】差分约束

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

图论 差分约束

代码

核心代码

单元测试

扩展阅读

视频课程

测试环境

评论记录：

图论差分约束