推荐|李笑来登顶 GitHub TOP 榜！币圈大佬要教程序员如何自学编程

640?wx_fmt=gif

640?wx_fmt=jpeg

作者 | 郭芮

出品 | CSDN（ID:CSDNnews）

币圈红人李笑来，何许人也？

——从英语老师、作家，到比特币首富、投资人，李笑来的身上有着众多广为人知的标签。因“录音门”事件让人哗然不已的他近来频频神隐，最近却又带着登顶 GitHub 的编程项目“杀”回了大众视野。

640?wx_fmt=png

“币圈首富”李笑来的传奇

新东方名师出身的李笑来，曾在接受央视采访时自曝“拥有六位数的比特币”，堪比“比特币首富”——而这一点，在当年《华尔街日报》的报道中得到了彻底的证实，也引起了币圈内关于“李笑来传奇”的热议。

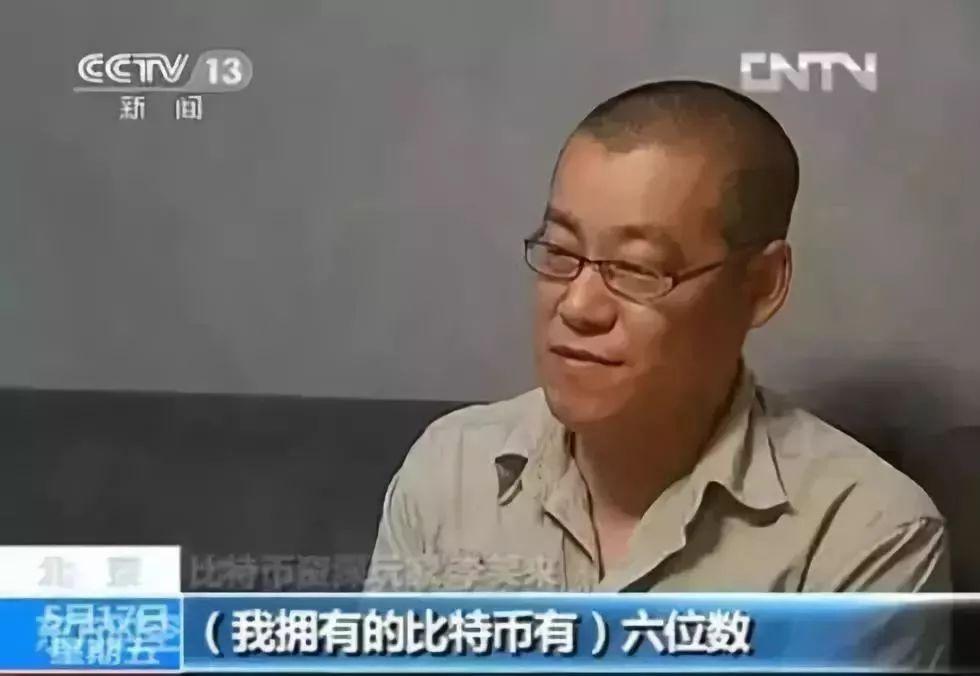
640?wx_fmt=jpeg

《华尔街日报》：“现年41岁的李笑来是中国持有比特币最多的人之一。”

在 2015 年底，罗振宇将李笑来《把时间当作朋友》的创意作为自己跨年演讲的主题，并把他的这本书拿到罗辑思维卖成了畅销书，为后者的名声远播加了一把大火。

640?wx_fmt=jpeg

但真正把他推到众矢之的的，则是去年那场让业界哗然的“录音门事件”。在被曝光的 50 多分钟录音中，不仅提到了“不要盲目相信价值投资”、“销售空气币”等敏感词汇，还将行业内的多数大佬都被数落了一番——也因此，李笑来被冠上了“割韭菜”的庄家之称。

舆论弥漫下，颇为尴尬的李笑来似乎逐渐变得低调了。而近日，时隔半年之久的他又带着一项登顶 GitHub 趋势榜的项目“杀”回了大众的视野。

640?wx_fmt=jpeg

640?wx_fmt=png

李笑来搞编程？

在李笑来之前的《韭菜的自我修养》一书中，提到了他与比特币的故事，并阐述了投资的第一原则是时刻保持学习。而在这个名为“自学是门手艺（the-craft-of-selfteaching）”的项目中，则以保持自学能力为主题。

640?wx_fmt=png

也许是李笑来的“光环加持”，截至目前项目上线 GitHub 还不足一周，就已经积累了 4693 个 Star、4273 个 Fork、281 个 commits 以及 58 位贡献者，可以说是“保送”GitHub 趋势榜 TOP 1 的席位了——直接火过了各大公司的众多开源项目。

640?wx_fmt=png

有趣的是，这本书就是一个以 Python 为主线的编程教学。

“完成这本书的内容，起码会习得一个新技能：编程。”通过纵读整个目录，除去一些心灵鸡汤式的“灵魂拷问”，确实也能看到“流程控制”、“函数”、“字符串”、“数据容器”等基础内容。

640?wx_fmt=png

除此之外，在结尾部分还附上了 Python 必读书籍、全栈工程师路径图等硬核内容（后者可移步CSDN此前发布的《开发者如何实现技能升级、薪资翻番？| 附终极学习路线图》一文，了解更多详情）。

640?wx_fmt=png

Python 必读书籍

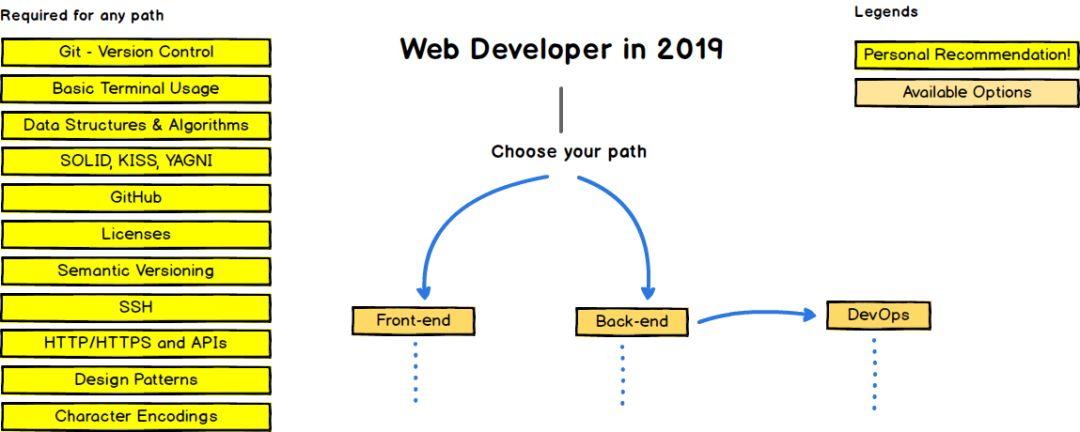
640?wx_fmt=png

前端学习路线图

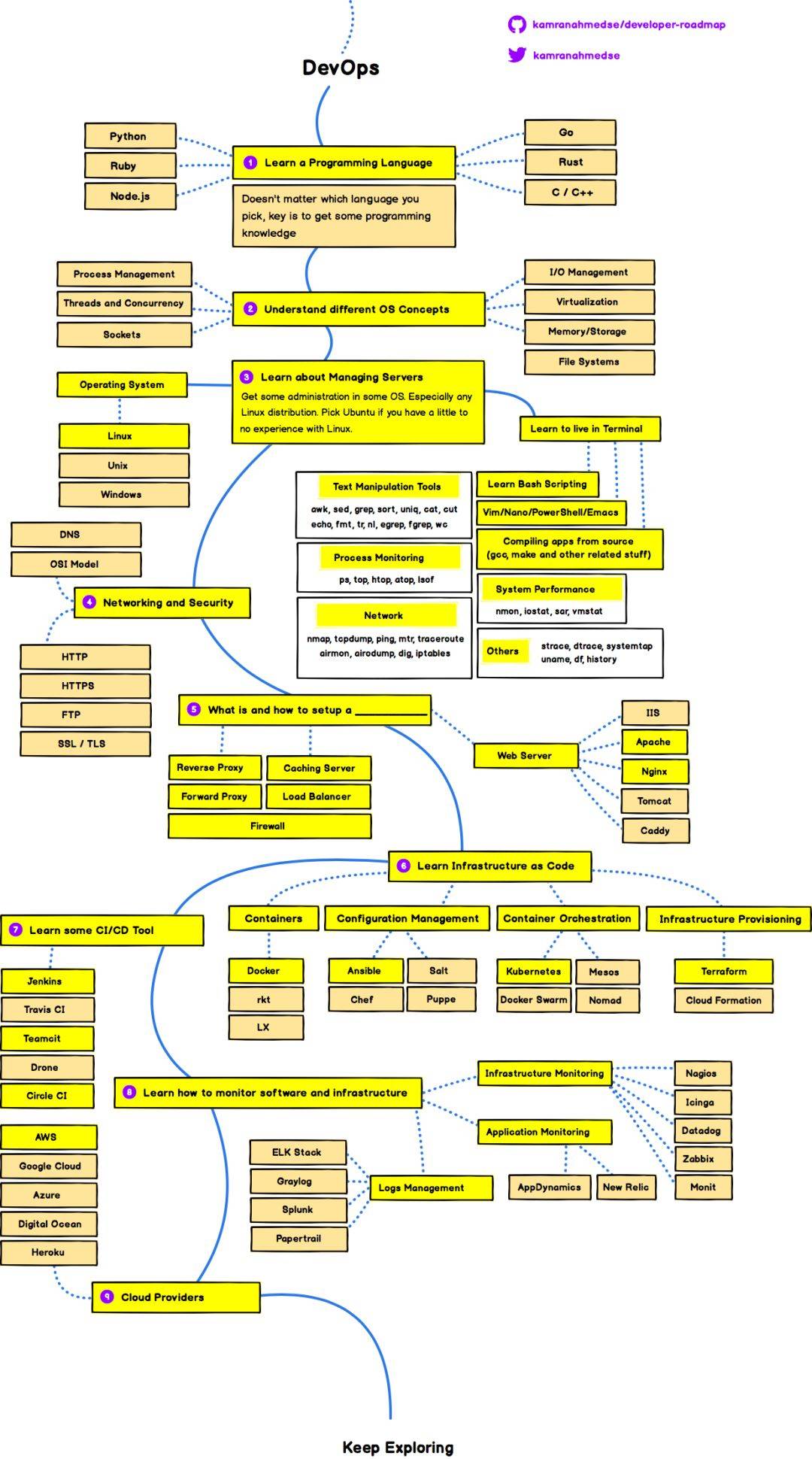
640?wx_fmt=png

后端学习路线图

640?wx_fmt=png

DevOps学习路线图

在最后，送上了满满干货的李笑来感叹，“这完全就是一场闯关游戏。”

640?wx_fmt=png

开发者怎么看？

“这些年来我写的书，都是关于学习的。无论是《把时间当作朋友》，还是《通往财富自由之路》，甚至《韭菜的自我修养》，背后都是同样的目标：学习、进步——甚至进化。”

以“教书育人”为己任的李笑来，此番开源自己的新书，也算是造福业界了。但是纵观网上的热议，却仍是褒贬不一。

有认可其开源价值的：

@太阳上面有新事_ ：虽然李笑来在币圈割了不少韭菜，不过他的书还是值得一看的。勿因人废言！

@濃姫：终于知道开源的书有多好了，可以pull request，还可以随时执行代码——推荐李笑来新书。

@jasonGsen：看了李笑来老师的 GitHub，里面关于真正则表达式的解释简直神了，当初如果老师这么和我说，我早就会了。

但更多的还是质疑这是否又是新一轮割韭菜的招数？

@majirefy：珍爱生命，远离编程；如果实在没法远离编程，那就珍爱生命，远离这货。

@皮卡卡卡丘：挺好的，fork 和 star 这个项目的 git 账号全爬下来，作为避险指南。

@滑稽势力：就是网上随处可见的Python入门教程里面搅和了缓解中产焦虑的鸡汤。

@瞄星阿福：满满的鸡汤，一些方法论，还有一些入门知识。这本书想学Python是不可能的，就是了解一下 Github 和 Jupyter Notebook。

@溯垚：李老师，上次被割后，刚撒上新韭的籽，要不要再呵护一下？

所以说，李老师想要撕掉“庄家”的标签，挽救“为人师表”的形象，看样子仍然任重而道远啊。

感兴趣的同学也可以去他的 GitHub 主页围观之：

https://github.com/selfteaching/the-craft-of-selfteaching。

#欢迎来留言#

你对李笑来登顶 GitHub有什么看法呢？

【offer去哪了】我一连面试了十个Java岗，统统石沉大海！

https://edu.csdn.net/topic/python115?utm_source=cxrs_bw

640?wx_fmt=png

640?wx_fmt=gif

热文 推荐

☞硬核接亲！程序员被新娘要求现场写代码，结果万万没想到……

☞高级撩妹！如何一键定时给妹子发表白微信？

☞程序员版的《小王子》，过于真实！

☞小米“祭出” AIoT 神器！| 技术头条

☞95 后天才读数千页 Intel CPU 手册发现危及全球重大漏洞！

☞工作量不断增加的微软Azure，正缩小与亚马逊AWS的差距

☞理工男的网红生意, 6000万月活50万条日更的背后, 内容链还能这样操作？

☞68款大规模机器学习数据集，涵盖CV、语音、NLP | 十年资源集

☞那些简历造假拿 Offer 的程序员，后来都怎样了？

System.out.println("点个在看吧！");
console.log("点个在看吧！");
print("点个在看吧！");
printf("点个在看吧！\n");
cout << "点个在看吧！" << endl;
Console.WriteLine("点个在看吧！");
Response.Write("点个在看吧！");
alert("点个在看吧！")
echo "点个在看吧！"

640?wx_fmt=png 喜欢就点击“在看”吧！

程序人生

微信公众号

笑谈开发轶事，品味程序人生。

本文涉及知识点

【数学线性代数】差分约束

P4878 [USACO05DEC] Layout G

题目描述

正如其他物种一样，奶牛们也喜欢在排队打饭时与它们的朋友挨在一起。FJ 有编号为 $1\dots N$ 的 $N$ 头奶牛 $(2\le N\le 1000)$ 。开始时，奶牛们按照编号顺序来排队。奶牛们很笨拙，因此可能有多头奶牛在同一位置上。

有些奶牛是好基友，它们希望彼此之间的距离小于等于某个数。有些奶牛是情敌，它们希望彼此之间的距离大于等于某个数。

给出 $M_L$ 对好基友的编号，以及它们希望彼此之间的距离小于等于多少；又给出 $M_D$ 对情敌的编号，以及它们希望彼此之间的距离大于等于多少 $(1\le M_L,$ $M_D\le 10^4)$ 。

请计算：如果满足上述所有条件， $1$ 号奶牛和 $N$ 号奶牛之间的距离最大为多少。

输入格式

第一行：三个整数 $N, M_L, M_D$ ，用空格分隔。

第 $2\dots M_L+1$ 行：每行三个整数 $A, B, D$ ，用空格分隔，表示 $A$ 号奶牛与 $B$ 号奶牛之间的距离须 $\le D$ 。保证 $1\le A1≤A<B≤N,$

第 $M_L+2\dots M_L+M_D+1$ 行：每行三个整数 $A, B, D$ ，用空格分隔，表示 $A$ 号奶牛与 $B$ 号奶牛之间的距离须 $\ge D$ 。保证 $1\le A1≤A<B≤N,$

输出格式

一行，一个整数。如果没有合法方案，输出 -1. 如果有合法方案，但 $1$ 号奶牛可以与 $N$ 号奶牛相距无穷远，输出 -2. 否则，输出 $1$ 号奶牛与 $N$ 号奶牛间的最大距离。

输入输出样例 #1

输入 #1

输出 #1

差分约束

注意：本题规定按编号排队。故只需考虑B-A <= D，不需要考虑A-B <=D。
差分系统的边：
一，好友。B - A <= D。
二，仇敌。B - A >= D 就A-B <= -D
三，必须按规定编号排队，故必须：i - (i+1) <= -1
如果存在负环，返回-1。如果1不是N的直接或间接前置节点，则返回-2。否则返回dis[N]-dis[1]。
题外话：如果N不是1的直接或间接前置节点，dis[N]-dis[1]可以是无穷小。
边权在正负1e6之间，边数在1000以内。在正数范围内。小于 a=INT_MAX/2。

方式一

1增加指向所有其它点的边，权重2a， INF=LLONGMAX/2。由于有负权边，所以增加的边不能是a。
这样点1和所有点都连通，直接以1为起点：判断负环、判断1和N是否连通、1到N的距离。
如果dis[N] >= a，说明1和N并不连通。

方式二

增加0到各点的边，权重0。以0为源点判断是否有负环。以1为起点判断连通性，并求dis[N]。

代码

核心代码

#include 
#include 
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include 
#include 
#include
#include
#include

#include 
using namespace std;

template<class T1, class T2>
std::istream& operator >> (std::istream& in, pair<T1, T2>& pr) {
	in >> pr.first >> pr.second;
	return in;
}

template<class T1, class T2, class T3 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3>& t) {
	in >> get<0>(t) >> get<1>(t) >> get<2>(t);
	return in;
}

template<class T1, class T2, class T3, class T4 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3, T4>& t) {
	in >> get<0>(t) >> get<1>(t) >> get<2>(t) >> get<3>(t);
	return in;
}

template<class T = int>
vector<T> Read() {
	int n;
	scanf("%d", &n);
	vector<T> ret(n);
	for (int i = 0; i < n; i++) {
		cin >> ret[i];
	}
	return ret;
}

template<class T = int>
vector<T> Read(int n) {
	vector<T> ret(n);
	for (int i = 0; i < n; i++) {
		cin >> ret[i];
	}
	return ret;
}

template<int N = 1'000'000>
class COutBuff
{
public:
	COutBuff() {
		m_p = puffer;
	}
	template<class T>
	void write(T x) {
		int num[28], sp = 0;
		if (x < 0)
			*m_p++ = '-', x = -x;

		if (!x)
			*m_p++ = 48;

		while (x)
			num[++sp] = x % 10, x /= 10;

		while (sp)
			*m_p++ = num[sp--] + 48;
		AuotToFile();
	}
	void writestr(const char* sz) {
		strcpy(m_p, sz);
		m_p += strlen(sz);
		AuotToFile();
	}
	inline void write(char ch)
	{
		*m_p++ = ch;
		AuotToFile();
	}
	inline void ToFile() {
		fwrite(puffer, 1, m_p - puffer, stdout);
		m_p = puffer;
	}
	~COutBuff() {
		ToFile();
	}
private:
	inline void AuotToFile() {
		if (m_p - puffer > N - 100) {
			ToFile();
		}
	}
	char  puffer[N], * m_p;
};

template<int N = 1'000'000>
class CInBuff
{
public:
	inline CInBuff() {}
	inline CInBuff<N>& operator>>(char& ch) {
		FileToBuf();
		ch = *S++;
		return *this;
	}
	inline CInBuff<N>& operator>>(int& val) {
		FileToBuf();
		int x(0), f(0);
		while (!isdigit(*S))
			f |= (*S++ == '-');
		while (isdigit(*S))
			x = (x << 1) + (x << 3) + (*S++ ^ 48);
		val = f ? -x : x; S++;//忽略空格换行		
		return *this;
	}
	inline CInBuff& operator>>(long long& val) {
		FileToBuf();
		long long x(0); int f(0);
		while (!isdigit(*S))
			f |= (*S++ == '-');
		while (isdigit(*S))
			x = (x << 1) + (x << 3) + (*S++ ^ 48);
		val = f ? -x : x; S++;//忽略空格换行
		return *this;
	}
	template<class T1, class T2>
	inline CInBuff& operator>>(pair<T1, T2>& val) {
		*this >> val.first >> val.second;
		return *this;
	}
	template<class T1, class T2, class T3>
	inline CInBuff& operator>>(tuple<T1, T2, T3>& val) {
		*this >> get<0>(val) >> get<1>(val) >> get<2>(val);
		return *this;
	}
	template<class T1, class T2, class T3, class T4>
	inline CInBuff& operator>>(tuple<T1, T2, T3, T4>& val) {
		*this >> get<0>(val) >> get<1>(val) >> get<2>(val) >> get<3>(val);
		return *this;
	}
	template<class T = int>
	inline CInBuff& operator>>(vector<T>& val) {
		int n;
		*this >> n;
		val.resize(n);
		for (int i = 0; i < n; i++) {
			*this >> val[i];
		}
		return *this;
	}
	template<class T = int>
	vector<T> Read(int n) {
		vector<T> ret(n);
		for (int i = 0; i < n; i++) {
			*this >> ret[i];
		}
		return ret;
	}
	template<class T = int>
	vector<T> Read() {
		vector<T> ret;
		*this >> ret;
		return ret;
	}
private:
	inline void FileToBuf() {
		const int canRead = m_iWritePos - (S - buffer);
		if (canRead >= 100) { return; }
		if (m_bFinish) { return; }
		for (int i = 0; i < canRead; i++)
		{
			buffer[i] = S[i];//memcpy出错			
		}
		m_iWritePos = canRead;
		buffer[m_iWritePos] = 0;
		S = buffer;
		int readCnt = fread(buffer + m_iWritePos, 1, N - m_iWritePos, stdin);
		if (readCnt <= 0) { m_bFinish = true; return; }
		m_iWritePos += readCnt;
		buffer[m_iWritePos] = 0;
		S = buffer;
	}
	int m_iWritePos = 0; bool m_bFinish = false;
	char buffer[N + 10], * S = buffer;
};

template<class T = int, T iDef = INT_MAX / 2>
class CDisNegativeRing //贝尔曼-福特算法
{
public:
	bool Dis(int N, vector<tuple<int, int, int>> edgeFromToW, int start) {
		vector<vector<T>> diss(N + 1, vector<T>(N, iDef));
		diss[0][start] = 0;
		for (int t = 0; t < N; t++) {
			diss[t + 1] = diss[t];
			for (const auto& [u, v, w] : edgeFromToW) {
				diss[t + 1][v] = min(diss[t + 1][v], diss[t][u] + w);
			}
		}
		m_vDis = diss.back();
		for (int i = 0; i < N; i++) {
			if (diss[N][i] != diss[N - 1][i]) { return false; }
		}
		return true;
	}
	vector<T> m_vDis;
};

class Solution {
public:
	int Ans(int N, const vector<tuple<int, int, int>> edge1, const vector<tuple<int, int, int>> edge2) {
		vector<tuple<int, int, int>> edge;
		for (auto& [a, b, d] : edge1) {
			edge.emplace_back(a, b, d);
		}
		for (auto& [a, b, d] : edge2) {
			edge.emplace_back(b, a, -d);
		}
		for (int i = 1; i <= N; i++) {
			edge.emplace_back(0, i, INT_MAX / 2);
			edge.emplace_back(i, 0, INT_MAX / 2);
		}
		for (int i = 1; i < N; i++) {
			edge.emplace_back(i + 1, i, -1);
		}
		CDisNegativeRing<long long, LLONG_MAX / 2> dis;
		if (!dis.Dis(N + 1, edge, 1)) { return -1; }
		if (dis.m_vDis[N] > INT_MAX / 2) { return -2; }
		return dis.m_vDis[N] - dis.m_vDis[1];
	}
};

int main() {
#ifdef _DEBUG
	freopen("a.in", "r", stdin);
#endif // DEBUG	
	ios::sync_with_stdio(0);
	int n, m1,m2 ;
	cin >> n >> m1 >> m2 ;	
	auto edge1 = Read<tuple<int, int,int>>(m1);
	auto edge2 = Read<tuple<int, int, int>>(m2);
#ifdef _DEBUG		
	printf("n=%d,", n);
	//Out(ks, "ks=");
	Out(edge1, ",edge1=");
	Out(edge2, ",edge2=");
	/*Out(que, "que=");*/
#endif // DEBUG	
	auto res = Solution().Ans(n,edge1,edge2);
	cout << res;
	return 0;
}

单元测试

int n;
		vector<tuple<int, int, int>> edge1, edge2;
		TEST_METHOD(TestMethod1)
		{
			n = 4,  edge1 = { {1,3,10},{2,4,20} }, edge2 = { {2,3,3} };	
			auto res = Solution().Ans(n,edge1,edge2);
			AssertEx(27, res);
		}
		TEST_METHOD(TestMethod2)
		{
			n = 3, edge1 = { {1,3,1} }, edge2 = { {1,2,1},{2,3,1} };	
			auto res = Solution().Ans(n, edge1, edge2);
			AssertEx(-1, res);
		}
		TEST_METHOD(TestMethod3)
		{
			n = 3, edge1 = { {1,2,1} }, edge2 = { };
			auto res = Solution().Ans(n, edge1, edge2);
			AssertEx(-2, res);
		}
		TEST_METHOD(TestMethod4)
		{
			n = 4, edge1 = { {1,4,10} }, edge2 = { {2,3,20} };
			auto res = Solution().Ans(n, edge1, edge2);
			AssertEx(-1, res);
		}

扩展阅读

我想对大家说的话
工作中遇到的问题，可以按类别查阅鄙人的算法文章，请点击《算法与数据汇总》。
学习算法：按章节学习《喜缺全书算法册》，大量的题目和测试用例，打包下载。重视操作
有效学习：明确的目标及时的反馈拉伸区（难度合适）专注
闻缺陷则喜(喜缺)是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛
失败+反思=成功成功+反思=成功

视频课程

先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

测试环境

操作系统：win7 开发环境： VS2019 C++17
或者操作系统：win10 开发环境： VS2022 C++17
如无特殊说明，本算法用**C++**实现。

算法及C++答疑请加群

QQ群名片

本文涉及知识点

P4878 [USACO05DEC] Layout G

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

差分约束

方式一

方式二

代码

核心代码

单元测试

扩展阅读

视频课程

测试环境

评论记录：