推荐|2019，国产手机生死存亡的一年

640?wx_fmt=gif

640?wx_fmt=jpeg

作者 | 方文

本文经授权转自猎云网（ID: ilieyun）

责编 | 屠敏

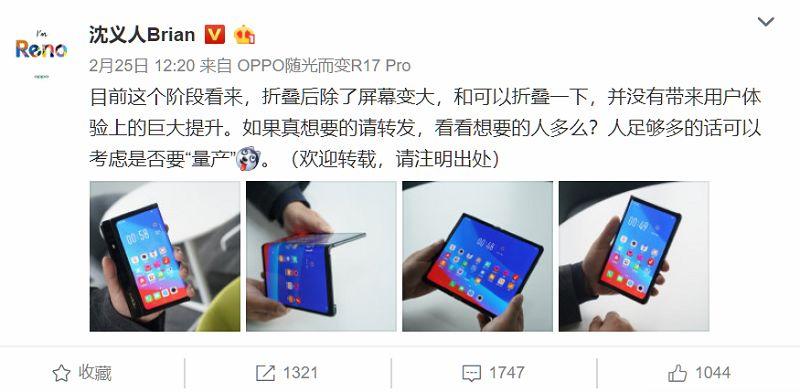
OPPO副总裁沈义人给现在火热的5G和折叠屏泼了两盆冷水。

“目前这个阶段看来，折叠后除了屏幕变大，和可以折叠一下，并没有带来用户体验上的巨大提升。”

“普通用户这两年没必要特别期待5G手机，受网络、消费内容、终端售价多方面影响，5G手机短期内不会大范围普及。现在的5G手机是供厂商展示研发能力、为开发者搭建应用环境和少部分数码发烧用户尝鲜。”

640?wx_fmt=png

不止沈义人一个，尽管在5G这样的大趋势，以及折叠屏如此受热捧的情况下，对新技术在短时期带来的效益存在疑问的大佬不在少数。

沈义人说的是事实，按照运营商的规划，5G手机开始应用最早也在2020年，而折叠屏这项技术自身也需要一段时间进行完善，再加上5G和折叠屏带来的互联网内容生态的变化，大的4G换机潮至少是2年以后的事情了。这两年内，4G手机的巨大存量用户依然会是主流，手机厂商们胶着的贴身战还在可量产的消费机而非概念机市场。

然而，即使是纯投入不见回报，想要在5G和折叠屏的争夺中领先，最好的布局时间就是现在。不同手机厂商对自身定位和技术带来巨变的判断，导致国产手机厂商在这一波浪潮中逐渐的分为两派：一派是坚定押注未来的技术派，一派是着眼现在抢占市场的制造派。

2019年，国产手机厂商的竞争和之前不同。如果说之前还是停留在市场份额的争夺上，还在依靠全面屏、拍照、手机外形和颜色作为手机卖点的话，在5G和折叠屏这个大的技术变革面前，能否提前做好布局，能否为自己争取到更多的资本，都关乎到下一个十年的生死存亡。大厂可能没落，小品牌有机会崛起，一切可能是一个新的开始。

640?wx_fmt=png

技术派和制造派的分化

谁是技术派，谁是制造派，和各家手机厂商的自身的定位和判断有关，也很大程度上和一直以来的技术储备和发展路线有关。

何为技术派？技术派指的是，押注未来趋势技术，不求短期回报，期许将来凭借技术的领先占领市场高地。

对于智能手机来说，这类的技术主要是构成手机和通信的底层能力，包括下一代通信技术5G、以折叠屏为希望的新一代屏幕技术、以AI为代表的新的操作系统和人机交互方式以及手机核心部件芯片。5G、屏幕、AI分别代表了通信技术的迁移，智能终端设备的迁移和消费者使用手机习惯的更替。

5G通信是手机基本通信能力，折叠屏则可能是下一代终端屏幕的希望。除此之外，下一代终端设备，是否还是Android、iOS也是未知。从PC到移动端，就经历了Windows到Android、iOS的转变。

一个有意思的消息是，微软正在开发轻量级的操作系统Windows lite以适应在折叠屏上的应用。折叠屏手机属于平板和手机中间状态，微软是否可以借助此契机卷土重来？

华为余承东近期也曾表示过，如果迫不得已，将放弃Windows和Android系统转向内部解决方案（内部有替代这两大生态的自主系统）。而余承东同时也展望了基于AR眼镜的10英寸到20英寸的手机屏幕。

一方面，华为有能力在自家的手机上采用自主的系统，另外一方面，不论是折叠屏，还是AR形态，下一代终端的操作方式极有可能发生大的变化，届时是Windows这样的大屏的操作系统重新适配手机，还是类似华为YOYO生命体这样的新型的以语音和AI为载体的操作系统会成为主流？

何为制造派？制造派指的是，充分发挥自身产品的市场定位，通过对手机外观、颜色和其他功能的打磨，对现有产品的设计和制造工艺进行改进，给消费者提供更细腻的使用体验。应用层的技术包括电池续航能力、充电方式和速度、以Face ID和屏下解锁为代表的安全能力、拍照能力等。

这是近几年来国产手机争夺的方向，也是各家争相的新机卖点。比如说电池的续航能力、无线和快充技术等，这些技术更多的是和手机的实现功能相关。小米MIX3的发布会上，雷军特地和华为的拍照能力进行了比对来凸显实力；vivo的光电屏幕指纹技术在去年赚足了眼球；OPPO的快充技术一直是核心卖点；锤子手机人性化的设计；魅族note9主打的是千元机中工艺的考究。

在过去的一年，智能手机市场整体下滑，竞争更加的激烈，各家手机厂商就是在不断地加强这些见效更明显的应用层面的技术，甚至机身颜色，当然这也是很多消费者的换机参考因素。

小米的技术储备一直以来都是比较薄弱的，根据小米2018年中报，上半年集团技术研发投入仅25亿，虽然有大幅的增加，但是依然远远落后于竞争对手华为。小米在技术方面长期的不足，在2月26日，小米组织架构调整更是成立了技术委员会。即使是制造派，也在更多地加强技术含量，这对于提升手机的使用体验来说是非常重要的。

640?wx_fmt=png

国产手机迎来最艰难的一年

2019年会是国产手机最艰难的一年。处在5G、折叠屏这样一个技术转换的过渡时代，押注未来还是着眼现在，都是非常吃力的一件事，对厂商来说确实意义深远。

IDC最新的数据显示，全球手机市场2018年继续下滑4.1%，国产手机虽然在全球市场份额增长迅速，华为第三季度曾超过苹果成为全球第二大出货量手机品牌。但是在大环境是负增长的情况下，国产手机面临的是竞争更加的激烈，而且同质化严重。

在2018年，中国智能手机品牌从原来最繁荣时的6000多个品牌，仅存现在不足几十个，并在国内形成华米OV格局，老罗的锤子科技在2019年终于情怀不敌现实的残酷，魅族也陷入困局。

手机厂商在2018年，在手机上的创新更多的是在屏幕、相机、颜色革命等外围，可以认为是边角料的创新。

640?wx_fmt=jpeg

新年伊始，各家厂商就频发新机。

2月20日，小米9发布；

2月28日三星S10发布；

3月1日，vivo全新子品牌iQOO发布；

3月7日，魅族note9发布；

华为Pro30将在3月底发布；

OPPO全新系列Reno将在4月发布。

国产手机品牌在不断地寻找更加适合不同人群定位的产品。vivo成立独立子品牌IQOO，小米独立出红米，OPPO发布新系列RENO。

但是我们看到，国产手机品牌，或者即使是三星，都不再推出新的酷炫的功能作为卖点，更多的去主打性价比，更多的是加强上一代产品的工艺。当小米9喊出“好看又能打”这样的一个口号的时候，小米手机在4G时代的创新就基本宣告停止了，性价比和手机使用体验磨合好就可以了，更多的酷炫的，先进的功能和使用体验，将会寄托在5G和折叠屏时代。

但是到了2019年，智能手机的环境就变得不同了，5G和折叠屏技术，都将在2年内落地，这是两个将引领下一代终端设备的技术，手机厂商能否抓住这两个技术红利，以及接下来的换机红利，将会影响各家在未来的中国乃至全球的市场。

2月底的MWC，华为、小米、一加等5G手机亮相，华为的折叠屏手机HUAWEI Mate X售价17500元更是引起轰动。各手机厂商对5G和折叠屏的态度不尽相同，华为和三星针锋相对，要在5G、折叠屏时代，一争高下，而一加、OV对折叠屏冷淡。

一加的刘作虎在采访中明确表示暂时不做全面屏，传OPPO原先计划在MWC2019上展示的折叠屏跳票，在华为展出mateX之后的第二天，沈义人在微博上的晒出样机。Vivo新的子品牌iQOO正式发布前，因为一张疑似流出的渲染图，被误以为是折叠屏手机。

从真机到渲染图，国产手机厂商在折叠屏的研发上，虽然都没量产，但是差距还是有的。

640?wx_fmt=png

谁会赢下手机新时代

技术派和制造派，就一定谁输谁赢吗？不完全是。

在《创新者的窘境》中作者描述过这种现象，如果新事物是一种延续性的创新，那原先具有市场和技术领先优势的企业，通过改进技术和工艺，在新的市场中将继续领先。但是如果出现的是破坏性的创新，那么原先具有市场和技术领先优势的公司，即使是已经发觉了市场的变化，也会遇到创新者的窘境，最终被新的企业超越。

那按照这种情况，5G和折叠屏，是不是破坏性的技术呢？

5G不是。5G是延续性技术的更新，只会强者更强。华为在5G的优势使得自己在通信产业链条中的话语权更强，对于小米和OV等厂商，5G的到来和4G的到来，没有什么区别。

折叠屏是破坏性技术吗？可能是的，折叠屏幕代表的是下一代屏幕。我们看到，现在很多手机厂商推出的是使手机屏幕如何变大，如何变成平板，但折叠屏的意义远不止于此。柔性屏的技术，带来的是屏幕的革命，而不是手机的革命。

比如，把手机变成平板，是现在各个手机厂商的思路，但是如果把watch变成手机，又是另外的一种终端使用体验。折叠屏将设备从小变大的意义，远不如将设备从大变小更加重要。

柔性屏技术的逐渐成熟，带来的是消费者屏幕使用习惯的大改变。而在初期，柔性屏的技术和体验，却可能在很长的一段时间内做的甚至不如原先的手机屏幕，当前各家发布的折叠屏样机、工程机，可以说是非常的丑陋，手机设计和制造的想象力还没有打开。这是典型的破坏性创新的特质。

技术派路线的手机厂商，对整个产业链比如成本、核心零部件供应等会有很强的把控能力。以5G通信专利为例，华为在5G上的专利持有，每一部手机的出厂成本就会比原先少一笔专利费，而同时，全球每生产一部5G手机，就会给华为交一笔专利费，两倍的专利使用费，会使得华为在手机的成本上就领先其他厂商，更不必说芯片、操作系统等方面的优势。

但是对于手机厂商，并非没有掌握核心科技就会在下一个时代消亡。5G普及后，即使折叠屏成为下一代主流，这两个公用的能力反而不会成为诸如小米、OV的掣肘。小米、OV等，同样都是采用国际通用的5G标准，而折叠屏、芯片等，同样也是向几家供应商采购。对于这些厂商来说，在市场立足，给消费者提供选择自己的理由是什么？就是其擅长的工艺和设计、拍照等方面的能力。

在一定程度上，乔布斯开创的这个iPhone时代就是一个制造派打败技术派的典例。世界上第一款智能手机是IBM公司1993年推出的Simon，它也是世界上第一款使用触摸屏的智能手机。而iPhone能赢得消费者青睐凭借的是自身设计的调性和近乎苛刻的工艺。

5G确实来了，新的终端屏幕也即将交替。对于OPPO、vivo、一加、魅族等，对于华为、小米，两个阵营的手机厂商采用不同的策略应对，都是“因地制宜”只不过今天种下什么种子，明天收获什么果实。

折叠屏最大的问题是技术？造价？都不是，最大的不确定性来自于市场接受度。苹果仅有几款机型，绝不会贸然推出折叠屏，苹果采用的策略大概率是技术跟进，但是不推新机。华为三星在安卓第一的争夺上，就算赔本也会不断的推出少量新机，当然，折叠屏高昂的造价，只适合做高端机。

OPPO、vivo最好的策略就是默默关注，即使是折叠屏开始流行起来，成熟的屏幕供应商，再加上设计和制造工艺的跟进，也并不会被大幅甩开。Surface的成功，Windows操作系统的优势，微软也可能成折叠屏设备领域最大的黑马。

2019年对国产手机厂商来说将是最艰难的一年，一方面要5G和折叠屏时代到来前，要提早做好布局，另一方面，又要保持住现有的市场份额，才不会在下一个时代到来前就被淘汰。

为什么Python成为第一编程语言？

https://edu.csdn.net/topic/python115?utm_source=cxrs_bw

640?wx_fmt=png

640?wx_fmt=gif

热文 推荐

☞李笑来登顶 GitHub TOP 榜！币圈大佬要教程序员如何自学编程

☞硬核接亲！程序员被新娘要求现场写代码，结果万万没想到……

☞前阿里 P9 级员工称离婚是模拟测试，已回滚复婚！

☞2019，国产手机生死存亡的一年

☞18 岁少年盗取价值 90 万元的萌乃币, 交易所被迫关停！

☞做了四年以太坊核心开发者, 以太坊升级了, 我也该离开了……

☞女生适合做程序员吗？

☞Google首页玩起小游戏，AI作曲让你变身巴赫

☞杨超越第一，Python第二！

System.out.println("点个在看吧！");
console.log("点个在看吧！");
print("点个在看吧！");
printf("点个在看吧！\n");
cout << "点个在看吧！" << endl;
Console.WriteLine("点个在看吧！");
Response.Write("点个在看吧！");
alert("点个在看吧！")
echo "点个在看吧！"

640?wx_fmt=png 喜欢就点击“在看”吧！

程序人生

微信公众号

笑谈开发轶事，品味程序人生。

本文涉及知识点

【数学线性代数】差分约束

P5590 赛车游戏

题目描述

R 君和小伙伴打算一起玩赛车。但他们被老司机 mocania 骗去了秋名山。

秋名山上有 $n$ 个点和 $m$ 条边，R 君和他的小伙伴要从点 $1$ 出发开往点 $n$ ，每条边都有一个初始的方向。老司机 mocania 拿到了秋名山的地图但却不知道每条路有多长。显然，为了赛车游戏的公平，每条 $1$ 到 $n$ 的路径应当是等长的。mocania 想，我就随便给边标上一个 $1...9$ 的长度，反正傻傻的 R 君也看不出来。

可 mocania 的数学不大好，不知道怎么给边标长度，只能跑来请教你这个 OI 高手了。

输入格式

第一行两个整数 $n, m$ 。

接下来 $m$ 行，每行两个整数 $u, v$ ，表示一条从 $u$ 到 $v$ 的有向边。

输出格式

如果无解或者不存在 $1$ 到 $n$ 的路径直接输出一个 $- 1$ 。

如果有解第一行输出两个数 $n, m$ ，和输入文件中给出的相同。

接下来 $m$ 行，每行三个整数 $u, v, w$ ，表示把从 $u$ 到 $v$ 的路径的长度设置为 $w$ ，其中 $w$ 是一个 $1\sim 9$ 的整数。要求所有边的出现顺序和题目中给出的相同。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

数据范围

本题启用 Special Judge 和 Subtask。

Subtask #1（ $30$ 分）： $\leq 10$ ， $\leq 20$ ；
Subtask #2（ $30$ 分）： $\leq 100$ ， $\leq 200$ ；
Subtask #3（ $40$ 分）： $\leq 1000$ ， $\leq 2000$ 。

保证数据中不会出现重边，自环。

P5590 赛车游戏差分约束

一，以1为起点BFS，如果无法到达N点，返回-1。
二，所有边反转，从N开始BFS。两轮BFS都到达的点才处理，有一轮没达到的点及相连的边删除。
三，假定各边的权重为1，求各节点到1的最长路leves[i]。如果有环(正环)，返回-1。
四，按leves[i] 从大到小枚举各节点，枚举i的后续节点j。m1 = min(leves[j]),m2=max(leves[j]),有leves[i] < leves[j]，故leves[i] < m1恒成立。确保leves[i] < m1的前提上，增加leves[i] 及其前置节点，使得leves[j]-leves[i] <=9.
第四步完成后，leves[j] - leves[i] 就是i到j 的权。如果leves[i] 有多个合法值，都要枚举。
综合3到5就是差分约束。leves[i] < leves[j] ,即levevs[i] -leves[j] <=-1,leves[j]-leves[i] <=9。由于levevs[i] -leves[j]<=-1,地图有环，差分系统的有向图也一定有环。
由于边权最大9，边数1000。故1e4就是极大值。增加0到各点权位1e4的边。以0为起点，求最小路径。

总结

删除非起点终点路径上的点和边后。起点到任意点的任意路径路程都相等，否则和起点到终点任意路径相等矛盾。vis[i]记录起点到i的最短路，也就是起点i到任意路径的路程。
u有边指向v，则：uv的边权是dis[v]-dis[u]，可以是1到9的任意值。
本题是差分约束的充分条件，故差分约束，无解，则本题无解。
下面用数学归纳法来证明差分的系统的解一定符合所有路径都是最短路。
经过0条边的路径，只有一条，一定符合本题。
如果经过i条边的路径都符合，则经过i+1条边的路径也符合。令第i+1条边是u $\rightarrow$ v，则此路径的路程是：dis[u]+(dis[v]-disv[u])= div[v]就是最短路。
注意：忽略的边任意权值。

代码

核心代码

#include 
#include 
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include 
#include 
#include
#include
#include

#include 
using namespace std;

template<class T1, class T2>
std::istream& operator >> (std::istream& in, pair<T1, T2>& pr) {
	in >> pr.first >> pr.second;
	return in;
}

template<class T1, class T2, class T3 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3>& t) {
	in >> get<0>(t) >> get<1>(t) >> get<2>(t);
	return in;
}

template<class T1, class T2, class T3, class T4 >
std::istream& operator >> (std::istream& in, tuple<T1, T2, T3, T4>& t) {
	in >> get<0>(t) >> get<1>(t) >> get<2>(t) >> get<3>(t);
	return in;
}

template<class T = int>
vector<T> Read() {
	int n;
	scanf("%d", &n);
	vector<T> ret(n);
	for (int i = 0; i < n; i++) {
		cin >> ret[i];
	}
	return ret;
}

template<class T = int>
vector<T> Read(int n) {
	vector<T> ret(n);
	for (int i = 0; i < n; i++) {
		cin >> ret[i];
	}
	return ret;
}

template<int N = 1'000'000>
class COutBuff
{
public:
	COutBuff() {
		m_p = puffer;
	}
	template<class T>
	void write(T x) {
		int num[28], sp = 0;
		if (x < 0)
			*m_p++ = '-', x = -x;

		if (!x)
			*m_p++ = 48;

		while (x)
			num[++sp] = x % 10, x /= 10;

		while (sp)
			*m_p++ = num[sp--] + 48;
		AuotToFile();
	}
	void writestr(const char* sz) {
		strcpy(m_p, sz);
		m_p += strlen(sz);
		AuotToFile();
	}
	inline void write(char ch)
	{
		*m_p++ = ch;
		AuotToFile();
	}
	inline void ToFile() {
		fwrite(puffer, 1, m_p - puffer, stdout);
		m_p = puffer;
	}
	~COutBuff() {
		ToFile();
	}
private:
	inline void AuotToFile() {
		if (m_p - puffer > N - 100) {
			ToFile();
		}
	}
	char  puffer[N], * m_p;
};

template<int N = 1'000'000>
class CInBuff
{
public:
	inline CInBuff() {}
	inline CInBuff<N>& operator>>(char& ch) {
		FileToBuf();
		ch = *S++;
		return *this;
	}
	inline CInBuff<N>& operator>>(int& val) {
		FileToBuf();
		int x(0), f(0);
		while (!isdigit(*S))
			f |= (*S++ == '-');
		while (isdigit(*S))
			x = (x << 1) + (x << 3) + (*S++ ^ 48);
		val = f ? -x : x; S++;//忽略空格换行		
		return *this;
	}
	inline CInBuff& operator>>(long long& val) {
		FileToBuf();
		long long x(0); int f(0);
		while (!isdigit(*S))
			f |= (*S++ == '-');
		while (isdigit(*S))
			x = (x << 1) + (x << 3) + (*S++ ^ 48);
		val = f ? -x : x; S++;//忽略空格换行
		return *this;
	}
	template<class T1, class T2>
	inline CInBuff& operator>>(pair<T1, T2>& val) {
		*this >> val.first >> val.second;
		return *this;
	}
	template<class T1, class T2, class T3>
	inline CInBuff& operator>>(tuple<T1, T2, T3>& val) {
		*this >> get<0>(val) >> get<1>(val) >> get<2>(val);
		return *this;
	}
	template<class T1, class T2, class T3, class T4>
	inline CInBuff& operator>>(tuple<T1, T2, T3, T4>& val) {
		*this >> get<0>(val) >> get<1>(val) >> get<2>(val) >> get<3>(val);
		return *this;
	}
	template<class T = int>
	inline CInBuff& operator>>(vector<T>& val) {
		int n;
		*this >> n;
		val.resize(n);
		for (int i = 0; i < n; i++) {
			*this >> val[i];
		}
		return *this;
	}
	template<class T = int>
	vector<T> Read(int n) {
		vector<T> ret(n);
		for (int i = 0; i < n; i++) {
			*this >> ret[i];
		}
		return ret;
	}
	template<class T = int>
	vector<T> Read() {
		vector<T> ret;
		*this >> ret;
		return ret;
	}
private:
	inline void FileToBuf() {
		const int canRead = m_iWritePos - (S - buffer);
		if (canRead >= 100) { return; }
		if (m_bFinish) { return; }
		for (int i = 0; i < canRead; i++)
		{
			buffer[i] = S[i];//memcpy出错			
		}
		m_iWritePos = canRead;
		buffer[m_iWritePos] = 0;
		S = buffer;
		int readCnt = fread(buffer + m_iWritePos, 1, N - m_iWritePos, stdin);
		if (readCnt <= 0) { m_bFinish = true; return; }
		m_iWritePos += readCnt;
		buffer[m_iWritePos] = 0;
		S = buffer;
	}
	int m_iWritePos = 0; bool m_bFinish = false;
	char buffer[N + 10], * S = buffer;
};

template<class T = int, T iDef = INT_MAX / 2>
class CDisNegativeRing //贝尔曼-福特算法
{
public:
	bool Dis(int N, vector<tuple<int, int, int>> edgeFromToW, int start) {
		vector<T> pre(N, iDef);
		pre[start] = 0;
		for (int t = 0; t < N; t++) {
			auto cur = pre;
			for (const auto& [u, v, w] : edgeFromToW) {
				cur[v] = min(cur[v], pre[u] + w);
			}
			if (t + 1 == N) {
				for (int i = 0; i < N; i++) {
					if (pre[i] != cur[i]) { return false; }
				}
			}
			pre.swap(cur);
		}
		m_vDis = pre;
		return true;
	}
	vector<T> m_vDis;
};

class CNeiBo
{
public:
	static vector<vector<int>> Two(int n, const vector<pair<int, int>>& edges, bool bDirect, int iBase = 0)
	{
		vector<vector<int>>  vNeiBo(n);
		for (const auto& [i1, i2] : edges)
		{
			vNeiBo[i1 - iBase].emplace_back(i2 - iBase);
			if (!bDirect)
			{
				vNeiBo[i2 - iBase].emplace_back(i1 - iBase);
			}
		}
		return vNeiBo;
	}
	static vector<vector<int>> Two(int n, const vector<vector<int>>& edges, bool bDirect, int iBase = 0)
	{
		vector<vector<int>>  vNeiBo(n);
		for (const auto& v : edges)
		{
			vNeiBo[v[0] - iBase].emplace_back(v[1] - iBase);
			if (!bDirect)
			{
				vNeiBo[v[1] - iBase].emplace_back(v[0] - iBase);
			}
		}
		return vNeiBo;
	}
	static vector<vector<std::pair<int, int>>> Three(int n, vector<vector<int>>& edges, bool bDirect, int iBase = 0)
	{
		vector<vector<std::pair<int, int>>> vNeiBo(n);
		for (const auto& v : edges)
		{
			vNeiBo[v[0] - iBase].emplace_back(v[1] - iBase, v[2]);
			if (!bDirect)
			{
				vNeiBo[v[1] - iBase].emplace_back(v[0] - iBase, v[2]);
			}
		}
		return vNeiBo;
	}
	static vector<vector<int>> Mat(vector<vector<int>>& neiBoMat)
	{
		vector<vector<int>> neiBo(neiBoMat.size());
		for (int i = 0; i < neiBoMat.size(); i++)
		{
			for (int j = i + 1; j < neiBoMat.size(); j++)
			{
				if (neiBoMat[i][j])
				{
					neiBo[i].emplace_back(j);
					neiBo[j].emplace_back(i);
				}
			}
		}
		return neiBo;
	}
};
class CBFSDis
{
public:
	CBFSDis(vector<vector<int>>& vNeiB, vector<int> start)
	{
		m_vDis.assign(vNeiB.size(), m_iNotMayDis);
		queue<int> que;
		for (const auto& n : start)
		{
			m_vDis[n] = 0;
			que.emplace(n);
		}
		while (que.size())
		{
			const int cur = que.front();
			que.pop();
			for (const auto next : vNeiB[cur])
			{
				if (m_iNotMayDis != m_vDis[next])
				{
					continue;
				}
				m_vDis[next] = m_vDis[cur] + 1;
				que.emplace(next);
			}
		}
	}
public:
	const int m_iNotMayDis = 1e9;
	vector<int> m_vDis;
};
class Solution {
public:
	vector<int> Ans(int N, const vector<pair<int, int>>& edge) {
		auto neiBo = CNeiBo::Two(N, edge, true, 1);
		vector<vector<int>> neiBoBack(N);
		for (int i = 0; i < N; i++) {
			for (const auto& j : neiBo[i]) {
				neiBoBack[j].emplace_back(i);
			}
		}
		CBFSDis dis1(neiBo, { 0 });
		if (dis1.m_iNotMayDis == dis1.m_vDis.back()) { return {}; }
		CBFSDis dis2(neiBoBack, { N - 1 });
		vector<tuple<int, int, int>> edge2;
		auto Not = [&](int i, int j) {
			if ((dis1.m_vDis[i] > N) || (dis1.m_vDis[j] > N)) { return true; }
			if ((dis2.m_vDis[i] > N) || (dis2.m_vDis[j] > N)) { return true; }
			return false;
		};
		for (auto [i, j] : edge) {
			i--, j--;
			if (Not(i, j)) { continue; }
			//eves[i] < leves[j] ,即levevs[i] -leves[j] <=-1,leves[j]-leves[i] <=9。由于levevs[i] -leves[j]<=-1,
			edge2.emplace_back(j, i, -1);
			edge2.emplace_back(i, j, 9);
		}
		CDisNegativeRing dis;
		if (!dis.Dis(N, edge2, 0)) { return {}; }
		vector<int> ans;
		for (auto [i, j] : edge) {
			i--, j--;
			if (Not(i, j)) { ans.emplace_back(9); continue; }
			ans.emplace_back(dis.m_vDis[j] - dis.m_vDis[i]);
		}
		return ans;
	}
};

int main() {
#ifdef _DEBUG
	freopen("a.in", "r", stdin);
#endif // DEBUG	
	ios::sync_with_stdio(0);
	int n, m ;
	cin >> n >> m ;	
	auto ope = Read<pair< int,int>>(m);
#ifdef _DEBUG		
	printf("n=%d", n);
	Out(ope, "edge=");
	//Out(ope, ",ope=");
	//Out(edge2, ",edge2=");
	/*Out(que, "que=");*/
#endif // DEBUG	
	auto res = Solution().Ans(n,ope);
	if (res.empty()) {
		cout << -1;
	}
	else {
		cout << n << " " << m << "\n";
		for (int i = 0; i < m; i++) {
			cout << ope[i].first << " " << ope[i].second << " " << res[i] << "\n";
		}
	}
	return 0;
}

单元测试

int n;
		vector<pair<int, int>> edge;
		TEST_METHOD(TestMethod1)
		{
			n = 3, edge = { {1,2} };
			auto res = Solution().Ans(n, edge);
			AssertV({}, res);
		}
		TEST_METHOD(TestMethod2)
		{
			n = 10,edge = { {1,2},{2,3},{3,4},{4,5},{5,6},{6,7},{7,8},{8,9},{9,10},{1,10} };
			auto res = Solution().Ans(n, edge);
			vector<int >act(edge.size(), 1);
			act.back() = 9;
			AssertV(act, res);
		}
		TEST_METHOD(TestMethod3)
		{
			n = 3, edge = { {1,3},{1,2} };
			auto res = Solution().Ans(n, edge);
			AssertV({9,9}, res);
		}

扩展阅读

我想对大家说的话
工作中遇到的问题，可以按类别查阅鄙人的算法文章，请点击《算法与数据汇总》。
学习算法：按章节学习《喜缺全书算法册》，大量的题目和测试用例，打包下载。重视操作
有效学习：明确的目标及时的反馈拉伸区（难度合适）专注
闻缺陷则喜(喜缺)是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛
失败+反思=成功成功+反思=成功

视频课程

先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

测试环境

操作系统：win7 开发环境： VS2019 C++17
或者操作系统：win10 开发环境： VS2022 C++17
如无特殊说明，本算法用**C++**实现。

算法及C++答疑请加群

QQ群名片

本文涉及知识点

P5590 赛车游戏

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

数据范围

P5590 赛车游戏 差分约束

总结

代码

核心代码

单元测试

扩展阅读

视频课程

测试环境

评论记录：

P5590 赛车游戏差分约束