引言

从本节开始，将介绍梯度下降法$(\text{Gradient Descent,GD})$。

回顾：线搜索方法

线搜索方法作为一种常见优化问题的策略，该方法的特点是：其迭代过程中，将数值解的方向和步长分开执行。对应数学符号表达如下：

• 其中${\mathcal{P}}_k$是一个向量，描述更新方向;${\alpha }_k$是一个$>0$的实数，表示步长。
• 由于我们更关注向量${\mathcal{P}}_k$的方向性，因而通常将其表示为单位向量,即$||{\mathcal{P}}_k||=1$。
  $$x_{k+1}=x_k+{\alpha }_k\cdot {\mathcal{P}}_k$$

线搜索方法的方向${\mathcal{P}}_k$

在线搜索方法——方向角度中介绍过：关于目标函数$f(\cdot )$的终极目标：$\underset{\mathcal{X}\in {\mathbb{R}}^n}{\min }f(\mathcal{X})$，如果数值解序列 { x k } k = 0 ∞ {x_k}_{k=0}^{infty} {xk​}k=0∞​对应的目标函数结果 { f ( x k ) } k = 0 ∞ {f(x_k)}_{k=0}^{infty} {f(xk​)}k=0∞​服从严格的单调性：
$$f(x_{k+1})<f(x_k)$$
那么必然有：

• 其中$[\nabla f(x_k)]$表示数值解$x_k$对应目标函数的梯度向量,详细推导过程见上方链接。
• ${\mathcal{P}}_k$化为单位向量产生的常数系数合并到${\alpha }_k$中。
  $$f(x_{k+1})-f(x_k)\approx [\nabla f(x_k){]}^T{\mathcal{P}}_k\cdot {\alpha }_k<0$$

从而将满足该条件的${\mathcal{P}}_k$称作下降方向$(\text{Descent Direction})$。将上式展开有：

• 其中${\theta }_k$表示向量$\nabla f(x_k)$与向量${\mathcal{P}}_k$之间的夹角。
• 在仅考虑方向角度对$f(x_{k+1})-f(x_k)$影响的情况下，将${\alpha }_k$忽略，不改变不等号方向。
  $$||\nabla f(x_k)||\cdot ||{\mathcal{P}}_k||\cdot \cos {\theta }_k<0$$

其中$||\nabla f(x_k)||,||{\mathcal{P}}_k||$均表示向量的模(均为固定的正值)，因而$\cos {\theta }_k\in [-1,0)$。当$\cos {\theta }_k=-1$时，$f(x_{k+1})-f(x_k)$可取得最小值，从而达到最佳的优化方向。而此时下降方向${\mathcal{P}}_k$与梯度方向$\nabla f(x_k)$方向相反。因此也称此时的${\mathcal{P}}_k$为最速下降方向：
其中$||\nabla f(x_k)||$是关于上一次迭代结果$x_k$的函数，因而是已知信息。
$${\mathcal{P}}_k=-\nabla f(x_k)$$

线搜索方法的步长${\alpha }_k$

关于当前迭代步骤的最优步长${\alpha }_k$通常有两种求解方式：

• 精确搜索：在${\mathcal{P}}_k$固定的情况下，选择使得$f(x_{k+1})$达到最小的步长结果作为当前迭代步骤的最优步长：
  其中$x_k,{\mathcal{P}}_k$是确定的信息，因此可将$f(x_{k+1})$视作关于$\alpha$的函数$\varphi (\alpha )$。
  $$\begin{array}{rl}{\alpha }_k& =\underset{\alpha >0}{\mathrm{argmin}}f(x_{k+1})\\ & =\underset{\alpha >0}{\mathrm{argmin}}f(x_k+\alpha \cdot {\mathcal{P}}_k)\\ & =\underset{\alpha >0}{\mathrm{argmin}}\varphi (\alpha )\end{array}$$
  具体求解方式就是：对$\alpha$求导，从而获取极值。但真实情况下，这种方式并不可取。
  • 关于目标函数$f(\cdot )$的复杂程度我们一无所知。关于梯度$\nabla f(x_k+\alpha \cdot {\mathcal{P}}_k)$可能非常复杂。
  • 这仅仅是一次迭代步骤的解。也就是说：每次迭代都要求解精确解。这无疑增加了迭代的计算代价，我们仅希望迭代产生的步长能够收敛到$\underset{k\Rightarrow \infty }{\lim }f(x_k)\Rightarrow f^{\ast }$，它的中间过程是否准确并不在乎。
    $$\{\begin{array}{l}\begin{array}{rl}& \frac{\partial \varphi (\alpha )}{\partial \alpha }={\varphi }^{\prime }(\alpha )=[\nabla f(x_k+\alpha \cdot {\mathcal{P}}_k){]}^T{\mathcal{P}}_k\\ & {\varphi }^{\prime }(\alpha )=0\Rightarrow {\alpha }_k\end{array}\end{array}$$
• 非精确搜索：相比于精确搜索，我们不计较迭代产生的步长结果是否最优，仅需要该结果能够帮助$f(x_k)$有效收敛即可：
  $$\underset{k\Rightarrow \infty }{\lim }f(x_k)\Rightarrow f^{\ast }$$
  常见的非精确方法有：$\text{Armijo}$准则，对$\text{Armijo}$准则进行优化的$\text{Glodstein}$准则，以及基于$\text{Armijo}$准则，对$\text{Armijo,Glodstein}$准则进行优化的$\text{Wolfe}$准则。
  这里不再赘述。

梯度下降方法整体介绍

梯度下降法是一种典型的线搜索方法。并且它的更新方向${\mathcal{P}}_k$就是最速下降方向：$-\nabla f(x_k)$。

• 梯度下降法也被称作最速下降法。
• 这个最速下降方向仅仅是每一个迭代步骤中向量$x_k$所在位置的最速下降方向，而不是全局最速下降方向。这与贪心算法类似，是一个局部最优。如下图:

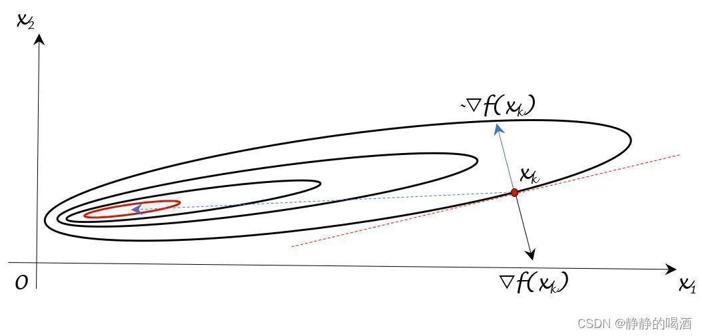
很明显，蓝色实线是指本次迭代步骤中的最优方向;而蓝色虚线是指全局最优方向。上图描述的是二维权重特征对应的迭代过程。如果权重特征只有一维特征(一维向量;标量)，对应图像表示如下：

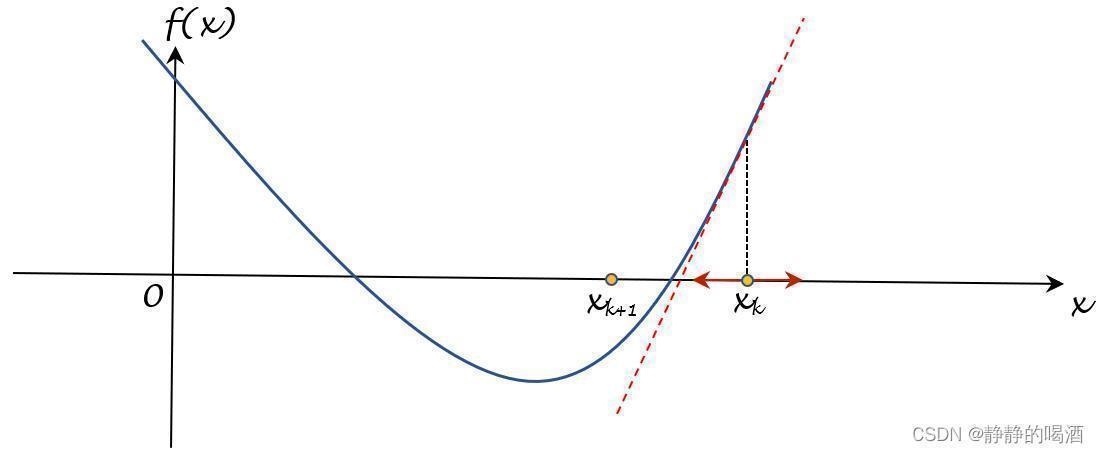
此时函数关于$x_k$的梯度$\nabla f(x_k)=[f^{\prime }(x_k){]}_{1\times 1}$,在迭代过程中寻找最优方向时，仅存在两个方向进行选择：沿着坐标轴与逆着坐标轴(红色箭头)。而此时$f^{\prime }(x_k)>0$,因而我们将数轴的正方向视作梯度方向；对应地，将数轴的反方向视作负梯度方向。针对当前的斜率信息，我们沿着负梯度方向更新到$x_{k+1}$。

关于梯度下降法的步长：

• 在后续过程中将介绍梯度下降法中如何求解精确步长，以及相应的限制条件。这里加一个传送门；

• 关于非精确搜索求解步长，这里补充一点关于各非精确搜索方法之间的一些逻辑上的关系。

  在简单认识$\text{Wolfe Condition}$的收敛性证明一节中介绍了使用$\text{Zoutendijk}$定理，验证了作用于$\text{Wolfe}$准则的步长结果可以使 { f ( x k ) } k = 1 ∞ {f(x_k)}_{k=1}^{infty} {f(xk​)}k=1∞​收敛。但实际上：$\text{Zoutendijk}$定理同样可以作用于$\text{Armijo,Glodstein}$准则，并证明其步长能够使 { f ( x k ) } k = 1 ∞ {f(x_k)}_{k=1}^{infty} {f(xk​)}k=1∞​收敛。

  由于$\text{Wolfe}$准则是基于$\text{Armijo}$准则提出的，其本质就是：在$\text{Armijo}$准则的基础上，那些梯度结果$\nabla f(x_{k+1})$过小的$\varphi (\alpha )$点对应的$\alpha$通过参数${\mathcal{C}}_2$消除掉了：
  Armijo Condition :  { ϕ ( α ) < f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α C 1 ∈ ( 0 , 1 ) Wolfe Condition :  { ϕ ( α ) ≤ f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ϕ ′ ( α ) ≥ C 2 ⋅ [ ∇ f ( x k ) ] T P k C 1 ∈ ( 0 , 1 ) C 2 ∈ ( C 1 , 1 )

  $$egin{aligned} & ext{Armijo Condition : }egin{cases} phi(alpha) < f(x_k) + mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k cdot alpha \ quad \ mathcal C_1 in (0,1) end{cases} \ & ext{Wolfe Condition : }egin{cases} phi(alpha) leq f(x_k) + mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k cdot alpha \ phi'(alpha) geq mathcal C_2 cdot [ abla f(x_k)]^T mathcal P_k \ mathcal C_1 in (0,1) \ mathcal C_2 in (mathcal C_1,1) end{cases} end{aligned}$$ ​Armijo Condition : ⎩ ⎨ ⎧​ϕ(α)<f(xk​)+C1​⋅[∇f(xk​)]TPk​⋅αC1​∈(0,1)​Wolfe Condition : ⎩ ⎨ ⎧​ϕ(α)≤f(xk​)+C1​⋅[∇f(xk​)]TPk​⋅αϕ′(α)≥C2​⋅[∇f(xk​)]TPk​C1​∈(0,1)C2​∈(C1​,1)​​
  反过来说：$\text{Armijo}$准则相当于$\text{Wolfe}$准则的一种极端情况：在${\mathcal{C}}_1$确定划分边界的基础上，一个$\alpha$都不去除，即：${\mathcal{C}}_2=1$。
  同理，$\text{Glodstein}$准则也是$\text{Wolfe}$准则中的一种情况。与$\text{Armijo}$这种极端情况不同的是，$\text{Glodstein}$准则更像是一种取巧情况：在$\begin{array}{r}{\mathcal{C}}_1\in \left(0,\frac{1}{2}\right)\end{array}$确定划分边界的基础上，选择一个合适的$\begin{array}{r}{\mathcal{C}}_2\in \left(\frac{1}{2},1\right)\end{array}$使得斜率分别为${\mathcal{C}}_1\cdot [\nabla f(x_k){]}^T{\mathcal{P}}_k$和${\mathcal{C}}_2\cdot [f(x_k){]}^T{\mathcal{P}}_k$的直线关于斜率为$\begin{array}{r}\frac{1}{2}[\nabla f(x_k){]}^T{\mathcal{P}}_k\end{array}$直线对称。
  因为在${\mathcal{C}}_1\in \begin{array}{r}\left(0,\frac{1}{2}\right)\end{array}$情况下，$\text{Wolfe}$准则关于${\mathcal{C}}_2$的描述范围$({\mathcal{C}}_1,1)$必然大于$\begin{array}{r}\left(\frac{1}{2},1\right)\end{array}$。因此必然能够找到这个合适的点，从而使该点情况下$\text{Wolfe}$准则等价于$\text{Glodstein}$准则。

关于梯度下降法的收敛速度：相比梯度下降法的收敛性，我们更关心在已知收敛的情况下，它的收敛速度情况。在上一节中对收敛速度进行了简单认识：

• 从收敛速度判别标准的角度划分，介绍了$\mathcal{Q}$-收敛速度与$\mathcal{R}$-收敛速度；
• 从收敛速度强度的角度划分(以$\mathcal{Q}$-收敛速度为例)，介绍了$\mathcal{Q}$-次线性收敛/线性收敛/超线性收敛/二次收敛。

而在梯度下降法中，它的收敛速度取决于目标函数$f(\cdot )$自身的性质：

• 关于目标函数$f(\cdot )$的基础条件：向下有界，在定义域内可微(至少局部可微)；
  如果不可微，我们甚至没有办法求解梯度，更不要说梯度的更新了。

• 要求$f(\cdot )$至少是局部凸函数，并且其梯度$\nabla f(\cdot )$必然服从利普希兹连续。而利普希兹连续的作用在于：目标函数梯度$\nabla f(\cdot )$的变化量被常数$\mathcal{L}$限制住。或者说：$\nabla f(\cdot )$的变化不会过于剧烈。

  相反，如果不对$\nabla f(\cdot )$进行约束，很容易会出现梯度爆炸。因为可能存在：目标函数梯度可能在某一范围内飙升至极大。

在综上条件下，可达到次线性收敛级别的收敛速度。

在上述条件的基础上，如果$f(\cdot )$是一个强凸函数$(\text{Strong Convex Function})$，可达到线性收敛级别的收敛速度。
关于凸函数的强度性质：凸函数$<$严格凸函数$<$强凸函数。在后续进行介绍。传送门

在第二种条件的基础上：如果$f(\cdot )$仍然是一个强凸函数，并且$f(\cdot )$在其定义域内二阶可微，其对应的$\text{Hession Matrix}{\nabla }^{2}f(\cdot )$存在并满足：

• 其中$\mathcal{L}$依然是利普希兹连续中的具有限制作用的常数;$\preccurlyeq$表示矩阵小于等于;$\mathcal{I}$表示单位矩阵。
• 关于$\begin{array}{r}\frac{||\nabla f(x)-\nabla f(y)||}{||x-y||}={\nabla }^{2}f(\xi )\end{array}$详见拉格朗日中值定理。
  $$\forall x,y\in {\mathbb{R}}^n:\begin{array}{r}\frac{||\nabla f(x)-\nabla f(y)||}{||x-y||}={\nabla }^{2}f(\xi )\preccurlyeq \mathcal{L}\cdot \mathcal{I}\end{array}$$

同样可以达到线性收敛级别的收敛速度。

相关参考：
【优化算法】梯度下降法-总体介绍