机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索,Wolfe Condition]
引言
上一节介绍了 Glodstein ext{Glodstein} Glodstein准则 ( Glodstein Condition ) ( ext{Glodstein Condition}) (Glodstein Condition)及其弊端。本节将针对该弊端,介绍 Wolfe ext{Wolfe} Wolfe准则 ( Wolfe Condition ) ( ext{Wolfe Condition}) (Wolfe Condition)。
回顾:
Armijo ext{Armijo} Armijo准则及其弊端
在当前迭代步骤中,为了能够得到更精炼的
ϕ
(
α
)
phi(alpha)
ϕ(α)选择范围,
Armijo
ext{Armijo}
Armijo准则
(
Armijo Condition
)
( ext{Armijo Condition})
(Armijo Condition)提出一种关于
ϕ
(
α
)
phi(alpha)
ϕ(α)的筛选方式,使其比
ϕ
(
α
)
<
f
(
x
k
)
phi(alpha) < f(x_k)
ϕ(α)<f(xk)更加严格:
Armijo Condition :
{
ϕ
(
α
)
<
L
(
α
)
=
f
(
x
k
)
+
C
1
⋅
[
∇
f
(
x
k
)
]
T
P
k
⋅
α
C
1
∈
(
0
,
1
)
ext{Armijo Condition : } {ϕ(α)<L(α)=f(xk)+C1⋅[∇f(xk)]TPk⋅αC1∈(0,1)
这种操作产生的弊端是:
C
1
mathcal C_1
C1在取值过程中,可能出现数量较少的、并且并非
ϕ
(
α
)
phi(alpha)
ϕ(α)主要部分的选择空间。见下图:
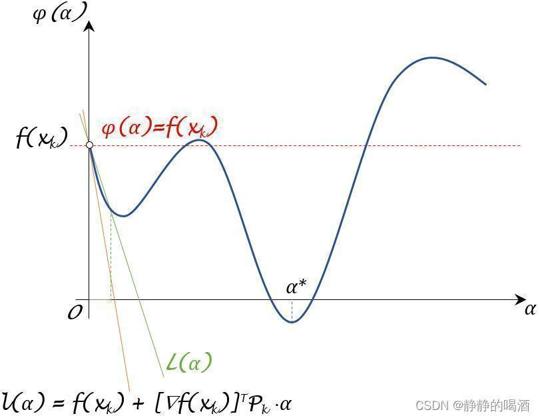
这种情况可能导致:
下面的两种情况都指向同一个问题:
L
(
α
)
mathcal L(alpha)
L(α)所划分的
α
alpha
α范围从整个
ϕ
(
α
)
phi(alpha)
ϕ(α)角度观察,是片面的、局部的。
- 可选择的 α alpha α范围较小;
- 该小范围内的
α
alpha
α结果,其对应的
ϕ
(
α
)
phi(alpha)
ϕ(α)并不优质。
这里的‘优质’是指与整个ϕ ( α ) phi(alpha) ϕ(α)函数结果相比都属于一个较小的结果。最优质的自然是α ∗ = arg min α > 0 ϕ ( α ) alpha^* = mathop{argmin}limits_{alpha > 0} phi(alpha) α∗=α>0argminϕ(α),但我们在每次迭代过程中并不执著于α ∗ alpha^* α∗,仅希望选择出的α alpha α结果能够有效地使{ f ( x k ) } k = 0 ∞ {f(x_{k})}_{k=0}^{infty} {f(xk)}k=0∞收敛到最优值f ∗ f^* f∗。
Glodstein ext{Glodstein} Glodstein准则及其弊端
针对
Armijo
ext{Armijo}
Armijo准则的问题,
Glodstein
ext{Glodstein}
Glodstein准则在其基础上添加一个下界:
Glodstein Condition :
{
f
(
x
k
)
+
(
1
−
C
)
⋅
[
∇
f
(
x
k
)
]
T
P
k
⋅
α
⏟
Lower Bound
≤
ϕ
(
α
)
≤
f
(
x
k
)
+
C
⋅
[
∇
f
(
x
k
)
]
T
P
k
⋅
α
C
∈
(
0
,
1
2
)
ext{Glodstein Condition : } {f(xk)+(1−C)⋅[∇f(xk)]TPk⋅α⏟Lower Bound≤ϕ(α)≤f(xk)+C⋅[∇f(xk)]TPk⋅αC∈(0,12)
其中分别描述上界、下界的划分函数:
-
Upper Bound :
L
U
(
α
)
=
f
(
x
k
)
+
C
⋅
[
∇
f
(
x
k
)
]
T
P
k
⋅
α
ext{Upper Bound : } LU(α)=f(xk)+C⋅[∇f(xk)]TPk⋅αUpper Bound : LU(α)=f(xk)+C⋅[∇f(xk)]TPk⋅α
LU(α)=f(xk)+C⋅[∇f(xk)]TPk⋅α - Lower Bound : L L ( α ) = f ( x k ) + ( 1 − C ) ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ext{Lower Bound : } mathcal L_{mathcal L}(alpha) = f(x_k) + (1 - mathcal C) cdot [ abla f(x_k)]^T mathcal P_k cdot alpha Lower Bound : LL(α)=f(xk)+(1−C)⋅[∇f(xk)]TPk⋅α
关于
f
(
x
k
)
+
1
2
[
∇
f
(
x
k
)
]
T
P
k
⋅
α
f(xk)+12[∇f(xk)]TPk⋅α
其中两条绿色实线之间区域内的
ϕ
(
α
)
phi(alpha)
ϕ(α)结果相比
Armijo
ext{Armijo}
Armijo准则,其描述的范围更加核心。
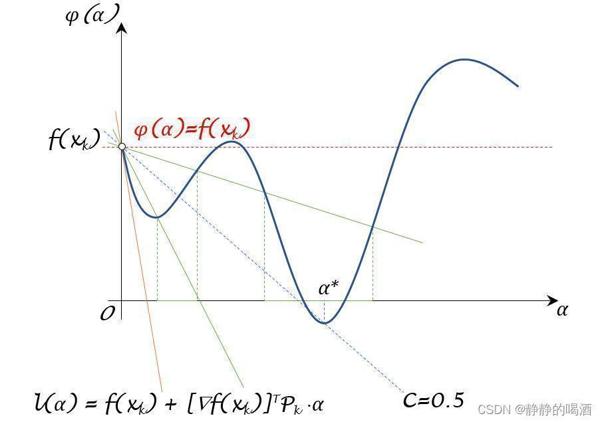
但
Goldstein
ext{Goldstein}
Goldstein准则自身同样存在弊端:当参数
C
mathcal C
C靠近
1
2
12
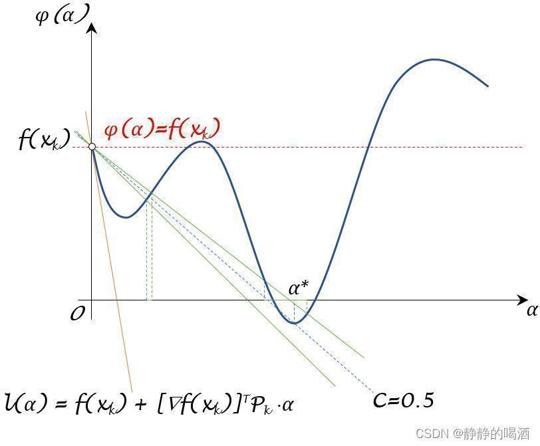
Wolfe Condition ext{Wolfe Condition} Wolfe Condition
首先,我们可以发现一个关于
Armijo
ext{Armijo}
Armijo准则与
Goldstein
ext{Goldstein}
Goldstein准则的共同问题:被选择的仅仅是满足划分边界条件的
α
alpha
α结果,而被选择的
α
alpha
α结果是否存在被选择的意义是未知的。
换句话说,基于这两种准则选择出的
α
alpha
α结果仅仅是因为:
该α alpha α对应的ϕ ( α ) phi(alpha) ϕ(α)位于决策边界L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α mathcal L(alpha) = f(x_k) + mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k cdot alpha L(α)=f(xk)+C1⋅[∇f(xk)]TPk⋅α的下方( Armijo Condition ) ( ext{Armijo Condition}) (Armijo Condition);该α alpha α对应的ϕ ( α ) phi(alpha) ϕ(α)位于上决策边界L U ( α ) mathcal L_{mathcal U}(alpha) LU(α)与下决策边界L L ( α ) mathcal L_{mathcal L}(alpha) LL(α)所围成的范围之间( Glodstein Condition ) ( ext{Glodstein Condition}) (Glodstein Condition)。
这意味着:我们确实得到了若干 α alpha α结果,但是这些结果是否优质属于未知状态。
我们尝试从满足
Armijo
ext{Armijo}
Armijo准则的基础上,通过某种规则剔除掉部分没有竞争力的
α
alpha
α结果,从而在剩余结果中找到优质的
α
alpha
α结果。见下图:
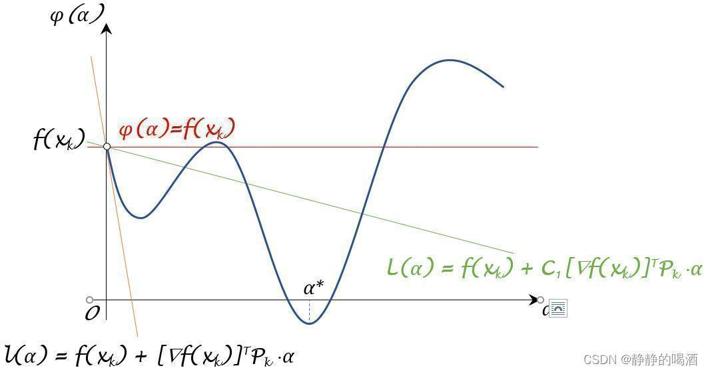
初始状态下,我们找到了一个
C
1
∈
(
0
,
1
)
mathcal C_1 in (0,1)
C1∈(0,1),并描述出了它的划分边界
L
(
α
)
mathcal L(alpha)
L(α);由于
L
(
α
)
mathcal L(alpha)
L(α)的斜率
C
1
⋅
[
∇
f
(
x
k
)
]
T
P
k
mathcal C_1 cdot [
abla f(x_k)]^T mathcal P_k
C1⋅[∇f(xk)]TPk必然大于
l
(
α
)
l(alpha)
l(α)的斜率
[
∇
f
(
x
k
)
]
T
P
k
[
abla f(x_k)]^T mathcal P_k
[∇f(xk)]TPk,因此从
α
=
0
alpha = 0
α=0出发,找到切线斜率与
L
(
α
)
mathcal L(alpha)
L(α)斜率相同的点:
下图中的绿色虚线表示切线斜率与
L
(
α
)
mathcal L(alpha)
L(α)斜率相同的
α
alpha
α点,短绿线表示寻找过程,点
A
mathcal A
A表示满足条件的切点。
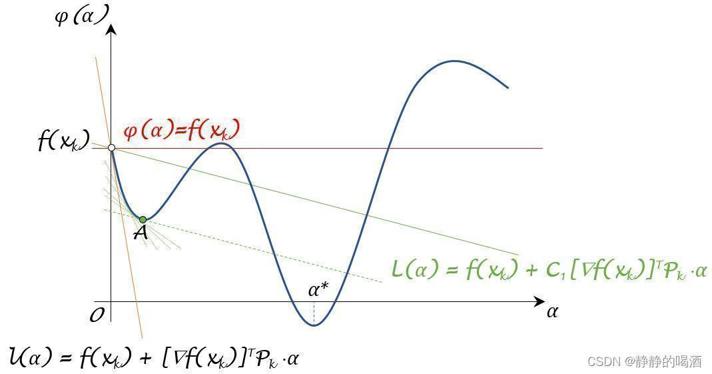
通过观察可以发现:点
A
mathcal A
A必然不是极值点(虽然看起来有点像~),因为该点处的斜率
≠
0
eq 0
=0。这里能够确定:从
[
0
,
f
(
x
k
)
]
[0,f(x_k)]
[0,f(xk)]到
A
mathcal A
A点这一段函数内的所有点相比于
A
mathcal A
A都没有竞争力。而这些点的切线斜率
ϕ
′
(
α
)
phi'(alpha)
ϕ′(α)满足:
[
∇
f
(
x
k
)
]
T
P
k
≤
ϕ
′
(
α
)
≤
C
1
⋅
[
∇
f
(
x
k
)
]
T
P
k
[
abla f(x_k)]^T mathcal P_k leq phi'(alpha) leq mathcal C_1 cdot [
abla f(x_k)]^T mathcal P_k
[∇f(xk)]TPk≤ϕ′(α)≤C1⋅[∇f(xk)]TPk
关于仅与参数 C 1 mathcal C_1 C1相关的武断做法
如果将这些没有竞争力的点去除掉,保留剩余的点,结合 Armijo ext{Armijo} Armijo准则,会有如下的步长 α alpha α选择方式:
其中ϕ ′ ( α ) = ∂ f ( x k + α ⋅ P k ) ∂ α = [ ∇ f ( x k + α ⋅ P k ) ] T P k ϕ′(α)=∂f(xk+α⋅Pk)∂α=[∇f(xk+α⋅Pk)]TPkϕ′(α)=∂α∂f(xk+α⋅Pk)=[∇f(xk+α⋅Pk)]TPk,在后续的计算中均简化写作ϕ ′ ( α ) phi'(alpha) ϕ′(α)。关于斜率ϕ ′ ( α ) ≤ C 1 ⋅ [ ∇ f ( x k ) ] T P k phi'(alpha)leq mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k ϕ′(α)≤C1⋅[∇f(xk)]TPk点不再理会,而[ ∇ f ( x k ) ] T P k [ abla f(x_k)]^T mathcal P_k [∇f(xk)]TPk是ϕ ( 0 ) phi(0) ϕ(0)的斜率,作为下界。
{ ϕ ( α ) ≤ f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ϕ ′ ( α ) ≥ C 1 ⋅ [ ∇ f ( x k ) ] T P k C 1 ∈ ( 0 , 1 ) {ϕ(α)≤f(xk)+C1⋅[∇f(xk)]TPk⋅αϕ′(α)≥C1⋅[∇f(xk)]TPkC1∈(0,1)⎩ ⎨ ⎧ϕ(α)≤f(xk)+C1⋅[∇f(xk)]TPk⋅αϕ′(α)≥C1⋅[∇f(xk)]TPkC1∈(0,1)
基于上述逻辑,被选择的
ϕ
(
α
)
phi(alpha)
ϕ(α)见下图:
其中
A
′
mathcal A'
A′点表示该图像中斜率与
L
(
α
)
mathcal L(alpha)
L(α)相同的其他位置的点。
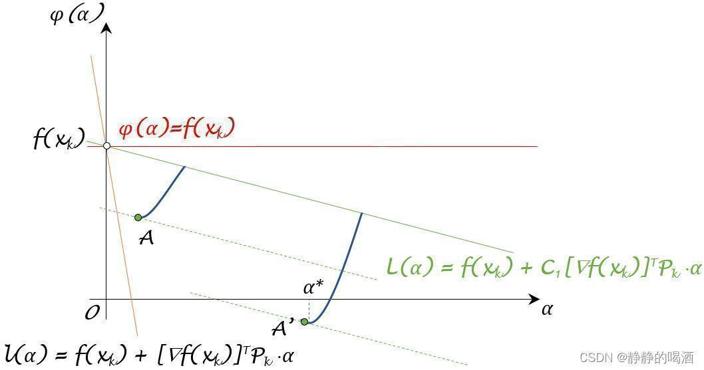
上述这种方式可取吗 ? ? ?从逻辑角度上是可行的,但不可取。
关于 C 1 mathcal C_1 C1武断做法不可取的逻辑解释
-
由于 C 1 ∈ ( 0 , 1 ) mathcal C_1 in (0,1) C1∈(0,1),因而 C 1 ⋅ [ ∇ f ( x k ) ] T P k < 0 mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k < 0 C1⋅[∇f(xk)]TPk<0恒成立。也就是说:无论 C 1 mathcal C_1 C1如何趋近于 0 0 0, Armijo ext{Armijo} Armijo准则划分边界 L ( α ) mathcal L(alpha) L(α)如何趋近于 ϕ ( α ) = f ( x k ) phi(alpha) = f(x_k) ϕ(α)=f(xk),都无法获取使 ϕ ′ ( α ) = 0 phi'(alpha) = 0 ϕ′(α)=0的极值解。
很简单,就是因为取不到~而与此同时,我们为了追求这个极值解,可能反而会损失一系列 ϕ ( α ) phi(alpha) ϕ(α)优质的 α alpha α点。
如果仅使用C 1 mathcal C_1 C1一个参数,那么要去除的点在Armijo ext{Armijo} Armijo准则划分边界L ( α ) mathcal L(alpha) L(α)确定的那一刻就已经被确定了,这势必会误伤一些ϕ ( α ) phi(alpha) ϕ(α)优质的α alpha α结果。 -
其次,这里的操作是非精确搜索,因而不执著去追求极值解(那不就变成精确搜索了吗~),并且这仅仅是一次迭代的计算过程,没有必要消耗计算代价去追求更优质的 ϕ ( α ) phi(alpha) ϕ(α),这也是我们希望尽量保留 ϕ ( α ) phi(alpha) ϕ(α)优质解的核心原因:
与上一张图被选择的ϕ ( α ) phi(alpha) ϕ(α)值对比观察,红色椭圆形虚线区域中描述的ϕ ( α ) phi(alpha) ϕ(α)值是比较优质的,但因为C 1 mathcal C_1 C1的原因导致该部分结果被‘一刀切’了。这并不是我们希望看到的结果。
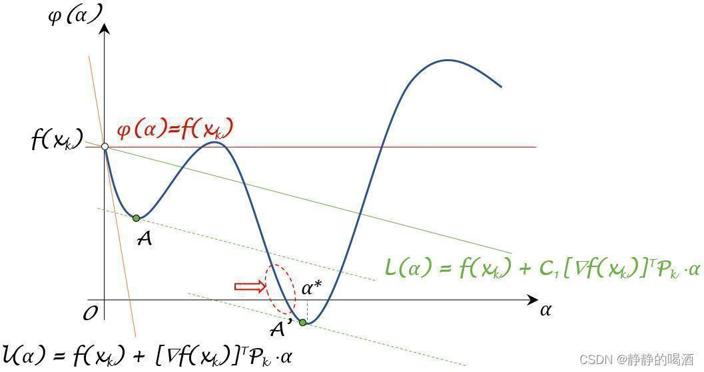
关于 C 1 mathcal C_1 C1武断做法的改进: Wolfe Condition ext{Wolfe Condition} Wolfe Condition
如何避免上述一刀切的情况出现 ? ? ? Wolfe ext{Wolfe} Wolfe准则提供了而一种更软性的操作。
设置一个参数 C 2 ∈ ( C 1 , 1 ) mathcal C_2 in (mathcal C_1,1) C2∈(C1,1),该参数对应的斜率表示为 C 2 ⋅ [ ∇ f ( x k ) ] T P k mathcal C_2 cdot [ abla f(x_k)]^T mathcal P_k C2⋅[∇f(xk)]TPk,而该斜率在 ( [ ∇ f ( x k ) ] T P k , C 1 ⋅ [ ∇ f ( x k ) ] T P k ) ([ abla f(x_k)]^T mathcal P_k,mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k ) ([∇f(xk)]TPk,C1⋅[∇f(xk)]TPk)之间滑动(变换)。此时会出现一种缓和的情况:即便假设 C 1 mathcal C_1 C1无限接近于 0 0 0,但由于 C 2 mathcal C_2 C2的作用,使 ϕ ( α ) phi(alpha) ϕ(α)点的选择与 C 1 mathcal C_1 C1没有太大关联:
这里相当于将斜率C 1 ⋅ [ ∇ f ( x k ) ] T P k mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k C1⋅[∇f(xk)]TPk视作一个边界。上面的一刀切情况相当于C 1 ⇒ 0 mathcal C_1 Rightarrow 0 C1⇒0的同时,C 2 ⇒ C 1 mathcal C_2 Rightarrowmathcal C_1 C2⇒C1的情况。由于C 2 ∈ ( C 1 , 1 ) mathcal C_2 in (mathcal C_1,1) C2∈(C1,1)因而完全可以通过调整 C 2 mathcal C_2 C2针对那些斜率小于 C 1 ⋅ [ ∇ f ( x k ) ] T P k mathcal C_1 cdot [ abla f(x_k)]^T mathcal P_k C1⋅[∇f(xk)]TPk,但 ϕ ( α ) phi(alpha) ϕ(α)优质的结果进行酌情选择。
最终根据
Armijo
ext{Armijo}
Armijo准则,
Wolfe
ext{Wolfe}
Wolfe准则操作如下:
{
ϕ
(
α
)
≤
f
(
x
k
)
+
C
1
[
∇
f
(
x
k
)
]
T
P
k
⋅
α
ϕ
′
(
α
)
≥
C
2
⋅
[
∇
f
(
x
k
)
]
T
P
k
C
1
∈
(
0
,
1
)
C
2
∈
(
C
1
,
1
)
{ϕ(α)≤f(xk)+C1[∇f(xk)]TPk⋅αϕ′(α)≥C2⋅[∇f(xk)]TPkC1∈(0,1)C2∈(C1,1)
个人理解: Wolfe ext{Wolfe} Wolfe准则与 Armijo ext{Armijo} Armijo准则
在开头部分提到关于 Armijio ext{Armijio} Armijio准则的弊端,在介绍完 Wolfe ext{Wolfe} Wolfe准则之后,有种 Armijo ext{Armijo} Armijo准则的弊端卷土重来的感觉。个人认为: Wolfe ext{Wolfe} Wolfe准则提出的这种基于 C 2 ∈ ( C 1 , 1 ) mathcal C_2 in (mathcal C_1,1) C2∈(C1,1)的软性下界同样也在影响 C 1 mathcal C_1 C1的选择:
- 如果是单纯的 Armijo ext{Armijo} Armijo准则,我们可能更偏好 C 1 mathcal C_1 C1远离 0 0 0一些。因为 C 1 ⇒ 0 mathcal C_1 Rightarrow 0 C1⇒0意味着这种状态越趋近优化算法(四)中描述的必要不充分条件;这种 C 1 mathcal C_1 C1的选择方式也势必会增加 Armijo ext{Armijo} Armijo准则弊端的风险;
- 而 Wolfe ext{Wolfe} Wolfe准则中,即便 C 1 mathcal C_1 C1偏向 0 0 0方向,我们依然可以通过调整 C 2 mathcal C_2 C2对相对不优质的 ϕ ( α ) phi(alpha) ϕ(α)点进行过滤。从剩余的优质点中选择并进行迭代。

评论记录:
回复评论: