推荐|欧拉回路与哈密尔顿回路: Fleury算法与Hierholzer 算法(C++)

id="article_content" class="article_content clearfix"> id="content_views" class="markdown_views prism-dracula">

图论相关帖子

环境要求

本文所用样例在Windows 11以及Ubuntu 24.04上面编译通过.

Windows: 使用[Visual Studio],
Ubuntu: 使用 Clang 18.1.3. (Ubuntu 24.04 系统安装版本)
GCC 无法编译直接本项目代码, 因为本文代码使用了 C++20 Module, 而 GCC 对此支持不完整.

概念定义

图论中的回路是指一个路径, 它从某个顶点开始, 经过所有边恰好一次, 并回到起始顶点.

欧拉回路: 从一个顶点出发, 经过每条边恰好一次, 并且最终回到起始顶点.
哈密尔顿回路: 从一个顶点出发, 经过每个顶点恰好一次, 并且最终回到起始顶点.
欧拉路径: 从一个顶点出发, 访问图中的每一个边恰好一次, 但不需要回到起始顶点.
哈密尔顿路径: 从一个顶点出发, 访问图中的每一个其他顶点恰好一次, 但不需要回到起始顶点.

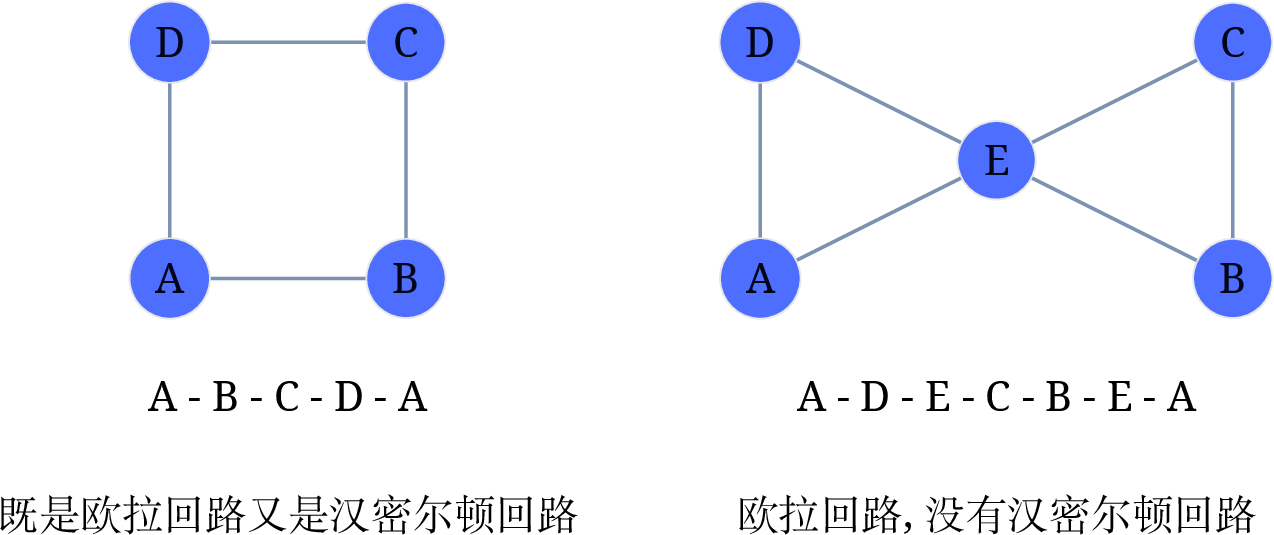
sample

欧拉回路

无向图的条件

对于无向图, 构成欧拉回路的充要条件是: 所有顶点的度数都必须是偶数.
如果仅有两个顶点的度数为奇数, 则存在从其中一个顶点到另一个顶点的欧拉路径, 但不是欧拉回路.

柯尼斯堡

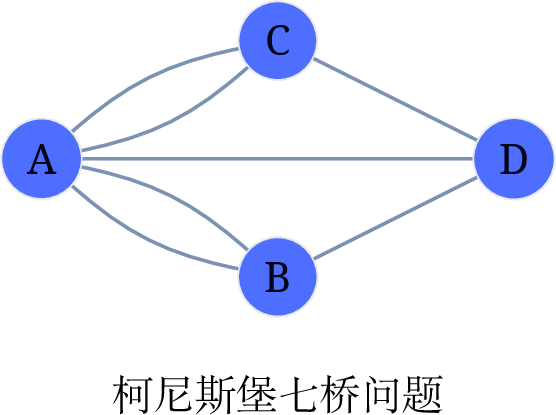
欧拉证明七桥问题没有解, 因为存在度为奇数的顶点.

有向图的条件

对于有向图, 每个顶点的入度必须等于出度才能构成欧拉回路.
如果仅有一个顶点的出度比入度多 1, 且另一个顶点的入度比出度多 1, 其余顶点的出入度相等, 则存在从出度多 1 的顶点到入度多 1 的顶点的欧拉路径.

求解算法

求解欧拉回路的主要算法包括 Fleury 算法和 Hierholzer 算法:

Fleury 算法解析

Fleury 算法是一种较为直观的方法, 逐步构造欧拉回路, 但其效率较低, 因为需要检查每一步是否会破坏图的连通性.

算法步骤如下:

选择起点:
- 如果图中存在欧拉回路, 则可以从任意顶点开始.
- 如果图中只存在欧拉路径, 则必须从度数为奇数的两个顶点之一开始.
遍历边:
- 从当前顶点出发, 选择下一条边进行遍历.
- 除非没有其他选择, 不然需要避免选择"桥"(或者说割边). 判断某条边是否为桥梁可以通过暂时移除该边并检查图是否仍然连通来实现. 加入断开了这条边之后, 原先的图不再相连, 则此边是一个桥.
标记已访问的边: 每次选择一条边后, 将其标记为已访问, 并将其从图中移除(或者记录下来以便后续恢复).
移动到下一个顶点: 移动到所选边的另一端点, 并重复上述过程, 直到所有边都被访问过.
返回起点:
- 如果是从欧拉回路的起点开始, 则最终会回到该起点, 形成一个闭合回路.
- 如果是从欧拉路径的一个端点开始, 则最终会到达另一个端点, 形成一条欧拉路径.

示例

求下图的欧拉路径:

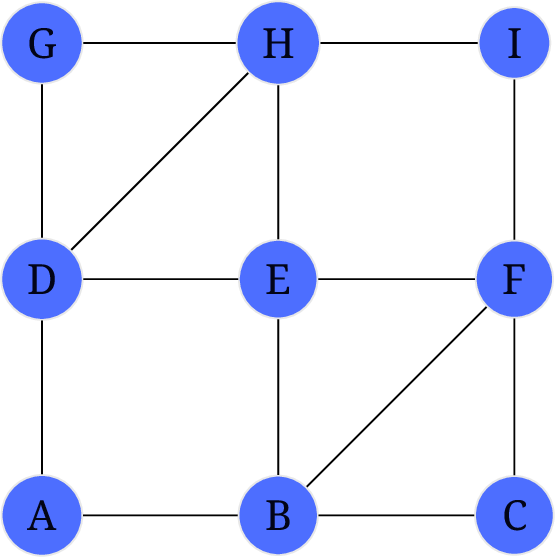
sample

fleury 算法步骤:

任意选定起点, 假定选择了A., A有两条边, 均不是桥, 任选一个都可以. 假定我们选择了A-B. 此时结果如下: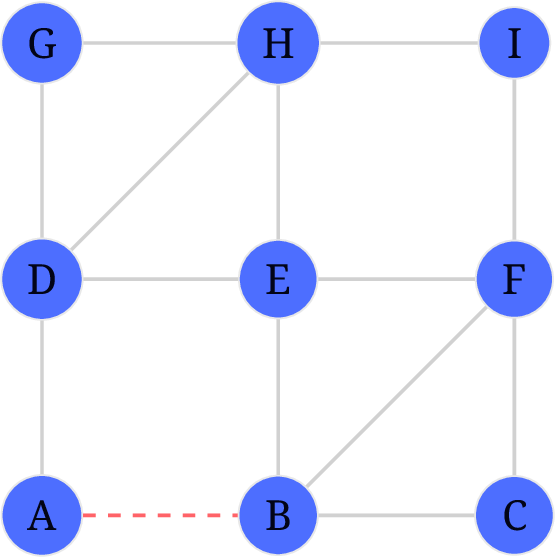
此时我们到达了B, B的的三条边均不是桥, 任选其一. 假定选了B-E. 结果如下: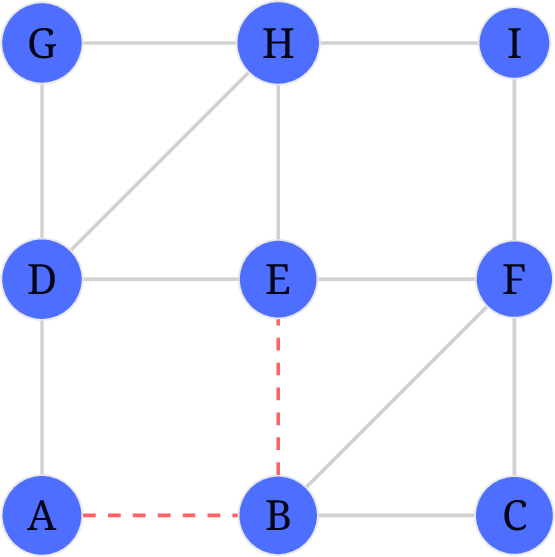
此时我们到达了E, 三条边均可选假定选了E-D. 结果如下: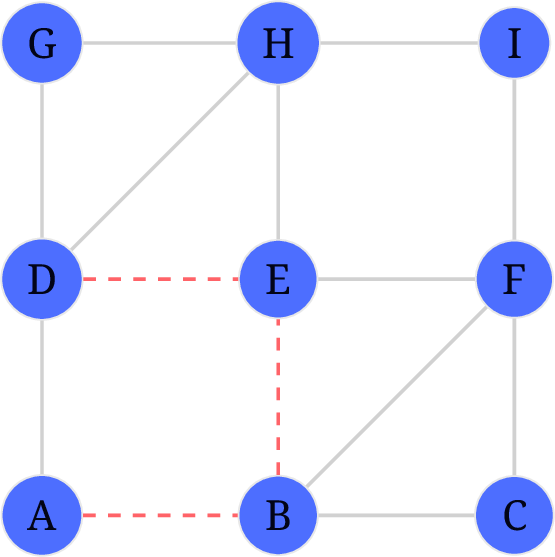
现在到达了D, 注意D-A是一个桥, 因为此时还有其他边可选, 所不能选D-A.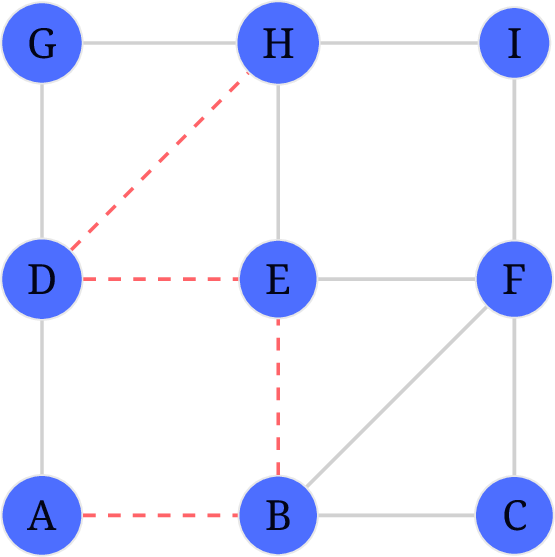
后续步骤不再赘述, 看 gif.

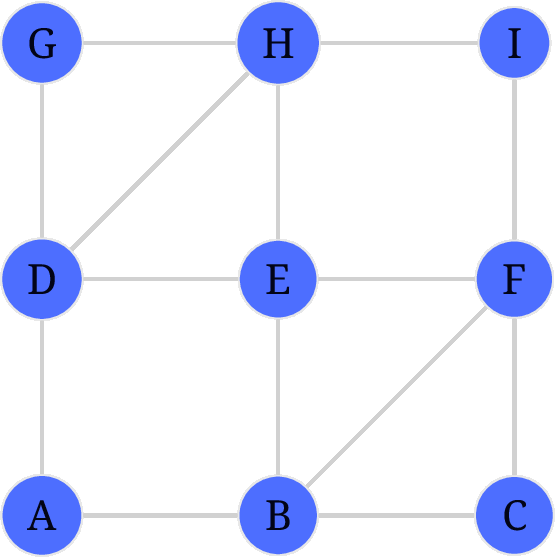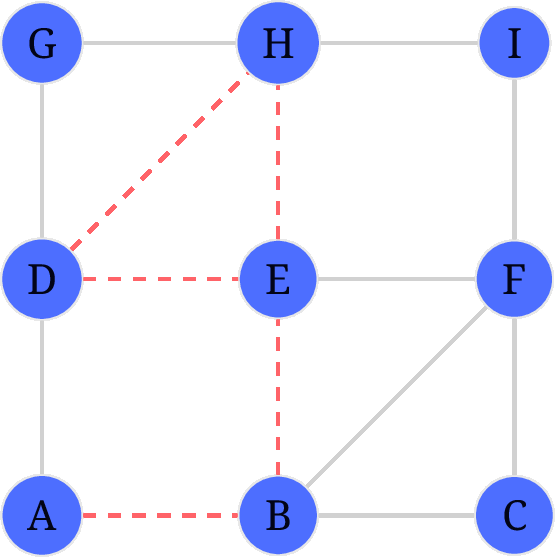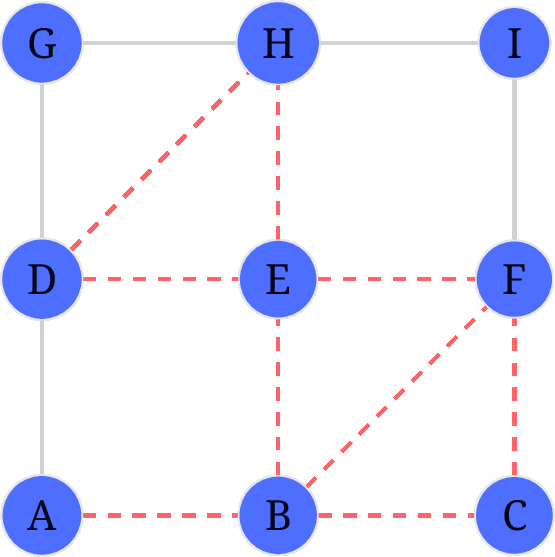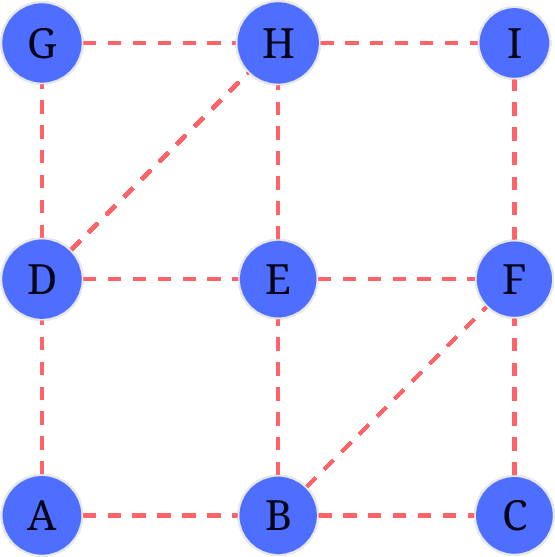
Hierholzer 算法

Hierholzer 算法是一个更为高效的方法, 通过利用回路合并的思想来构建欧拉回路. 它的基本思想是从任意一个顶点开始, 尝试访问每一条边, 并将访问过的边移除, 直到无法继续前进时, 再回溯寻找新的未访问边, 直到所有的边都被访问过为止.

算法步骤

选择起点:
- 从任意一个顶点开始(对于欧拉回路, 任何顶点都可以作为起点; 对于欧拉路径, 则需要从度数为奇数的顶点之一开始).
初始化路径:
- 创建一个空列表 path 来存储当前找到的路径.
- 创建一个栈 stack 并将起点压入栈中.
遍历边:
- 当栈不为空时, 执行以下操作:
  1. 弹出栈顶元素: 将栈顶元素取出并设为当前顶点 current_vertex.
  2. 检查相邻边: 检查当前顶点的所有未访问过的相邻边.
  3. 如果存在未访问的边:
    - 随机选择一条未访问的边, 并将其标记为已访问.
    - 将该边的另一端点推入栈中.
  4. 如果没有未访问的边:
    - 将当前顶点添加到 path 列表中.
合并路径:
- 当栈为空时, path 列表中的顶点顺序即为所求的欧拉回路. 但由于我们是从后往前添加顶点的, 因此需要反转 path 列表.
返回结果:
- 返回反转后的 path 列表, 这就是所求的欧拉回路.

示例演示

针对上题中提到的样例, hierholzer 的步骤如下图所示:

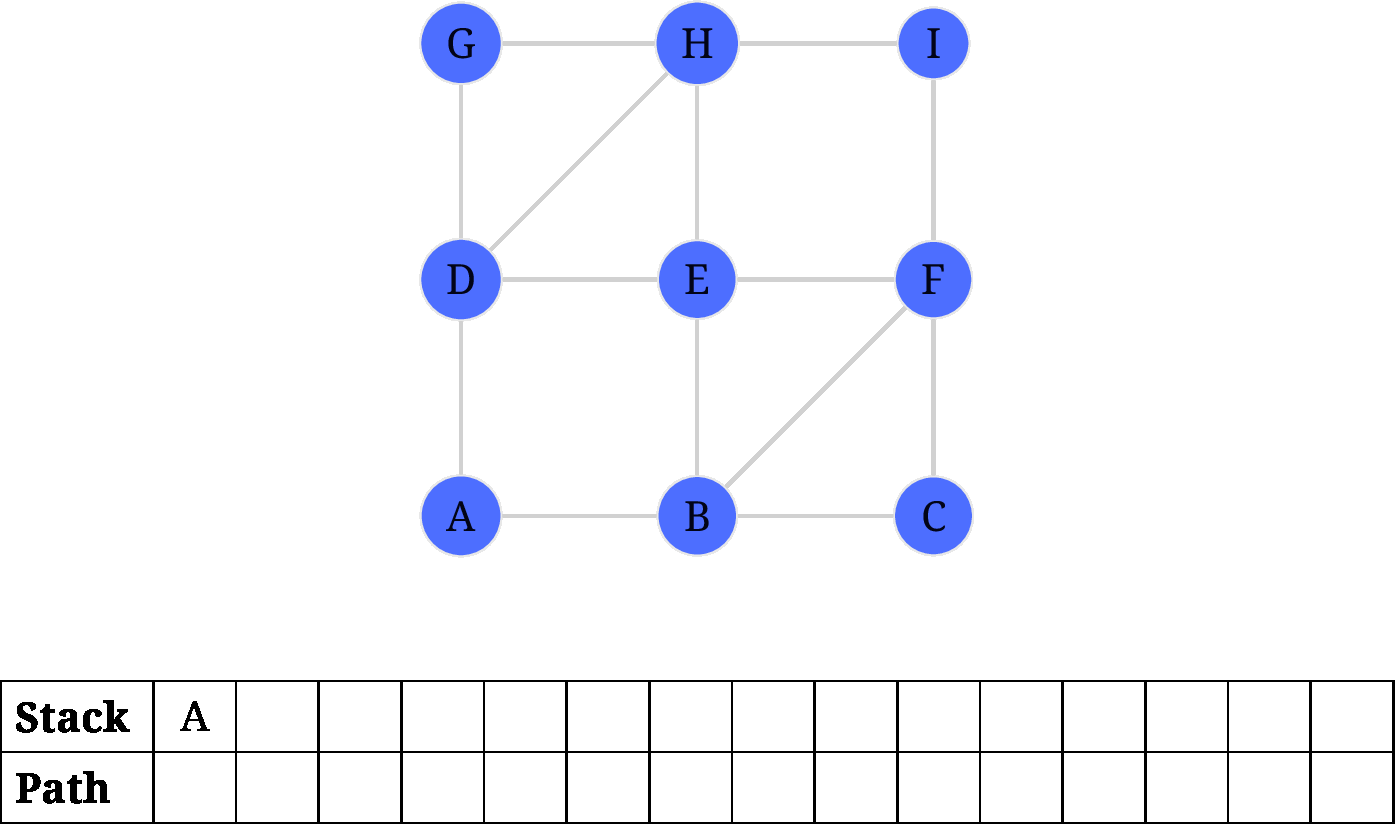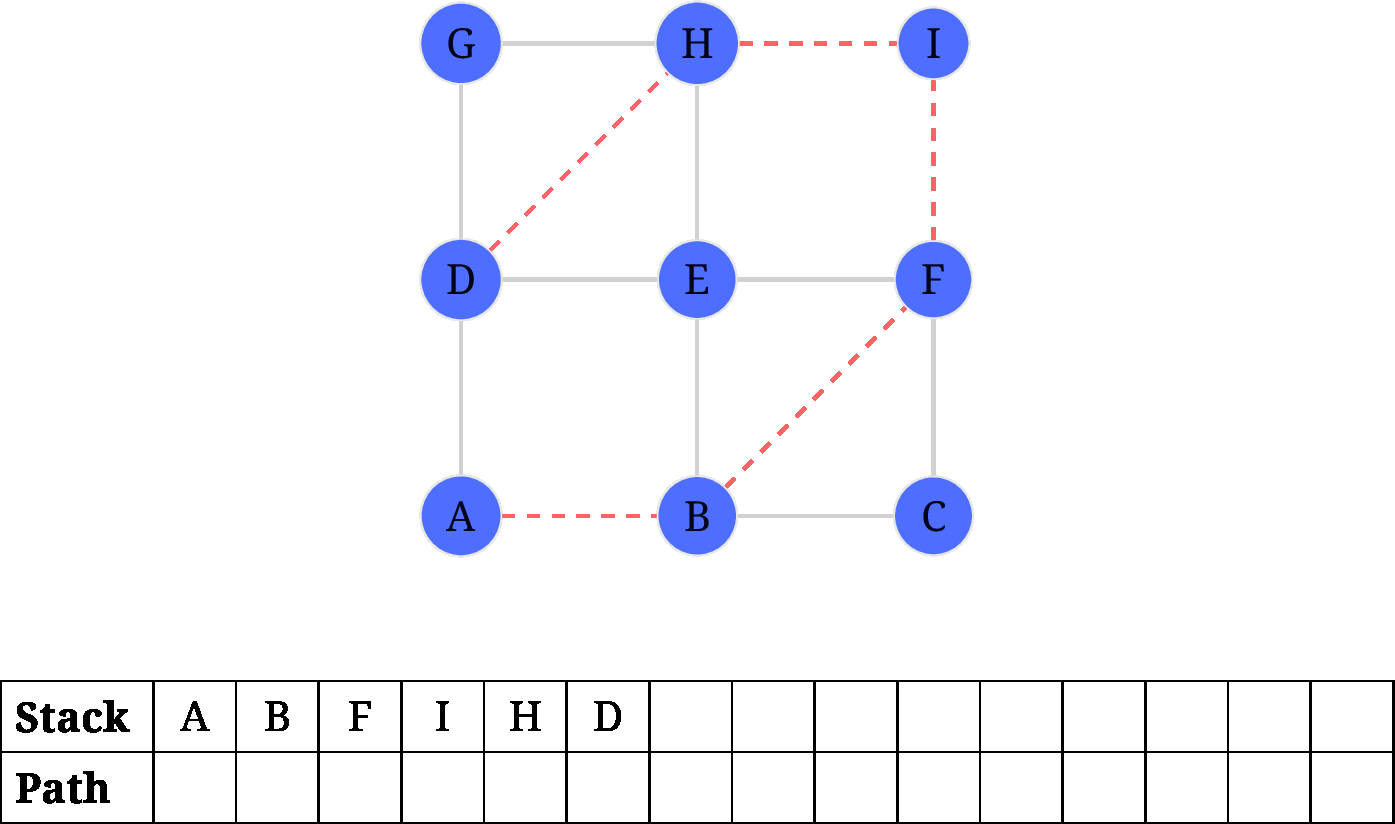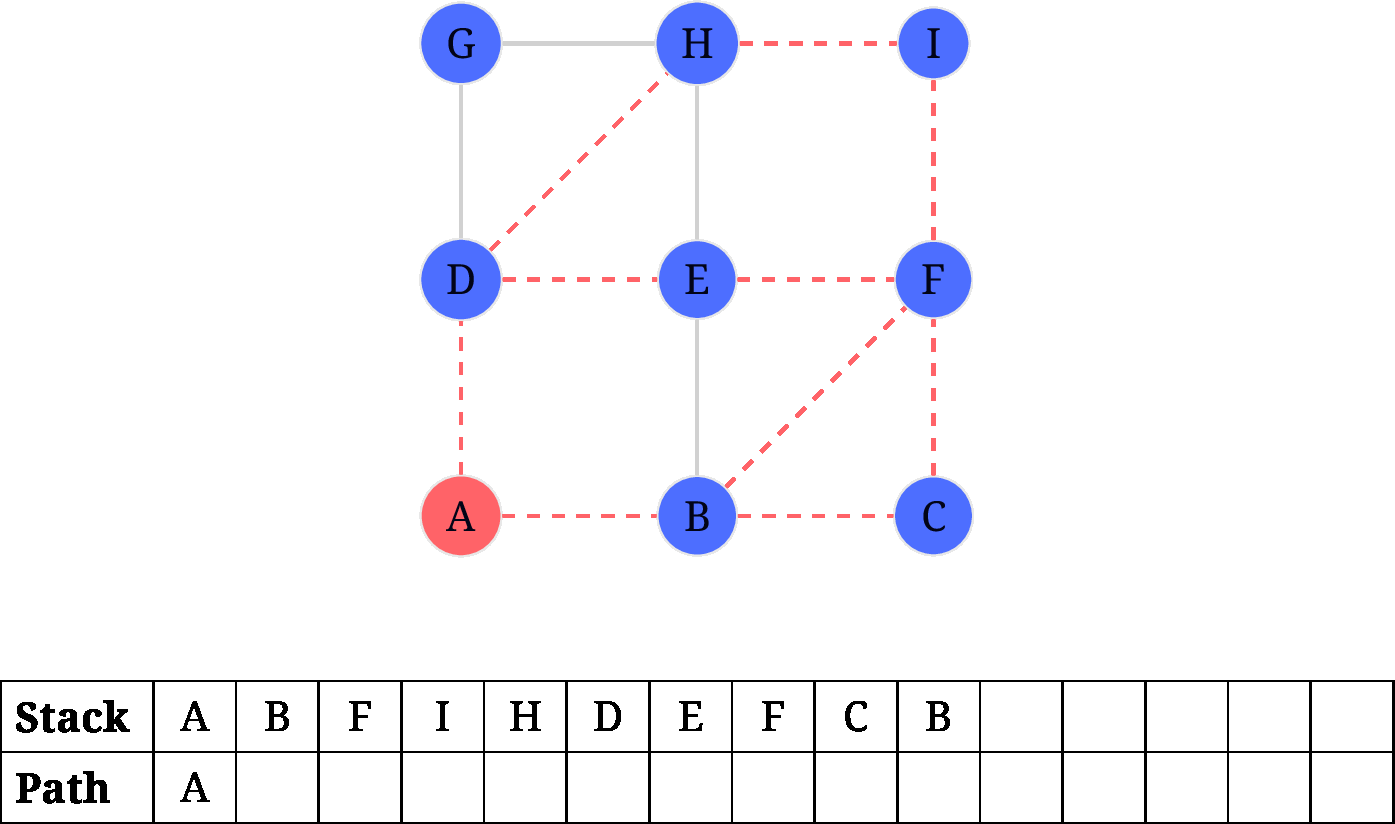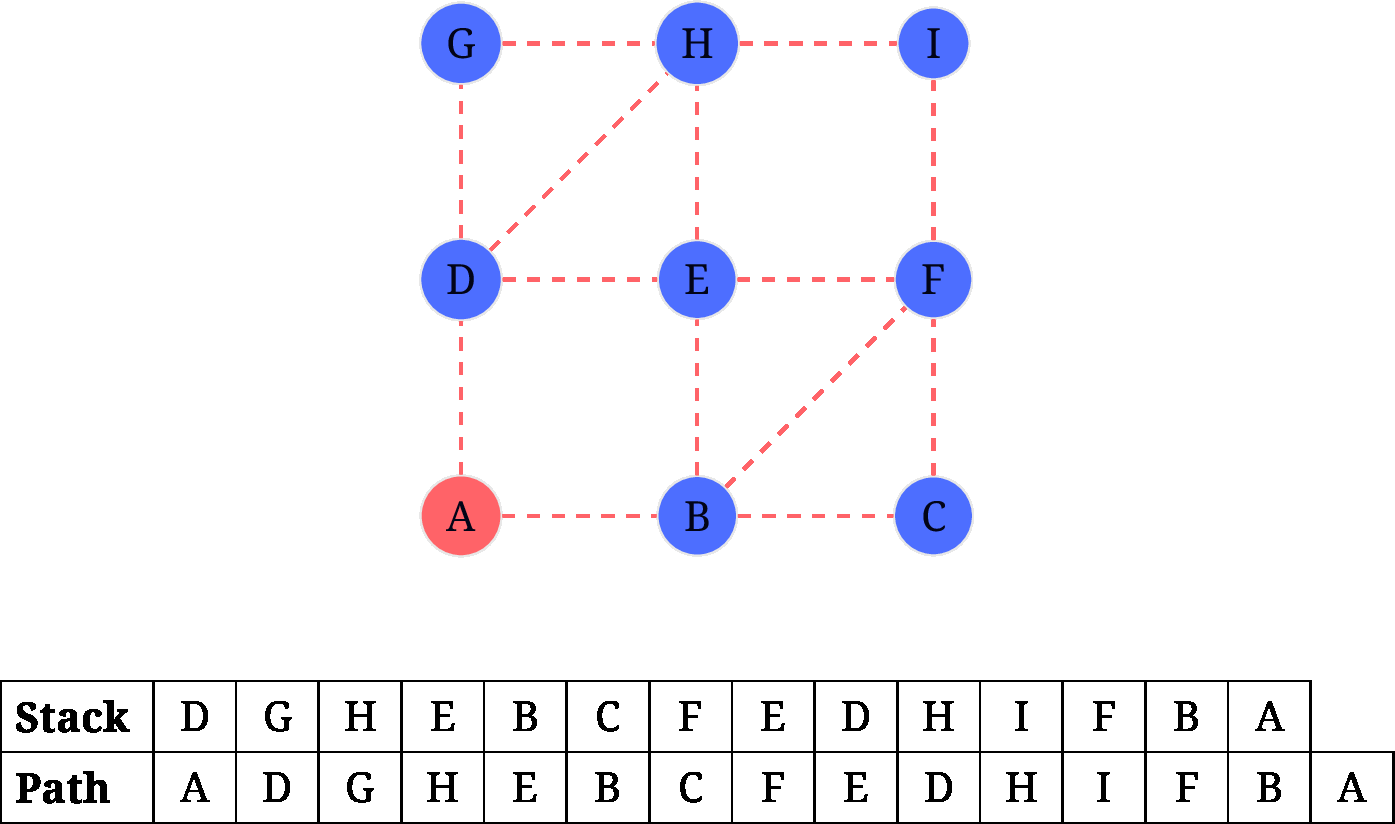
需要注意的是:

当A被第二次访问的时候, 此时没有其他边可走, 因此需要从栈中弹出A并添加到path中.
接下来的出栈操作在所有节点访问完毕的时候.

代码实现

以下是一个具体的 C++ 实现的核心部分, 完整代码请参考:

std::vector<int> FindEulerCircuit(int start) {
  std::stack<int> stack;  // 当前路径
  std::vector<int> path;  // 存储最终的欧拉回路

  stack.push(start);

  while (!stack.empty()) {
    int currV = stack.top();

    // 如果当前顶点有未访问的边
    auto adjList = graph_.Adj(currV);
    if (!adjList.empty()) {
      int nextV = *adjList.begin();
      graph_.RemoveEdge(currV, nextV);
      stack.push(nextV);
    } else {
      // 如果没有未访问的边，则将当前顶点加入电路
      path.push_back(currV);
      stack.pop();
    }
  }

  // 反转电路以获得正确的顺序
  std::reverse(path.begin(), path.end());
  return path;
}
 class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">

欧拉回路与哈密尔顿回路: Fleury算法与Hierholzer 算法(C++)