多源最短路径求解: Floyd-Warshall算法和Johnson 算法

25-03-07 15:01

2549

6233

blog.csdn.net

id="article_content" class="article_content clearfix"> id="content_views" class="markdown_views prism-dracula">

图论相关帖子

环境要求

本文所用样例在Windows 11以及Ubuntu 24.04上面编译通过.

Windows: 使用[Visual Studio],
Ubuntu: 使用 Clang 18.1.3. (Ubuntu 24.04 系统安装版本)
GCC 无法编译直接本项目代码, 因为本文代码使用了 C++20 Module, 而 GCC 对此支持不完整.

Intro

多源最短路径问题是图论中的一个经典问题, 它要求找到图中所有顶点对之间的最短路径. 这个问题可以通过几种不同的算法来解决, 其中最为著名的包括 Floyd-Warshall Algorithm 和 Johnson’s Algorithm.

Floyd-Warshall 算法

弗洛伊德-沃沙尔算法(Floyd-Warshall Algorithm) 是一种用于解决所有顶点对最短路径问题的经典动态规划算法. 它适用于加权图, 包括带有负权重边的图, 但不允许存在负权重环. 该算法的时间复杂度为 $O(V^3)$ , 其中 $V$ 是图中顶点的数量, 因此对于中小规模的完全图或接近完全图特别有效.

算法原理

弗洛伊德-沃沙尔算法的核心思想是逐步尝试通过每个顶点作为中间节点, 更新所有可能的顶点对之间的最短路径估计值. 具体来说, 算法使用一个二维数组 D 来存储顶点间的最短路径长度, 其中 D[i][j] 表示从顶点 i 到顶点 j 的最短路径长度. 初始时, D[i][j]等于图中顶点 i 和 j 之间的直接距离(如果存在), 或者设置为无穷大(如果没有直接连接).

算法的基本步骤如下:

初始化: 根据图的邻接矩阵初始化距离矩阵 D. 如果两个顶点之间没有直接连接, 则将相应的 D[i][j]设为无穷大; 如果 i=j, 则 D[i][i]=0.
迭代更新: 对于每一对顶点(i, j), 考虑每一个顶点 k 作为中间节点, 检查是否可以通过 k 改进 i 到 j 的路径:
- 如果D[i][k] + D[k][j] < D[i][j], 则更新D[i][j] = D[i][k] + D[k][j].
- 这个过程需要遍历所有的顶点对(i, j)以及所有的中间节点 k, 因此时间复杂度为 $O(V^3)$ .
检测负权重环: 在某些应用场景下, 可能还需要检测图中是否存在负权重环. 可以在上述步骤完成后进行一次额外的遍历, 检查是否有任何顶点 i 满足D[i][i] < 0的情况, 如果有, 则说明图中存在负权重环.

样例

给定一个无向带权图, 求任意两个顶点的最短路径.

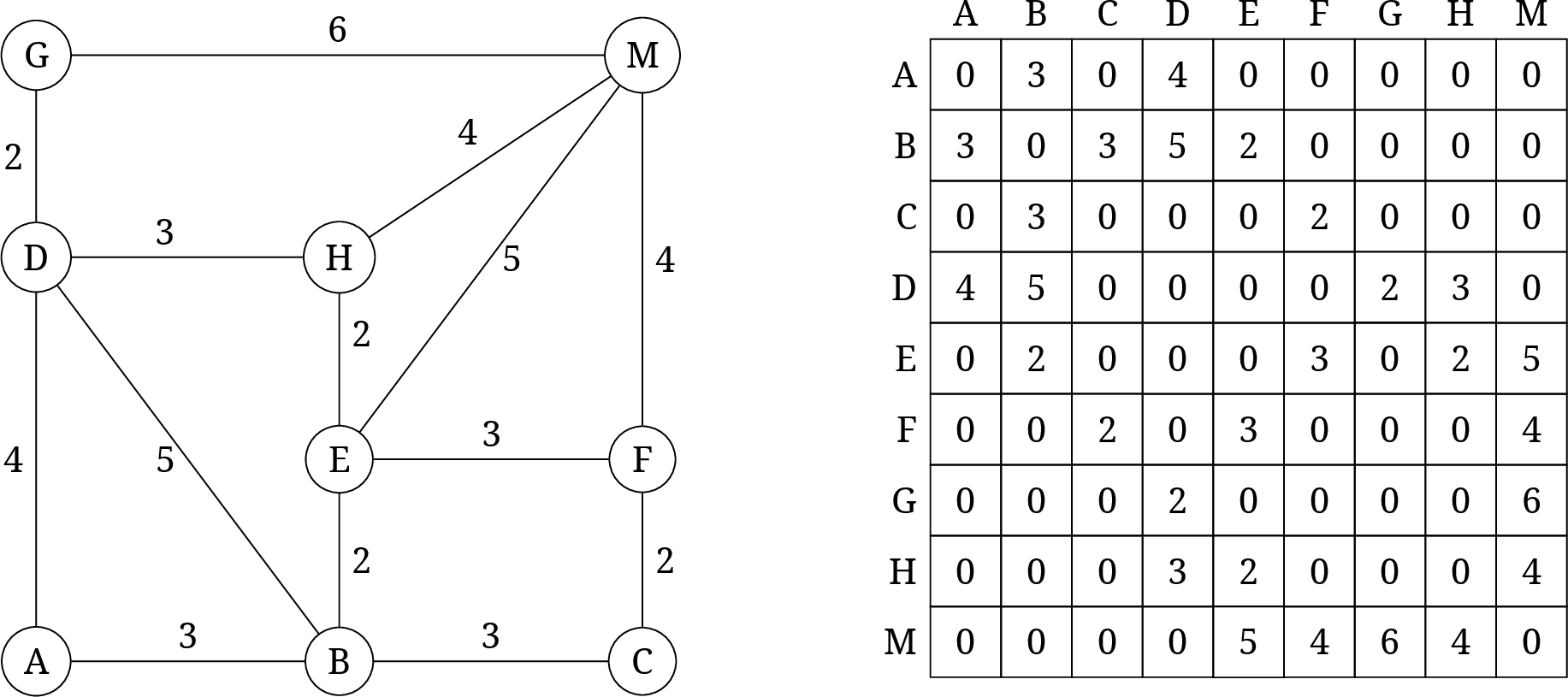
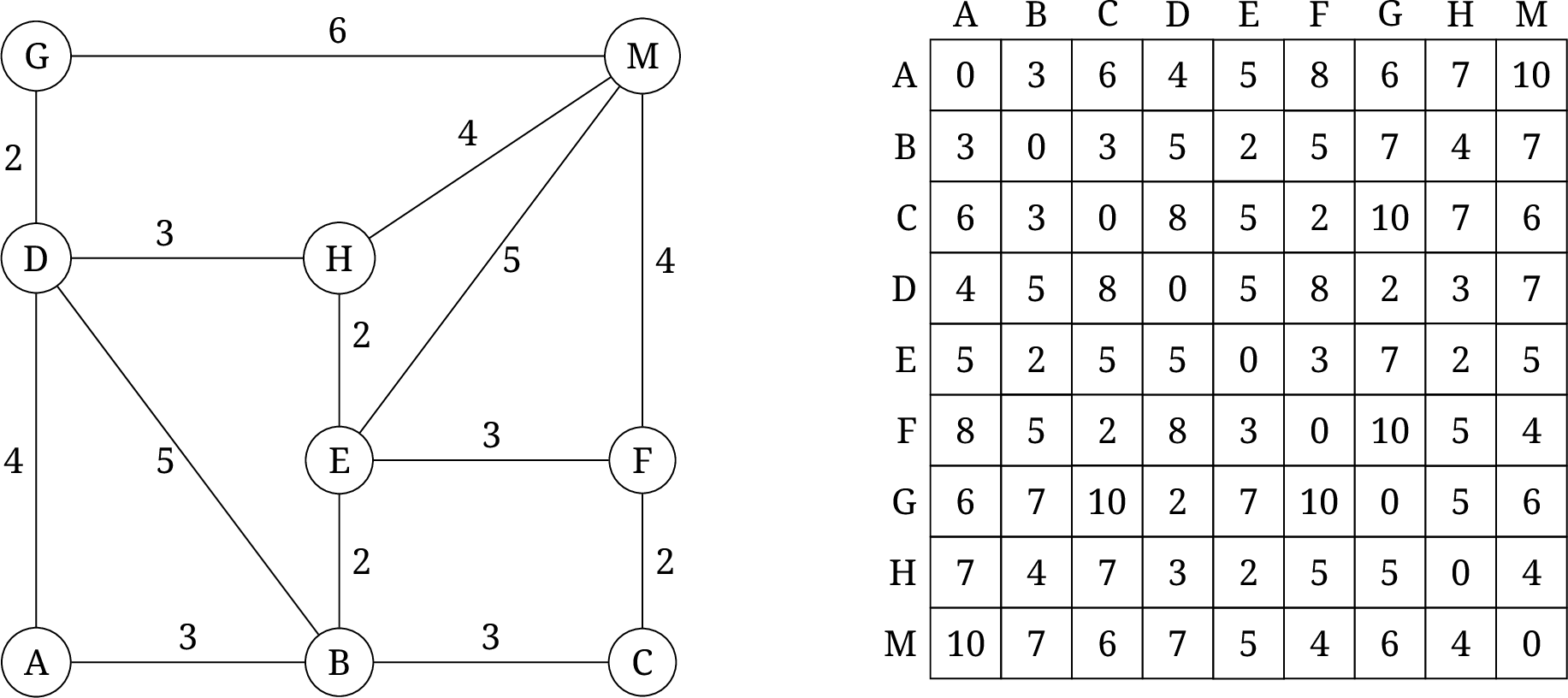
用 Floyd-Warshall 算法解决这个问题. 因为矩阵运算非常直白, 没有分步骤演示的必要, 直接给出结果:

C++实现

算法实现起来非常直白, 下面是核心部分代码:
其中 D 为邻接矩阵, D[i][j] 表示从顶点 i 到顶点 j 的最短路径长度.

void FloydWarshall() {
  auto n = D.size();
  for (int k = 0; k < n; ++k) {
    for (int i = 0; i < n; ++i) {
      for (int j = 0; j < n; ++j) {
        if (D[i][k] + D[k][j] < D[i][j]) {
          D[i][j] = D[i][k] + D[k][j];
        }
      }
    }
  }
}
 class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">

完整代码请参考: FloydWarshall.ixx

时间与空间复杂度

时间复杂度: 由于需要遍历所有顶点对(i, j)以及所有可能的中间节点 k, 因此总的时间复杂度为 $O(V^3)$ .
空间复杂度: 主要由距离矩阵 D 决定, 其大小为 $\times V$ , 因此空间复杂度是 $O(V^2)$ .

Johnson 算法

约翰逊算法(Johnson’s Algorithm) 是一种用于计算加权图中所有顶点对之间最短路径的有效算法. 它特别适用于稀疏图, 即边的数量远小于完全图的边数. 约翰逊算法巧妙地结合了 Bellman-Ford 算法和 Dijkstra 算法的优点, 能够处理带有负权重边但不允许存在负权重环的情况.

算法原理

约翰逊算法的核心思想是通过重新赋予权重, 使得原图中的所有边权重变为非负数, 从而可以利用效率更高的 Dijkstra 算法来解决单源最短路径问题. 具体步骤如下:

添加虚拟节点: 首先, 在原图中添加一个虚拟起点, 并从这个虚拟起点向图中每一个实际存在的节点连接一条权重为 0 的边.
执行 Bellman-Ford 算法: 使用 Bellman-Ford 算法从虚拟起点出发, 计算出每个节点的最小偏移值 $h (v)$ . 这里的偏移值 $h (v)$ 表示的是从虚拟起点到节点 $v$ 的最短路径长度. 这一步骤不仅能够检测图中是否存在负权重环, 而且还能为后续步骤提供必要的偏移值.
重新赋予权重: 对于每条边 $(u, v)$ , 其新的权重 $w^{'} (u, v) = w (u, v) + h (u) - h (v)$ . 这里, $w (u, v)$ 是原图中边 $(u, v)$ 的权重, 而 $h (u)$ 和 $h (v)$ 分别是节点 $u$ 和 $v$ 的偏移值. 这样做的目的是为了消除原图中的负权重边, 同时保证最短路径不会因此发生改变.
运行 Dijkstra 算法: 对于每个节点作为源节点, 分别运行一次 Dijkstra 算法, 以求解该源节点到其它所有节点的最短路径. 由于经过重新赋予权重后所有的边权重都变成了非负数, 所以可以高效地应用 Dijkstra 算法.
调整最短路径长度: 最后, 根据每个节点的偏移值调整最终的最短路径长度, 恢复原始图中的真实最短路径长度.

关于 Bellman-Ford 和 Dijkstra 算法, 请参考: 图的最短路径:Dijkstra 算法和 Bellman-Ford 算法(C++)

时间复杂度

假设图中有 $V$ 个顶点和 $E$ 条边, 约翰逊算法的时间复杂度主要由两部分组成:

Bellman-Ford 算法的时间复杂度为 $O (V E)$ .
对于每个顶点分别运行一次 Dijkstra 算法, 总时间复杂度为 $\log V))$ , 其中使用斐波那契堆实现的 Dijkstra 算法的时间复杂度为 $O (E + V l o g V)$ .

因此, 整个约翰逊算法的时间复杂度大约为 $O(V^2 log V + VE)$ , 在稀疏图上表现尤为出色.

算法对比

下面是约翰逊算法（Johnson’s Algorithm）和弗洛伊德-沃沙尔算法（Floyd-Warshall Algorithm）在不同方面的对比表格。这个表格可以帮助你更好地理解两种算法的特点、适用场景及其优缺点。

class="table-box">

特性/指标	约翰逊算法 (Johnson’s Algorithm)	弗洛伊德-沃沙尔算法 (Floyd-Warshall Algorithm)
处理负权重边	支持，通过重新赋予权重消除负权重边	支持，直接处理负权重边
处理负权重环	通过贝尔曼-福特算法检测并排除	可以检测到负权重环
时间复杂度	$O(V^2 log V + VE)$	$O(V^3)$ ，适用于中小规模的完全图或接近完全图
空间复杂度	$O(V^2)$ ，主要用于存储距离矩阵和优先队列	$O(V^2)$ ，主要用于存储距离矩阵
适用场景	适用于大规模稀疏图，尤其是当图中存在负权重边但无负权重环时	适用于中小规模稠密图，或者需要快速解决所有顶点对最短路径问题时
典型应用场景	社交网络分析、交通网络优化、大规模稀疏图中的最短路径计算	图形学中的碰撞检测、机器人路径规划、电路设计中的布线优化

图论相关帖子

环境要求

Intro

Floyd-Warshall 算法

算法原理

样例

C++实现

时间与空间复杂度

Johnson 算法

算法原理

时间复杂度

算法对比

评论记录：