上文中我们了解了拓扑排序, 本节我们来学习最短路径的算法.
在图论中, 最短路径问题是指在一个加权图中找到两个节点之间的权重和最小的路径.
最短路径问题是一个基础且重要的主题. 它不仅在理论上具有挑战性, 而且在实际应用中也非常广泛, 比如交通导航, 社交网络分析等. 本文将介绍几种解决最短路径问题的经典算法, 并讨论它们的应用场景.
环境要求
本文所用样例在Windows 11以及Ubuntu 24.04上面编译通过.
- Windows: 使用[Visual Studio],
- Ubuntu: 使用 Clang 18.1.3. (Ubuntu 24.04 系统安装版本)
- GCC 无法编译直接本项目代码, 因为本文代码使用了 C++20 Module, 而 GCC 对此支持不完整.
关于 Module 的更多信息, 请参考我之前的博客: CMake 构建 C++20 Module 实例(使用 MSVC)
本项目工程目录: 图论代码
1. Dijkstra 算法
Dijkstra 算法是由荷兰计算机科学家艾兹赫尔·戴克斯特拉(Edsger W. Dijkstra)于 1956 年提出的一种用于解决加权图中单源最短路径问题的算法. 该算法适用于所有边权重为非负数的情况, 能够找到从一个起点到图中所有其他顶点的最短路径.
核心思想
Dijkstra 算法基于贪心策略, 其核心思想是: 每次从未确定的节点集合中选择距离起点最近的节点作为当前处理对象, 并更新通过该节点到达其他节点的距离估计值. 重复此过程直到所有节点都被处理过, 或者找到了目标节点.
算法步骤
以下是 Dijkstra 算法的基本步骤:
-
初始化:
- 将起始节点的距离设为 0, 其余所有节点的距离设为无穷大.
- 创建一个优先队列(或最小堆), 将所有节点加入其中, 起始节点的优先级最高(即距离最小).
-
主循环:
- 从优先队列中取出距离最小的节点 u.
- 对于节点 u 的每一个邻居 v:
- 计算从起始节点经过 u 到达 v 的距离 d = 距离[u] + 权重(u, v).
- 如果 d 小于当前记录的 v 的距离, 则更新 v 的距离, 并设置 v 的前驱节点为 u.
- 更新优先队列中的 v 节点信息(如果使用的是优先队列).
-
终止条件:
- 当优先队列为空时, 算法结束.
- 或者在找到特定的目标节点后提前终止.
示例
假设我们有一个如下所示的简单无向图:
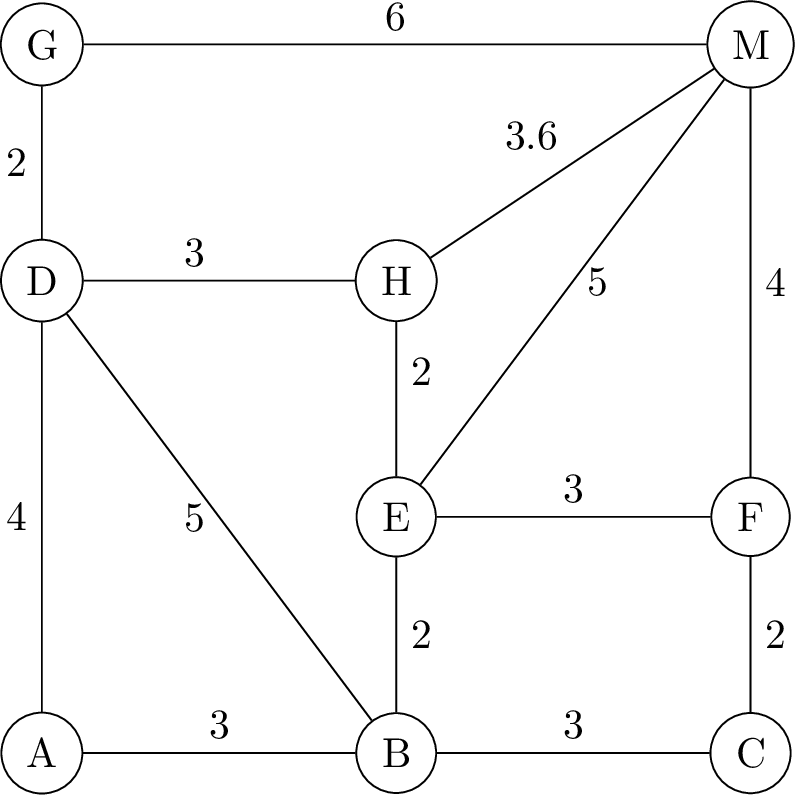
如果我们想找出从 A 到 F 的最短路径, 按照 Dijkstra 算法步骤执行如下:
-
初始化: dist[A]=0, dist[B]=dist[C]=dist[D]=dist[E]=dist[F]=dist[G]=dist[H]=dist[M]= ∞ \infty ∞.
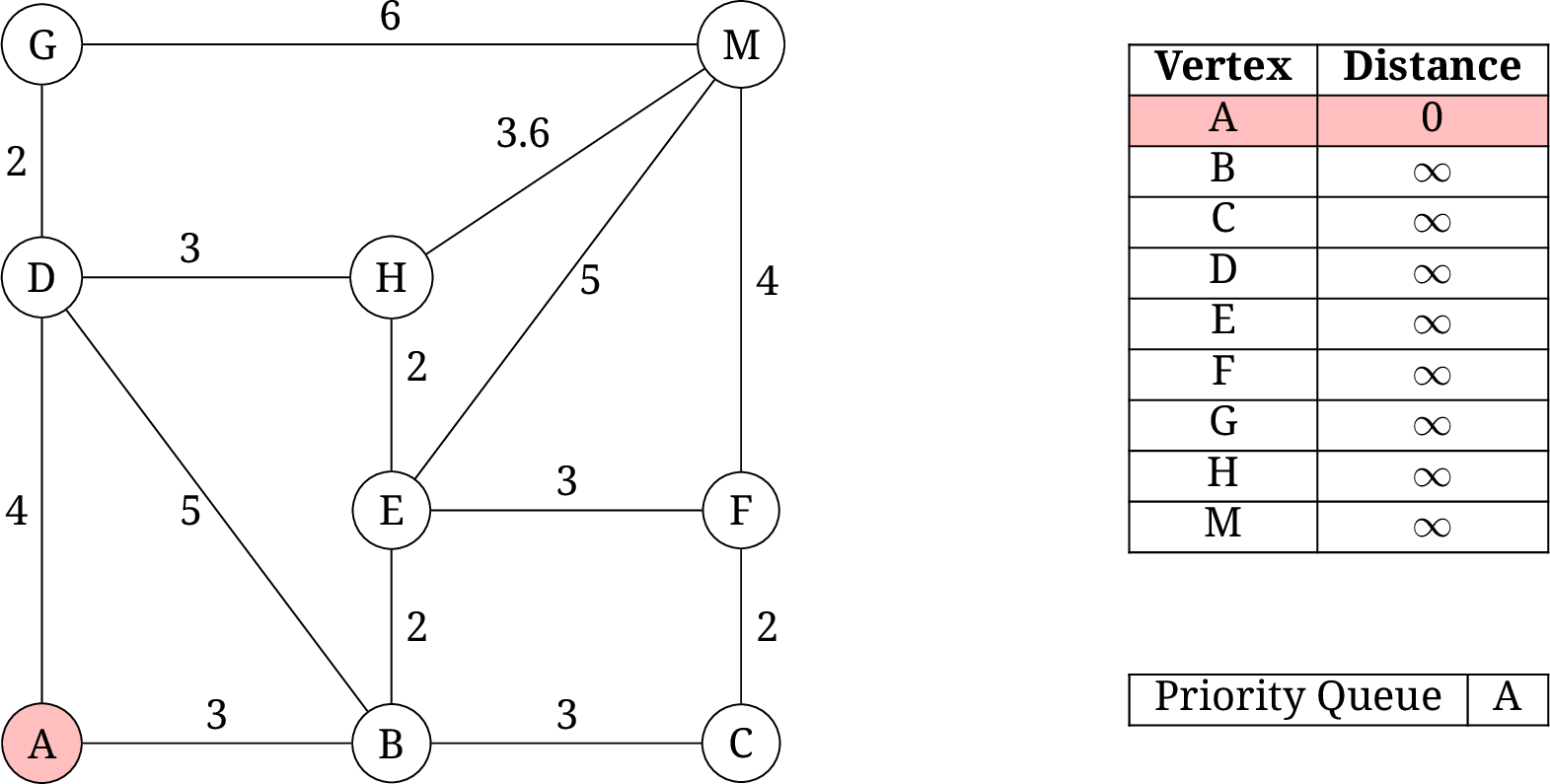
-
主循环:
- 取出
A, 更新B和D的距离为 3 和 4. 下一个要弹出的元素是B.
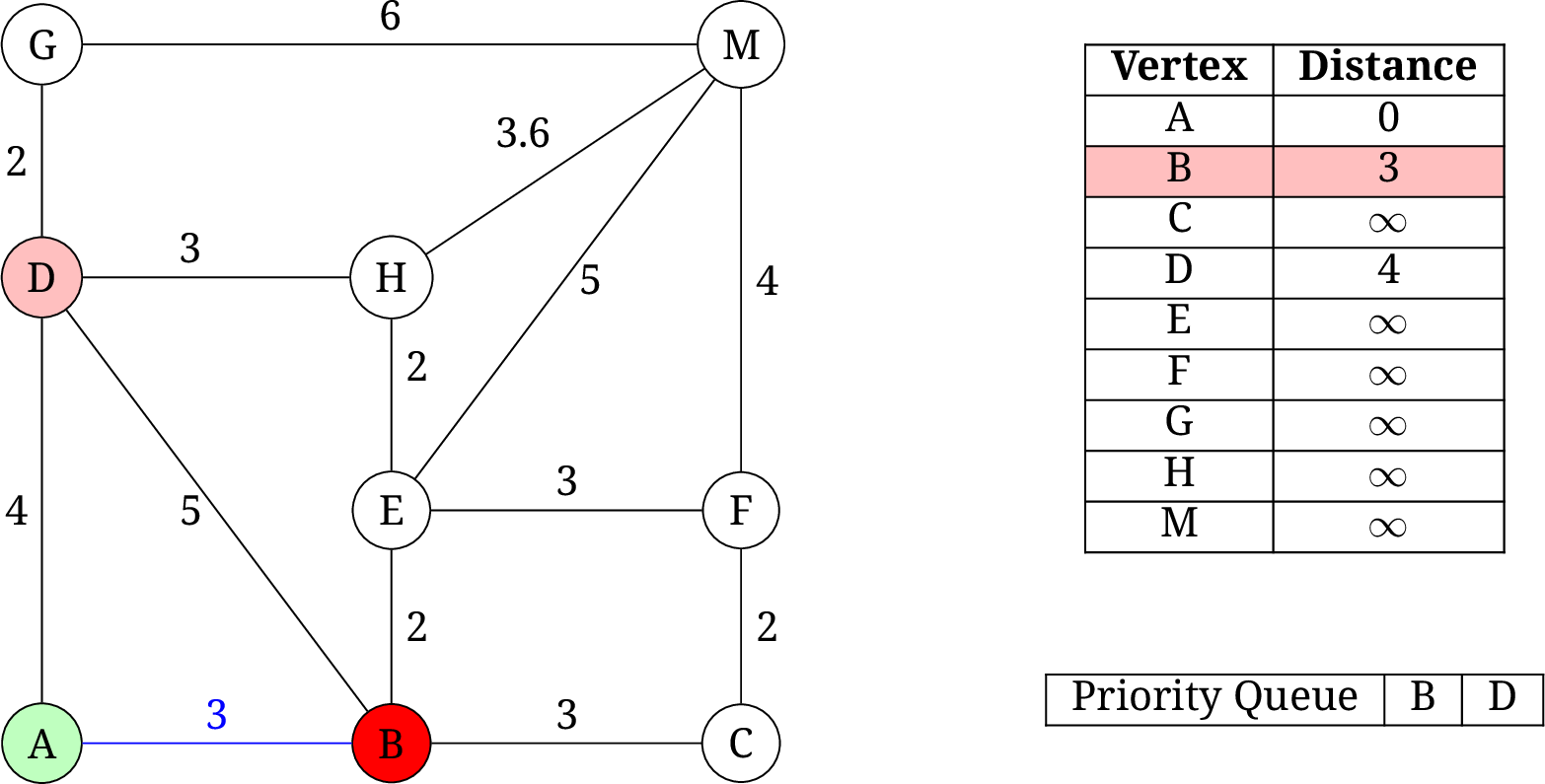
- 取出
B, 更新C和E的距离为 6 和 5. 下一个要弹出的元素是D.
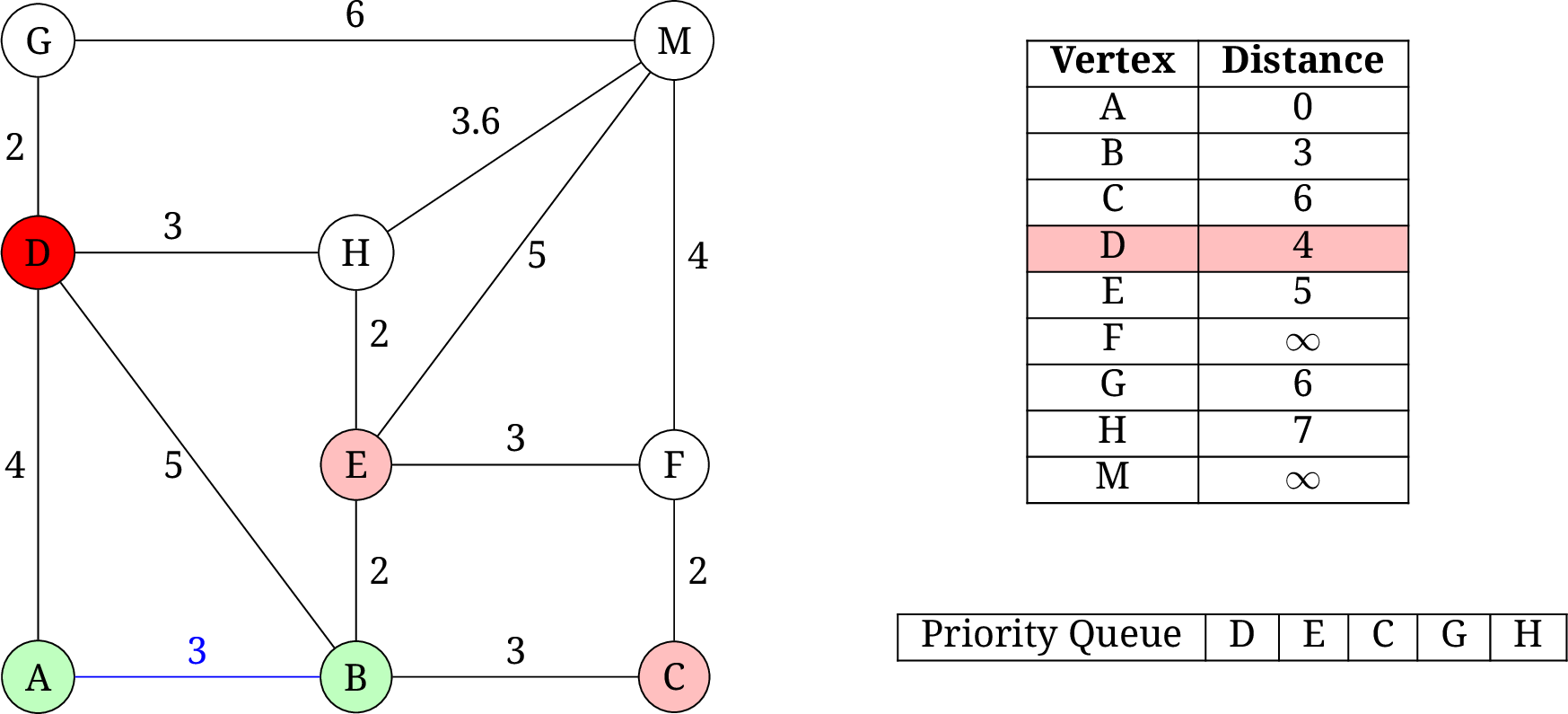
- 取出
D, 更新G和H的距离为 6 和 7. 下一个要弹出的元素是E.
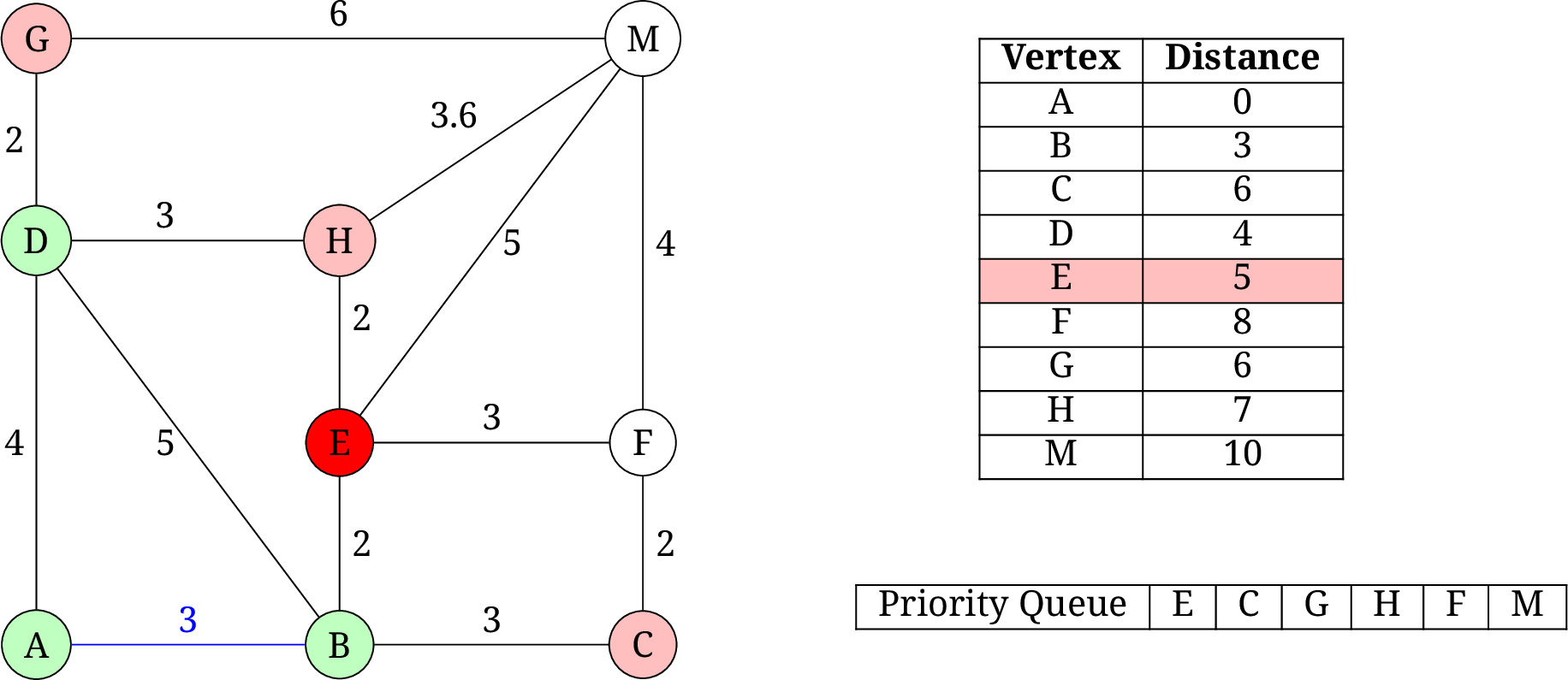
- 取出
E, 更新F和M的距离为 8 和 10. 因为已经到达M, 所以算法结束. 最短距离为 10.
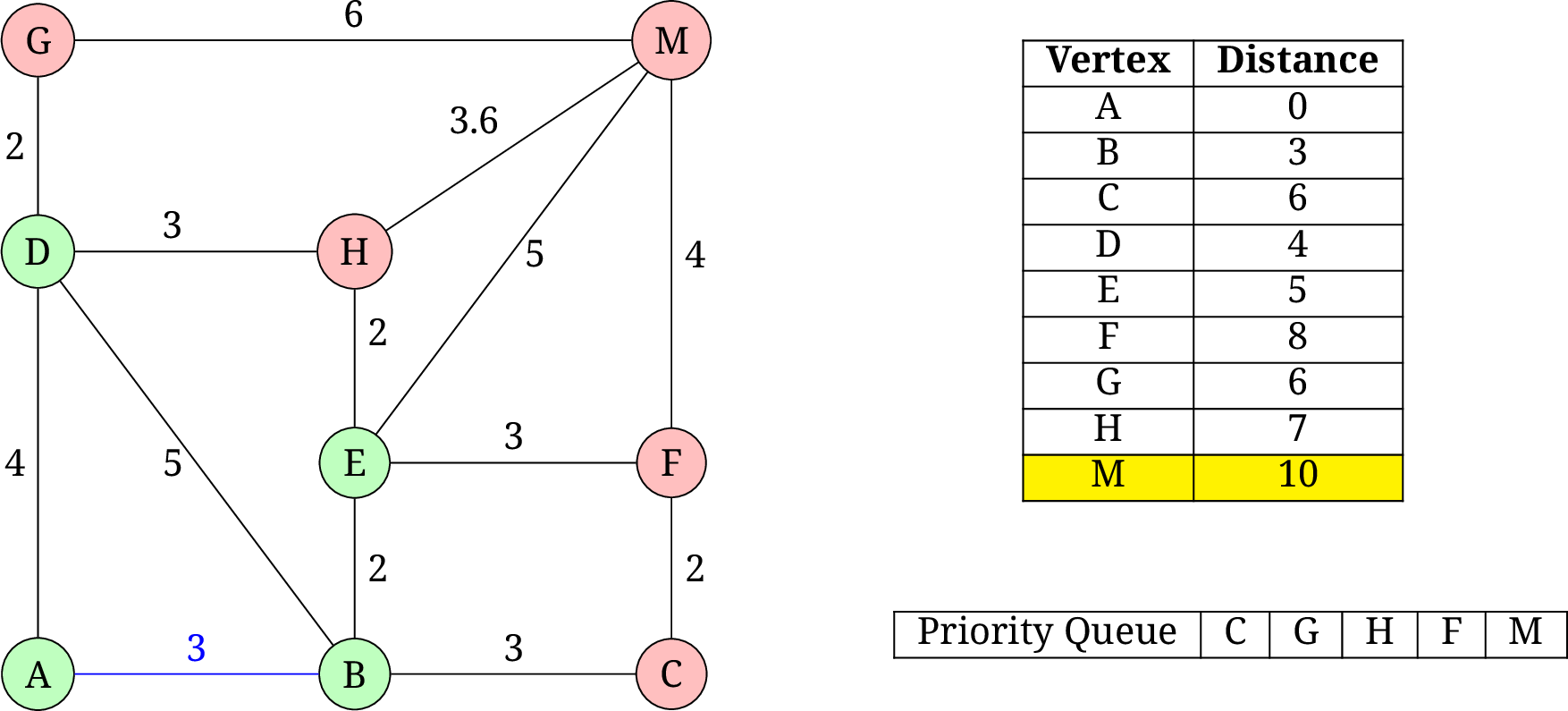
- 取出
时间复杂度
使用优先队列优化的版本时间复杂度为 O ( ( V + E ) log ( V ) ) O((V+E)\log(V)) O((V+E)log(V)), 其中 V V V 是顶点数量, E E E 是边的数量.
代码实现
void dijkstra() {
auto cmp = [](const auto& lhs, const auto& rhs) {
return lhs.second > rhs.second;
};
std::priority_queue<std::pair<Vertex, int class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
评论记录:
回复评论: