目录
1,小美的平衡矩阵

【题目描述】
给定一个n*n的矩阵,该矩阵只包含数字0和1。对于 每个i(1<=i<=n),求在该矩阵中,有多少个i*i的区域满足0的个数等于1的个数???
【题目解析】
示例演示:
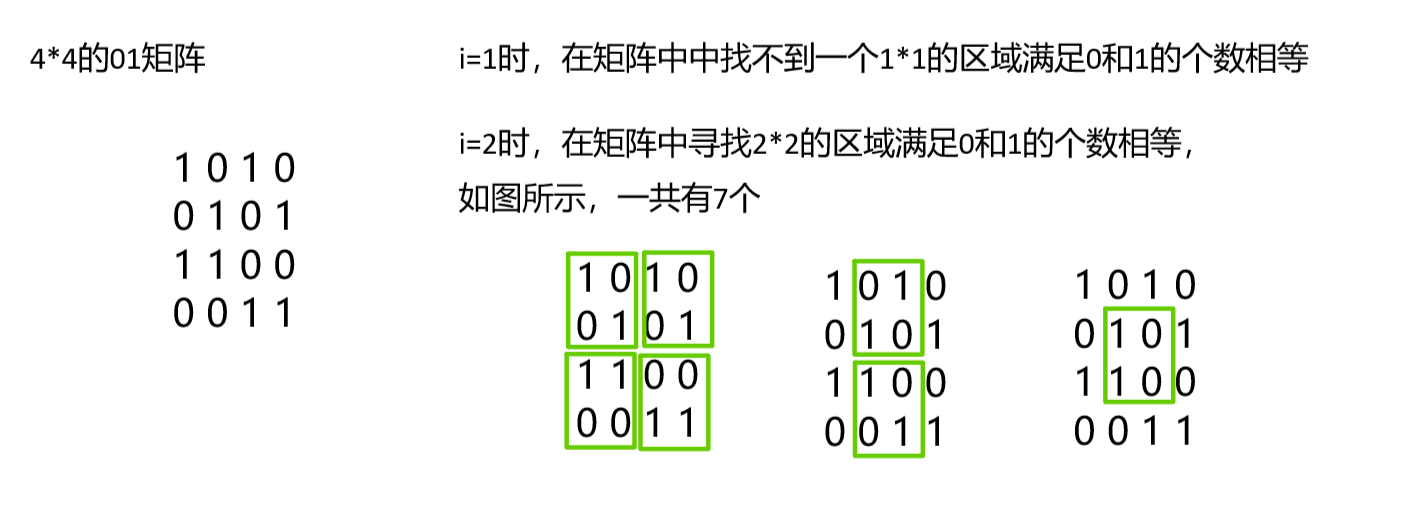
如上图,1*1的区域结果为0,2*2的区域结果为7。
算法:前缀和+遍历
题目中给的数据范围是n<=200,所以可以直接遍历数组。
维护 一个前缀和数组统计以(x,y)这个点为右下角,以(1,1)这个点为左上角,这个区域中所有元素的和,由于数组中的数要么是0,要么是1,所以前缀和就表示某个区域中1的个数。
有了前缀和数组,就可以快速 求出某个区域中1的个数,如图:
而这个区域的大小我们是知道的,假设是k,那么这个区域的元素个数就是k*k。如果满足这个区间中1的个数等于k*k/2,那么说明 这个区间中0和1的个数 相等。而1的个数我们可以通过前缀和来表示。
同时还有一点,如果k为奇数,那么k*k的区域中元素个数一定为奇数 ,所以0和1的个数一定不相等。直接输出0即可。
注意:在输入数据的时候,如果是以整数的形式接受,那么不建议使用cin,因为cin会把第一行的所有数据读成一个整数。就比如 上面的示例,第一行会被读成一个整数1010,而我们期望是读到4个整数的,这是可以使用scanf("%1d",&a),使用 %1d占位符可以确保读到的第一行是4个整数。
【代码】
- #include <iostream>
- #include <vector>
- using namespace std;
-
- const int N = 205;
- int arr[N][N], s[N][N];
- //s为前缀和数组
- //统计矩形(1,1)到(n,n)中1的数量
-
- int main()
- {
- int n = 0;
- cin >> n;
- for(int i=1;i<=n;i++)
- for (int j = 1; j <= n; j++)
- {
- scanf("%1d", &arr[i][j]);
- s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + arr[i][j];
- }
- cout << 0 << endl;
- for (int k = 2; k <= n; k++)
- {
- if (k & 1)
- {
- cout << 0 << endl;
- continue;
- }
- int ans = 0;
- for(int i=1;i+k-1<=n;i++)
- for (int j = 1; j+k-1 <= n; j++)
- {
- //(i,j)是左上角,需要我们计算出k*k这个区域右下角的坐标
- int x = i + k - 1;
- int y = j + k - 1;
- if (s[x][y] - s[i - 1][y] - s[x][j - 1] + s[i - 1][j - 1] == k * k / 2)
- ans++;
- }
- cout << ans << endl;
- }
- return 0;
- }
2,小美的数组询问

直接遍历即可
- #include <iostream>
- using namespace std;
-
- const int N=1e5+10;
- int arr[N];
- int main()
- {
- int n=0,q=0;
- cin>>n>>q;
- long long sum=0,count=0;
- for(int i=1;i<=n;i++)
- {
- cin>>arr[i];
- sum+=arr[i];
- if(arr[i]==0)
- count++;
- }
-
- int l,r;
- while(q--)
- {
- cin>>l>>r;
- cout<<sum+count*l<<" "<<sum+count*r<<endl;
- }
-
- return 0;
- }
3,小美的MT

统计元字符中 有多少个M和T,再加上最多可以修改 多少个即可。
- //小美的MT
- #include <iostream>
- #include <string>
- using namespace std;
-
- int main()
- {
- int n = 0, k = 0;
- cin >> n >> k;
- string str;
- cin >> str;
- int ans = 0;
- for (int i = 0; i < n; i++)
- {
- if (str[i] == 'M' || str[i] == 'T')
- ans++;
- }
- if (k > n - ans)
- cout << n << endl;
- else
- cout << ans + k << endl;
- return 0;
- }
4,小美的朋友关系

【题目描述】
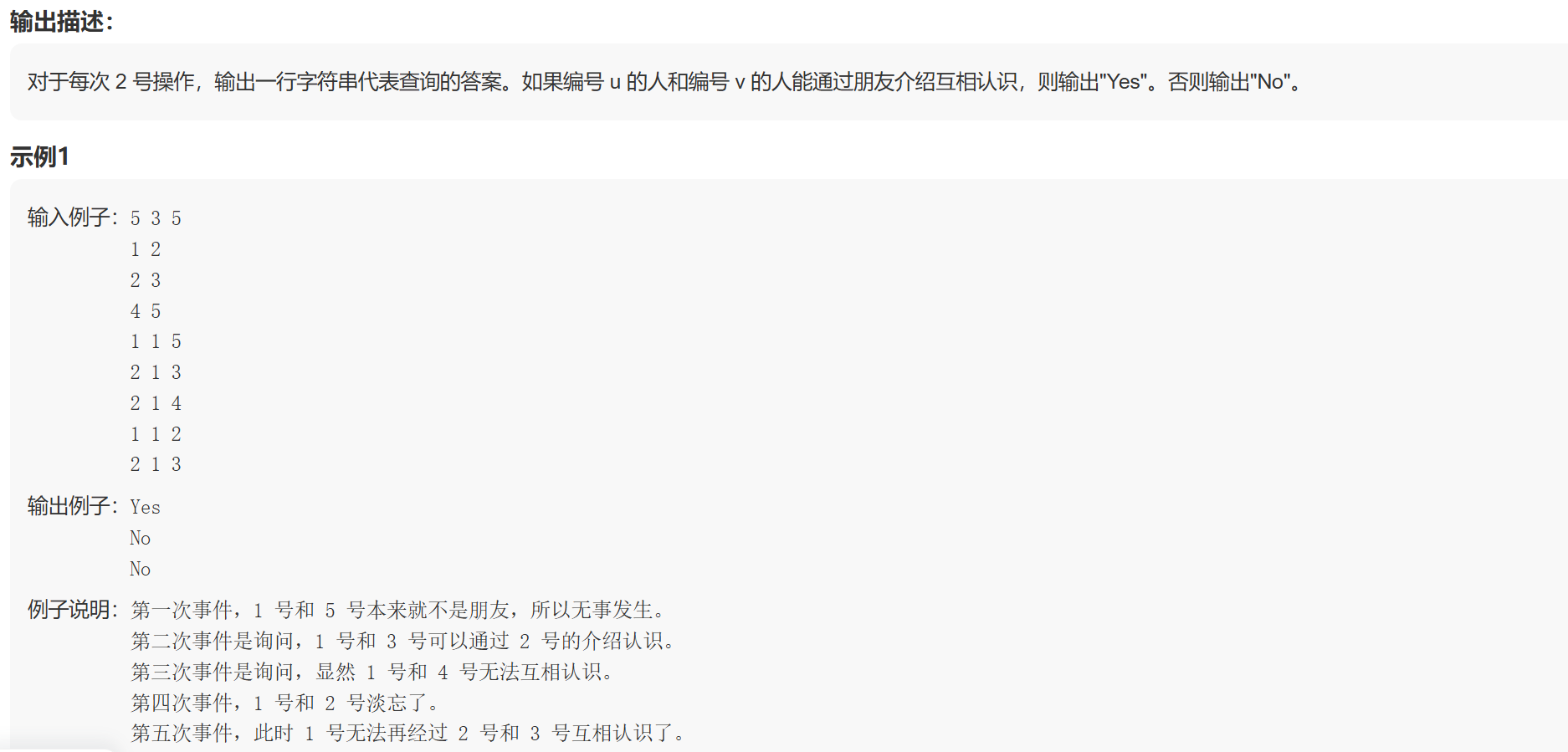
总人数为n,编号u和v的人之间存在朋友关系,在这n个人中,存在m个朋友关系。
对于这些关系,进行q次事件,格式为【op,u,v】,其中u和v表示人的编号。op表示要进行哪种操作,当op==1时,u和v的朋友关系淡忘,也就是断开u和v的朋友关系。当op==2时,表示查询u和v是否可以建立朋友关系,可以通过第三方或者本来就是朋友关系。
针对每次的op==2操作,返回一个结果Yes or No,表示是否可以建立朋友关系 。
【思路】
这n个人中存在许多的朋友关系,比如编号1-5是朋友,编号6-10是朋友,这两个关系是独立的集合,所以可以想到的是使用并查集来记录朋友关系。
并查集传送门:
并查集中的每个集合可以看成是一棵树,独立多个集合,就是多个独立的树。每个树的根节点也就是每个集合的父节点。
刚开始我的思路是将这m个朋友关系,使用并查集来存储。
但是在q次操作中,op=2是查询是否可以 建立朋友关系的操作,这个简单,只需判断这两个人是否在同一个集合中,也就是这两个人的父节点是否相同。但是对于op=1删除朋友关系操作,比较困难,因为并查集擅于进行 添加关系操作的,不好处理删除节点关系。所以在删除朋友关系这里出现了问题。
我们可以试着把删除朋友关系变成添加朋友关系。这样并查集就可以做了。那么怎么实现呢?
我们可以先将这m个朋友关系用特定的容器存储下来,首先遍历q次操作,遇到删除操作(u,v),在容器中删除(u,v)。
注意:这里删除的时候,要删除的朋友关系是(u,v),有可能存储的时候,朋友关系是(u,v),也有可能是(v,u),这些都是要删除的。
遇到op=2时,不进行操作。一次操作完成后,将该次操作用数组记录下来【op,u,v】。
顺序遍历完后,此时将容器中剩余的朋友关系,构建并查集。 然后逆序遍历记录操作的数组,遇到op=1时,就添加朋友关系,遇到op=2时,就查询朋友关系,判断父节点是否相等即可。
【代码】
- //小美的朋友关系
- #include <iostream>
- #include <vector>
- #include <set>
- using namespace std;
- const int N = 1e5;
-
- //总人数,初始的朋友关系数,事件数量
- int n, m, q;
- vector<int> parent;//并查集
- set<pair<int, int>> st;//存储初始的朋友关系
- //存储事件
- struct node
- {
- int op, u, v;
- }arr[N+5];
- //找父节点,路径压缩
- int find(int x)
- {
- if (parent[x] != x)
- parent[x] = find(parent[x]);
- return parent[x];
- }
- //合并
- void unite(int x, int y)
- {
- int rootX = find(x);
- int rootY = find(y);
- if (rootX == rootY)
- return;
- parent[rootX] = rootY;
- }
- int main()
- {
- cin >> n >> m >> q;
- //初始化并查集
- parent.resize(n + 1);
- for (int i = 1; i <= n; i++)
- parent[i] = i;
- //存储关系
- int op,u, v;
- while (m--)
- {
- cin >> u >> v;
- st.insert({ u,v });
- }
- int num = 0;
- while (q--)
- {
- cin >> op >> u >> v;
- //处理删除操作
- if (op == 1)
- {
- if (st.find({ u,v }) != st.end())
- st.erase({ u,v });
- else if (st.find({ v,u }) != st.end())
- st.erase({ v,u });
- else
- continue;//说明u和v表示朋友关系,此次删除操作无意义,不需要存储下来
- }
- //记录操作
- arr[num++] = { op,u,v };
- }
- //删除关系完成后,剩余的元素是没有进行操作的
- //构建并查集
- for (auto [u, v] : st)
- unite(u, v);
- vector<bool> ans;//记录最终结果
-
- //逆序遍历操作
- //如果是删除就进行合并
- //如果是查询就进行判断是否在同一个集合
- for (int i = num - 1; i >= 0; i--)
- {
- op = arr[i].op, u = arr[i].u, v = arr[i].v;
- if (op == 1)
- {
- //合并
- unite(u, v);
- }
- else
- {
- //判断
- ans.emplace_back(find(u) == find(v));
- }
- }
-
- for (int i = ans.size() - 1; i >= 0; i--)
- if (ans[i])
- cout << "Yes" << endl;
- else
- cout << "No" << endl;
-
- return 0;
- }
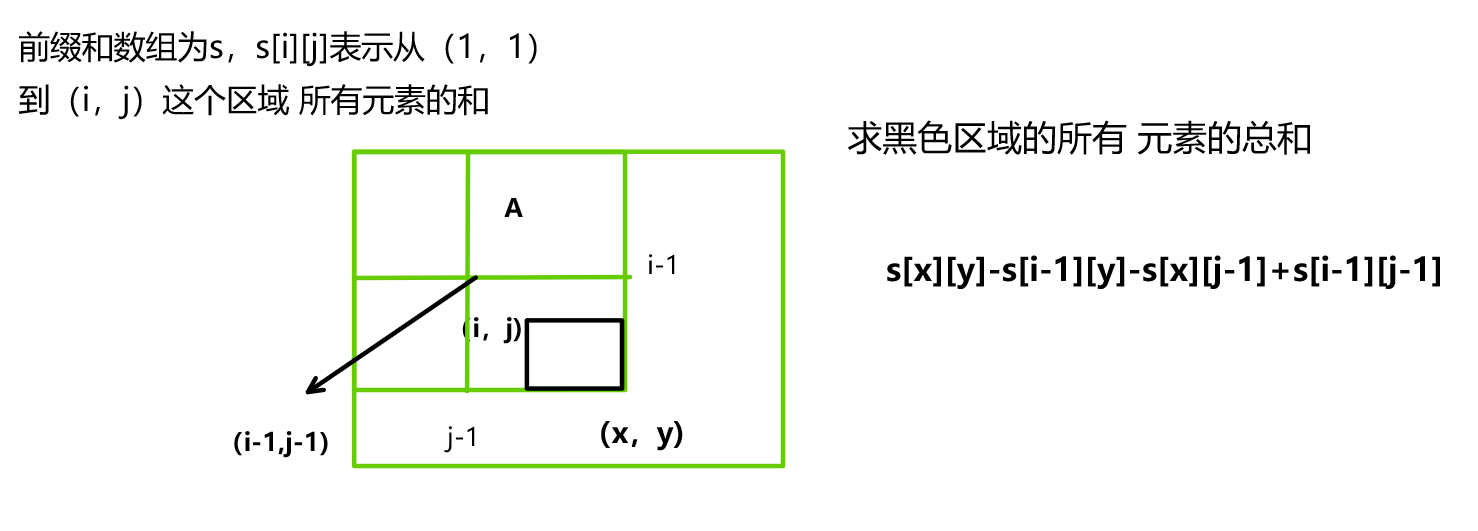
上述代码是使用vector来实现并查集的,题目中的数据范围n是1e9,如果使用vector,就需要开辟1e9个空间,会超出内存限制。所以这里实现并查集的时候,需要使用map来替代。存储当前节点和它的父节点。具体原因,看下方:
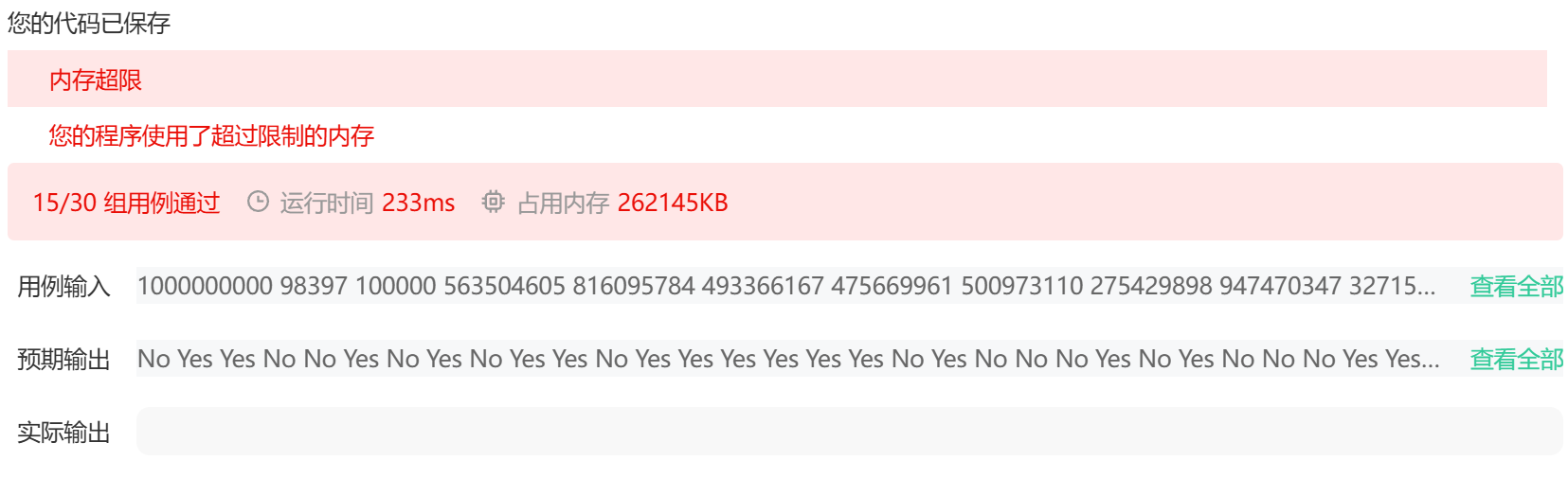
初始时,每个节点的父节点就是自己本身。比如mp[1]=1。
当我们逆序遍历时,当遇到op=2,查询朋友关系时,给的两个朋友编号u和v,之前可能没初始化。比如n=10,给了3个朋友关系(1,3),(3,2),(4,6),当我们查询的时候,可能查询的是(5,7),这两个节点没有初始化,也就是mp[5]=0,mp[7]=0,可以发现这两个节点的父节点都是0,如果直接判断,得到的结果是可以构成朋友关系,但本质是不能构成朋友关系的。
也可以看下方代码的初始化部分,我们只初始化了存在朋友关系的节点,其他的节点没有初始化,他们的父节点默认就是0。如果我们开始将所有节点都初始化好,那么就会超出内存限制,那么就和使用vector一样了,甚至占用的内存比vector还要大,所以我们不能一次性就初始还所有节点。而是当遇到一个没初始化的节点,就初始化即可。
所以在查询操作的时候,如果mp[u]=0,或者mp[v]=0,就把这两个值做一下初始化mp[u]=u或者mp[v]=v,这样在判断的时候就不会出错了。
而如果使用的是vector来表示并查集,是不需要考虑这个问题的,因为vector会开辟n个空间,将所有人都初始化好,父节点就是自己。而使用map来存储,只会存储存在朋友关系的节点,如果出现一个新的节点,需要我们自己再初始化。这也就是map不会超出内存限制而vector会超出内存限制的原因。
【代码】
- //小美的朋友关系
- #include <iostream>
- #include <vector>
- #include <map>
- #include <set>
- using namespace std;
- const int N = 1e5;
-
- //总人数,初始的朋友关系数,事件数量
- int n, m, q;
- map<int,int> parent;//并查集
- set<pair<int, int>> st;//存储初始的朋友关系
- //存储事件
- struct node
- {
- int op, u, v;
- }arr[N + 5];
- //找父节点,路径压缩
- int find(int x)
- {
- if (parent[x] != x)
- parent[x] = find(parent[x]);
- return parent[x];
- }
- //合并
- void unite(int x, int y)
- {
- int rootX = find(x);
- int rootY = find(y);
- if (rootX == rootY)
- return;
- parent[rootX] = rootY;
- }
- int main()
- {
- cin >> n >> m >> q;
- //初始化并查集和关系集合
- int op, u, v;
- for (int i = 0; i < m; i++)
- {
- cin >> u >> v;
- parent[u] = u;
- parent[v] = v;
- st.insert({ u,v });
- }
- int num = 0;
- while (q--)
- {
- cin >> op >> u >> v;
- //处理删除操作
- if (op == 1)
- {
- if (st.find({ u,v }) != st.end())
- st.erase({ u,v });
- else if (st.find({ v,u }) != st.end())
- st.erase({ v,u });
- else
- continue;//说明u和v表示朋友关系,此次删除操作无意义,不需要存储下来
- }
- //记录操作
- arr[num++] = { op,u,v };
- }
- //删除关系完成后,剩余的元素是没有进行操作的
- //构建并查集
- for (auto [u, v] : st)
- unite(u, v);
- vector<bool> ans;//记录最终结果
-
- //逆序遍历操作
- //如果是删除就进行合并
- //如果是查询就进行判断是否在同一个集合
- for (int i = num - 1; i >= 0; i--)
- {
- op = arr[i].op, u = arr[i].u, v = arr[i].v;
- if (op == 1)
- {
- //合并
- unite(u, v);
- }
- else
- {
- //parent[u]==0,说明该节点第一次出现,初始化为u
- if (parent[u] == 0)
- parent[u] = u;
- if (parent[v] == 0)
- parent[v] = v;
- //判断
- ans.emplace_back(find(u) == find(v));
- }
- }
-
- for (int i = ans.size() - 1; i >= 0; i--)
- if (ans[i])
- cout << "Yes" << endl;
- else
- cout << "No" << endl;
-
- return 0;
- }


评论记录:
回复评论: