【算法与数据结构】并查集详解+题目

目录

一，什么是并查集

二，并查集的结构 

三，并查集的代码实现 

1，并查集的大致结构和初始化

2，find操作 

3，Union操作

4，优化 

小结：

四，并查集的应用场景

省份数量[OJ题] 

一，什么是并查集

核心概念：并查集是一种 用于管理元素分组 的数据结构。

在一些应用问题中，需将n个不同的元素划分成一些不相交的集合，开始时，n个元素各自成一个集合，然后按照一定规律将部分集合合成一个集合，也就是集合合并。并查集（union-find)适合来描述这类问题。

对于并查集，我们可以将它看成是一个森林，森林是由多棵树组成的，并查集中的一个个集合就可以看作是树。

示例：

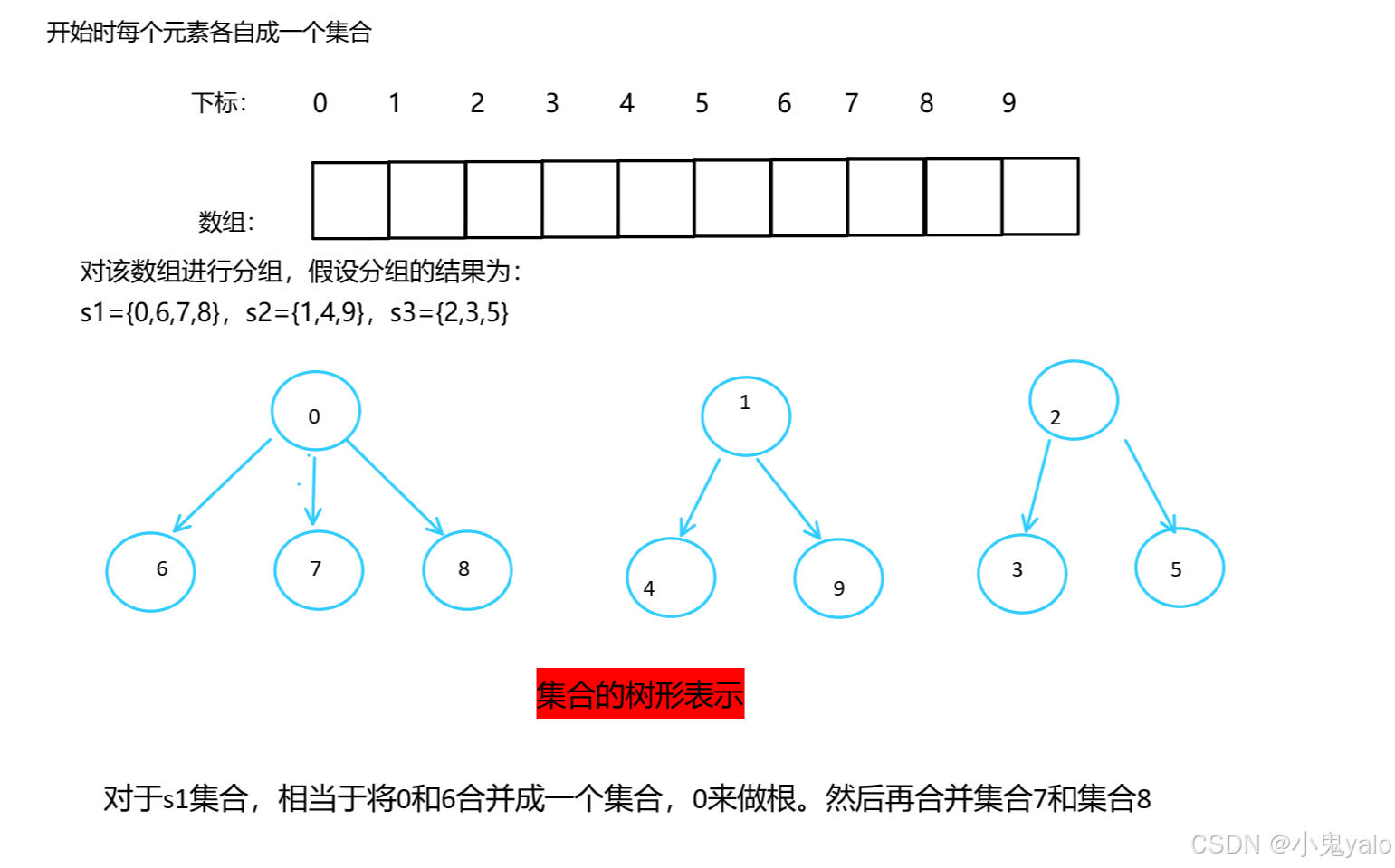
二，并查集的结构 

并查集的存储结构和树的双亲表示法相似。

所谓双亲表示法，就是在树的节点中，只存储父节点的指针，不存储孩子节点的指针。通过指针可以找到父节点。因为对于一颗树来说，可能有多个孩子 ，但只有一个父节点。

 

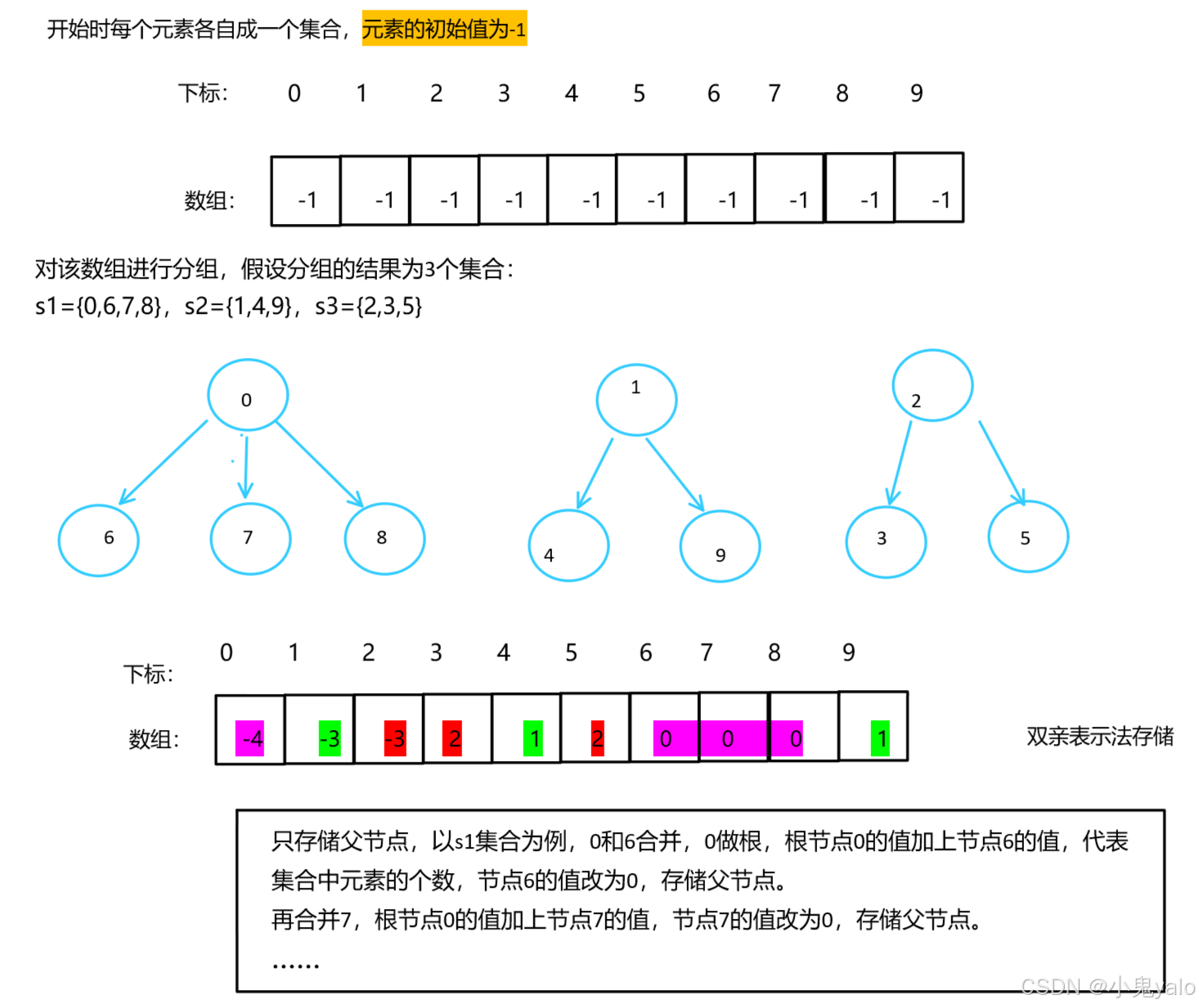
对于上图中：

节点0的数组值为-4，说明该节点为根节点。

节点6的数组值为0，说明该节点的父节点为0。

节点7的数组值为0，说明该节点的父节点为0。

节点8的数组值为0，说明该节点的父节点为0。

三，并查集的代码实现 

并查集主要支持一下操作：

  • 查询（find），查询一个元素在哪个集合中。
  • 合并（union)，将两个集合合并为一个。

1，并查集的大致结构和初始化

class UnionFind
{
public:
    UnionFind(size_t n)
        :_ufs(n,-1)
    {}

    //......
private:
    vector _ufs;
};

2，find操作 

在并查集中找到包含x的根

int findRoot(int x)
{
    int root = x;

    while (_ufs[root] >= 0)
        root = _ufs[root];

    return root;
} 

3，Union操作

合并两个集合

void Union(int x1, int x2)
{
    int root1 = findRoot(x1);
    int root2 = findRoot(x2);
    if (root1 == root2)
        return; //在同一个集合中

    //这里在合并的时候采用数据量小的向数据量大的合并
    //也就是小树向大树合并
    if (abs(_ufs[root1]) < abs(_ufs[root2]))//root1节点更少
    {
        _ufs[root2] += _ufs[root1];
        _ufs[root1] = root2;   //小树合并到大树
    }
    else
    {
        //root2节点更少
        _ufs[root1] += _ufs[root2];
        _ufs[root2] = root1;
    }
}

4，优化 

当树比较高时，我们在反复查某个节点的根节点时，每次都会花费大量时间。

优化方法：路径压缩，只要查找某个节点一次，就将查找路径上的所有节点挂到根节点下面。

如图：查找D的根A，查找路径上包含节点B，将节点D和节点B直接挂在根节点A的下面。

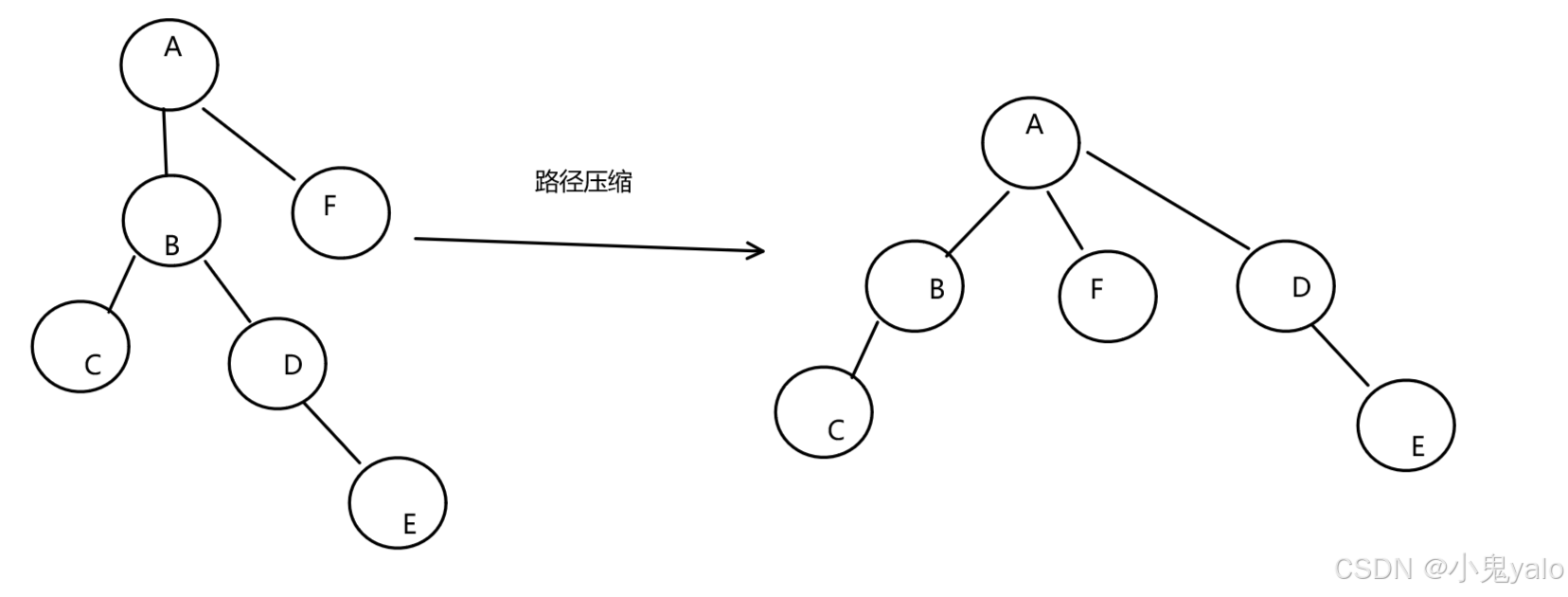
  1. //路径压缩
  2. int findRoot(int x)
  3. {
  4.     int root = x;
  5.  
  6.     while (_ufs[root] >= 0)
  7.         root = _ufs[root];
  8.  
  9.     //路径压缩
  10.     while (_ufs[x] >= 0)
  11.     {
  12.         int parent = _ufs[x];
  13.         _ufs[x] = root;   //挂在根节点的下面
  14.         x = parent;
  15.     }
  16.  
  17.     return root;
  18. }

小结：

上述实现的并查集，支持连续元素。如果是处理非连续元素，需要使用哈希表代替数组（需额处理元素与索引的映射）。

核心思路：

  • 哈希映射：用unordered_map将任意类型元素映射为连续整数ID，内部用数组管理父节点

  • 动态扩容：自动添加新元素，无需预先指定规模。

  • 模板化：支持泛型数据类型（如string等）。

四，并查集的应用场景

  1. 连通性检测：判断网络中两个节点是否连通。

  2. 最小生成树（Kruskal算法）：动态合并边，避免环。

  3. 社交网络分组：快速合并好友关系，查询是否属于同一社交圈。

总结：

并查集通过高效的查找与合并操作，成为处理动态连通性问题的核心数据结构。其优化方法（路径压缩、按秩合并）确保了接近常数的单次操作时间复杂度，适用于大规模数据场景。

其中的按秩合并就是合并集合时小树向大树合并。

省份数量[OJ题] 

题目链接：LCR 116. 省份数量 - 力扣（LeetCode）

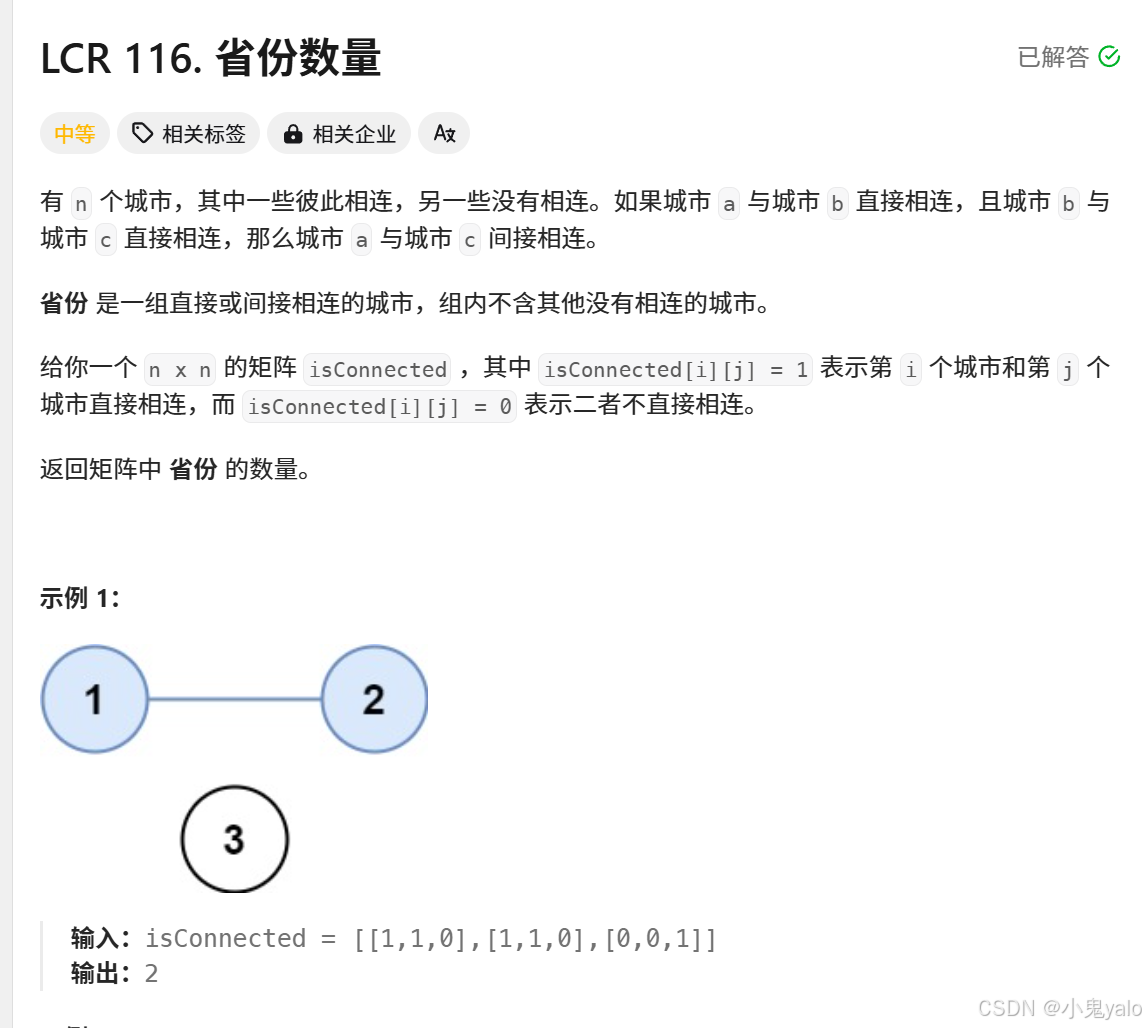
 isConnected[i][j]=1，表示城市i和j连通，连通的城市为一个省份。用并查集将连通的数据放入一个集合，再统计最后的集合个数即可。

  1. class Solution {
  2. public:
  3.     int findCircleNum(vector<vector<int>>& isConnected) {
  4.         int n=isConnected.size();
  5.         vector<int> _ufs(n,-1);
  6.         
  7.         //查找根
  8.         auto find=[&](int x)->int
  9.         {
  10.             int root=x;
  11.             while(_ufs[root]>=0)
  12.             root=_ufs[root];
  13.  
  14.             return root;
  15.         };
  16.  
  17.         for(int i=0;i<n;i++)
  18.         for(int j=0;j<n;j++)
  19.         {
  20.             if(isConnected[i][j]==1)
  21.             {
  22.                 //合并i和j集合
  23.                 int rooti=find(i),rootj=find(j);
  24.                 if(rooti!=rootj)
  25.                 {
  26.                     _ufs[rooti]+=_ufs[rootj];
  27.                     _ufs[rootj]=rooti;
  28.                 }
  29.             }
  30.         }
  31.         //统计集合数
  32.         int ret=0;
  33.         for(auto x:_ufs)
  34.         {
  35.             if(x<0)
  36.             ret++;
  37.         }
  38.  
  39.         return ret;
  40.     }
  41. };

冗余连接[OJ题]

题目链接：684. 冗余连接 - 力扣（LeetCode）

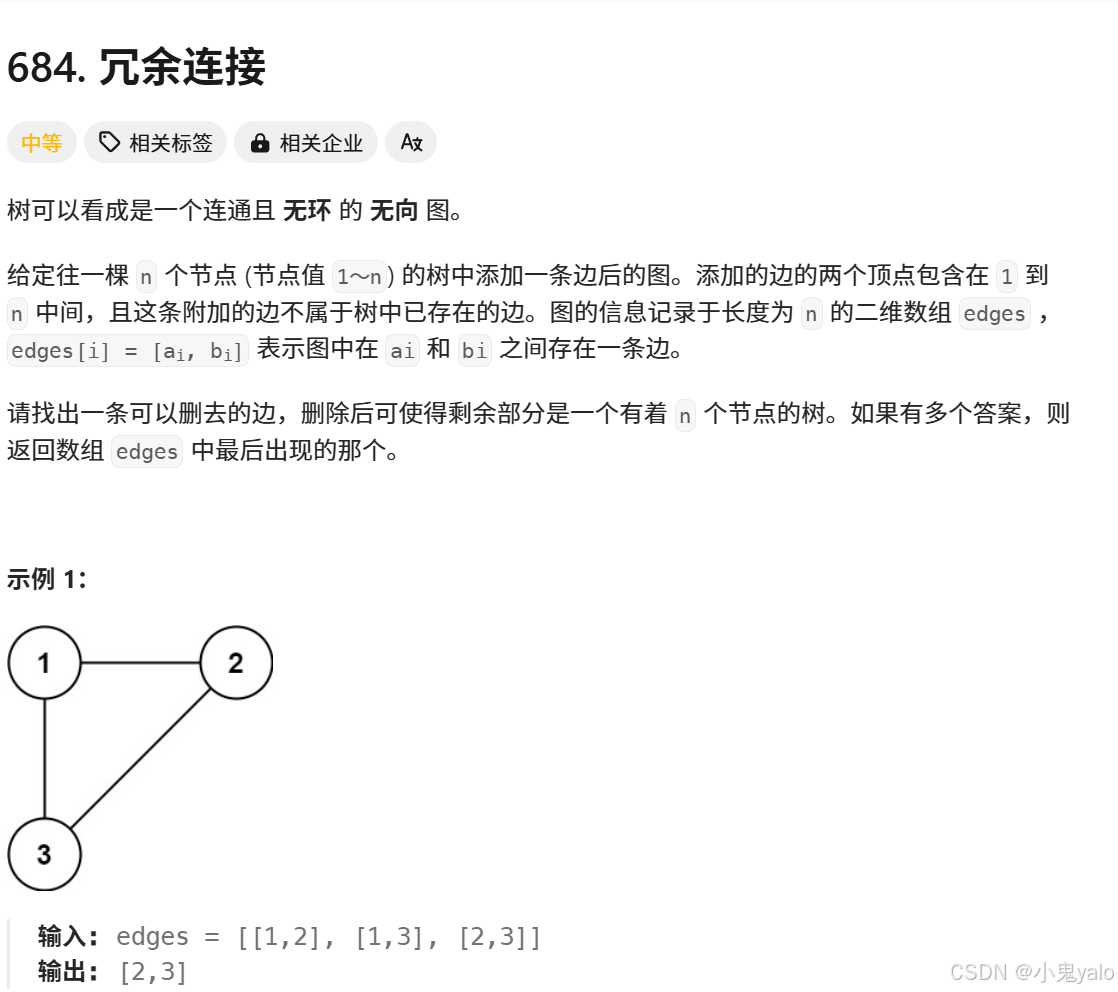
  1. class Solution {
  2. public:
  3.     vector<int> findRedundantConnection(vector<vector<int>>& edges) {
  4.         //遍历edges数组
  5.         //将在同一条边中的两个顶点放入一个集合
  6.         //如果这条边的两个顶点已经在同一个集合中，加入这条边后，会出现环 ，返回这条边
  7.         vector<int> ufs(1010);
  8.         int sz=edges.size();
  9.         //初始化时各元素自成一个集合，自己就是根
  10.         for(int i=0;i<sz;i++)
  11.         ufs[i]=i;
  12.         
  13.         for(int j=0;j<sz;j++)
  14.         {
  15.             //找到边的两个顶点所在的集合，也就是根节点
  16.             int root1=find(edges[j][0],ufs);
  17.             int root2=find(edges[j][1],ufs);
  18.             //如果在一个集合，加入这条边后，会出现环
  19.             if(root1==root2)
  20.             return edges[j];
  21.             else
  22.             {
  23.                 //两个集合独立，合并两个集合
  24.                 ufs[root1]=root2;
  25.             }
  26.         }
  27.         return {0,0};
  28.     }
  29.     int find(int num,vector<int>& ufs)
  30.     {
  31.         int root=num;
  32.         while(ufs[root]!=root)
  33.         root=ufs[root];
  34.         return root;
  35.     }
  36. };

等式方程的可满足性[OJ题]

本题链接：990. 等式方程的可满足性 - 力扣（LeetCode）

  1. class Solution {
  2. public:
  3.     bool equationsPossible(vector<string>& equations) {
  4.         //并查集
  5.         vector<int> ufs(26,-1);
  6.         auto findroot=[&](int x)
  7.         {
  8.             int parent=x;
  9.             while(ufs[parent]>=0)
  10.             parent=ufs[parent];
  11.             return parent;
  12.         };
  13.  
  14.         //将相等的放入同一集合中
  15.         for(auto& str:equations)
  16.             if(str[1]=='=')
  17.             {
  18.                 int root1=findroot(str[0]-'a');
  19.                 int root2=findroot(str[3]-'a');
  20.                  if(root1!=root2)
  21.                  {
  22.                     ufs[root1]+=ufs[root2];
  23.                     ufs[root2]=root1;
  24.                  }
  25.             }
  26.         //遇到！，如果在同一个集合，返回false
  27.         for(auto& str:equations)
  28.         {
  29.             if(str[1]=='!')
  30.             {
  31.                 int root1=findroot(str[0]-'a');
  32.                 int root2=findroot(str[3]-'a');
  33.                 if(root1==root2)
  34.                 return false;
  35.             }
  36.         }
  37.         return true;
  38.     }
  39. };

 

注：本文转载自blog.csdn.net的小鬼yalo的文章"https://blog.csdn.net/2401_82677021/article/details/145656330"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！