队列知识及编程练习总结

目录

一、背景知识 

二、队列的应用

（一）在Spring中的应用

（二）在其他框架中的应用

（三）在实际开发中的应用

三、相关编程练习

（一）用队列实现栈

（二）使用栈实现队列

（三）设计循环队列

（四）滑动窗口最大值 

（五）课程表

（六）队列的最大值

（七）用数组实现一个队列

干货分享，感谢您的阅读！祝你编程题必过！

一、背景知识 

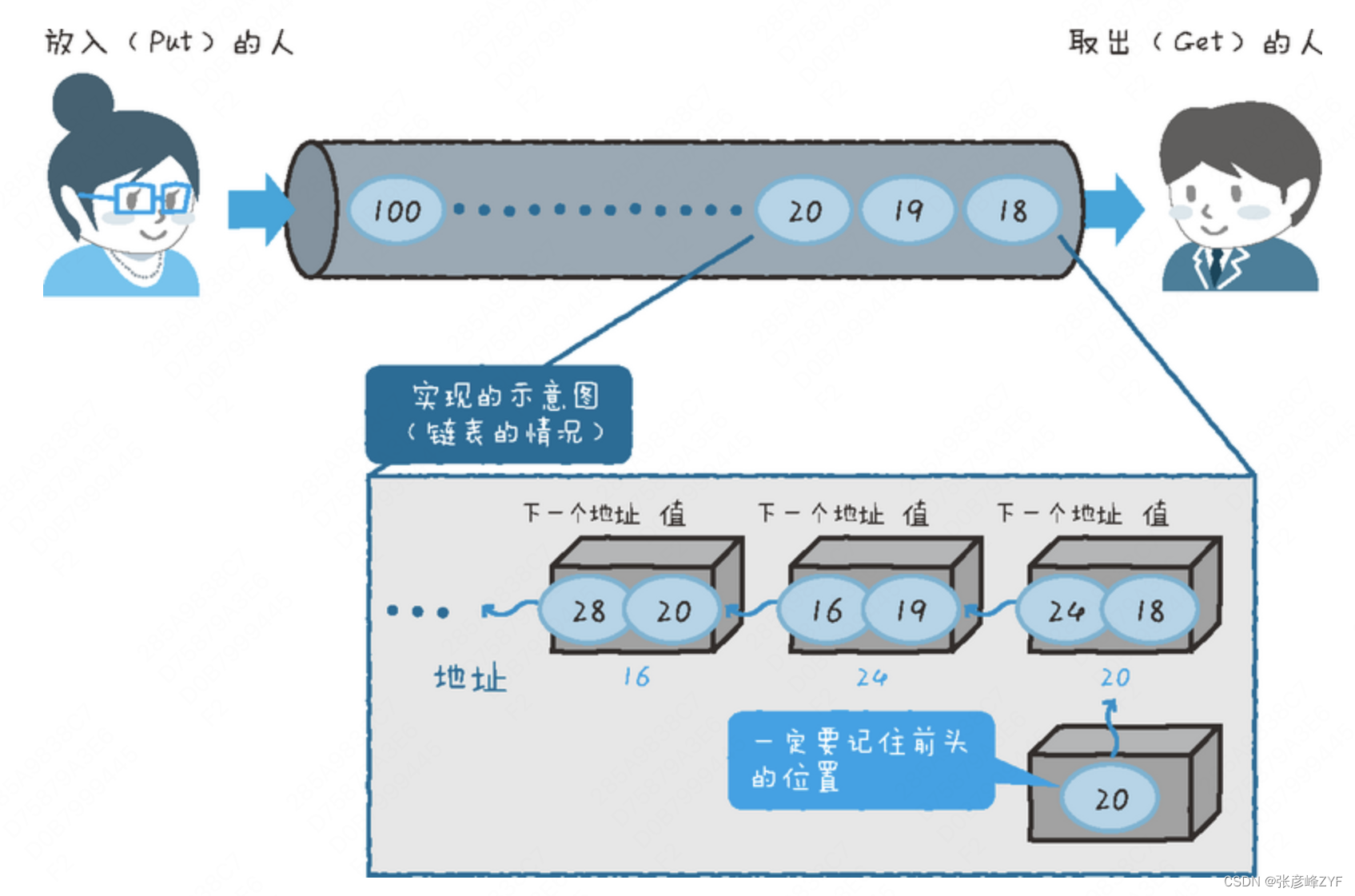
队列是一种常见的数据结构，其特点是先进先出（First-In-First-Out，FIFO），也就是最先入队的元素最先出队。队列可以用来实现任务调度、缓存、消息传递等应用场景。

队列通常有两个基本操作：入队（enqueue）和出队（dequeue）。入队操作将一个元素加入队列的尾部，出队操作将队列头部的元素移除并返回其值。队列还有一个获取队头元素但不移除的操作（peek）。

队列有多种实现方式，包括数组实现和链表实现。数组实现的队列通常需要指定一个固定的容量，而链表实现的队列可以动态增长。

队列还有一些变种，如双端队列（deque）和优先队列（priority queue）。双端队列支持在队头和队尾进行插入和删除操作，优先队列中元素按照一定的优先级顺序出队。

总的来说，队列的基本操作包括：

  1. 入队（enqueue）：将一个元素加入队列的尾部。
  2. 出队（dequeue）：将队列头部的元素移除并返回其值。
  3. 获取队头元素但不移除（peek）：返回队列头部的元素值，但不将其移除。
  4. 判断队列是否为空（isEmpty）：如果队列中没有元素则返回 true，否则返回 false。
  5. 判断队列是否已满（isFull）：如果队列已满则返回 true，否则返回 false。但是对于链表实现的队列来说，不需要判断队列是否已满，因为链表的长度是动态变化的。（对于数组实现的队列而言才有这个操作）

除了这些基本操作之外，队列的具体实现还可以包括其他的一些操作，例如扩容、缩容等。

按照以上的背景，展示举例：队列的大致流程就像是往管道中一个一个地放入小球，然后小球从管道前头一个个出来。（图来自图灵社区）

二、队列的应用

（一）在Spring中的应用

在 Spring 框架中，队列主要用于异步消息处理，其中的应用包括：

  1. Spring JMS（Java Message Service）：Spring JMS 可以使用 JMS 队列实现异步消息处理。消息生产者将消息发送到队列中，消息消费者从队列中获取消息并进行处理。
  2. Spring AMQP（Advanced Message Queuing Protocol）：Spring AMQP 是 Spring 对 AMQP 消息协议的支持，可以使用 AMQP 的队列实现异步消息处理。与 JMS 相比，AMQP 具有更强的消息路由和交换机管理能力。
  3. Spring Integration：Spring Integration 提供了丰富的消息通道和消息处理器，可以使用队列实现异步消息处理。
  4. Spring Batch：Spring Batch 是 Spring 提供的批处理框架，其中的 JobLauncher 实现了异步任务处理，使用了内部的任务队列进行任务调度。

总的来说，Spring 框架中队列的应用主要涉及异步消息处理，其背后的思想是将任务分发给多个线程或者处理器，提高任务的处理效率和并发能力。

（二）在其他框架中的应用

除了 Spring 框架，队列在其他一些框架中也有广泛的应用，例如：

  1. Apache Kafka：Apache Kafka 是一个分布式消息队列，被广泛用于大规模数据流处理和实时数据管道。它提供高可用、高可靠的消息传输服务，支持多个消费者和分区，同时还具有高性能和可扩展性。
  2. RabbitMQ：RabbitMQ 是一个 AMQP 实现，支持多种消息队列模式，包括点对点、发布/订阅和路由等。它具有高可用、高可靠性和高性能，支持多种客户端语言和多种平台。
  3. Redis：Redis 是一个内存中的数据结构存储系统，可以使用 Redis List 实现队列。它支持数据持久化、集群和复制，同时还支持多种数据结构操作和多种客户端语言。
  4. ActiveMQ：ActiveMQ 是一个开源的 JMS 实现，支持多种消息队列模式，包括点对点、发布/订阅和通配符等。它具有高可用、高可靠性和高性能，同时还支持多种客户端语言和多种平台。

总的来说，队列在分布式系统和大规模数据处理中扮演着重要的角色，被广泛应用于消息传输、任务调度、数据流处理等场景。

（三）在实际开发中的应用

在实际开发工作中，队列可以应用于多个场景，例如：

  1. 异步任务处理：当系统需要执行大量耗时的任务时，可以将任务放入队列中，由多个工作者线程异步地处理任务，从而提高系统的并发能力和性能。
  2. 消息队列：当系统需要在多个进程或者机器之间传递消息时，可以使用消息队列。生产者将消息放入队列中，消费者从队列中获取消息并进行处理，从而实现不同进程或者机器之间的异步通信。
  3. 数据流处理：当系统需要处理大规模的数据流时，可以使用队列将数据分配给多个处理节点进行处理。例如，将用户行为日志放入队列中，由多个处理节点进行数据分析和挖掘。
  4. 任务调度：当系统需要执行周期性的任务时，可以使用队列进行任务调度。将任务放入队列中，由任务调度器定时执行任务，并将执行结果返回给系统。
  5. 网络流量控制：当系统需要控制网络流量时，可以使用队列进行流量控制。例如，将网络请求放入队列中，限制同时处理请求的数量，从而避免系统崩溃。

总的来说，队列在实际开发工作中应用广泛，涉及任务调度、消息传输、数据处理等多个场景，可以提高系统的并发能力和性能，提高系统的可靠性和稳定性。

三、相关编程练习

（一）用队列实现栈

与栈知识及编程练习总结_张彦峰ZYF的博客-CSDN博客中练习三（五）相同，请直接跳转阅读。

（二）使用栈实现队列

与栈知识及编程练习总结_张彦峰ZYF的博客-CSDN博客中练习三（四）相同，请直接跳转阅读。

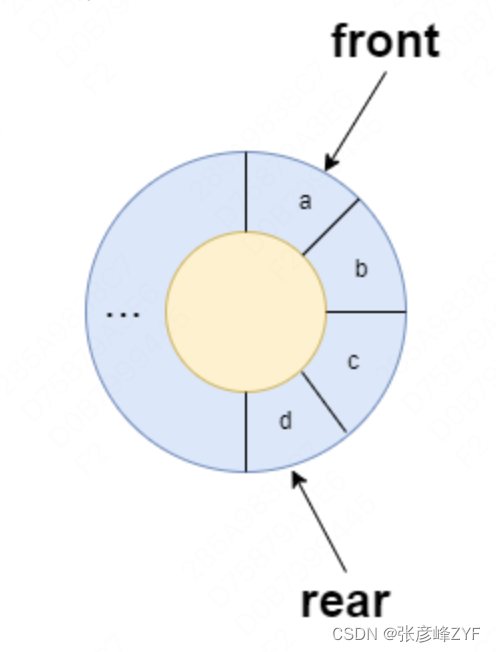
（三）设计循环队列

题目描述：设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

  • MyCircularQueue(k): 构造器，设置队列长度为 k 。
  • Front: 从队首获取元素。如果队列为空，返回 -1 。
  • Rear: 获取队尾元素。如果队列为空，返回 -1 。
  • enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
  • deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
  • isEmpty(): 检查循环队列是否为空。
  • isFull(): 检查循环队列是否已满。

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4
 

提示：

  • 所有的值都在 0 至 1000 的范围内；
  • 操作数将在 1 至 1000 的范围内；
  • 请不要使用内置的队列库。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/design-circular-queue

解题思路

比较常见的实现方式，使用一个数组和两个指针 front 和 rear 分别指向队列的头部和尾部，同时使用一个变量 size 维护队列中元素的个数，在 enQueue() 和 deQueue() 方法中，需要将指针向后移动一位，并使用取模操作保证指针不会越界。在 enQueue() 方法中，还需要注意特殊情况，即当队列为空时，需要将 front 指向插入的元素。

这个实现方式的时间复杂度为O(1)。

 具体代码展示

  1. package org.zyf.javabasic.letcode.queue;
  2.  
  3. /**
  4.  * @author yanfengzhang
  5.  * @description 设计你的循环队列实现。
  6.  * 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
  7.  * 
  8.  * 循环队列的一个好处是我们可以利用这个队列之前用过的空间。
  9.  * 在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。
  10.  * 但是使用循环队列，我们能使用这些空间去存储新的值。
  11.  * @date 2023/4/9  14:58
  12.  */
  13. public class MyCircularQueue {
  14.     /*存储队列元素的数组*/
  15.     private int[] data;
  16.     /*队头指针，指向队头元素*/
  17.     private int front;
  18.     /*队尾指针，指向队尾元素的下一个位置*/
  19.     private int rear;
  20.     /*队列中元素的个数*/
  21.     private int size;
  22.  
  23.     public MyCircularQueue(int k) {
  24.         /*初始化数组*/
  25.         data = new int[k];
  26.         /*初始时队头指针指向 -1*/
  27.         front = -1;
  28.         /*初始时队尾指针指向 -1*/
  29.         rear = -1;
  30.         /*初始时队列中元素个数为 0*/
  31.         size = 0;
  32.     }
  33.  
  34.     public boolean enQueue(int value) {
  35.         /*队列已满，插入失败*/
  36.         if (isFull()) {
  37.             return false;
  38.         }
  39.         /*队列为空，需要将 front 指向插入的元素*/
  40.         if (isEmpty()) {
  41.             front = 0;
  42.         }
  43.         /*队尾指针向后移动一位，并使用取模操作保证指针不会越界*/
  44.         rear = (rear + 1) % data.length;
  45.         /*在队尾插入元素*/
  46.         data[rear] = value;
  47.         /*队列中元素个数加一*/
  48.         size++;
  49.         /*插入成功*/
  50.         return true;
  51.     }
  52.  
  53.     public boolean deQueue() {
  54.         /*队列为空，删除失败*/
  55.         if (isEmpty()) {
  56.             return false;
  57.         }
  58.         /*队列中只有一个元素，需要将 front 和 rear 指向 -1*/
  59.         if (front == rear) {
  60.             front = -1;
  61.             rear = -1;
  62.         }
  63.         /*队列中有多个元素，需要将 front 指针向后移动一位*/
  64.         else {
  65.             /*队头指针向后移动一位，并使用取模操作保证指针不会越界*/
  66.             front = (front + 1) % data.length;
  67.         }
  68.         /*队列中元素个数减一*/
  69.         size--;
  70.         /*删除成功*/
  71.         return true;
  72.     }
  73.  
  74.     public int Front() {
  75.         if (isEmpty()) {
  76.             /*队列为空，返回 -1*/
  77.             return -1;
  78.         }
  79.         /*返回队头元素*/
  80.         return data[front];
  81.     }
  82.  
  83.     public int Rear() {
  84.         /*队列为空，返回 -1*/
  85.         if (isEmpty()) {
  86.             return -1;
  87.         }
  88.         /*返回队尾元素*/
  89.         return data[rear];
  90.     }
  91.  
  92.     public boolean isEmpty() {
  93.         /*判断队列是否为空*/
  94.         return size == 0;
  95.     }
  96.  
  97.     public boolean isFull() {
  98.         /*判断队列是否已满*/
  99.         return size == data.length;
  100.     }
  101.  
  102.     /**
  103.      * 在该测试代码中，我们创建了一个容量为 3 的循环队列，
  104.      * 然后进行了一系列操作来测试该类的实现是否正确。
  105.      * 最后输出的结果符合预期，说明该循环队列的实现是正确的。
  106.      */
  107.     public static void main(String[] args) {
  108.         /*创建容量为 3 的循环队列*/
  109.         MyCircularQueue circularQueue = new MyCircularQueue(3);
  110.         /*输出 true，队列变为 [1]*/
  111.         System.out.println(circularQueue.enQueue(1));
  112.         /*输出 true，队列变为 [1, 2]*/
  113.         System.out.println(circularQueue.enQueue(2));
  114.         /*输出 true，队列变为 [1, 2, 3]*/
  115.         System.out.println(circularQueue.enQueue(3));
  116.         /*输出 false，队列已满，插入失败*/
  117.         System.out.println(circularQueue.enQueue(4));
  118.         /*输出 3，队尾元素为 3*/
  119.         System.out.println(circularQueue.Rear());
  120.         /*输出 true，队列已满*/
  121.         System.out.println(circularQueue.isFull());
  122.         /*输出 true，队列变为 [2, 3]*/
  123.         System.out.println(circularQueue.deQueue());
  124.         /*输出 true，队列变为 [2, 3, 4]*/
  125.         System.out.println(circularQueue.enQueue(4));
  126.         /*输出 4，队尾元素为 4*/
  127.         System.out.println(circularQueue.Rear());
  128.     }
  129. }

（四）滑动窗口最大值 

题目描述：给定一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例:输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3       输出: [3,3,5,5,6,7]

解释:滑动窗口的位置 最大值

  • [1 3 -1] -3 5 3 6 7 3
  • 1 [3 -1 -3] 5 3 6 7 3
  • 1 3 [-1 -3 5] 3 6 7 5
  • 1 3 -1 [-3 5 3] 6 7 5
  • 1 3 -1 -3 [5 3 6] 7 6
  • 1 3 -1 -3 5 [3 6 7] 7

提示：你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。

进阶：你能在线性时间复杂度内解决此题吗？

解题思路

滑动窗口最大值问题可以使用单调队列来解决，具体思路如下：

  1. 我们使用双端队列 deque，存储数组的下标。deque 中的元素按照从大到小的顺序排列，即 deque 中的第一个元素是滑动窗口中的最大值。
  2. 我们遍历数组，依次将元素放入 deque 中。当元素个数大于 k 时，我们需要将 deque 的第一个元素弹出，因为它不在滑动窗口中了。
  3. 对于新加入 deque 的元素，从队尾开始比较，如果队尾的元素比当前元素小，则说明队尾的元素不可能是滑动窗口中的最大值，将其弹出。直到队尾的元素比当前元素大，或者 deque 为空，我们再将当前元素插入队尾。
  4. 每次队列中的最大值即为 deque 的第一个元素，我们将其存入结果数组中。

由于每个元素最多进 deque 和出 deque 一次，因此时间复杂度为 O(n)。

需要注意的是，deque 中存储的是数组中元素的下标，而不是元素本身。因此在计算 deque 中的最大值时，需要根据下标从原数组中取出对应的元素。

具体代码展示

  1. package org.zyf.javabasic.letcode.queue;
  2.  
  3. import java.util.Arrays;
  4. import java.util.Deque;
  5. import java.util.LinkedList;
  6.  
  7. /**
  8.  * @author yanfengzhang
  9.  * @description 给定一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。
  10.  * 你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
  11.  * 返回滑动窗口中的最大值。
  12.  * @date 2023/4/9  15:23
  13.  */
  14. public class MaxSlidingWindow {
  15.  
  16.     /**
  17.      * 1 我们使用双端队列 deque，存储数组的下标。deque 中的元素按照从大到小的顺序排列，即 deque 中的第一个元素是滑动窗口中的最大值。
  18.      * 2 我们遍历数组，依次将元素放入 deque 中。当元素个数大于 k 时，我们需要将 deque 的第一个元素弹出，因为它不在滑动窗口中了。
  19.      * 3 对于新加入 deque 的元素，从队尾开始比较，如果队尾的元素比当前元素小，
  20.      * 则说明队尾的元素不可能是滑动窗口中的最大值，将其弹出。
  21.      * 直到队尾的元素比当前元素大，或者 deque 为空，我们再将当前元素插入队尾。
  22.      * 4 每次队列中的最大值即为 deque 的第一个元素，我们将其存入结果数组中。
  23.      */
  24.     public int[] maxSlidingWindow(int[] nums, int k) {
  25.         int n = nums.length;
  26.         if (n == 0) {
  27.             return new int[0];
  28.         }
  29.         if (k == 1) {
  30.             return nums;
  31.         }
  32.  
  33.         /*双端队列，存储数组下标*/
  34.         Deque deque = new LinkedList<>();
  35.  
  36.         /*初始化队列，从 0 到 k - 1，把队列中比 nums[i] 小的元素全部弹出*/
  37.         for (int i = 0; i < k; i++) {
  38.             while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
  39.                 deque.pollLast();
  40.             }
  41.             deque.offerLast(i);
  42.         }
  43.  
  44.         int[] ans = new int[n - k + 1];
  45.         ans[0] = nums[deque.peekFirst()];
  46.  
  47.         /*遍历数组，维护队列中的元素*/
  48.         for (int i = k; i < n; i++) {
  49.             /*判断队首是否在滑动窗口中*/
  50.             if (deque.peekFirst() <= i - k) {
  51.                 deque.pollFirst();
  52.             }
  53.  
  54.             /*把队列中比 nums[i] 小的元素全部弹出*/
  55.             while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
  56.                 deque.pollLast();
  57.             }
  58.  
  59.             /*将当前元素插入队尾*/
  60.             deque.offerLast(i);
  61.  
  62.             ans[i - k + 1] = nums[deque.peekFirst()];
  63.         }
  64.  
  65.         return ans;
  66.     }
  67.  
  68.     public static void main(String[] args) {
  69.         int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
  70.         int k = 3;
  71.         int[] result = new MaxSlidingWindow().maxSlidingWindow(nums, k);
  72.         /*输出：[3, 3, 5, 5, 6, 7]*/
  73.         System.out.println(Arrays.toString(result));
  74.  
  75.     }
  76. }

（五）课程表

题目描述：你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

 提示：

  • 1 <= numCourses <= 105
  • 0 <= prerequisites.length <= 5000
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • prerequisites[i] 中的所有课程对 互不相同

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/course-schedule

解题思路

该问题可以抽象成一个有向图，课程之间的先修关系可以表示为图中的边。因此，该问题就转化为在有向图中判断是否存在环。若存在环，那么就无法完成所有课程的学习，否则就可以完成。

使用拓扑排序算法可以解决该问题。拓扑排序可以输出图的节点，满足节点的前驱节点已经全部输出。对于本题，我们可以使用拓扑排序来判断有向图中是否存在环。具体做法是，每次选择一个入度为 0 的节点，并移除该节点以及以该节点为起点的所有边，重复这个过程直到图为空，若过程中存在没有入度为 0 的节点的情况，那么就说明图中存在环。如果最终能够将所有节点输出，那么就说明没有环，可以完成所有课程的学习。

也可以使用队列实现拓扑排序算法。具体实现方法是：

  1. 统计所有节点的入度，将入度为 0 的节点加入队列。
  2. 取出队首节点，输出该节点，并将以该节点为起点的所有边移除，更新它们的入度。如果某个节点入度变为 0，则将该节点加入队列。
  3. 重复第 2 步，直到队列为空或者无法再取出入度为 0 的节点。

如果最终能够输出所有节点，说明不存在环；否则，说明存在环。

具体代码展示

  1. package org.zyf.javabasic.letcode.queue;
  2.  
  3. import java.util.LinkedList;
  4. import java.util.Queue;
  5.  
  6. /**
  7.  * @author yanfengzhang
  8.  * @description 你这个学期必须选修 numCourses 门课程，记为0到numCourses - 1 。
  9.  * 在选修某些课程之前需要一些先修课程。
  10.  * 先修课程按数组prerequisites 给出，其中prerequisites[i] = [ai, bi] ，表示如果要学习课程ai 则 必须 先学习课程bi 。
  11.  * 
  12.  * 例如，先修课程对[0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
  13.  * 请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。
  14.  * @date 2023/4/9  15:55
  15.  */
  16. public class CanFinishCourses {
  17.  
  18.     /**
  19.      * 使用队列实现拓扑排序算法。具体实现方法是：
  20.      * 统计所有节点的入度，将入度为 0 的节点加入队列。
  21.      * 取出队首节点，输出该节点，并将以该节点为起点的所有边移除，更新它们的入度。如果某个节点入度变为 0，则将该节点加入队列。
  22.      * 重复第 2 步，直到队列为空或者无法再取出入度为 0 的节点。
  23.      * 如果最终能够输出所有节点，说明不存在环；否则，说明存在环。
  24.      */
  25.     public boolean canFinish(int numCourses, int[][] prerequisites) {
  26.         /*记录每个节点的入度*/
  27.         int[] inDegree = new int[numCourses];
  28.         for (int[] pre : prerequisites) {
  29.             inDegree[pre[0]]++;
  30.         }
  31.  
  32.         Queue queue = new LinkedList<>();
  33.         /*将入度为 0 的节点加入队列*/
  34.         for (int i = 0; i < numCourses; i++) {
  35.             if (inDegree[i] == 0) {
  36.                 queue.offer(i);
  37.             }
  38.         }
  39.  
  40.         int count = 0;
  41.         /*取出队首节点，输出该节点，并将以该节点为起点的所有边移除，更新它们的入度*/
  42.         while (!queue.isEmpty()) {
  43.             int curr = queue.poll();
  44.             count++;
  45.             for (int[] pre : prerequisites) {
  46.                 if (pre[1] == curr) {
  47.                     inDegree[pre[0]]--;
  48.                     if (inDegree[pre[0]] == 0) {
  49.                         queue.offer(pre[0]);
  50.                     }
  51.                 }
  52.             }
  53.         }
  54.  
  55.         /*如果最终能够输出所有节点，说明不存在环；否则，说明存在环*/
  56.         return count == numCourses;
  57.     }
  58. }

（六）队列的最大值

题目描述：请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

 限制：

  • 1 <= push_back,pop_front,max_value的总操作数 <= 10000
  • 1 <= value <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/dui-lie-de-zui-da-zhi-lcof

解题思路

可以使用两个队列来实现，一个队列用来存储插入的元素，另一个队列用来存储当前队列中的最大值。

具体实现时，我们可以使用两个 LinkedList 来实现双端队列，一个队列用来存储插入的元素，另一个队列用来存储当前队列中的最大值。

每次插入元素时，先将该元素插入到存储元素的队列中，然后将最大值队列中小于等于该元素的元素全部弹出，保证最大值队列中的元素始终是递减的。然后将该元素插入到最大值队列中。

当需要弹出队首元素时，如果队首元素等于最大值队列中的第一个元素，则同时弹出该元素。

由于每个元素最多只会被弹入和弹出一次，因此总时间复杂度为O(n)，均摊时间复杂度为 O(1)。

具体代码展示

  1. package org.zyf.javabasic.letcode.queue;
  2.  
  3. import java.util.LinkedList;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 请定义一个队列并实现函数 max_value 得到队列里的最大值，
  8.  * 要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
  9.  * 
  10.  * 若队列为空，pop_front 和 max_value需要返回 -1
  11.  * @date 2023/4/9  16:19
  12.  */
  13. public class MaxQueue {
  14.     /*存储正常数据的队列*/
  15.     private LinkedList queue;
  16.     /*存储当前队列中最大值的队列*/
  17.     private LinkedList maxQueue;
  18.  
  19.     public MaxQueue() {
  20.         queue = new LinkedList<>();
  21.         maxQueue = new LinkedList<>();
  22.     }
  23.  
  24.     public int max_value() {
  25.         if (maxQueue.isEmpty()) {
  26.             return -1;
  27.         }
  28.         /*返回最大值队列的队首元素*/
  29.         return maxQueue.peekFirst();
  30.     }
  31.  
  32.     public void push_back(int value) {
  33.         /*将元素加入正常队列*/
  34.         queue.offerLast(value);
  35.         while (!maxQueue.isEmpty() && maxQueue.peekLast() < value) {
  36.             /*将小于当前元素的元素从最大值队列中弹出*/
  37.             maxQueue.pollLast();
  38.         }
  39.         /*将当前元素加入最大值队列*/
  40.         maxQueue.offerLast(value);
  41.     }
  42.  
  43.     public int pop_front() {
  44.         if (queue.isEmpty()) {
  45.             return -1;
  46.         }
  47.         /*弹出正常队列的队首元素*/
  48.         int front = queue.pollFirst();
  49.         if (front == maxQueue.peekFirst()) {
  50.             /*如果该元素是最大值队列的队首元素，则同时弹出*/
  51.             maxQueue.pollFirst();
  52.         }
  53.         return front;
  54.     }
  55.  
  56.     public static void main(String[] args) {
  57.         MaxQueue q = new MaxQueue();
  58.         /*输出 -1*/
  59.         System.out.println(q.max_value());
  60.         q.push_back(1);
  61.         q.push_back(3);
  62.         q.push_back(2);
  63.         /*输出 3*/
  64.         System.out.println(q.max_value());
  65.         /*输出 1*/
  66.         System.out.println(q.pop_front());
  67.         /*输出 3*/
  68.         System.out.println(q.max_value());
  69.         /*输出 3*/
  70.         System.out.println(q.pop_front());
  71.         /*输出 2*/
  72.         System.out.println(q.max_value());
  73.         /*输出 2*/
  74.         System.out.println(q.pop_front());
  75.         /*输出 -1*/
  76.         System.out.println(q.max_value());
  77.     }
  78.  
  79. }

（七）用数组实现一个队列

题目描述：设计并实现一个基于数组的队列（Queue）数据结构，要求支持入队（enqueue）和出队（dequeue）操作，并能够正确地维护队列的顺序。

解题思路

要使用数组实现一个队列，可以利用数组的特性进行操作。以下是一种常见的实现思路：

  1. 创建一个固定大小的数组，用于存储队列的元素。
  2. 使用两个指针，分别指向队列的头部和尾部。
  3. 初始时，头部和尾部指针都指向数组的起始位置。
  4. 入队操作：将元素添加到尾部指针所指向的位置，然后将尾部指针后移一位。
  5. 出队操作：将头部指针所指向的元素移除，并将头部指针后移一位。
  6. 队列为空时，头部和尾部指针指向同一个位置。

具体代码展示

  1. package org.zyf.javabasic.letcode.queue;
  2.  
  3. /**
  4.  * @author yanfengzhang
  5.  * @description 设计并实现一个基于数组的队列（Queue）数据结构，
  6.  * 要求支持入队（enqueue）和出队（dequeue）操作，
  7.  * 并能够正确地维护队列的顺序。
  8.  * enqueue 和 dequeue 操作的时间复杂度为 O(1)，isEmpty 和 size 方法的时间复杂度也为 O(1)。
  9.  *
  10.  * 要使用数组实现一个队列，可以利用数组的特性进行操作。以下是一种常见的实现思路：
  11.  * 	1.	创建一个固定大小的数组，用于存储队列的元素。
  12.  * 	2.	使用两个指针，分别指向队列的头部和尾部。
  13.  * 	3.	初始时，头部和尾部指针都指向数组的起始位置。
  14.  * 	4.	入队操作：将元素添加到尾部指针所指向的位置，然后将尾部指针后移一位。
  15.  * 	5.	出队操作：将头部指针所指向的元素移除，并将头部指针后移一位。
  16.  * 	6.	队列为空时，头部和尾部指针指向同一个位置。
  17.  * @date 2023/6/14  23:51
  18.  */
  19. public class ImplementQueueUseArray {
  20.     private int capacity;
  21.     private int[] queue;
  22.     // 头部指针
  23.     private int head;
  24.     // 尾部指针
  25.     private int tail;
  26.  
  27.     public ImplementQueueUseArray(int capacity) {
  28.         this.capacity = capacity;
  29.         this.queue = new int[capacity];
  30.         this.head = 0;
  31.         this.tail = 0;
  32.     }
  33.  
  34.     public void enqueue(int item) {
  35.         if (tail == capacity) {
  36.             // 队列已满
  37.             throw new IndexOutOfBoundsException("Queue is full");
  38.         }
  39.         queue[tail] = item;
  40.         tail++;
  41.     }
  42.  
  43.     public int dequeue() {
  44.         if (head == tail) {
  45.             // 队列为空
  46.             throw new IndexOutOfBoundsException("Queue is empty");
  47.         }
  48.         int item = queue[head];
  49.         head++;
  50.         return item;
  51.     }
  52.  
  53.     public boolean isEmpty() {
  54.         return head == tail;
  55.     }
  56.  
  57.     public int size() {
  58.         return tail - head;
  59.     }
  60.  
  61.     public static void main(String[] args) {
  62.         ImplementQueueUseArray queue = new ImplementQueueUseArray(5);
  63.  
  64.         queue.enqueue(10);
  65.         queue.enqueue(20);
  66.         queue.enqueue(30);
  67.  
  68.         System.out.println("Size of queue: " + queue.size());
  69.  
  70.         int item1 = queue.dequeue();
  71.         int item2 = queue.dequeue();
  72.  
  73.         System.out.println("Dequeued items: " + item1 + ", " + item2);
  74.         System.out.println("Size of queue after dequeue: " + queue.size());
  75.     }
  76. }

文章知识点与官方知识档案匹配，可进一步学习相关知识
算法技能树首页概览62532 人正在系统学习中
注：本文转载自blog.csdn.net的张彦峰ZYF的文章"https://blog.csdn.net/xiaofeng10330111/article/details/130037195"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！