栈知识及编程练习总结

目录

一、背景知识

二、栈的应用

（一）在Spring或计算机科学中的应用举例

（二）实际开发中的应用举例

三、相关编程练习

（一）有效的括号（Valid Parentheses）

（二）最小栈（Min Stack）

（三）每日温度（Daily Temperatures）

（四）用栈实现队列（Implement Queue using Stacks）

（五）用队列实现栈（Implement Stack using Queues）

（六）接雨水（Trapping Rain Water）

（七）逆波兰表达式求值（Evaluate Reverse Polish Notation）

（八）基本计算器（Basic Calculator）

（九）简化路径（Simplify Path）

  (十) 岛屿数量

扩展：其他最优解法展示

（十一）用数组实现一个栈

（十二）基本数学运算表达式求值

（十三） IP 范围判断

干货分享，感谢您的阅读！祝你逢考必过！

一、背景知识

栈（Stack）是一种线性数据结构，它遵循后进先出（Last-In-First-Out，LIFO）的原则，这意味着最近添加的元素最先被访问，而最先添加的元素最后被访问。这种特性使栈非常适合用于某些应用，比如函数调用、表达式求值、括号匹配、回溯等。

当我们需要保存一些数据，而且需要以特定的顺序进行访问时，栈就是一个非常有用的数据结构。它通常有以下三种基本操作：

  1. 入栈（Push）：向栈中添加元素。元素会被添加到栈顶，也就是最后一个元素之后。
  2. 出栈（Pop）：从栈中移除并返回栈顶元素。栈顶元素是最后一个入栈的元素。
  3. 查看栈顶元素（Peek）：查看栈顶元素，但是不从栈中移除它。

另外，还有两个与栈相关的概念：栈底和栈顶。栈底是栈的第一个元素，而栈顶是最后一个元素。因为栈是后进先出的，所以最后进入栈的元素是在栈顶，而最先进入栈的元素是在栈底。

栈还有一些重要的特点，如下所示：

  1. 空栈：如果栈中没有任何元素，则称之为空栈。
  2. 栈的大小：栈的大小表示栈中可以存储多少元素。当栈的大小已满时，再次尝试将元素入栈会导致栈溢出。
  3. 动态栈：动态栈是一种特殊类型的栈，可以根据需要自动增加或减少大小。这种栈的大小不是固定的，而是根据需要动态变化的。

按照以上的背景，展示举例：在写程序的时候，会碰到函数 A 要调用函数 B，函数 B 要调用函数 C 这样连续的处理。这个时候，在函数 A 的上面是函数 B，函数 B 的上面是函数 C。（图来自图灵社区）

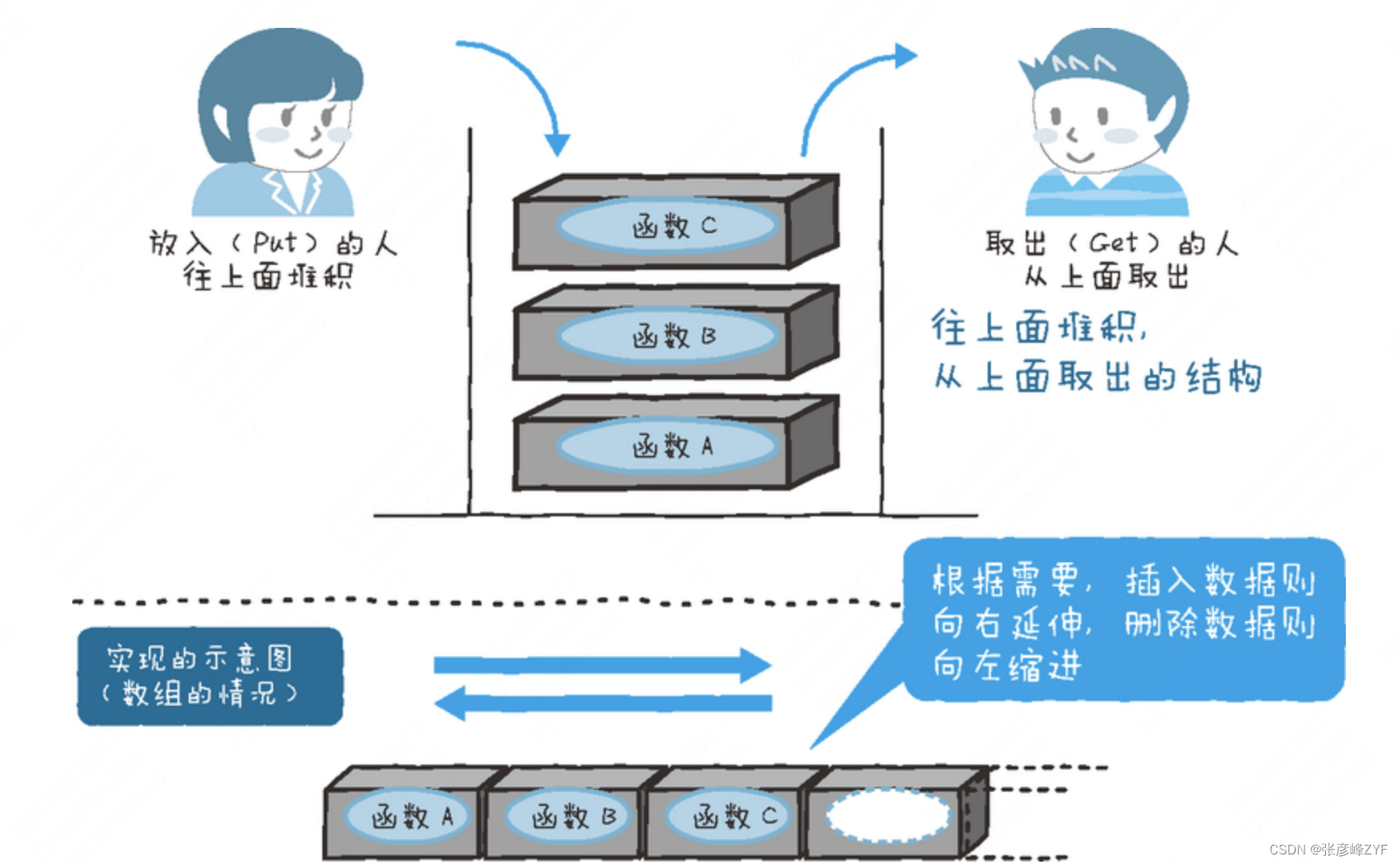
二、栈的应用

（一）在Spring或计算机科学中的应用举例

在 Spring 底层中，栈数据结构经常用于实现方法调用栈。Spring 框架的核心是 IoC 容器和 AOP 框架，而这些框架的实现都需要大量的方法调用。当我们使用 Spring 调用一个方法时，Spring 会将该方法及其参数压入一个方法调用栈中，然后执行该方法。如果该方法又调用了其他方法，则 Spring 会将这些方法和它们的参数也压入方法调用栈中，直到所有方法执行完毕并返回结果。

此外，在 Web 应用程序中，栈数据结构也经常用于处理 HTTP 请求。当一个请求到达服务器时，Web 服务器会将该请求添加到请求队列中，然后使用栈数据结构来处理请求。每个请求都可以看作是一个方法调用，因此服务器可以使用栈来实现方法调用栈，以便管理请求处理流程。

当然，栈数据结构在计算机科学中有许多其他应用，以下是一些例子：

  1. 编译器和解释器中，栈常用于存储编译或解释器上下文，以便实现程序的递归或迭代执行。
  2. 操作系统中，栈被用于存储程序调用栈、系统调用和中断处理。
  3. 数据库管理系统中，栈被用于实现查询操作的解析和执行。
  4. 网络路由器中，栈被用于存储路由表，以便实现路由选择算法。
  5. 图形学中，栈被用于存储矩阵堆栈，以便实现变换操作。
  6. 数学中，栈被用于实现逆波兰表达式和表达式求值等算法。
  7. 计算机图形学中，栈被用于实现渲染管道，以便对图像进行各种变换和处理。

总之，栈数据结构是计算机科学中非常常见和有用的数据结构，被广泛应用于许多领域，包括编程语言、操作系统、数据库管理系统、网络通信、图形学和数学等。

（二）实际开发中的应用举例

在实际开发中，栈数据结构的应用也非常广泛。以下是一些实际开发中常见的栈应用举例：

  1. 浏览器的前进和后退功能。在浏览器中，用户可以通过点击“后退”和“前进”按钮来浏览他们之前访问过的网页。这些网页的访问历史被存储在栈中，每当用户点击“后退”或“前进”按钮时，浏览器就会从栈中弹出（或推入）一个网页。
  2. 程序调用堆栈。在计算机程序中，方法调用通常被实现为栈结构。每当一个方法被调用时，它的参数和返回地址会被压入栈中，然后在该方法执行完毕后被弹出。
  3. 表达式求值。在编写编译器或计算器程序时，常常需要实现表达式求值算法。这些算法通常使用栈来实现中间计算结果的存储和操作。
  4. 括号匹配。在编写程序时，常常需要对括号进行匹配和检查。这个问题可以通过使用栈来解决，将左括号压入栈中，遇到右括号时弹出栈顶元素并检查是否匹配。
  5. 逆波兰表达式求值。逆波兰表达式是一种无括号的数学表达式，使用栈可以方便地对逆波兰表达式进行求值。
  6. 回文字符串检查。回文字符串是一种正反读都相同的字符串，例如“level”和“racecar”。这个问题可以通过使用栈来解决，将字符串的一半字符压入栈中，然后从栈中弹出元素并与剩余字符进行比较。
  7. 缓存回退。在一些应用程序中，用户可能需要在多个页面之间切换。为了提高性能，程序通常会使用栈来缓存用户的页面历史，以便快速回退到之前的页面。

三、相关编程练习

（一）有效的括号（Valid Parentheses）

题目描述：给定一个只包括括号的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。

示例 1：输入：s = "()"            输出：true

示例 2：输入：s = "()[]{}"       输出：true

示例 3：输入：s = "(]"            输出：false

示例 4：输入：s = "([)]"          输出：false

示例 5：输入：s = "{[]}"          输出：true

提示：

  1. 1 <= s.length <= 104
  2. s 仅由括号 '()[]{}' 组成

解题思路

这道题的最优解是使用栈来解决。

我们可以遍历给定字符串，对于每个左括号，将其对应的右括号压入栈中，当遇到右括号时，弹出栈顶元素并判断是否与该右括号相同，若相同则继续遍历，若不相同则该字符串不合法。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 给定一个只包括括号的字符串 s ，判断字符串是否有效。
  8.  * 有效字符串需满足：左括号必须用相同类型的右括号闭合。
  9.  * 左括号必须以正确的顺序闭合。
  10.  * 示例 1：输入：s = "()"            输出：true
  11.  * 示例 2：输入：s = "()[]{}"        输出：true
  12.  * 示例 3：输入：s = "(]"            输出：false
  13.  * 示例 4：输入：s = "([)]"          输出：false
  14.  * 示例 5：输入：s = "{[]}"          输出：true
  15.  * 
  16.  * 提示：
  17.  * 1 <= s.length <= 104
  18.  * s 仅由括号 '()[]{}' 组成
  19.  * @date 2023/4/8  22:17
  20.  */
  21. public class ValidStr {
  22.  
  23.     /**
  24.      * 最优解是使用栈来解决。
  25.      * 
  26.      * 我们可以遍历给定字符串，
  27.      * 对于每个左括号，将其对应的右括号压入栈中，
  28.      * 当遇到右括号时，弹出栈顶元素并判断是否与该右括号相同，
  29.      * 若相同则继续遍历，若不相同则该字符串不合法。
  30.      */
  31.     public boolean isValid(String s) {
  32.         Stack stack = new Stack<>();
  33.         for (int i = 0; i < s.length(); i++) {
  34.             char c = s.charAt(i);
  35.             if (c == '(' || c == '[' || c == '{') {
  36.                 stack.push(c);
  37.             } else {
  38.                 if (stack.isEmpty()) {
  39.                     return false;
  40.                 }
  41.                 char top = stack.peek();
  42.                 if ((top == '(' && c == ')') 
  43.                         || (top == '[' && c == ']') 
  44.                         || (top == '{' && c == '}')) {
  45.                     stack.pop();
  46.                 } else {
  47.                     return false;
  48.                 }
  49.             }
  50.         }
  51.         return stack.isEmpty();
  52.     }
  53.  
  54.     public static void main(String[] args) {
  55.         /*验证有效的括号代码*/
  56.         String s = "()[]{}";
  57.         boolean result = new ValidStr().isValid(s);
  58.         System.out.println(result);
  59.  
  60.         s = "(]";
  61.         result = new ValidStr().isValid(s);
  62.         System.out.println(result);
  63.  
  64.         s = "([)]";
  65.         result = new ValidStr().isValid(s);
  66.         System.out.println(result);
  67.  
  68.         s = "{[]}";
  69.         result = new ValidStr().isValid(s);
  70.         System.out.println(result);
  71.     }
  72. }

（二）最小栈（Min Stack）

题目描述：设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

  • push(x) —— 将元素 x 推入栈中。
  • pop() —— 删除栈顶的元素。
  • top() —— 获取栈顶元素。
  • getMin() —— 检索栈中的最小元素。

示例:

输入：["MinStack","push","push","push","getMin","pop","top","getMin"]

[[],[-2],[0],[-3],[],[],[],[]]

输出：[null,null,null,null,-3,null,0,-2]

解释：

MinStack minStack = new MinStack();

minStack.push(-2);

minStack.push(0);

minStack.push(-3);

minStack.getMin(); // 返回 -3

minStack.pop();

minStack.top(); // 返回 0

minStack.getMin(); // 返回 -2

提示：

  • pop、top 和 getMin 操作总是在 非空栈 上调用。

解题思路

该问题的最优解是使用一个栈和一个辅助栈来实现。

在栈中存储元素，辅助栈中存储当前栈中的最小值。

每次压入元素时，将其压入栈中，同时比较该元素和辅助栈的栈顶元素，若小于等于辅助栈栈顶元素，则将其也压入辅助栈中。

在弹出元素时，若该元素等于辅助栈的栈顶元素，则同时弹出该元素和辅助栈的栈顶元素。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
  8.  * 
  9.  * push(x) —— 将元素 x 推入栈中。
  10.  * pop() —— 删除栈顶的元素。
  11.  * top() —— 获取栈顶元素。
  12.  * getMin() —— 检索栈中的最小元素。
  13.  * @date 2023/4/8  22:29
  14.  */
  15. public class MinStack {
  16.     Stack stack = new Stack<>();
  17.     Stack minStack = new Stack<>();
  18.  
  19.     public MinStack() {
  20.     }
  21.  
  22.     public void push(int val) {
  23.         stack.push(val);
  24.         if (minStack.isEmpty() || val <= minStack.peek()) {
  25.             minStack.push(val);
  26.         }
  27.     }
  28.  
  29.     public void pop() {
  30.         if (stack.peek().equals(minStack.peek())) {
  31.             minStack.pop();
  32.         }
  33.         stack.pop();
  34.     }
  35.  
  36.     public int top() {
  37.         return stack.peek();
  38.     }
  39.  
  40.     public int getMin() {
  41.         return minStack.peek();
  42.     }
  43.  
  44.     public static void main(String[] args) {
  45.         /*验证最优解*/
  46.         MinStack minStack = new MinStack();
  47.         minStack.push(-2);
  48.         minStack.push(0);
  49.         minStack.push(-3);
  50.         /*-3*/
  51.         System.out.println(minStack.getMin());
  52.         minStack.pop();
  53.         /*0*/
  54.         System.out.println(minStack.top());
  55.         /*-2*/
  56.         System.out.println(minStack.getMin());
  57.     }
  58. }

（三）每日温度（Daily Temperatures）

题目描述：给定一个数组 T，求出 T 中每个元素与后面第一个比它大的元素之间的距离。

如果不存在这样的元素，则对应位置的值为 0。

例如，给定数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，应返回 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：每个温度值 T[i] 的范围是 [30, 100]。

解题思路

该问题可以使用单调栈来解决，单调栈的基本思路是维护一个栈，栈中的元素单调递减或递增。

对于本题，我们需要维护一个单调递减的栈，存储数组 T 中元素的下标，每次将一个元素压入栈中时，如果该元素比栈顶元素对应的元素大，则栈顶元素出栈，并且计算栈顶元素到该元素的距离，将距离存储到对应的结果数组中。直到该元素比栈顶元素小，将该元素入栈。

具体实现时，我们遍历数组 T，并将每个元素的下标入栈。当遇到一个比栈顶元素对应的元素大的元素时，我们可以通过栈顶元素的下标计算出距离，并将其存储到结果数组中。重复该过程直到遍历完整个数组。

时间复杂度为O(n)，其中n是数组 T 的长度。空间复杂度为O(n)。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Arrays;
  4. import java.util.Deque;
  5. import java.util.LinkedList;
  6.  
  7. /**
  8.  * @author yanfengzhang
  9.  * @description 给定一个数组 T，求出 T 中每个元素与后面第一个比它大的元素之间的距离。
  10.  * 
  11.  * 如果不存在这样的元素，则对应位置的值为 0。
  12.  * 例如，给定数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，应返回 [1, 1, 4, 2, 1, 1, 0, 0]。
  13.  * 提示：每个温度值 T[i] 的范围是 [30, 100]。
  14.  * @date 2023/4/8  22:39
  15.  */
  16. public class DailyTemperatures {
  17.  
  18.     /**
  19.      * 遍历数组 T，并将每个元素的下标入栈。
  20.      * 当遇到一个比栈顶元素对应的元素大的元素时，
  21.      * 我们可以通过栈顶元素的下标计算出距离，并将其存储到结果数组中。
  22.      * 重复该过程直到遍历完整个数组。
  23.      * 
  24.      * 时间复杂度为O(n)，其中n是数组 T 的长度。空间复杂度为O(n)。
  25.      */
  26.     public int[] dailyTemperatures(int[] T) {
  27.         int n = T.length;
  28.         int[] res = new int[n];
  29.         Deque stack = new LinkedList<>();
  30.         for (int i = 0; i < n; i++) {
  31.             while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
  32.                 int j = stack.pop();
  33.                 res[j] = i - j;
  34.             }
  35.             stack.push(i);
  36.         }
  37.         return res;
  38.     }
  39.  
  40.     public static void main(String[] args) {
  41.         int[] T = {73, 74, 75, 71, 69, 72, 76, 73};
  42.         int[] res = new DailyTemperatures().dailyTemperatures(T);
  43.         /*输出 [1, 1, 4, 2, 1, 1, 0, 0]*/
  44.         System.out.println(Arrays.toString(res));
  45.     }
  46. }

（四）用栈实现队列（Implement Queue using Stacks）

题目描述：使用栈实现队列，使得队列的操作 push、pop、peek、empty 的时间复杂度均为 O(1)

解题思路

两个栈实现队列的思路如下：

我们用两个栈stack1和stack2来模拟队列的操作。stack1负责入队列，stack2负责出队列。当我们需要入队列时，我们将元素压入stack1中；当需要出队列时，如果stack2为空，我们将stack1中的元素逐一弹出并压入stack2中，这样stack2中的元素就是按照队列先进先出的顺序排列。我们从stack2中弹出栈顶元素即可。

实现过程中，我们需要注意两点：

  1. 当stack2不为空时，不能将元素从stack1中压入stack2中，否则会打乱先进先出的顺序。
  2. 当stack1和stack2都为空时，队列为空，无法执行出队列操作，需要进行特殊处理。

综上所述，我们可以用两个栈来实现队列，时间复杂度为O(1)。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 使用栈实现队列，
  8.  * 使得队列的操作 push、pop、peek、empty 的时间复杂度均为 O(1)
  9.  * @date 2023/4/8  22:55
  10.  */
  11. public class ImplementQueueUseStacks {
  12.     static class MyQueue {
  13.         private Stack stack1;
  14.         private Stack stack2;
  15.  
  16.         /**
  17.          * Initialize your data structure here.
  18.          */
  19.         public MyQueue() {
  20.             stack1 = new Stack<>();
  21.             stack2 = new Stack<>();
  22.         }
  23.  
  24.         /**
  25.          * Push element x to the back of queue.
  26.          */
  27.         public void push(int x) {
  28.             stack1.push(x);
  29.         }
  30.  
  31.         /**
  32.          * Removes the element from in front of queue and returns that element.
  33.          */
  34.         public int pop() {
  35.             if (stack2.isEmpty()) {
  36.                 while (!stack1.isEmpty()) {
  37.                     stack2.push(stack1.pop());
  38.                 }
  39.             }
  40.             return stack2.pop();
  41.         }
  42.  
  43.         /**
  44.          * Get the front element.
  45.          */
  46.         public int peek() {
  47.             if (stack2.isEmpty()) {
  48.                 while (!stack1.isEmpty()) {
  49.                     stack2.push(stack1.pop());
  50.                 }
  51.             }
  52.             return stack2.peek();
  53.         }
  54.  
  55.         /**
  56.          * Returns whether the queue is empty.
  57.          */
  58.         public boolean empty() {
  59.             return stack1.isEmpty() && stack2.isEmpty();
  60.         }
  61.     }
  62.  
  63.     public static void main(String[] args) {
  64.         MyQueue queue = new MyQueue();
  65.  
  66.         queue.push(1);
  67.         queue.push(2);
  68.         /*输出 1 */
  69.         System.out.println(queue.peek());
  70.         /*输出 1 */
  71.         System.out.println(queue.pop());
  72.         /*输出 false */
  73.         System.out.println(queue.empty());
  74.     }
  75. }

（五）用队列实现栈（Implement Stack using Queues）

题目描述：使用队列实现栈的下列操作：

  • push(x) -- 元素 x 入栈
  • pop() -- 移除栈顶元素
  • top() -- 获取栈顶元素
  • empty() -- 返回栈是否为空

注意:

  • 你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
  • 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列，只要是标准的队列操作即可。

解题思路

使用两个队列实现栈，需要对其中一个队列进行逆序操作，这样每次出栈时都可以直接从逆序的队列中获取到栈顶元素，从而实现了栈的功能。

具体实现过程如下：

  • 定义两个队列，用来模拟栈的操作；
  • 入栈时，将元素插入队列1中；
  • 出栈时，将队列1中的元素依次取出并插入到队列2中，直到队列1中只剩下一个元素，然后将这个元素出队并返回；
  • 获取栈顶元素时，同样先将队列1中的元素依次取出并插入到队列2中，直到队列1中只剩下一个元素，然后返回这个元素；
  • 判断栈是否为空，即判断队列1和队列2是否都为空。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.LinkedList;
  4. import java.util.Queue;
  5.  
  6. /**
  7.  * @author yanfengzhang
  8.  * @description 使用队列实现栈的下列操作：
  9.  * 
  10.  * push(x) -- 元素 x 入栈
  11.  * pop() -- 移除栈顶元素
  12.  * top() -- 获取栈顶元素
  13.  * empty() -- 返回栈是否为空
  14.  * 注意:
  15.  * 你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
  16.  * 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列，只要是标准的队列操作即可。
  17.  * @date 2023/4/8  23:30
  18.  */
  19. public class ImplementStackUseQueues {
  20.  
  21.     static class MyStack {
  22.         private Queue q1;
  23.         private Queue q2;
  24.  
  25.         /**
  26.          * Initialize your data structure here.
  27.          */
  28.         public MyStack() {
  29.             q1 = new LinkedList<>();
  30.             q2 = new LinkedList<>();
  31.         }
  32.  
  33.         /**
  34.          * Push element x onto stack.
  35.          */
  36.         public void push(int x) {
  37.             q1.offer(x);
  38.             while (!q2.isEmpty()) {
  39.                 q1.offer(q2.poll());
  40.             }
  41.             Queue tmp = q1;
  42.             q1 = q2;
  43.             q2 = tmp;
  44.         }
  45.  
  46.         /**
  47.          * Removes the element on top of the stack and returns that element.
  48.          */
  49.         public int pop() {
  50.             return q2.poll();
  51.         }
  52.  
  53.         /**
  54.          * Get the top element.
  55.          */
  56.         public int top() {
  57.             return q2.peek();
  58.         }
  59.  
  60.         /**
  61.          * Returns whether the stack is empty.
  62.          */
  63.         public boolean empty() {
  64.             return q2.isEmpty();
  65.         }
  66.     }
  67.  
  68.  
  69.     public static void main(String[] args) {
  70.         MyStack myStack = new MyStack();
  71.  
  72.         myStack.push(1);
  73.         myStack.push(2);
  74.         myStack.push(3);
  75.  
  76.         /*3 */
  77.         System.out.println(myStack.pop());
  78.         /*2*/
  79.         System.out.println(myStack.top());
  80.         /*false*/
  81.         System.out.println(myStack.empty());
  82.  
  83.         myStack.pop();
  84.         myStack.pop();
  85.         /*true*/
  86.         System.out.println(myStack.empty());
  87.     }
  88. }

（六）接雨水（Trapping Rain Water）

题目描述：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能够捕获多少雨水。

解题思路

以下是使用栈实现的思路：

  1. 定义一个栈，并初始化为空。
  2. 遍历数组，如果当前元素小于等于栈顶元素，则将其下标压入栈中。
  3. 如果当前元素大于栈顶元素，则弹出栈顶元素，并计算雨水量：以弹出元素为高度，当前元素和栈顶元素所在位置之间的距离为宽度，宽度和高度求乘积得到雨水量。
  4. 计算完雨水量后，将当前元素下标入栈，重复步骤2和3，直到遍历完数组。
  5. 返回雨水总量。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，
  8.  * 计算按此排列的柱子，下雨之后能够捕获多少雨水
  9.  * @date 2023/4/8  23:48
  10.  */
  11. public class TrappingRainWater {
  12.  
  13.     /**
  14.      * 在这个实现中，我们首先定义了一个空栈和一个雨水总量的变量 water。
  15.      * 然后，我们遍历高度数组。对于每个高度，我们在栈不为空且当前高度大于栈顶元素高度的情况下，执行以下操作：
  16.      * 取出栈顶元素，作为坑洼的底部。
  17.      * 如果此时栈为空，则无法存储雨水，跳出循环。
  18.      * 计算坑洼的左右两侧边界。
  19.      * 根据左右两侧边界以及底部高度计算雨水量，并将其加入 water 变量中。
  20.      * 
  21.      * 在每次处理完高度后，我们将当前下标压入栈中，以便后续计算。最后，我们返回 water 变量即可。
  22.      */
  23.     public int trap(int[] height) {
  24.         Stack stack = new Stack<>();
  25.         int water = 0;
  26.         for (int i = 0; i < height.length; i++) {
  27.             while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
  28.                 /*取出栈顶元素作为坑洼的底部*/
  29.                 int bottom = stack.pop();
  30.                 /*如果栈为空，那么无法存储雨水，跳出循环*/
  31.                 if (stack.isEmpty()) {
  32.                     break;
  33.                 }
  34.                 /*计算坑洼的左右两侧边界*/
  35.                 int left = stack.peek();
  36.                 int right = i;
  37.                 /*根据左右两侧边界以及底部高度计算雨水量*/
  38.                 int width = right - left - 1;
  39.                 int heightDiff = Math.min(height[left], height[right]) - height[bottom];
  40.                 water += width * heightDiff;
  41.             }
  42.             /*将当前下标压入栈中*/
  43.             stack.push(i);
  44.         }
  45.         return water;
  46.     }
  47.  
  48.     /**
  49.      * 在这个示例中，我们将给定的高度数组设置为 height = {0,1,0,2,1,0,1,3,2,1,2,1} ，
  50.      * 期望的结果是能够计算出接到的雨水的总量。
  51.      * 调用 trap(height) 方法并将返回结果打印到控制台上，预期输出结果应该是 6。
  52.      */
  53.     public static void main(String[] args) {
  54.         int[] height = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
  55.         int res = new TrappingRainWater().trap(height);
  56.         /*输出结果应为6*/
  57.         System.out.println(res);
  58.     }
  59.  
  60.  
  61. }

（七）逆波兰表达式求值（Evaluate Reverse Polish Notation）

题目描述：逆波兰表达式（Reverse Polish Notation，简称RPN），也叫后缀表达式，是一种数学表达式的写法，其中运算符在操作数的后面。例如，将中缀表达式 3 + 4 * 2 / (1 - 5) 转换为逆波兰表达式的过程如下：3 4 2 * 1 5 - / +。

给定一个包含正整数、加减乘除符号以及空格的字符串 tokens，请你利用栈的思想，计算该表达式的值。

注意：

  • 整数除法仅保留整数部分。
  • 给定的 tokens 数组中，除数不为 0。
  • tokens 数组长度不超过 1000。

原题目出处：LeetCode链接

解题思路

该题的最优解法是使用栈数据结构，遍历表达式数组 tokens，遇到数字则将其压入栈中，遇到运算符则从栈中取出两个数字进行运算，然后将运算结果再次压入栈中。遍历完表达式数组后，栈顶元素即为表达式的计算结果。

具体算法如下：

  1. 初始化一个空栈 stack。
    • 遍历表达式数组 tokens，对于每一个元素 token：
    • 如果 token 是数字，则将其转换为整数并压入栈中。
    • 如果 token 是运算符，则从栈中取出两个数字进行运算，然后将运算结果再次压入栈中。
  2. 遍历完表达式数组后，栈顶元素即为表达式的计算结果。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 逆波兰表达式（Reverse Polish Notation，简称RPN），也叫后缀表达式，
  8.  * 是一种数学表达式的写法，其中运算符在操作数的后面。
  9.  * 例如，将中缀表达式 3 + 4 * 2 / (1 - 5) 转换为逆波兰表达式的过程如下：3 4 2 * 1 5 - / +。
  10.  * 
  11.  * 给定一个包含正整数、加减乘除符号以及空格的字符串 tokens，请你利用栈的思想，计算该表达式的值。
  12.  * @date 2023/4/8  23:56
  13.  */
  14. public class EvaluateReversePolishNotation {
  15.  
  16.     /**
  17.      * 最优解法是使用栈数据结构，遍历表达式数组 tokens，
  18.      * 遇到数字则将其压入栈中，遇到运算符则从栈中取出两个数字进行运算，
  19.      * 然后将运算结果再次压入栈中。遍历完表达式数组后，栈顶元素即为表达式的计算结果。
  20.      * 
  21.      * 具体算法如下：
  22.      * 初始化一个空栈 stack。
  23.      * 遍历表达式数组 tokens，对于每一个元素 token：
  24.      * 如果 token 是数字，则将其转换为整数并压入栈中。
  25.      * 如果 token 是运算符，则从栈中取出两个数字进行运算，然后将运算结果再次压入栈中。
  26.      * 遍历完表达式数组后，栈顶元素即为表达式的计算结果。
  27.      */
  28.     public int evalRPN(String[] tokens) {
  29.         /*初始化一个空栈*/
  30.         Stack stack = new Stack<>();
  31.         /*遍历表达式数组 tokens*/
  32.         for (String token : tokens) {
  33.             /*如果 token 是加号*/
  34.             if (token.equals("+")) {
  35.                 /*从栈中取出第二个数字*/
  36.                 int num2 = stack.pop();
  37.                 /*从栈中取出第一个数字*/
  38.                 int num1 = stack.pop();
  39.                 /*将两个数字相加，并将运算结果压入栈中*/
  40.                 stack.push(num1 + num2);
  41.             }
  42.             /*如果 token 是减号*/
  43.             else if (token.equals("-")) {
  44.                 /*从栈中取出第二个数字*/
  45.                 int num2 = stack.pop();
  46.                 /*从栈中取出第一个数字*/
  47.                 int num1 = stack.pop();
  48.                 /*将第一个数字减去第二个数字，并将运算结果压入栈中*/
  49.                 stack.push(num1 - num2);
  50.             }
  51.             /*如果 token 是乘号*/
  52.             else if (token.equals("*")) {
  53.                 /*从栈中取出第二个数字*/
  54.                 int num2 = stack.pop();
  55.                 /*从栈中取出第一个数字*/
  56.                 int num1 = stack.pop();
  57.                 /*将两个数字相乘，并将运算结果压入栈中*/
  58.                 stack.push(num1 * num2);
  59.             }
  60.             /*如果 token 是除号*/
  61.             else if (token.equals("/")) {
  62.                 /*从栈中取出第二个数字*/
  63.                 int num2 = stack.pop();
  64.                 /*从栈中取出第一个数字*/
  65.                 int num1 = stack.pop();
  66.                 /*将第一个数字除以第二个数字，并将运算结果压入栈中*/
  67.                 stack.push(num1 / num2);
  68.             }
  69.             /*如果 token 是数字*/
  70.             else {
  71.                 /*将其转换为整数并压入栈中*/
  72.                 stack.push(Integer.parseInt(token));
  73.             }
  74.         }
  75.         /*遍历完表达式数组后，栈顶元素即为表达式的计算结果*/
  76.         return stack.pop();
  77.     }
  78.  
  79.     public static void main(String[] args) {
  80.         String[] tokens1 = {"2", "1", "+", "3", "*"};
  81.         String[] tokens2 = {"4", "13", "5", "/", "+"};
  82.         String[] tokens3 = {"10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"};
  83.         /*expected output: 9*/
  84.         System.out.println(new EvaluateReversePolishNotation().evalRPN(tokens1));
  85.         /*expected output: 6*/
  86.         System.out.println(new EvaluateReversePolishNotation().evalRPN(tokens2));
  87.         /*expected output: 22*/
  88.         System.out.println(new EvaluateReversePolishNotation().evalRPN(tokens3));
  89.     }
  90. }

（八）基本计算器（Basic Calculator）

题目描述：实现一个基本的计算器来计算一个简单的字符串表达式的值。

表达式字符串可能包含左括号 ( 和右括号 )，加号 + 和减号 -，非负整数和空格。

示例 1:输入: "1 + 1".                              输出: 2

示例 2:输入: " 2-1 + 2 "                          输出: 3

示例 3:输入: "(1+(4+5+2)-3)+(6+8)".     输出: 23

注意:

你可以假设所给定的表达式都是有效的。

请不要使用内置的库函数 eval。

解题思路

使用栈存储数字和运算符，遇到括号则递归计算括号内的表达式。

  1. 初始化一个栈 stack 存储数字和运算符，和一个变量 res 存储结果，一个变量 sign 存储运算符的正负。
  2. 遍历表达式 s，如果当前字符是数字，用一个 while 循环读取整个数字并将其压入栈中；如果是加号，则将正号压入栈中，并将 sign 设为正；如果是减号，则将负号压入栈中，并将 sign 设为负；如果是左括号，则递归计算括号内的表达式，并将结果压入栈中；如果是右括号，则将栈顶的运算符弹出并计算到左括号，弹出左括号。
  3. 遍历完表达式后，将栈中剩余的数字和运算符依次弹出并计算结果。

时间复杂度：O(n)，其中n是表达式的长度。空间复杂度：O(n)。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description
  8.  * @date 2023/4/9  00:05
  9.  */
  10. public class BasicCalculator {
  11.  
  12.     /**
  13.      * 使用栈存储数字和运算符，遇到括号则递归计算括号内的表达式。
  14.      * 
  15.      * 1 初始化一个栈 stack 存储数字和运算符，和一个变量 res 存储结果，一个变量 sign 存储运算符的正负。
  16.      * 2 遍历表达式 s，如果当前字符是数字，用一个 while 循环读取整个数字并将其压入栈中；
  17.      * 如果是加号，则将正号压入栈中，并将 sign 设为正；
  18.      * 如果是减号，则将负号压入栈中，并将 sign 设为负；
  19.      * 如果是左括号，则递归计算括号内的表达式，并将结果压入栈中；
  20.      * 如果是右括号，则将栈顶的运算符弹出并计算到左括号，弹出左括号。
  21.      * 3 遍历完表达式后，将栈中剩余的数字和运算符依次弹出并计算结果。
  22.      */
  23.     public int calculate(String s) {
  24.         /*数字栈*/
  25.         Stack stack = new Stack<>();
  26.         /*当前数字*/
  27.         int num = 0;
  28.         /*当前结果*/
  29.         int result = 0;
  30.         /*符号，1表示加，-1表示减*/
  31.         int sign = 1;
  32.         for (char c : s.toCharArray()) {
  33.             /*如果当前字符是数字*/
  34.             if (Character.isDigit(c)) {
  35.                 /*将数字拼接起来*/
  36.                 num = num * 10 + (c - '0');
  37.             }
  38.             /*如果当前字符是加号*/
  39.             else if (c == '+') {
  40.                 /*先将之前的数字和符号加入结果中*/
  41.                 result += sign * num;
  42.                 /*重置当前数字*/
  43.                 num = 0;
  44.                 /*设置符号为加*/
  45.                 sign = 1;
  46.             }
  47.             /*如果当前字符是减号*/
  48.             else if (c == '-') {
  49.                 /*先将之前的数字和符号加入结果中*/
  50.                 result += sign * num;
  51.                 /*重置当前数字*/
  52.                 num = 0;
  53.                 /*设置符号为减*/
  54.                 sign = -1;
  55.             }
  56.             /*如果当前字符是左括号*/
  57.             else if (c == '(') {
  58.                 /*将当前结果入栈*/
  59.                 stack.push(result);
  60.                 /*将当前符号入栈*/
  61.                 stack.push(sign);
  62.                 /*重置当前结果*/
  63.                 result = 0;
  64.                 /*重置当前符号*/
  65.                 sign = 1;
  66.             }
  67.             /*如果当前字符是右括号*/
  68.             else if (c == ')') {
  69.                 /*先将当前数字加入结果中*/
  70.                 result += sign * num;
  71.                 /*重置当前数字*/
  72.                 num = 0;
  73.                 /*取出栈顶符号乘以当前结果*/
  74.                 result *= stack.pop();
  75.                 /*加上栈顶数字*/
  76.                 result += stack.pop();
  77.             }
  78.         }
  79.         /*处理最后一个数字*/
  80.         if (num != 0) {
  81.             result += sign * num;
  82.         }
  83.         return result;
  84.     }
  85.  
  86.     public static void main(String[] args) {
  87.         String s = "1 + (2 - 3) + 4";
  88.         int result = new BasicCalculator().calculate(s);
  89.         /*输出4*/
  90.         System.out.println(result);
  91.     }
  92.  
  93. }

（九）简化路径（Simplify Path）

题目描述：给定一个字符串路径，返回其简化的绝对路径。

例如，path = "/home/", => "/home"；path = "/../", => "/"；path = "/home//foo/", => "/home/foo"；path = "/a/./b/../../c/", => "/c"

在简化路径时，要考虑以下规则：

1.路径是由斜杠'/'分隔的一个或多个目录或文件名组成的。

2.在Unix风格的文件系统中，'.'表示当前目录，'..'表示上一级目录。

3.如果路径中包含多个连续斜杠'/'，则应将它们替换为一个单独的斜杠'/'。

4.路径应以斜杠'/'开头，并且在路径末尾不应该有斜杠'/'。

请注意，返回的简化路径必须始终以斜杠'/'开头，并且在路径末尾不能有斜杠'/'。

解题思路

最优解法是使用栈。具体做法如下：

  1. 以“/”作为分隔符，将输入路径拆分成若干个部分。
    • 遍历这些部分：
    • 如果部分为空或为“.””，则不做处理，继续遍历下一个部分。
    • 如果部分为“..”，则将栈顶元素弹出，表示返回上级目录。
    • 否则，将部分压入栈中，表示进入下一级目录。
  2. 遍历完所有部分后，将栈中的元素按顺序拼接起来，得到简化后的路径。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 给定一个字符串路径，返回其简化的绝对路径。
  8.  * 例如，path = "/home/", => "/home"；path = "/../", => "/"；
  9.  * path = "/home//foo/", => "/home/foo"；
  10.  * path = "/a/./b/../../c/", => "/c"
  11.  * @date 2023/4/9  00:17
  12.  */
  13. public class SimplifyPath {
  14.  
  15.     /**
  16.      * 最优解法是使用栈。具体做法如下：
  17.      * 
  18.      * 1 以“/”作为分隔符，将输入路径拆分成若干个部分。
  19.      * 遍历这些部分：
  20.      * 如果部分为空或为“.””，则不做处理，继续遍历下一个部分。
  21.      * 如果部分为“..”，则将栈顶元素弹出，表示返回上级目录。
  22.      * 否则，将部分压入栈中，表示进入下一级目录。
  23.      * 2 遍历完所有部分后，将栈中的元素按顺序拼接起来，得到简化后的路径。
  24.      */
  25.     public String simplifyPath(String path) {
  26.         Stack stack = new Stack<>();
  27.         String[] arr = path.split("/");
  28.         for (String s : arr) {
  29.             if (s.equals(".") || s.equals("")) {
  30.                 /*对于"."和空字符串，不做任何操作*/
  31.             } else if (s.equals("..")) {
  32.                 /*如果是"..", 则需要返回上一级目录*/
  33.                 if (!stack.isEmpty()) {
  34.                     stack.pop();
  35.                 }
  36.             } else {
  37.                 /*否则就是一个普通的路径名，需要入栈*/
  38.                 stack.push(s);
  39.             }
  40.         }
  41.  
  42.         /*构造简化后的路径*/
  43.         StringBuilder sb = new StringBuilder();
  44.         for (String s : stack) {
  45.             sb.append("/").append(s);
  46.         }
  47.  
  48.         /*如果栈为空，说明简化后的路径是根路径"/" */
  49.         if (stack.isEmpty()) {
  50.             return "/";
  51.         }
  52.  
  53.         return sb.toString();
  54.     }
  55.  
  56.     public static void main(String[] args) {
  57.         String path = "/a//b/../../c/";
  58.         /*输出：/c */
  59.         System.out.println(new SimplifyPath().simplifyPath(path));
  60.     }
  61. }

(十) 岛屿数量

题目描述：给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

 提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • grid[i][j] 的值为 '0' 或 '1'

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/number-of-islands

解法思路

使用栈的解法可以通过深度优先搜索（DFS）来实现。遍历矩阵中每一个元素，对于每一个为1的元素，将其作为起点，进行DFS遍历并将经过的元素标记为0，统计遍历的次数即为岛屿的数量。具体实现思路如下：

  1. 遍历矩阵中的每个元素，当元素为1时，进入DFS遍历。
  2. 进入DFS遍历时，将当前元素标记为0，表示已经遍历过。
  3. 遍历当前元素的四个方向（上、下、左、右），如果该方向上的元素为1，则进入该方向继续DFS遍历。
  4. 当所有与当前元素相连通的元素都被遍历过后，回到上一个节点继续遍历。
  5. 统计遍历的次数即为岛屿的数量。

这种解法的时间复杂度为O(mn)，其中m和n分别为矩阵的行数和列数。空间复杂度为O(mn)，因为需要使用一个二维数组来标记每个元素是否已经遍历过。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 给你一个由'1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。
  8.  * 岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
  9.  * 此外，你可以假设该网格的四条边均被水包围。
  10.  * @date 2023/4/9  15:35
  11.  */
  12. public class NumIslands {
  13.  
  14.     /**
  15.      * 具体实现思路如下：
  16.      * 
  17.      * 遍历矩阵中的每个元素，当元素为1时，进入DFS遍历。
  18.      * 进入DFS遍历时，将当前元素标记为0，表示已经遍历过。
  19.      * 遍历当前元素的四个方向（上、下、左、右），如果该方向上的元素为1，则进入该方向继续DFS遍历。
  20.      * 当所有与当前元素相连通的元素都被遍历过后，回到上一个节点继续遍历。
  21.      * 统计遍历的次数即为岛屿的数量。
  22.      */
  23.     public int numIslands(char[][] grid) {
  24.         /*记录岛屿数量*/
  25.         int count = 0;
  26.         int m = grid.length;
  27.         if (m == 0) {
  28.             return 0;
  29.         }
  30.         int n = grid[0].length;
  31.         /*方向数组，用于四个方向的遍历*/
  32.         int[] dx = {0, 0, 1, -1};
  33.         int[] dy = {1, -1, 0, 0};
  34.         /*记录当前位置是否已经被访问*/
  35.         boolean[][] visited = new boolean[m][n];
  36.         /*用栈来模拟深度优先搜索*/
  37.         Stack<int[]> stack = new Stack<>();
  38.         for (int i = 0; i < m; i++) {
  39.             for (int j = 0; j < n; j++) {
  40.                 /*如果当前位置是陆地且没有被访问过*/
  41.                 if (grid[i][j] == '1' && !visited[i][j]) {
  42.                     /*岛屿数量+1*/
  43.                     count++;
  44.                     /*将当前位置入栈*/
  45.                     stack.push(new int[]{i, j});
  46.                     /*标记当前位置为已访问*/
  47.                     visited[i][j] = true;
  48.                     /*栈不为空时继续搜索*/
  49.                     while (!stack.empty()) {
  50.                         /*取出栈顶元素作为当前位置*/
  51.                         int[] cur = stack.pop();
  52.                         /*四个方向遍历*/
  53.                         for (int k = 0; k < 4; k++) {
  54.                             int x = cur[0] + dx[k];
  55.                             int y = cur[1] + dy[k];
  56.                             /*如果满足条件，则入栈并标记为已访问*/
  57.                             if (x >= 0 && x < m && y >= 0
  58.                                     && y < n
  59.                                     && !visited[x][y]
  60.                                     && grid[x][y] == '1') {
  61.                                 stack.push(new int[]{x, y});
  62.                                 visited[x][y] = true;
  63.                             }
  64.                         }
  65.                     }
  66.                 }
  67.             }
  68.         }
  69.         return count;
  70.     }
  71.  
  72.      public static void main(String[] args) {
  73.         char[][] grid = {
  74.                 {'1', '1', '0', '0', '0'},
  75.                 {'1', '1', '0', '0', '0'},
  76.                 {'0', '0', '1', '0', '0'},
  77.                 {'0', '0', '0', '1', '1'}
  78.         };
  79.         int numIslands = new NumIslands().numIslands(grid);
  80.         /*输出 3*/
  81.         System.out.println(numIslands); 
  82.     }
  83.  
  84. }

扩展：其他最优解法展示

思路

该问题可以通过深度优先搜索（DFS）或广度优先搜索（BFS）来解决。下面以DFS为例，介绍最优解法思路：

  • 遍历整个二维网格，当发现一个为 '1' 的点时，从这个点开始进行 DFS。在 DFS 过程中，将访问到的 '1' 置为 '0'，防止重复访问。同时，沿着当前点的上下左右四个方向继续深入搜索。
  • 深度优先搜索结束后，岛屿的数量加1。继续遍历网格，如果发现下一个点为 '1'，则进行新一轮 DFS。
  • 遍历完整个网格后，就可以得到岛屿的数量。

可以用递归或显式的栈来实现 DFS，具体实现方式因人而异。

时间复杂度为 O(mn)，其中 m 和 n 分别为网格的行数和列数。

代码展示

以下是基于DFS实现的Java代码，其中用 visited 数组记录每个点是否已经被访问过，从一个点开始搜索时，将其 visited 数组值设为 true，表示已经访问过。在 DFS 中，每次向四个方向递归搜索时，需要先检查坐标是否合法，并且当前点是否为 '1'。如果坐标合法且当前点为 '1'，则将其 visited 数组值设为 true，并继续向四个方向递归搜索。

  1. public int numIslands(char[][] grid) {
  2.             /*边界条件判断*/
  3.             if (grid == null || grid.length == 0) {
  4.                 return 0;
  5.             }
  6.             int m = grid.length;
  7.             int n = grid[0].length;
  8.             /*记录每个点是否已经被访问过*/
  9.             boolean[][] visited = new boolean[m][n];
  10.             /*岛屿数量计数器*/
  11.             int count = 0;
  12.             /*遍历整个网格*/
  13.             for (int i = 0; i < m; i++) {
  14.                 for (int j = 0; j < n; j++) {
  15.                     /*如果当前点为 '1' 且未被访问过，说明发现一个新的岛屿，需要进行 DFS 搜索*/
  16.                     if (!visited[i][j] && grid[i][j] == '1') {
  17.                         /*岛屿数量加1*/
  18.                         count++;
  19.                         /*从当前点开始进行 DFS 搜索*/
  20.                         dfs(grid, visited, i, j);
  21.                     }
  22.                 }
  23.             }
  24.             /*返回岛屿数量*/
  25.             return count;
  26.         }
  27.  
  28.         private void dfs(char[][] grid, boolean[][] visited, int i, int j) {
  29.             /*如果坐标不合法，或当前点已被访问过，或当前点为 '0'，则直接返回*/
  30.             if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || visited[i][j] || grid[i][j] == '0') {
  31.                 return;
  32.             }
  33.             /*将当前点标记为已访问*/
  34.             visited[i][j] = true;
  35.             /*分别向上、下、左、右四个方向递归搜索*/
  36.             /*上*/
  37.             dfs(grid, visited, i - 1, j);
  38.             /*下*/
  39.             dfs(grid, visited, i + 1, j);
  40.             /*左*/
  41.             dfs(grid, visited, i, j - 1);
  42.             /*右*/
  43.             dfs(grid, visited, i, j + 1);
  44.         }

（十一）用数组实现一个栈

题目描述：设计一个栈数据结构，使用数组来实现。需要支持入栈、出栈、获取栈顶元素和判断栈是否为空的操作。

解题思路

基本解题思路如下：

  1. 创建一个数组 stack 用于存储栈中的元素。
  2. 维护一个变量 top 表示栈顶的索引位置，初始值为 -1。
  3. 入栈操作：将要入栈的元素放入 stack 数组中 top+1 的位置，然后将 top 的值加 1。
  4. 出栈操作：从 stack 数组中取出 top 位置的元素，然后将 top 的值减 1。
  5. 获取栈顶元素操作：返回 stack 数组中 top 位置的元素。
  6. 判断栈是否为空操作：当 top 的值为 -1 时，表示栈为空。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. /**
  4.  * @author yanfengzhang
  5.  * @description 设计一个栈数据结构，使用数组来实现。
  6.  * 需要支持入栈、出栈、获取栈顶元素和判断栈是否为空的操作。
  7.  *
  8.  * 解题思路：
  9.  * 	1.	创建一个数组 stack 用于存储栈中的元素。
  10.  * 	2.	维护一个变量 top 表示栈顶的索引位置，初始值为 -1。
  11.  * 	3.	入栈操作：将要入栈的元素放入 stack 数组中 top+1 的位置，然后将 top 的值加 1。
  12.  * 	4.	出栈操作：从 stack 数组中取出 top 位置的元素，然后将 top 的值减 1。
  13.  * 	5.	获取栈顶元素操作：返回 stack 数组中 top 位置的元素。
  14.  * 	6.	判断栈是否为空操作：当 top 的值为 -1 时，表示栈为空。
  15.  * @date 2023/6/14  23:28
  16.  */
  17. public class ImplementStackUseArray {
  18.     private int[] stack;
  19.     private int top;
  20.  
  21.     public ImplementStackUseArray(int capacity) {
  22.         stack = new int[capacity];
  23.         /*将 top 初始化为 -1*/
  24.         top = -1;
  25.     }
  26.  
  27.     /**
  28.      * push(int element) 方法用于将元素入栈，
  29.      * 它首先检查栈是否已满，
  30.      * 然后将元素放入 top+1 的位置，
  31.      * 最后将 top 的值加 1。
  32.      * @param element
  33.      */
  34.     public void push(int element) {
  35.         if (top == stack.length - 1) {
  36.             throw new IllegalStateException("Stack is full");
  37.         }
  38.         stack[++top] = element;
  39.     }
  40.  
  41.     /**
  42.      * pop() 方法用于出栈，
  43.      * 它首先检查栈是否为空，
  44.      * 然后返回 top 位置的元素，
  45.      * 最后将 top 的值减 1。
  46.      * @return
  47.      */
  48.     public int pop() {
  49.         if (isEmpty()) {
  50.             throw new IllegalStateException("Stack is empty");
  51.         }
  52.         return stack[top--];
  53.     }
  54.  
  55.     /**
  56.      * peek() 方法用于获取栈顶元素，
  57.      * 它首先检查栈是否为空，然后返回 top 位置的元素。
  58.      * @return
  59.      */
  60.     public int peek() {
  61.         if (isEmpty()) {
  62.             throw new IllegalStateException("Stack is empty");
  63.         }
  64.         return stack[top];
  65.     }
  66.  
  67.     /**
  68.      * isEmpty() 方法用于判断栈是否为空，
  69.      * 它通过判断 top 的值是否为 -1 来确定
  70.      * @return
  71.      */
  72.     public boolean isEmpty() {
  73.         return top == -1;
  74.     }
  75.  
  76.     public static void main(String[] args) {
  77.         ImplementStackUseArray stack = new ImplementStackUseArray(5);
  78.  
  79.         stack.push(10);
  80.         stack.push(20);
  81.         stack.push(30);
  82.  
  83.         // 输出 Top element: 30
  84.         System.out.println("Top element: " + stack.peek());
  85.  
  86.         // 输出 Popped element: 30
  87.         System.out.println("Popped element: " + stack.pop());
  88.  
  89.         // 输出 Top element after pop: 20
  90.         System.out.println("Top element after pop: " + stack.peek());
  91.  
  92.         // 输出 Is stack empty? false
  93.         System.out.println("Is stack empty? " + stack.isEmpty());
  94.     }
  95. }

（十二）基本数学运算表达式求值

题目描述：给定一个包含加法、减法、乘法和除法的算术表达式字符串，设计一个程序来计算其结果。也就是说给个1+2*5-6\2字符串，最后计算出来就行

解题思路

要计算一个包含加减乘除的算术表达式，可以使用栈（Stack）数据结构来辅助计算。以下是一种常见的解题思路：

  1. 创建两个栈，一个用于存储操作数（Operand Stack），一个用于存储运算符（Operator Stack）。
  2. 从左到右依次遍历表达式的每个字符。
  3. 如果当前字符是数字，则将其解析为操作数，并将操作数入栈到 Operand Stack。
  4. 如果当前字符是运算符，则执行以下步骤：a. 如果 Operator Stack 为空，或者栈顶运算符是左括号 ‘(’，则将当前运算符入栈到 Operator Stack。 b. 如果当前运算符优先级大于栈顶运算符优先级，或者栈顶运算符是左括号 ‘(’，则将当前运算符入栈到 Operator Stack。 c. 否则，从 Operator Stack 弹出栈顶运算符，从 Operand Stack 弹出两个操作数，进行相应的计算，并将结果入栈到 Operand Stack。重复该步骤直到满足条件 b，然后将当前运算符入栈到 Operator Stack。注意：在比较运算符优先级时，可以使用一定的约定，例如将加法和减法设定为优先级较低，乘法和除法设定为优先级较高。
  5.  如果当前字符是左括号 ‘(’，则将其入栈到 Operator Stack。
  6. 如果当前字符是右括号 ‘)’，则执行以下步骤： 从 Operator Stack 弹出栈顶运算符，从 Operand Stack 弹出两个操作数，进行相应的计算，并将结果入栈到 Operand Stack。重复该步骤直到遇到左括号 ‘(’，将其从 Operator Stack 弹出并丢弃。
  7. 遍历完表达式后，执行以下步骤：a. 如果 Operator Stack 不为空，则从 Operator Stack 弹出栈顶运算符，从 Operand Stack 弹出两个操作数，进行相应的计算，并将结果入栈到 Operand Stack。重复该步骤直到 Operator Stack 为空。b. 最后 Operand Stack 中剩下的唯一元素就是表达式的最终结果。

具体代码展示

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import java.util.Stack;
  4.  
  5. /**
  6.  * @author yanfengzhang
  7.  * @description 给定一个包含加法、减法、乘法和除法的算术表达式字符串，设计一个程序来计算其结果。
  8.  * @date 2023/6/13  23:29
  9.  */
  10. public class ArithmeticExpressionCalculator {
  11.  
  12.     /**
  13.      *
  14.      * 要计算一个包含加减乘除的算术表达式，可以使用栈（Stack）数据结构来辅助计算。以下是一种常见的解题思路：
  15.      * 	1.	创建两个栈，一个用于存储操作数（Operand Stack），一个用于存储运算符（Operator Stack）。
  16.      * 	2.	从左到右依次遍历表达式的每个字符。
  17.      * 	3.	如果当前字符是数字，则将其解析为操作数，并将操作数入栈到 Operand Stack。
  18.      * 	4.	如果当前字符是运算符，则执行以下步骤：
  19.      * 	•	a. 如果 Operator Stack 为空，或者栈顶运算符是左括号 ‘(’，则将当前运算符入栈到 Operator Stack。
  20.      * 	•	b. 如果当前运算符优先级大于栈顶运算符优先级，或者栈顶运算符是左括号 ‘(’，则将当前运算符入栈到 Operator Stack。
  21.      * 	•	c. 否则，从 Operator Stack 弹出栈顶运算符，从 Operand Stack 弹出两个操作数，进行相应的计算，并将结果入栈到 Operand Stack。重复该步骤直到满足条件 b，然后将当前运算符入栈到 Operator Stack。
  22.      * 	•	注意：在比较运算符优先级时，可以使用一定的约定，例如将加法和减法设定为优先级较低，乘法和除法设定为优先级较高。
  23.      * 	5.	如果当前字符是左括号 ‘(’，则将其入栈到 Operator Stack。
  24.      * 	6.	如果当前字符是右括号 ‘)’，则执行以下步骤：
  25.      * 	•	a. 从 Operator Stack 弹出栈顶运算符，从 Operand Stack 弹出两个操作数，进行相应的计算，并将结果入栈到 Operand Stack。重复该步骤直到遇到左括号 ‘(’，将其从 Operator Stack 弹出并丢弃。
  26.      * 	7.	遍历完表达式后，执行以下步骤：
  27.      * 	•	a. 如果 Operator Stack 不为空，则从 Operator Stack 弹出栈顶运算符，从 Operand Stack 弹出两个操作数，进行相应的计算，并将结果入栈到 Operand Stack。重复该步骤直到 Operator Stack 为空。
  28.      * 	•	b. 最后 Operand Stack 中剩下的唯一元素就是表达式的最终结果。
  29.      * @param expression
  30.      * @return
  31.      */
  32.     public static int calculate(String expression) {
  33.         Stack operandStack = new Stack<>();
  34.         Stack operatorStack = new Stack<>();
  35.  
  36.         for (int i = 0; i < expression.length(); i++) {
  37.             char ch = expression.charAt(i);
  38.             if (Character.isDigit(ch)) {
  39.                 // 当前字符是数字，将其解析为操作数并入栈
  40.                 // 将字符转换为整数
  41.                 int operand = ch - '0';
  42.                 while (i + 1 < expression.length()
  43.                         && Character.isDigit(expression.charAt(i + 1))) {
  44.                     // 继续读取多位数字
  45.                     operand = operand * 10 + (expression.charAt(i + 1) - '0');
  46.                     i++;
  47.                 }
  48.                 operandStack.push(operand);
  49.             } else if (ch == '(') {
  50.                 // 当前字符是左括号，入栈到运算符栈
  51.                 operatorStack.push(ch);
  52.             } else if (ch == ')') {
  53.                 // 当前字符是右括号，执行计算直到遇到左括号
  54.                 while (!operatorStack.isEmpty() && operatorStack.peek() != '(') {
  55.                     calculateTopOperation(operandStack, operatorStack);
  56.                 }
  57.                 // 弹出左括号 '('
  58.                 if (!operatorStack.isEmpty() && operatorStack.peek() == '(') {
  59.                     operatorStack.pop();
  60.                 }
  61.             } else if (ch == '+' || ch == '-' || ch == '*' || ch == '/') {
  62.                 // 当前字符是运算符
  63.                 while (!operatorStack.isEmpty()
  64.                         && shouldEvaluateTopOperation(ch, operatorStack.peek())) {
  65.                     calculateTopOperation(operandStack, operatorStack);
  66.                 }
  67.                 operatorStack.push(ch);
  68.             }
  69.         }
  70.  
  71.         // 执行剩余的计算
  72.         while (!operatorStack.isEmpty()) {
  73.             calculateTopOperation(operandStack, operatorStack);
  74.         }
  75.  
  76.         // 最后 Operand Stack 中剩下的唯一元素就是表达式的最终结果
  77.         return operandStack.pop();
  78.     }
  79.  
  80.     private static boolean shouldEvaluateTopOperation(char currentOperator, char topOperator) {
  81.         if (topOperator == '(' || topOperator == ')') {
  82.             return false;
  83.         }
  84.         if ((currentOperator == '*' || currentOperator == '/')
  85.                 && (topOperator == '+' || topOperator == '-')) {
  86.             return false;
  87.         }
  88.         return true;
  89.     }
  90.  
  91.     private static void calculateTopOperation(Stack operandStack, Stack operatorStack) {
  92.         char operator = operatorStack.pop();
  93.         int operand2 = operandStack.pop();
  94.         int operand1 = operandStack.pop();
  95.         int result = 0;
  96.         switch (operator) {
  97.             case '+':
  98.                 result = operand1 + operand2;
  99.                 break;
  100.             case '-':
  101.                 result = operand1 - operand2;
  102.                 break;
  103.             case '*':
  104.                 result = operand1 * operand2;
  105.                 break;
  106.             case '/':
  107.                 result = operand1 / operand2;
  108.                 break;
  109.         }
  110.         operandStack.push(result);
  111.     }
  112.  
  113.     public static void main(String[] args) {
  114.         String expression1 = "1+2*5-6/2";
  115.         int result1 = calculate(expression1);
  116.         System.out.println(expression1 + "=" + result1);
  117.  
  118.         String expression2 = "1 + (2 - 3) + 4";
  119.         int result2 = calculate(expression2);
  120.         System.out.println(expression2 + "=" + result2);
  121.     }
  122. }

（十三） IP 范围判断

题目描述：给定一个二叉树，每个节点包含一个 IP 段的范围，其中 ip1 和 ip2 分别表示左子树和右子树的 IP 范围。现在给定一个 IP 地址，判断该 IP 是否在任意节点的 IP 范围内。

解题思路

为了判断一个 IP 地址是否在二叉树的某个节点的 IP 范围内，我们可以采用非递归的方式进行树的遍历，并在遍历过程中进行比较。以下是一种可能的解法：

  1. 定义一个栈 stack，用于存储待遍历的节点。
  2. 将根节点入栈。
  3. 循环遍历栈，直到栈为空：• 弹出栈顶节点 node。• 判断当前 IP 地址是否在 node 的 IP 范围内。如果在范围内，则返回 true。• 如果 node 的左子节点不为空且当前 IP 小于等于左子节点的 IP 范围的最大值，将左子节点入栈。• 如果 node 的右子节点不为空且当前 IP 大于等于右子节点的 IP 范围的最小值，将右子节点入栈。
  4. 如果遍历完整个树，仍未找到匹配的 IP 范围，则返回 false。

通过以上方法，我们可以判断给定的 IP 地址是否在二叉树的任意节点的 IP 范围内。该算法的时间复杂度取决于树的深度，最坏情况下为 O(n)，其中 n 是树中节点的个数。

具体代码展示

先初始化定义IP树节点如下：

  1. package org.zyf.javabasic.letcode.stack.base;
  2.  
  3. /**
  4.  * @author yanfengzhang
  5.  * @description
  6.  * @date 2023/6/11  23:54
  7.  */
  8. public class IPTreeNode {
  9.     public String ip1;
  10.     public String ip2;
  11.     public IPTreeNode left;
  12.     public IPTreeNode right;
  13.  
  14.     public IPTreeNode(String ip1, String ip2) {
  15.         this.ip1 = ip1;
  16.         this.ip2 = ip2;
  17.     }
  18. }

具体代码分析展示如下：

  1. package org.zyf.javabasic.letcode.stack;
  2.  
  3. import org.zyf.javabasic.letcode.stack.base.IPTreeNode;
  4.  
  5. import java.util.Stack;
  6.  
  7. /**
  8.  * @author yanfengzhang
  9.  * @description 给定一个二叉树，每个节点包含一个 IP 段的范围，其中 ip1 和 ip2 分别表示左子树和右子树的 IP 范围。
  10.  * 现在给定一个 IP 地址，判断该 IP 是否在任意节点的 IP 范围内。
  11.  * @date 2023/6/11  00:09
  12.  */
  13. public class IPAddressRange {
  14.     public boolean isIPInRange(IPTreeNode root, String ip) {
  15.         if (root == null || ip == null) {
  16.             return false;
  17.         }
  18.  
  19.         Stack stack = new Stack<>();
  20.         stack.push(root);
  21.  
  22.         while (!stack.isEmpty()) {
  23.             IPTreeNode node = stack.pop();
  24.  
  25.             if (isIPInRange(ip, node.ip1, node.ip2)) {
  26.                 return true;
  27.             }
  28.  
  29.             if (node.left != null) {
  30.                 stack.push(node.left);
  31.             }
  32.  
  33.             if (node.right != null) {
  34.                 stack.push(node.right);
  35.             }
  36.         }
  37.  
  38.         return false;
  39.     }
  40.  
  41.     private boolean isIPInRange(String ip, String startIP, String endIP) {
  42.         long ipValue = ipToLong(ip);
  43.         long startValue = ipToLong(startIP);
  44.         long endValue = ipToLong(endIP);
  45.  
  46.         return ipValue >= startValue && ipValue <= endValue;
  47.     }
  48.  
  49.     private long ipToLong(String ip) {
  50.         String[] parts = ip.split("\\.");
  51.         long result = 0;
  52.  
  53.         for (int i = 0; i < 4; i++) {
  54.             result = result * 256 + Long.parseLong(parts[i]);
  55.         }
  56.  
  57.         return result;
  58.     }
  59.  
  60.     public static void main(String[] args) {
  61.         IPTreeNode root = new IPTreeNode("192.168.0.1", "192.168.0.100");
  62.         root.left = new IPTreeNode("10.0.0.1", "10.0.0.10");
  63.         root.right = new IPTreeNode("172.16.0.1", "172.16.0.50");
  64.  
  65.         IPAddressRange solution = new IPAddressRange();
  66.         String ip = "10.0.0.5";
  67.         boolean isInRange = solution.isIPInRange(root, ip);
  68.         // 输出 10.0.0.5 is in range: true
  69.         System.out.println(ip + " is in range: " + isInRange);
  70.     }
  71. }

文章知识点与官方知识档案匹配，可进一步学习相关知识
算法技能树首页概览62532 人正在系统学习中
注：本文转载自blog.csdn.net的张彦峰ZYF的文章"https://blog.csdn.net/xiaofeng10330111/article/details/127557152"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！