朴素贝叶斯原理：

虽然决策树抽象出了规则，方便了人的理解，但是严格按照决策树来判断新朋友能否成为好朋友感觉很困难，这个可能性能够把握吗？比如我和TA有80%的可能成为好朋友。又或者能将我的朋友们分为“三六九等”吗？即，多分类问题。今天总结–和决策树一样被最为广泛应用的朴素贝叶斯模型。

先上贝叶斯定理：
$$P(X|Y)=\frac{P(X,Y)}{P(Y)}$$
$$P(Y|X)=\frac{P(X,Y)}{P(X)}$$
由条件概率很容易看出：$$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)}$$
更一般的写法为：$$P(Y_i|X)=\frac{P(X|Y_i)P(Y_i)}{\sum _{i}P(X|Y=Y_i)P(Y_i)}$$

从贝叶斯定理出发，很容易想到基于它来估计后验概率P(Y|X)。但是P(X|Y)是所有属性上的联合概率，难以从有限的数据集中直击估计，为此“朴素”贝叶斯采用了条件独立性假设：假设所有属性相互独立。此时有：$$P(X,Y)=P(X)P(Y)$$
贝叶斯可重写为：
$$h_{nb}(x)={argmax}_{C_k}P(Y)\prod _{i=1}^{n}P(X_i|Y),其中n为属性数目$$
$$那么显然基于训练集来估计类先验概率P（Y），并为每个属性估计出条件概率P（X_i|Y）即可训练好贝叶斯分类器了$$那么由此可以做一个很重要的文本分类的简单模型了。

算法实现：（Python）

from numpy import *
def loadDataSet():#文本词表转换到向量
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]#标记是否是侮辱性的句子
    return postingList,classVec
                 
def createVocabList(dataSet):
    vocabSet = set([])  
    for document in dataSet:
        vocabSet = vocabSet | set(document) #集合的并集，目的是使词不重复
    return list(vocabSet)

def setOfWords2Vec(vocabList, inputSet):#词集模型，输入参数为词汇表和某文档。记录文档词是否在词汇表中，便于之后的使用。
    returnVec = [0]*len(vocabList)
    for word in inputSet:#遍历每个词
        if word in vocabList:#只是记录“存在”，默认词之间无差别，即只设1不累计
            returnVec[vocabList.index(word)] = 1
        else: print ("the word: %s is not in my Vocabulary!" % word)
    return returnVec

def bagOfWords2VecMN(vocabList, inputSet):#词袋模型，改进函数setOfWords2Vec。出现多次的词可能有某种意味。
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:#使用加和
            returnVec[vocabList.index(word)] += 1
    return returnVec

def trainNB0(trainMatrix,trainCategory):#输入为文档矩阵和标签。输出概率
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory)/float(numTrainDocs)
    p0Num = ones(numWords); p1Num = ones(numWords)  #防止累乘之后为0，所有词出现数初始化为1
    p0Denom = 2.0; p1Denom = 2.0#防止累乘之后为0，分母初始化为2
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:#遍历文档，只要属于1的出现就累积
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = log(p1Num/p1Denom)  #出现数除以总词数
    p0Vect = log(p0Num/p0Denom) #用了log防止很多小数相乘而导致下溢或者出现不正确的答案。
    return p0Vect,p1Vect,pAbusive#每个类别的条件概率

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):#要分类的向量和上面函数算出的三个概率
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)  
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else: 
        return 0

def testingNB():#便利函数，用于测试
    listOPosts,listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat=[]
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print (testEntry,'类别是 ',classifyNB(thisDoc,p0V,p1V,pAb))
    testEntry = ['stupid', 'garbage']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print (testEntry,'类别是 ',classifyNB(thisDoc,p0V,p1V,pAb))

testingNB()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

[‘love’, ‘my’, ‘dalmation’] 类别是 0
[‘stupid’, ‘garbage’] 类别是 1

同样的，我们来探讨一下出现问题。

有些概率怎么为0了？Laplace校准。
由于某些属性在训练集中可能没有与某个类别同时出现过，那么计算时P（a|y）=0，这显然不太合理，结果的准确自然也是大大降低的。为了避免这种现象出现，所以引入了Laplace校准，即+1（通常取1），当然为了保证概率相等，分母应对应初始化为2（这里因为是2类，所以加2，如果是k类就需要加k，术语上叫做laplace光滑, 分母加k的原因是使之满足全概率公式）。至于+1之后的影响在数据集很大的情况下可以忽略。（即使贝叶斯在小规模数据集表现更好，但相较之下“1”还是微不足道的）

所有特征出现概率都很低？稀疏数据问题。
如果离散的数据很稀疏时，可以假设x符合伯努利分布以便于计算（在scikit-learn中有GaussianNB（高斯分布，适用连续值），MultinomialNB（多项式分布，适用离散值）和BernoulliNB（伯努利分布）三种实现。）。

非离散值怎么办？参数估计问题。
当特征为连续值时，通过极大似然（maximum likelihood，ML）求期望和方差就行了。极大似然正如它的名字，求的就是在该观测下的最可能的参数，不过对多项乘积的求导往往非常复杂，对于多项求和的求导却要简单的多，所以会log。

“朴素”是什么？为什么要“朴素”？达不到朴素怎么办？贝叶斯的变体。
“朴素”是朴素贝叶斯算法的核心，即基于假设特征之间相互独立。设这个前提的目的是为了避免组合爆炸，样本稀疏问题等问题。而在实际中这个假设往往不成立，从而导致分类效果受影响。
改进方法有很多，从特征间的关系来考虑的话，可以对特征进行分组使组内关联而组间独立；删除部分重合或者依赖性强的“冗余”特征；对某些特征加权（APNBC（根据效果会对权重进行二次加权调整），WNB（基于特征重要性）等）；基于互信息的INB，即每个条件属性对属性的重要度采用互信息度量（统计独立关系）。
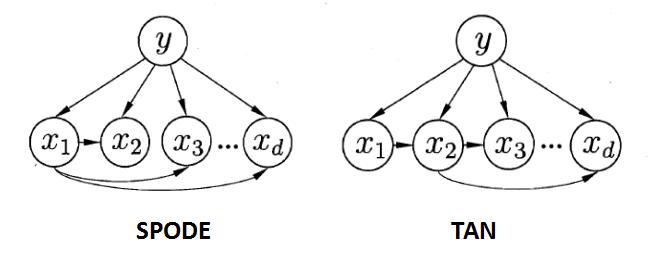
也可以直接降低“朴素”的门槛，产生了半朴素贝叶斯分类器（semi_naive Bayes classifiers，SNBC）。它的基本想法是适当的考虑一部分属性间的相互依赖信息，从而既不完全联合概率计算，又不至于彻底忽略比较强的属性依赖关系，它折中了朴素贝叶斯和贝叶斯网络，限制网络的结构复杂程度，重点在于如何聚集依赖关系较大的属性，其中最直接的方法就是假设所有的属性都归于同一个属性“超父”，然后通过交叉验证来确定超父属性，由此形成了SPODE方法（Super_Parent ODE）。以特征之间的条件互信息作为权值构建完全图，再根据该完全图再构建一个最大带权生成树来挑选的TAN方法（Tree Augmented naive Bayes）, 其中的条件互信息为：$$I(x_i,x_j|y)=\sum _{x_i,x_j;y\in Y}P(x_i,x_j|y)log\frac{P(x_i,x_j|y)}{P(x_i|y)P(x_j|y)}$$最后可以用Boosting和Bagging技术，或者整合其他算法，诸如SVM，遗传算法等来进一步提高性能，比如对每个属性构建SPODE，并将结果集成起来作为最终结果的平均一依赖性评估算法（Averaged One_Dependent Estimator，AODE）。

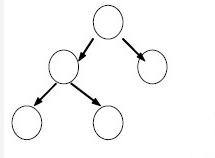
贝叶斯信念网（Bayesian network），它借助有向无环图（Directed Acyclic Graph，DAG）来刻画属性间的依赖关系，并使用条件概率（Conditional Probability Table，CPT）来描述属性的联合概率分布。（其每个结点代表一个随机变量，而每条弧代表一个概率依赖。）

求在贝叶斯信念网中对应于属性集D的任意元组的联合概率将变为:$$P(D_1...D_n)=\prod _{i=1}^{n}P(D_i|parent(D_i)),其中parent是直接前驱$$同样的贝叶斯信念网也存在求解问题，如果贝叶斯信念网是确定的，即网络图结构和概率都已知，那么可以直接进行计算。一旦数据是隐藏的，这时就需要进行条件概率的估算，需要借助梯度下降或EM算法来解决。若它的图结构未知，那么就只能已知数据启发式学习贝叶斯网的结构。K2算法可用于解决此问题。K2算法是贪心算法：先定义一种评价网络结构优劣的评分函数，再从一个包含所有节点、但却没有边的无向图开始，逐个根据事先确定的最大父节点数目和节点次序，选择分值最高的节点作为该节点的父节点。

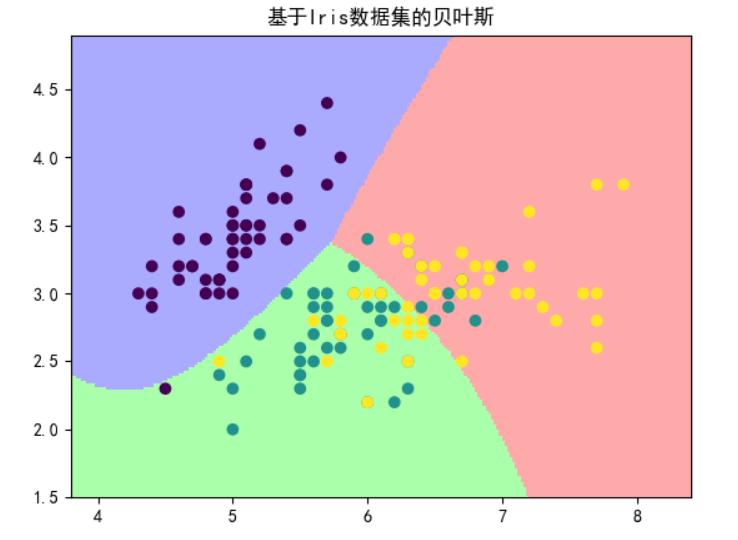
NB应用：
GaussianNB参数说明：
GaussianNB(priors=None)

priors：各类别的先验概率（假设为正态分布）
1

MultinomialNB参数说明：
MultinomialNB(alpha=0.01, class_prior=None, fit_prior=True)

alpha：初始的添加值
class_prior：用户自己输入的先验概率（假设为多项式分布）
fit_prior：是否考虑先验概率
1
2
3

BernoulliNB参数说明：
BernoulliNB(alpha=1.0, binarize=0.0, class_prior=None, fit_prior=True)

alpha：初始的添加值
binarize：用来处理二项分布
class_prior：用户自己输入的先验概率（假设为二元伯努利分布）
fit_prior：是否考虑先验概率
1
2
3
4