一、快速点特征直方图（FPFH）描述子介绍

  对于具有n个点的给定点云P，点特征直方图(PFH)的理论计算复杂度为O($n{k}^2$)，其中k为P中的每个点P的邻点数。但是对于有效率要求或点数量极大的情况，例如稠密点特征计算，PFH的计算复杂度将难以满足要求。有关PFH的内容查看上一篇文章。
  为解决PFH的计算复杂度问题，前辈们将PFH公式进行了简化，形成了快速点特征直方图(FPFH)，它将算法的计算复杂度降低到O(nk)级别，同时仍然保留PFH的大部分能力。

1、快速点特征直方图原理简述
  为了解什么是快速点特征直方图，请务必学习上一篇关于点特征直方图的原理。
再点特征直方图原理的基础上，FPFH对其进行了如下的简化：
  第一步(SPFH)：将每个待计算点$p_q$和其邻近点之间对应的一组元组$⟨$$\alpha$， $\varphi$，$\theta$$⟩$称为简化点特征直方图(SPFH)，与PFH的直接区别是减少了邻近点之间的参数元组，只计算待计算点到其邻近点之间的参数元组。
  第二步(FPFH)：对于每一个点，重新确定它的k个邻居，用相邻点的SPFH对$p_q$的最终直方图进行加权，如下式所示

   其中，权值${\omega }_i$表示在某些给定度量空间中待计算点$p_q$和相邻点$p_i$之间的距离，从而为$(p_q,p_i)$加权，但也可以在必要时选择不同的度量值。为了理解这种加权方案的重要性，下图给出了以$p_q$为中心的k-邻域影响区域图。

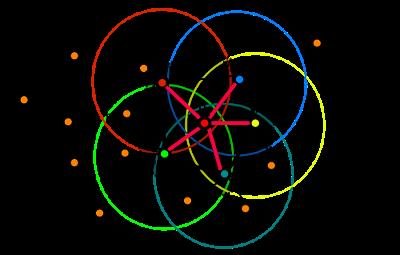
   因此，对于给定的$p_q$，算法首先通过在它自己和它的邻点估计它的SPFH值(用红线表示)。对数据集中的所有点重复这一操作，然后使用它的k个邻居的SPFH值对$p_q$的SPFH值进行重新加权，从而为$p_q$创建FPFH。这种操作会有一些点对的参数元组将被计算两次(在图中用较粗的线标记)
  
  
2、PFH和FPFH的异同

   PFH和FPFH配方之间的主要区别总结如下:

  1.从图中可以看出，FPFH并不完全连接$p_q$的所有邻居，因此缺少一些值对，这可能有助于捕获点周围的几何图形;
  2.PFH模型精确确定待计算点的周围，而FPFH包括超半径球面(最多2r球面)内的其他邻点信息;
  3.由于重新加权的方法，FPFH结合了SPFH值，并重新捕获了一些邻近点;
  4.FPFH的总体复杂度大大降低，从而使其可以在实时应用中使用;
  5.最终的直方图通过解关联这些FPFH值来简化，也就是简单地创建很多个独立的特征直方图，每个特征维度创建一个，然后将它们连接在一起(见下图)。

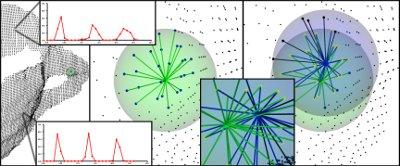
二、示例代码分析

  快速点特征直方图在PCL中作为pcl_features库的一部分。默认的FPFH实现使用11个细分单元(例如，四个特征值中的每一个都会从其值区间中使用这么多的细分单元)，和一个不相关的方案(见上面:特征直方图分别计算后再联接)，这将产生一个33字节的浮点值数组。它们存储在pcl::FPFHSignature33点类型中。下面的代码片段将估计输入数据集中所有点的一组FPFH特性。

#include 
#include 
 
 {
   pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
   pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal> ());
 
	 /*
		 此处通过读取PCD或者创造一组有法向特征的点云。并使上面的指针指向点云，不再赘述
 	*/

 	 // 创建FPFH估计类，并将输入数据集和法线传递给它
  pcl::FPFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh;
  fpfh.setInputCloud (cloud);
  fpfh.setInputNormals (normals);
	// 或者, 如果点云类型是 PointNormal, 使用fpfh.setInputNormals (cloud);

  	// 创建一个空的kdtree表示，并将其传递给PFH对象。
 	// 树的内容将根据给定的输入数据集填充到数对象内部(因为没有给出其他搜索面)。
  pcl::search::KdTree<PointXYZ>::Ptr tree (new pcl::search::KdTree<PointXYZ>);

  fpfh.setSearchMethod (tree);

  // 输出的FPFH描述子
  pcl::PointCloud<pcl::FPFHSignature33>::Ptr fpfhs (new pcl::PointCloud<pcl::FPFHSignature33> ());

  // 使用半径为5cm的球面上的所有邻点
  // 重要:这里使用的半径必须大于用来估计表面法线的半径！！！例如表面法向估计半径为0.02，此处为0.05
  fpfh.setRadiusSearch (0.05);

  // 计算特征
  fpfh.compute (*fpfhs);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

  fpfhestimate类的实际计算调用在其内部只做如下工作：

// 伪代码部分
for each point p in cloud P  //遍历点云中每一个点
	// 步骤一
  1. pass 1:
	// 获取p的最邻近点集
     1. get the nearest neighbors of :math:`p` 
	// 获取p到邻域所有pi的点之间的三个角度值
     2. for each pair of :math:`p, p_i` (where :math:`p_i` is a neighbor of :math:`p`, compute the three angular values
	// 将计算结果装入SPFH直方图
     3. bin all the results in an output SPFH histogram
	// 步骤二
  2. pass 2:
	// 获取p的邻域点
     1. get the nearest neighbors of :math:`p`
	// 使用上一步计算的SPFH作为权重加和得到FPFH
     3. use each SPFH of :math:`p` with a weighting scheme to assemble the FPFH of :math:`p`:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

  拓展：有时我们考虑到效率问题，选择不检查法线是否包含NaN或infinite值。将这些值传递给compute()，但是这将导致未知输出。建议至少在参数设置和程序编写时，增加检查正常值的步骤。这可以通过在调用compute()之前插入以下代码来实现：

for (int i = 0; i < normals->size(); i++)
{
  if (!pcl::isFinite<pcl::Normal>((*normals)[i]))
  {
    PCL_WARN("normals[%d] is not finite\n", i);
  }
}
1
2
3
4
5
6
7

  在代码编写中，应该设置预处理步骤和参数，使法线是有限的否则将引发错误。若需要进一步增加效率可以在多核处理器的计算机内使用OpenMP多线程计算，具体为使用pcl::FPFHEstimationOMP 替代pcl::FPFHEstimation指令，使用方法一致。

总结：
  本篇文章介绍了什么是FPFH点特征直方图及与PFH的区别，并通过示例程序分析了如何使用Feature模块中快速点特征直方图计算的流程。下一篇文章将进一步介绍视点特征直方图(VFH)的原理和使用。

【博主简介】
  斯坦福的兔子，男，95，天津大学机械工程工学硕士。21年毕业至今从事光学三维成像及点云处理相关工作。因工作中使用的三维处理库为公司内部库，不具有普遍适用性，遂自学开源PCL库及其相关数学知识以备使用。谨此将自学过程与君共享。
博主才疏学浅，尚不具有指导能力，如有问题还请各位在评论处留言供大家共同讨论。
若前辈们有工作机会介绍欢迎私信。