前言

数据结构与算法作为计算机科学的基础，是一个重点和难点，在实际编程中似乎看不它们的身影，但是它们有随处不在，如影随形。

本系列博客是《数据结构与算法分析—Java语言描述》的读书笔记，合集文章列表如下：

数据结构与算法（Data Structures and Algorithm）——跟着Mark Allen Weiss用Java语言学习数据结构与算法

本篇博客介绍二叉堆(binary heap)，它的使用对于PriorityQueue（优先队列）的实现相当普遍，以至于当堆(heap)这个词不加修饰地用在优先队列的上下文中时，一般都是指数据结构的这种实现。

其他相关的本书的学习笔记博客文章列表如下：

• Java学数据结构（1）——抽象数据类型ADT & 表List、栈Stack和队列Qeue

• Java学数据结构（2）——树Tree & 二叉树binary tree & 二叉查找树 & AVL树 & 树的遍历

• Java学数据结构（3）——树Tree & B树 & 红黑树 & Java标准库中的集合Set与映射Map & 使用多个映射Map的案例

• Java学数据结构（4）——散列表Hash table & 散列函数 & 哈希冲突

引出

1.PriorityQueue（优先队列）是一种特殊的队列数据结构，其中每个元素都有一个优先级；
2.insert(插入)和deleteMin(删除最小者)的方式；

优先队列（堆）

虽然发送到打印机的作业一般被放到队列中，但这未必总是最好的做法。例如，可能有一项作业特别重要，因此希望只要打印机一有空闲就来处理这项作业。反之，若在打印机有空时正好有多个单页的作业及一项100页的作业等待打印，则更合理的做法也许是最后处理长的作业，尽管它不是最后提交上来的（不幸的是，大多数的系统并不这么做，有时可能特别令人懊恼）。

类似地，在多用户环境中，操作系统调度程序必须决定在若干进程中运行哪个进程。一般一个进程只被允许运行一个固定的时间片。一种算法是使用一个队列。开始时作业被放到队列的末尾。调度程序将反复提取队列中的第一个作业并运行它，直到运行完毕，或者该作业的时间片用完，并在作业未运行完毕时把它放到队列的末尾。

这种策略一般并不太合适，因为一些很短的作业由于一味等待运行而要花费很长的时间去处理。一般说来，短的作业要尽可能快地结束，这一点很重要，因此在已经运行的作业当中这些短作业应该拥有优先权。此外，有些作业虽不短小但很重要，也应该拥有优先权。这种特殊的应用似乎需要一类特殊的队列，我们称之为优先队列(priority queue)。

• 优先队列ADT的有效实现。
• 优先队列的使用。
• 优先队列的高级实现

我们将看到的这类数据结构属于计算机科学中最精致的一种

PriorityQueue（优先队列）是一种特殊的队列数据结构，其中每个元素都有一个优先级。在PriorityQueue中，元素按照优先级的顺序进行排序，具有最高优先级的元素最先被取出。

下面是一些PriorityQueue的应用案例：

1. 任务调度：在一个多任务系统中，每个任务都有不同的优先级。可以使用PriorityQueue来管理任务队列，确保高优先级的任务先被执行。
2. 事件处理：在事件驱动的系统中，事件可能具有不同的优先级。PriorityQueue可以用于按照优先级处理事件，确保高优先级的事件先被处理。
3. 路由算法：在网络路由中，路由器需要根据不同的路由策略选择最佳的路径。PriorityQueue可以用于存储和排序路由信息，以便选择最佳路径。
4. 资源分配：在资源管理系统中，资源可能有不同的优先级和需求。PriorityQueue可以用于按照优先级分配资源，确保高优先级的任务获得足够的资源。
5. 任务调度器：在操作系统中，任务调度器负责管理和调度进程。PriorityQueue可以用于按照进程的优先级进行调度，确保高优先级的进程先被执行。

这些只是PriorityQueue的一些应用案例，实际上，PriorityQueue在许多领域都有广泛的应用，特别是需要按照优先级进行排序和处理的场景。

优先队列是允许至少下列两种操作的数据结构：insert(插入)，它的作用是显而易见的；以及deleteMin(删除最小者)，它的工作是找出、返回并删除优先队列中最小的元素。insert操作等价于enqueue(人队)，而deleteMin则是队列运算dequeue(出队)在优先队列中的等价操作。

二叉堆

我们将要使用的这种工具叫作二叉堆(binary heap),它的使用对于优先队列的实现相当普遍，以至于当堆(heap)这个词不加修饰地用在优先队列的上下文中时，一般都是指数据结构的这种实现。在本节，我们把二叉堆只叫作堆。

像二叉查找树一样，堆也有两个性质，即结构性和堆序性。恰似AVL树，对堆的一次操作可能破坏这两个性质中的一个，因此，堆的操作必须到堆的所有性质都被满足时才能终止。事实上这并不难做到。

结构性质

堆是一棵被完全填满的二叉树，有可能的例外是在底层，底层上的元素从左到右填入。这样的树称为完全二叉树(complete binary tree)。图6-2给出了一个例子

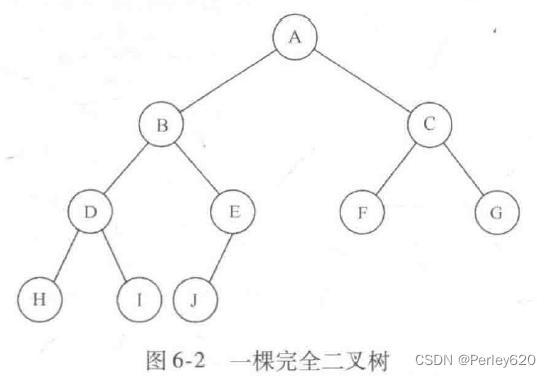
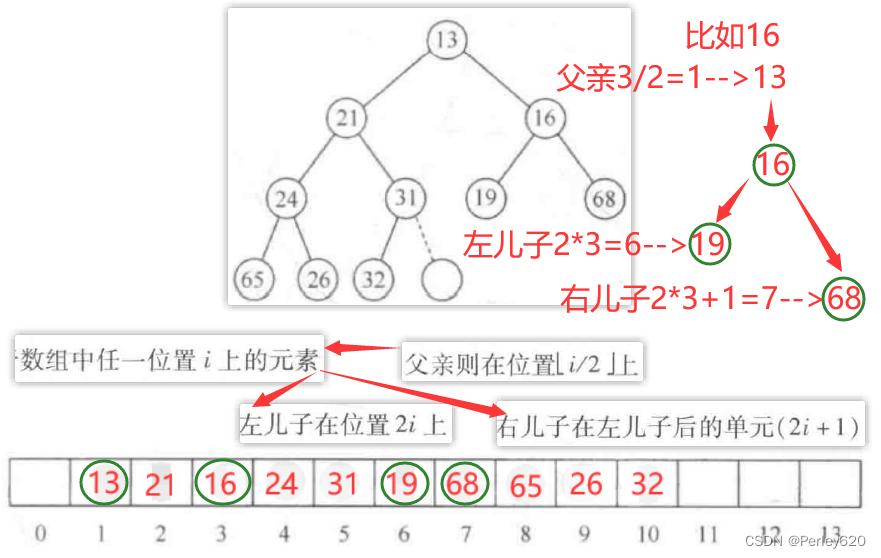
一个重要的观察发现，因为完全二叉树这么有规律，所以它可以用一个数组表示而不需要使用链。图6-3中的数组对应图6-2中的堆。

数据结构的分析

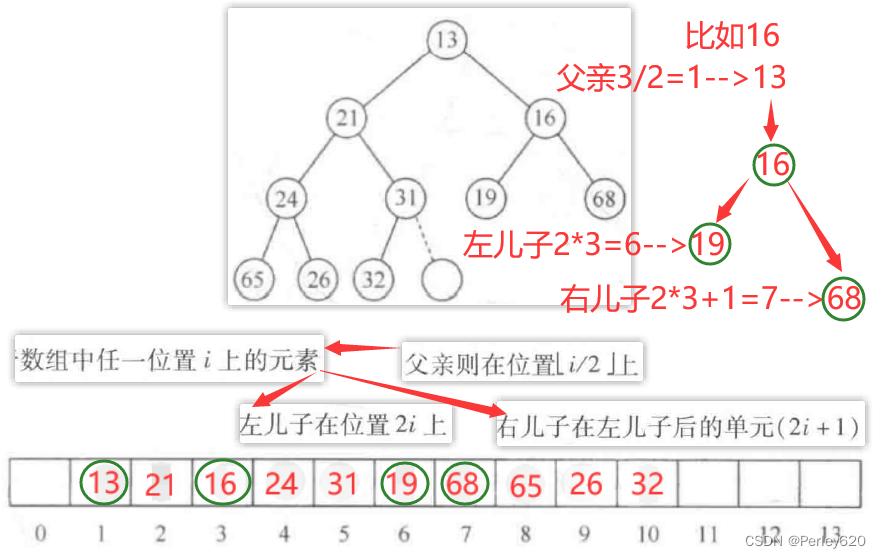
堆序性质

让操作快速执行的性质是堆序性质(heap-order property)。由于我们想要快速找出最小元，因此最小元应该在根上。如果我们考虑任意子树也应该是一个堆，那么任意节点就应该小于它的所有后裔。

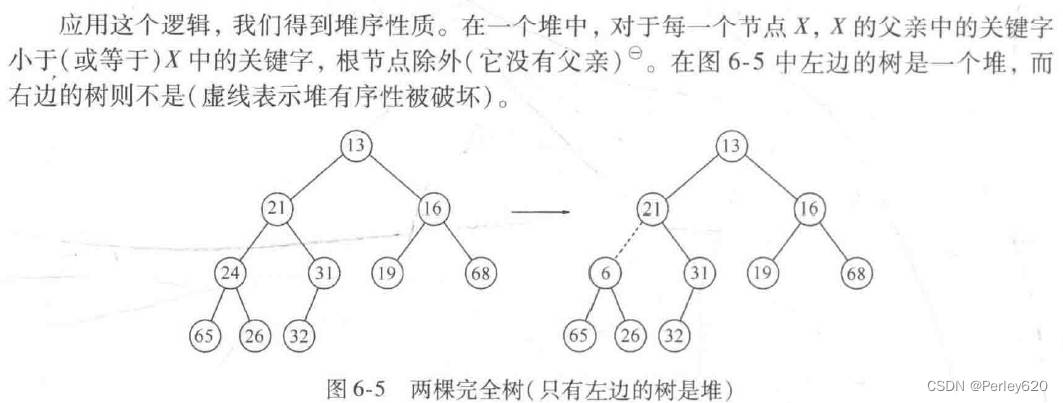
根据堆序性质，最小元总可以在根处找到。因此，我们以常数时间得到附加操作findMin

堆的基本操作

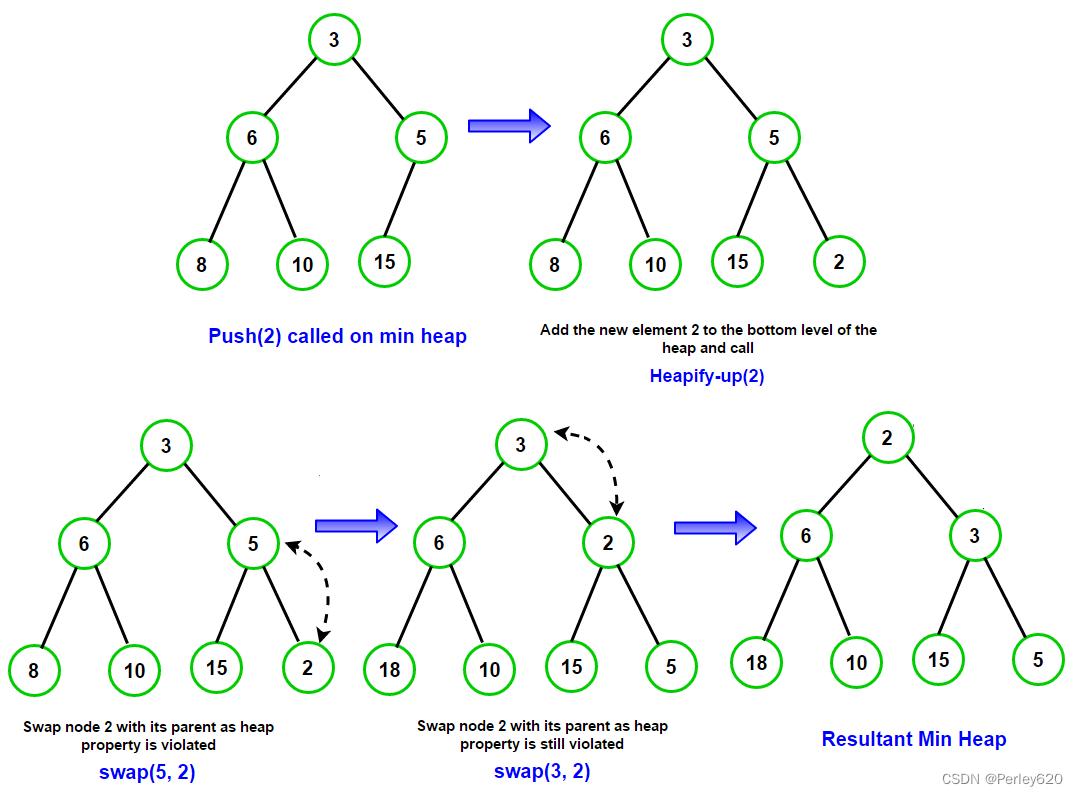
插入元素 (上滤percolate up)

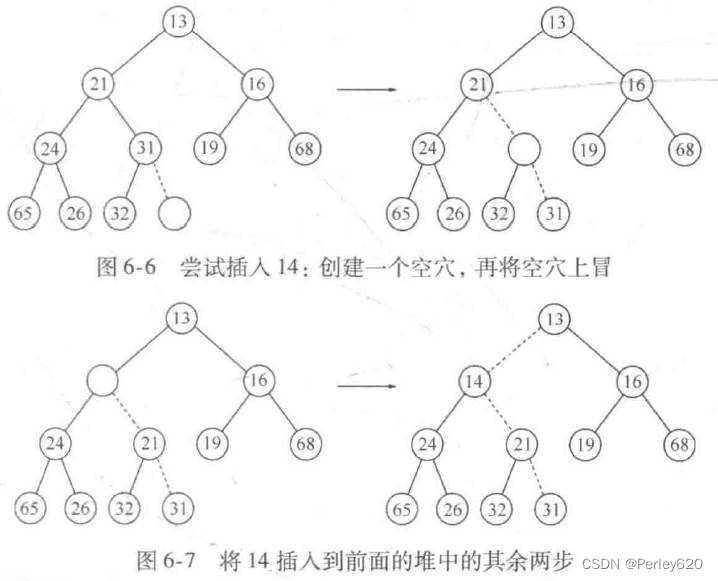
为将一个元素X插入到堆中，我们在下一个可用位置创建一个空穴，否则该堆将不是完全树。如果X可以放在该空穴中而并不破坏堆的序，那么插入完成。否则，我们把空穴的父节点上的元素移人该空穴中，这样，空穴就朝着根的方向上冒一步。继续该过程直到X能被放人空穴中为止。

如图6-6所示，为了插入14，我们在堆的下一个可用位置建立一个空穴。由于将14插入空穴破坏了堆序性质，因此将31移入该空穴。在图6-7中继续这种策略，直到找出置入14的正确位置。

这种一般的策略叫作上滤(percolate up);新元素在堆中上滤直到找出正确的位置。

比如如下的一个堆

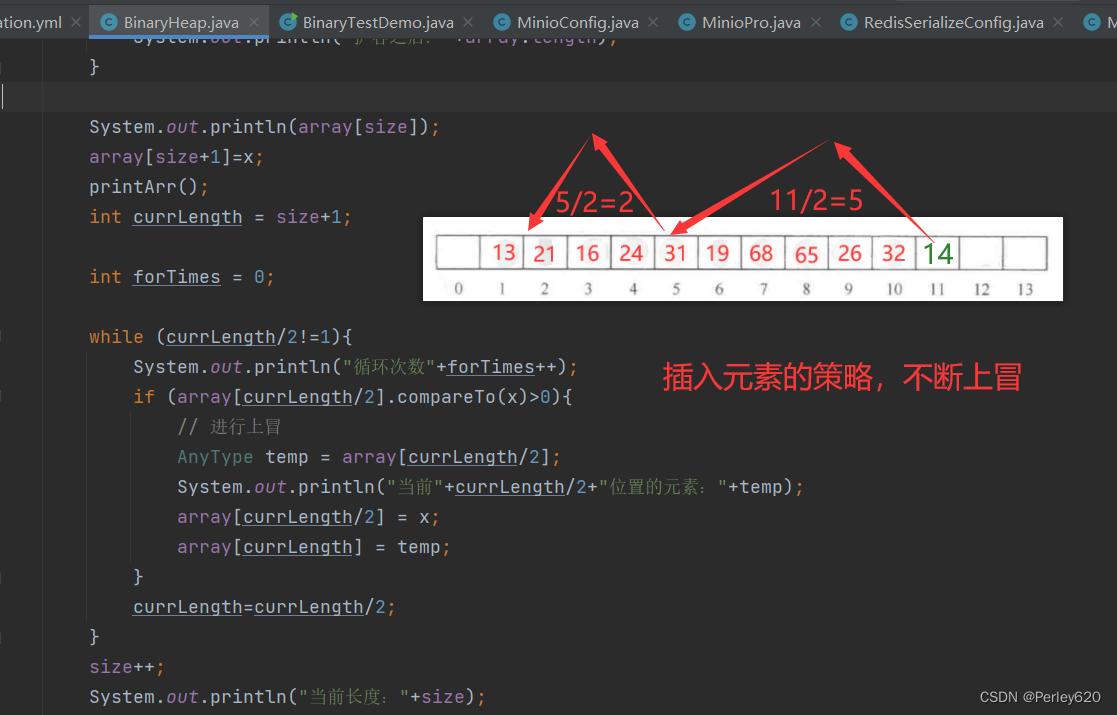
插入元素的流程拆解

全体流程解析

package com.tianju.security.dataStructure.head;


import java.util.Arrays;
import java.util.List;

public class BinaryHeap<AnyType extends Comparable<? super AnyType>> {

    private AnyType[] array;

    private int size; // 数组中的元素数量

    private static final int DEFAULT_CAPACITY =10; // 默认容量为10

    public BinaryHeap() {
    }

    public BinaryHeap(AnyType[] array) {
        this.array = array;
        this.size = array.length-1;
    }

    public Integer size(){
        return size;
    }

    public void insert(AnyType x){

        System.out.println("扩容之前："+size);

        // 如果放不下，就扩容
        if (array.length+1>array.length){
            int newLen = array.length + (array.length>>1);
            array = Arrays.copyOf(array, newLen);
            System.out.println("扩容之后："+array.length);
        }

        System.out.println(array[size]);
        array[size+1]=x;
        printArr();
        int currLength = size+1;

        int forTimes = 0;

        while (currLength/2!=1){
            System.out.println("循环次数"+forTimes++);
            if (array[currLength/2].compareTo(x)>0){
                // 进行上冒
                AnyType temp = array[currLength/2];
                System.out.println("当前"+currLength/2+"位置的元素："+temp);
                array[currLength/2] = x;
                array[currLength] = temp;
            }
            currLength=currLength/2;
        }
        size++;
        System.out.println("当前长度："+size);



    }

    public void printArr(){
        System.out.println();
        System.out.print("[");
        StringBuilder s = new StringBuilder("[");
        for(AnyType x:array){
//            System.out.print(x+", ");
            s.append(x).append(", ");
        }
        for (int i=1;i<size;i++){
            System.out.print(array[i]+", ");
        }
        System.out.print("]");
        System.out.println();
        s.append("]");
        System.out.println(s);
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

package com.tianju.security.dataStructure.head;

import java.util.Arrays;
import java.util.List;

public class BinaryTestDemo {
    public static void main(String[] args) {
        List<Integer> list = Arrays.asList(0,13,21,16,24,31,19,68,65,26,32);
        Integer[] array = list.toArray(new Integer[list.size()]);
        BinaryHeap<Integer> binaryHeap = new BinaryHeap<>(array);
        binaryHeap.printArr();

        binaryHeap.insert(14);

        binaryHeap.printArr();
        System.out.println(binaryHeap.size());
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

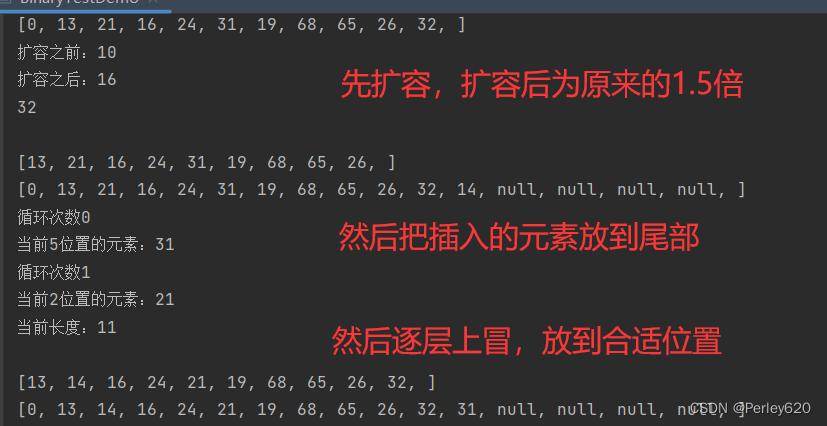
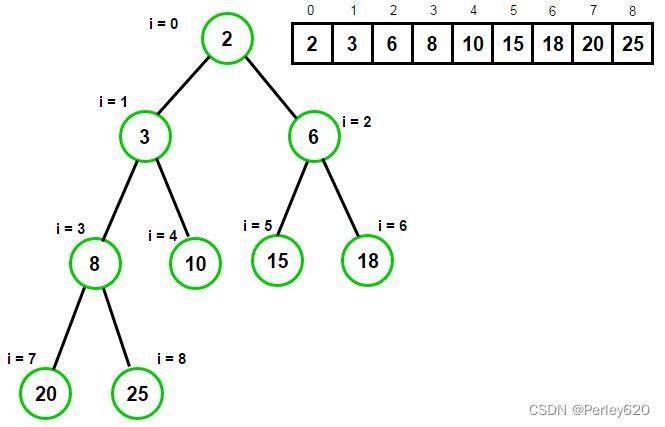
上图的Heap堆插入元素2的流程

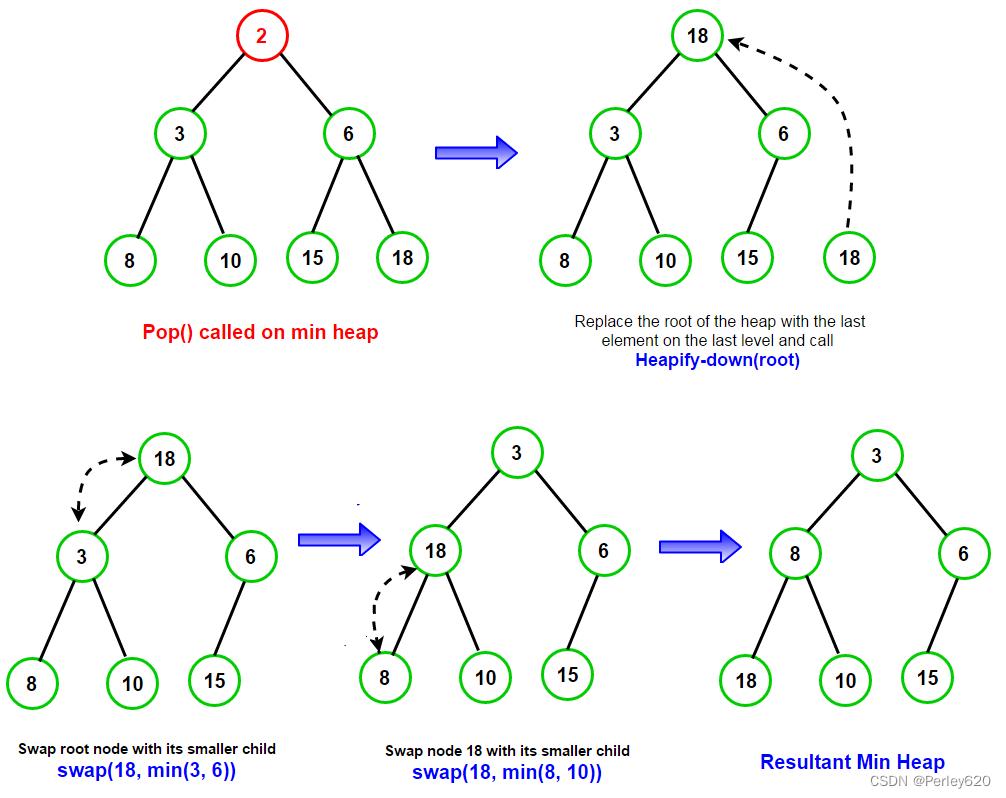
删除最小元素

deleteMin以类似于插入的方式处理。找出最小元是容易的，困难之处是删除它。当删除一个最小元时，要在根节点建立一个空穴。由于现在堆少了一个元素，因此堆中最后一个元素X必须移动到该堆的某个地方。如果X可以被放到空穴中，那么deleteMin完成。不过这一般不太可能，因此我们将空穴的两个儿子中较小者移入空穴，这样就把空穴向下推了一层。重复该步骤直到X可以被放入空穴中。因此，我们的做法是将X置入沿着从根开始包含最小儿子的一条路径上的一个正确的位置。

总结

1.PriorityQueue（优先队列）是一种特殊的队列数据结构，其中每个元素都有一个优先级；
2.insert(插入)和deleteMin(删除最小者)的方式；