NNDL 作业13 优化算法3D可视化

目录

1. 函数3D可视化

（1）x[0]^2+x[1]^2+x[1]^3+x[0]*x[1] ​编辑

（2） x^2 /20+y^2 ​编辑

△△pycharm跑出的3d图像没法旋转怎么办？

2.加入优化算法，画出轨迹

（1）x[0]^2+x[1]^2+x[1]^3+x[0]*x[1] ​编辑

（2） x^2 /20+y^2 ​编辑 

· 结合3D动画，用自己的语言，从轨迹、速度等多个角度讲解各个算法优缺点

​编辑​编辑

3.复现CS231经典动画

·心得总结

1. 函数3D可视化

（1）x[0]^2+x[1]^2+x[1]^3+x[0]*x[1] x[0]^{2}+x[1]^{2}+x[1]^{3}+x[0]*x[1]

代码如下：

  1. import torch
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4.  
  5. class Op(object):
  6.     def __init__(self):
  7.         pass
  8.  
  9.     def __call__(self, inputs):
  10.         return self.forward(inputs)
  11.  
  12.     # 输入：张量inputs
  13.     # 输出：张量outputs
  14.     def forward(self, inputs):
  15.         # return outputs
  16.         raise NotImplementedError
  17.  
  18.     # 输入：最终输出对outputs的梯度outputs_grads
  19.     # 输出：最终输出对inputs的梯度inputs_grads
  20.     def backward(self, outputs_grads):
  21.         # return inputs_grads
  22.         raise NotImplementedError
  23.  
  24.  
  25. class OptimizedFunction3D(Op):
  26.     def __init__(self):
  27.         super(OptimizedFunction3D, self).__init__()
  28.         self.params = {'x': 0}
  29.         self.grads = {'x': 0}
  30.  
  31.     def forward(self, x):
  32.         self.params['x'] = x
  33.         return x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]
  34.  
  35.     def backward(self):
  36.         x = self.params['x']
  37.         gradient1 = 2 * x[0] + x[1]
  38.         gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]
  39.         grad1 = torch.Tensor([gradient1])
  40.         grad2 = torch.Tensor([gradient2])
  41.         self.grads['x'] = torch.cat([grad1, grad2])
  42.  
  43.  
  44. x1 = np.arange(-3, 3, 0.1)
  45. x2 = np.arange(-3, 3, 0.1)
  46. x1, x2 = np.meshgrid(x1, x2)
  47. init_x = torch.Tensor(np.array([x1, x2]))
  48.  
  49. model = OptimizedFunction3D()
  50.  
  51. # 绘制 f_3d函数 的 三维图像
  52. fig = plt.figure()
  53. ax = plt.axes(projection='3d')
  54.  
  55. X = init_x[0].numpy()
  56. Y = init_x[1].numpy()
  57. Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
  58. ax.plot_surface(X, Y, Z, cmap='rainbow')
  59.  
  60. ax.set_xlabel('x1')
  61. ax.set_ylabel('x2')
  62. ax.set_zlabel('f(x1,x2)')
  63. plt.show()

图像展示：

图像特征分析：

 从函数上分析， x[0]^{2}+x[1]^{2}+x[1]^{3}+x[0]*x[1] 这个函数中有二次项、三次项、交叉项。二次项和三次项构成高低起伏的曲面，而交叉项使函数图像呈现出非线性特征。因此这个图像应该是高低不平、起伏没有规律的曲面。

由图像可以看出（颜色），该图像整体呈向下趋势，但中间偏蓝色，向下凹去——这就是“局部最小值”。而纵观整体，可以看出向下有更低的位置，也就是还有全局最小值的存在。因此中间的点可以称为“鞍点”。

什么是鞍点？

（2） x^2 /20+y^2 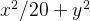x^{2} /20+y^{2}

代码实现：

  1. import torch
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4.  
  5.  
  6. class Op(object):
  7.     def __init__(self):
  8.         pass
  9.  
  10.     def __call__(self, inputs):
  11.         return self.forward(inputs)
  12.  
  13.     # 输入：张量inputs
  14.     # 输出：张量outputs
  15.     def forward(self, inputs):
  16.         # return outputs
  17.         raise NotImplementedError
  18.  
  19.     # 输入：最终输出对outputs的梯度outputs_grads
  20.     # 输出：最终输出对inputs的梯度inputs_grads
  21.     def backward(self, outputs_grads):
  22.         # return inputs_grads
  23.         raise NotImplementedError
  24.  
  25.  
  26. class OptimizedFunction3D(Op):
  27.     def __init__(self):
  28.         super(OptimizedFunction3D, self).__init__()
  29.         self.params = {'x': 0}
  30.         self.grads = {'x': 0}
  31.  
  32.     def forward(self, x):
  33.         self.params['x'] = x
  34.         return x[0] ** 2 / 20 + x[1] ** 2
  35.  
  36.     def backward(self):
  37.         x = self.params['x']
  38.         gradient1 = 2 * x[0] + x[1]
  39.         gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]
  40.         grad1 = torch.Tensor([gradient1])
  41.         grad2 = torch.Tensor([gradient2])
  42.         self.grads['x'] = torch.cat([grad1, grad2])
  43.  
  44.  
  45. x1 = np.arange(-40, 40, 0.1)
  46. x2 = np.arange(-40, 40, 0.1)
  47. x1, x2 = np.meshgrid(x1, x2)
  48. init_x = torch.Tensor(np.array([x1, x2]))
  49.  
  50. model = OptimizedFunction3D()
  51.  
  52. # 绘制 f_3d函数 的 三维图像
  53. fig = plt.figure()
  54. ax = plt.axes(projection='3d')
  55.  
  56. X = init_x[0].numpy()
  57. Y = init_x[1].numpy()
  58. Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
  59. ax.plot_surface(X, Y, Z, cmap='rainbow')
  60.  
  61. ax.set_xlabel('x1')
  62. ax.set_ylabel('x2')
  63. ax.set_zlabel('f(x1,x2)')
  64. plt.show()

图像实现：

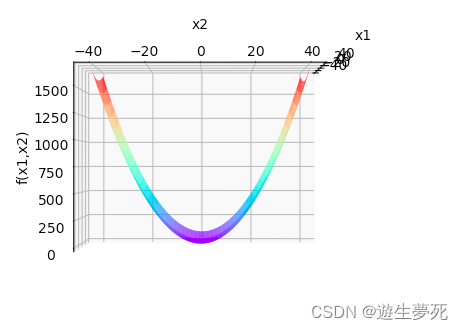
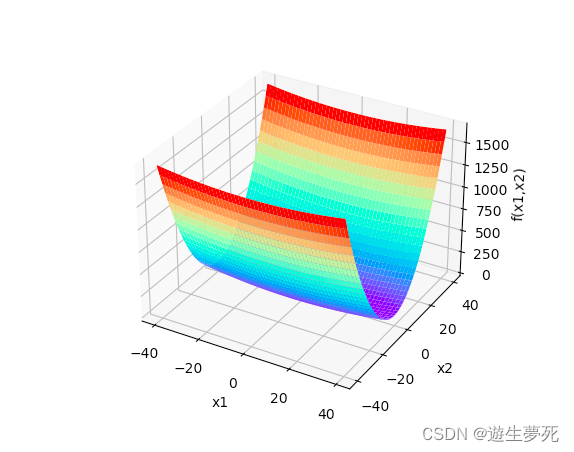
图像分析：这个图像上课老师已经分析过了，就不多说了。这个函数乍一看和上一次作业（NNDL 作业12 优化算法2D可视化-CSDN博客）分析过的x2" role="presentation" style="position: relative;">x2有点像,但后者是二次函数，是一个二维模型就可以表示的，但这个函数只有中间是最低点，从上图可以看出，该函数的模型中间也有一个弧度，该点才是全局最小值。

△△pycharm跑出的3d图像没法旋转怎么办？

这个问题能不能解决还得看搜索引擎给不给力，第一次查这个问题一知半解的，搜索引擎直接把我送到svn那儿去了，整得我又是安装homebrew又是安装svn，中间还泡了一碗面。最后才知道原来在设置里改一下就行……

新版pycharm ui可以去偏好设置里直接找“偏好设置 | 工具 | Python Scientific”->“在工具窗口显示绘图”，然后把对勾去掉就行。

说实话眼神不好的话真的挺难找……因为我在查找里一直搜的是“科学模式”，也没搜到这个指路，所以就怀疑工具里是不是没有“python scientific”，还特地换成了经典ui去找这个功能。

好在大概是我的晕头转向坚持不懈感动了上天，第n次打开偏好模式，走神的时候随手一点居然就是python scientific，总算是解决了这个问题。

2.加入优化算法，画出轨迹

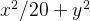分别画出x[0]^{2}+x[1]^{2}+x[1]^{3}+x[0]*x[1] 和 x^{2} /20+y^{2}的3D轨迹图

（1）x[0]^2+x[1]^2+x[1]^3+x[0]*x[1] x[0]^{2}+x[1]^{2}+x[1]^{3}+x[0]*x[1]

代码如下：

  1. import torch
  2. import numpy as np
  3. import copy
  4. from matplotlib import pyplot as plt
  5. from matplotlib import animation
  6. from itertools import zip_longest
  7.  
  8.  
  9. class Op(object):
  10.     def __init__(self):
  11.         pass
  12.  
  13.     def __call__(self, inputs):
  14.         return self.forward(inputs)
  15.  
  16.     # 输入：张量inputs
  17.     # 输出：张量outputs
  18.     def forward(self, inputs):
  19.         # return outputs
  20.         raise NotImplementedError
  21.  
  22.     # 输入：最终输出对outputs的梯度outputs_grads
  23.     # 输出：最终输出对inputs的梯度inputs_grads
  24.     def backward(self, outputs_grads):
  25.         # return inputs_grads
  26.         raise NotImplementedError
  27.  
  28.  
  29. class Optimizer(object):  # 优化器基类
  30.     def __init__(self, init_lr, model):
  31.         """
  32.         优化器类初始化
  33.         """
  34.         # 初始化学习率，用于参数更新的计算
  35.         self.init_lr = init_lr
  36.         # 指定优化器需要优化的模型
  37.         self.model = model
  38.  
  39.     def step(self):
  40.         """
  41.         定义每次迭代如何更新参数
  42.         """
  43.         pass
  44.  
  45.  
  46. class SimpleBatchGD(Optimizer):
  47.     def __init__(self, init_lr, model):
  48.         super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
  49.  
  50.     def step(self):
  51.         # 参数更新
  52.         if isinstance(self.model.params, dict):
  53.             for key in self.model.params.keys():
  54.                 self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]
  55.  
  56.  
  57. class Adagrad(Optimizer):
  58.     def __init__(self, init_lr, model, epsilon):
  59.         """
  60.         Adagrad 优化器初始化
  61.         输入：
  62.             - init_lr： 初始学习率 - model：模型，model.params存储模型参数值  - epsilon：保持数值稳定性而设置的非常小的常数
  63.         """
  64.         super(Adagrad, self).__init__(init_lr=init_lr, model=model)
  65.         self.G = {}
  66.         for key in self.model.params.keys():
  67.             self.G[key] = 0
  68.         self.epsilon = epsilon
  69.  
  70.     def adagrad(self, x, gradient_x, G, init_lr):
  71.         """
  72.         adagrad算法更新参数，G为参数梯度平方的累计值。
  73.         """
  74.         G += gradient_x ** 2
  75.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  76.         return x, G
  77.  
  78.     def step(self):
  79.         """
  80.         参数更新
  81.         """
  82.         for key in self.model.params.keys():
  83.             self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
  84.                                                                self.model.grads[key],
  85.                                                                self.G[key],
  86.                                                                self.init_lr)
  87.  
  88.  
  89. class RMSprop(Optimizer):
  90.     def __init__(self, init_lr, model, beta, epsilon):
  91.         """
  92.         RMSprop优化器初始化
  93.         输入：
  94.             - init_lr：初始学习率
  95.             - model：模型，model.params存储模型参数值
  96.             - beta：衰减率
  97.             - epsilon：保持数值稳定性而设置的常数
  98.         """
  99.         super(RMSprop, self).__init__(init_lr=init_lr, model=model)
  100.         self.G = {}
  101.         for key in self.model.params.keys():
  102.             self.G[key] = 0
  103.         self.beta = beta
  104.         self.epsilon = epsilon
  105.  
  106.     def rmsprop(self, x, gradient_x, G, init_lr):
  107.         """
  108.         rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
  109.         """
  110.         G = self.beta * G + (1 - self.beta) * gradient_x ** 2
  111.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  112.         return x, G
  113.  
  114.     def step(self):
  115.         """参数更新"""
  116.         for key in self.model.params.keys():
  117.             self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
  118.                                                                self.model.grads[key],
  119.                                                                self.G[key],
  120.                                                                self.init_lr)
  121.  
  122.  
  123. class Momentum(Optimizer):
  124.     def __init__(self, init_lr, model, rho):
  125.         """
  126.         Momentum优化器初始化
  127.         输入：
  128.             - init_lr：初始学习率
  129.             - model：模型，model.params存储模型参数值
  130.             - rho：动量因子
  131.         """
  132.         super(Momentum, self).__init__(init_lr=init_lr, model=model)
  133.         self.delta_x = {}
  134.         for key in self.model.params.keys():
  135.             self.delta_x[key] = 0
  136.         self.rho = rho
  137.  
  138.     def momentum(self, x, gradient_x, delta_x, init_lr):
  139.         """
  140.         momentum算法更新参数，delta_x为梯度的加权移动平均
  141.         """
  142.         delta_x = self.rho * delta_x - init_lr * gradient_x
  143.         x += delta_x
  144.         return x, delta_x
  145.  
  146.     def step(self):
  147.         """参数更新"""
  148.         for key in self.model.params.keys():
  149.             self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
  150.                                                                       self.model.grads[key],
  151.                                                                       self.delta_x[key],
  152.                                                                       self.init_lr)
  153.  
  154.  
  155. class Nesterov(Optimizer):
  156.     def __init__(self, init_lr, model, rho):
  157.         super(Nesterov, self).__init__(init_lr=init_lr, model=model)
  158.         self.delta_x = {}
  159.         for key in self.model.params.keys():
  160.             self.delta_x[key] = 0
  161.         self.rho = rho
  162.  
  163.     def nesterov(self, x, gradient_x, delta_x, init_lr):
  164.         """
  165.         Nesterov算法更新参数，delta_x为梯度的加权移动平均
  166.         """
  167.         delta_x_prev = delta_x
  168.         delta_x = self.rho * delta_x - init_lr * gradient_x
  169.         x += -self.rho * delta_x_prev + (1 + self.rho) * delta_x
  170.         return x, delta_x
  171.  
  172.     def step(self):
  173.         """参数更新"""
  174.         for key in self.model.params.keys():
  175.             self.model.params[key], self.delta_x[key] = self.nesterov(self.model.params[key],
  176.                                                                       self.model.grads[key],
  177.                                                                       self.delta_x[key],
  178.                                                                       self.init_lr)
  179.  
  180.  
  181. class Adam(Optimizer):
  182.     def __init__(self, init_lr, model, beta1, beta2, epsilon):
  183.         """
  184.         Adam优化器初始化
  185.         输入：
  186.             - init_lr：初始学习率
  187.             - model：模型，model.params存储模型参数值
  188.             - beta1, beta2：移动平均的衰减率
  189.             - epsilon：保持数值稳定性而设置的常数
  190.         """
  191.         super(Adam, self).__init__(init_lr=init_lr, model=model)
  192.         self.beta1 = beta1
  193.         self.beta2 = beta2
  194.         self.epsilon = epsilon
  195.         self.M, self.G = {}, {}
  196.         for key in self.model.params.keys():
  197.             self.M[key] = 0
  198.             self.G[key] = 0
  199.         self.t = 1
  200.  
  201.     def adam(self, x, gradient_x, G, M, t, init_lr):
  202.         """
  203.         adam算法更新参数
  204.         输入：
  205.             - x：参数
  206.             - G：梯度平方的加权移动平均
  207.             - M：梯度的加权移动平均
  208.             - t：迭代次数
  209.             - init_lr：初始学习率
  210.         """
  211.         M = self.beta1 * M + (1 - self.beta1) * gradient_x
  212.         G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
  213.         M_hat = M / (1 - self.beta1 ** t)
  214.         G_hat = G / (1 - self.beta2 ** t)
  215.         t += 1
  216.         x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
  217.         return x, G, M, t
  218.  
  219.     def step(self):
  220.         """参数更新"""
  221.         for key in self.model.params.keys():
  222.             self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
  223.                                                                                  self.model.grads[key],
  224.                                                                                  self.G[key],
  225.                                                                                  self.M[key],
  226.                                                                                  self.t,
  227.                                                                                  self.init_lr)
  228.  
  229.  
  230. class OptimizedFunction3D(Op):
  231.     def __init__(self):
  232.         super(OptimizedFunction3D, self).__init__()
  233.         self.params = {'x': 0}
  234.         self.grads = {'x': 0}
  235.  
  236.     def forward(self, x):
  237.         self.params['x'] = x
  238.         return x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]
  239.  
  240.     def backward(self):
  241.         x = self.params['x']
  242.         gradient1 = 2 * x[0] + x[1]
  243.         gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]
  244.         grad1 = torch.Tensor([gradient1])
  245.         grad2 = torch.Tensor([gradient2])
  246.         self.grads['x'] = torch.cat([grad1, grad2])
  247.  
  248.  
  249. class Visualization3D(animation.FuncAnimation):
  250.     """    绘制动态图像，可视化参数更新轨迹    """
  251.  
  252.     def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=600, blit=True, **kwargs):
  253.         """
  254.         初始化3d可视化类
  255.         输入：
  256.             xy_values：三维中x,y维度的值
  257.             z_values：三维中z维度的值
  258.             labels：每个参数更新轨迹的标签
  259.             colors：每个轨迹的颜色
  260.             interval：帧之间的延迟（以毫秒为单位）
  261.             blit：是否优化绘图
  262.         """
  263.         self.fig = fig
  264.         self.ax = ax
  265.         self.xy_values = xy_values
  266.         self.z_values = z_values
  267.  
  268.         frames = max(xy_value.shape[0] for xy_value in xy_values)
  269.         self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]
  270.                       for _, label, color in zip_longest(xy_values, labels, colors)]
  271.         super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,
  272.                                               interval=interval, blit=blit, **kwargs)
  273.  
  274.     def init_animation(self):
  275.         # 数值初始化
  276.         for line in self.lines:
  277.             line.set_data([], [])
  278.             line.set_3d_properties(np.asarray([]))  # 源程序中有这一行，加上会报错。 Edit by David 2022.12.4
  279.         return self.lines
  280.  
  281.     def animate(self, i):
  282.         # 将x,y,z三个数据传入，绘制三维图像
  283.         for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):
  284.             line.set_data(xy_value[:i, 0], xy_value[:i, 1])
  285.             line.set_3d_properties(z_value[:i])
  286.         return self.lines
  287.  
  288.  
  289. def train_f(model, optimizer, x_init, epoch):
  290.     x = x_init
  291.     all_x = []
  292.     losses = []
  293.     for i in range(epoch):
  294.         all_x.append(copy.deepcopy(x.numpy()))  # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.
  295.         loss = model(x)
  296.         losses.append(loss)
  297.         model.backward()
  298.         optimizer.step()
  299.         x = model.params['x']
  300.     return torch.Tensor(np.array(all_x)), losses
  301.  
  302.  
  303. # 构建5个模型，分别配备不同的优化器
  304. model1 = OptimizedFunction3D()
  305. opt_gd = SimpleBatchGD(init_lr=0.01, model=model1)
  306.  
  307. model2 = OptimizedFunction3D()
  308. opt_adagrad = Adagrad(init_lr=0.5, model=model2, epsilon=1e-7)
  309.  
  310. model3 = OptimizedFunction3D()
  311. opt_rmsprop = RMSprop(init_lr=0.1, model=model3, beta=0.9, epsilon=1e-7)
  312.  
  313. model4 = OptimizedFunction3D()
  314. opt_momentum = Momentum(init_lr=0.01, model=model4, rho=0.9)
  315.  
  316. model5 = OptimizedFunction3D()
  317. opt_adam = Adam(init_lr=0.1, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
  318.  
  319. model6 = OptimizedFunction3D()
  320. opt_nesterov = Nesterov(init_lr=0.01, model=model6, rho=0.9)
  321.  
  322. models = [model1, model2, model3, model4, model5, model6]
  323. opts = [opt_gd, opt_adagrad, opt_rmsprop, opt_momentum, opt_adam, opt_nesterov]
  324.  
  325. x_all_opts = []
  326. z_all_opts = []
  327.  
  328. # 使用不同优化器训练
  329.  
  330. for model, opt in zip(models, opts):
  331.     x_init = torch.FloatTensor([2, 3])
  332.     x_one_opt, z_one_opt = train_f(model, opt, x_init, 150)  # epoch
  333.     # 保存参数值
  334.     x_all_opts.append(x_one_opt.numpy())
  335.     z_all_opts.append(np.squeeze(z_one_opt))
  336.  
  337. # 使用numpy.meshgrid生成x1,x2矩阵，矩阵的每一行为[-3, 3]，以0.1为间隔的数值
  338. x1 = np.arange(-3, 3, 0.1)
  339. x2 = np.arange(-3, 3, 0.1)
  340. x1, x2 = np.meshgrid(x1, x2)
  341. init_x = torch.Tensor(np.array([x1, x2]))
  342.  
  343. model = OptimizedFunction3D()
  344.  
  345. # 绘制 f_3d函数 的 三维图像
  346. fig = plt.figure()
  347. ax = plt.axes(projection='3d')
  348.  
  349. X = init_x[0].numpy()
  350. Y = init_x[1].numpy()
  351. Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
  352. ax.plot_surface(X, Y, Z, cmap='rainbow')
  353.  
  354. ax.set_xlabel('x1')
  355. ax.set_ylabel('x2')
  356. ax.set_zlabel('f(x1,x2)')
  357. # 设置观察角度，固定在曲面上方
  358. ax.view_init(elev=30, azim=-60)  # 调整这里的参数可以更改视角
  359.  
  360. labels = ['SGD', 'AdaGrad', 'RMSprop', 'Momentum', 'Adam', 'Nesterov']
  361. colors = ['#3b818c', '#f6f237', '#45f637', '#fed71a', '#815c94', '#f97d1c']
  362.  
  363. animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)
  364.  
  365. ax.legend(loc='upper left')
  366. plt.show()

图像如下：

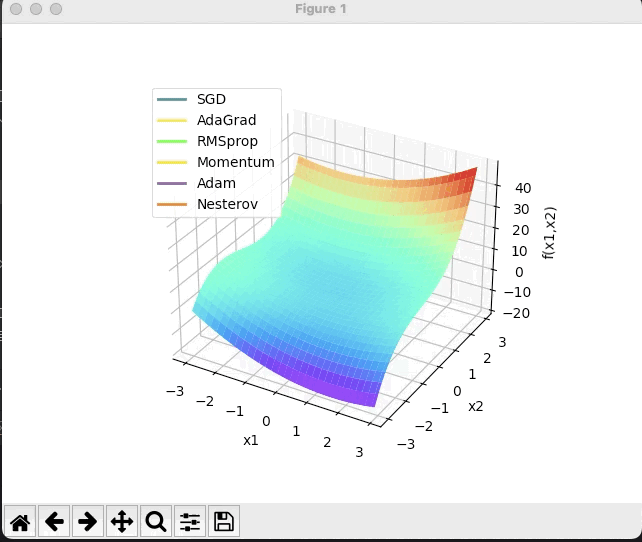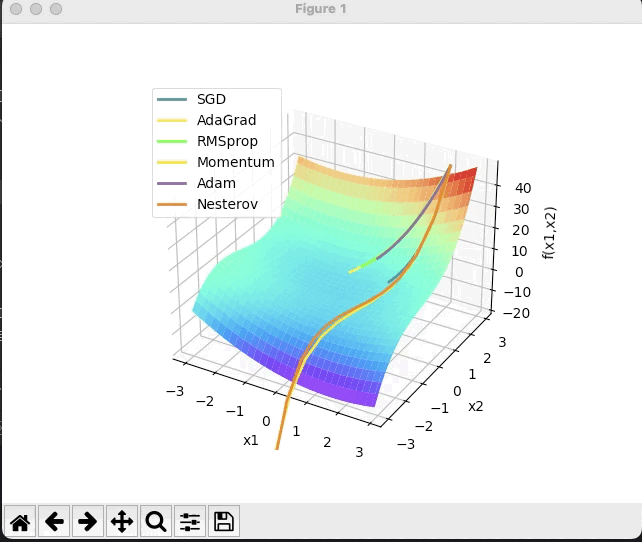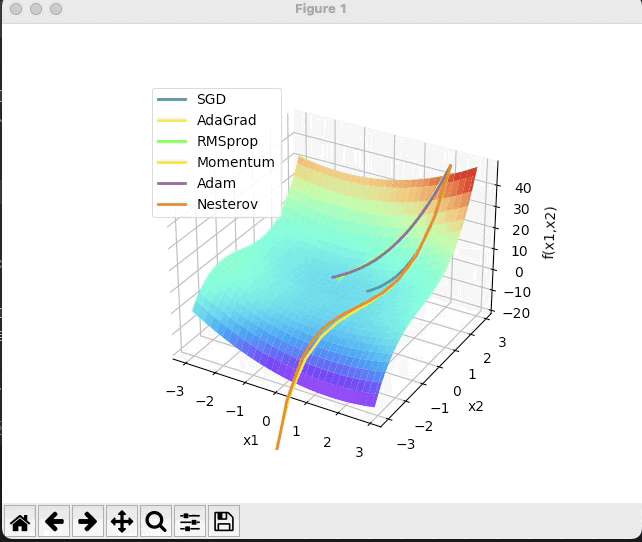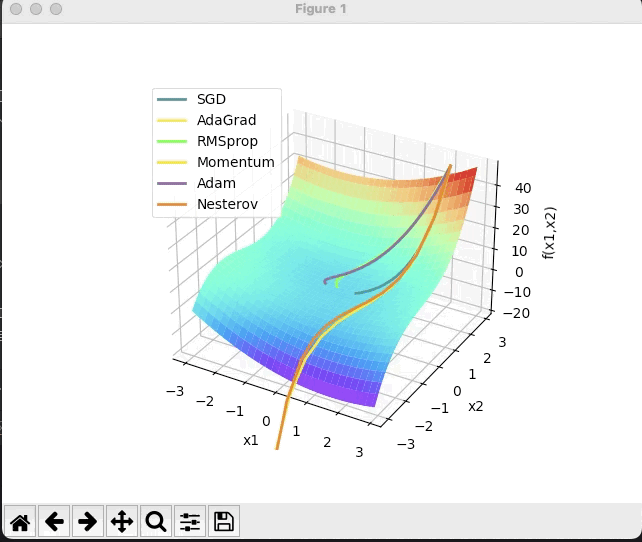
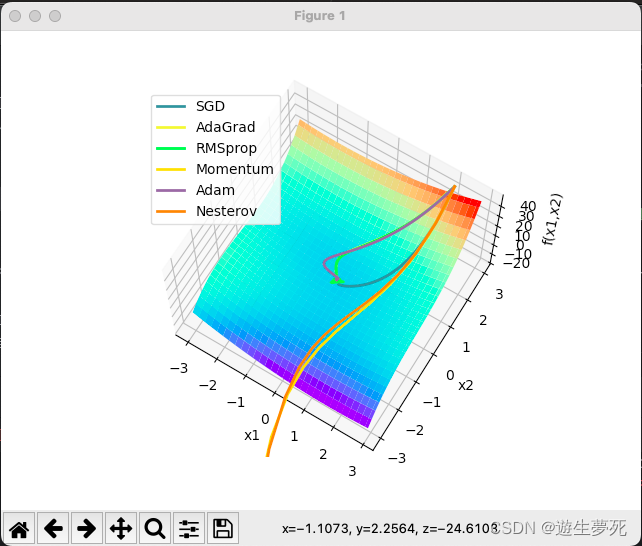
（2） x^2 /20+y^2 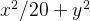x^{2} /20+y^{2} 

代码如下：

  1. import torch
  2. import numpy as np
  3. import copy
  4. from matplotlib import pyplot as plt
  5. from matplotlib import animation
  6. from itertools import zip_longest
  7. from matplotlib import cm
  8.  
  9.  
  10. class Op(object):
  11.     def __init__(self):
  12.         pass
  13.  
  14.     def __call__(self, inputs):
  15.         return self.forward(inputs)
  16.  
  17.     # 输入：张量inputs
  18.     # 输出：张量outputs
  19.     def forward(self, inputs):
  20.         # return outputs
  21.         raise NotImplementedError
  22.  
  23.     # 输入：最终输出对outputs的梯度outputs_grads
  24.     # 输出：最终输出对inputs的梯度inputs_grads
  25.     def backward(self, outputs_grads):
  26.         # return inputs_grads
  27.         raise NotImplementedError
  28.  
  29.  
  30. class Optimizer(object):  # 优化器基类
  31.     def __init__(self, init_lr, model):
  32.         """
  33.         优化器类初始化
  34.         """
  35.         # 初始化学习率，用于参数更新的计算
  36.         self.init_lr = init_lr
  37.         # 指定优化器需要优化的模型
  38.         self.model = model
  39.  
  40.     def step(self):
  41.         """
  42.         定义每次迭代如何更新参数
  43.         """
  44.         pass
  45.  
  46.  
  47. class SimpleBatchGD(Optimizer):
  48.     def __init__(self, init_lr, model):
  49.         super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
  50.  
  51.     def step(self):
  52.         # 参数更新
  53.         if isinstance(self.model.params, dict):
  54.             for key in self.model.params.keys():
  55.                 self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]
  56.  
  57.  
  58. class Adagrad(Optimizer):
  59.     def __init__(self, init_lr, model, epsilon):
  60.         """
  61.         Adagrad 优化器初始化
  62.         输入：
  63.             - init_lr： 初始学习率 - model：模型，model.params存储模型参数值  - epsilon：保持数值稳定性而设置的非常小的常数
  64.         """
  65.         super(Adagrad, self).__init__(init_lr=init_lr, model=model)
  66.         self.G = {}
  67.         for key in self.model.params.keys():
  68.             self.G[key] = 0
  69.         self.epsilon = epsilon
  70.  
  71.     def adagrad(self, x, gradient_x, G, init_lr):
  72.         """
  73.         adagrad算法更新参数，G为参数梯度平方的累计值。
  74.         """
  75.         G += gradient_x ** 2
  76.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  77.         return x, G
  78.  
  79.     def step(self):
  80.         """
  81.         参数更新
  82.         """
  83.         for key in self.model.params.keys():
  84.             self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
  85.                                                                self.model.grads[key],
  86.                                                                self.G[key],
  87.                                                                self.init_lr)
  88.  
  89.  
  90. class RMSprop(Optimizer):
  91.     def __init__(self, init_lr, model, beta, epsilon):
  92.         """
  93.         RMSprop优化器初始化
  94.         输入：
  95.             - init_lr：初始学习率
  96.             - model：模型，model.params存储模型参数值
  97.             - beta：衰减率
  98.             - epsilon：保持数值稳定性而设置的常数
  99.         """
  100.         super(RMSprop, self).__init__(init_lr=init_lr, model=model)
  101.         self.G = {}
  102.         for key in self.model.params.keys():
  103.             self.G[key] = 0
  104.         self.beta = beta
  105.         self.epsilon = epsilon
  106.  
  107.     def rmsprop(self, x, gradient_x, G, init_lr):
  108.         """
  109.         rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
  110.         """
  111.         G = self.beta * G + (1 - self.beta) * gradient_x ** 2
  112.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  113.         return x, G
  114.  
  115.     def step(self):
  116.         """参数更新"""
  117.         for key in self.model.params.keys():
  118.             self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
  119.                                                                self.model.grads[key],
  120.                                                                self.G[key],
  121.                                                                self.init_lr)
  122.  
  123.  
  124. class Momentum(Optimizer):
  125.     def __init__(self, init_lr, model, rho):
  126.         """
  127.         Momentum优化器初始化
  128.         输入：
  129.             - init_lr：初始学习率
  130.             - model：模型，model.params存储模型参数值
  131.             - rho：动量因子
  132.         """
  133.         super(Momentum, self).__init__(init_lr=init_lr, model=model)
  134.         self.delta_x = {}
  135.         for key in self.model.params.keys():
  136.             self.delta_x[key] = 0
  137.         self.rho = rho
  138.  
  139.     def momentum(self, x, gradient_x, delta_x, init_lr):
  140.         """
  141.         momentum算法更新参数，delta_x为梯度的加权移动平均
  142.         """
  143.         delta_x = self.rho * delta_x - init_lr * gradient_x
  144.         x += delta_x
  145.         return x, delta_x
  146.  
  147.     def step(self):
  148.         """参数更新"""
  149.         for key in self.model.params.keys():
  150.             self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
  151.                                                                       self.model.grads[key],
  152.                                                                       self.delta_x[key],
  153.                                                                       self.init_lr)
  154.  
  155.  
  156. class Adam(Optimizer):
  157.     def __init__(self, init_lr, model, beta1, beta2, epsilon):
  158.         """
  159.         Adam优化器初始化
  160.         输入：
  161.             - init_lr：初始学习率
  162.             - model：模型，model.params存储模型参数值
  163.             - beta1, beta2：移动平均的衰减率
  164.             - epsilon：保持数值稳定性而设置的常数
  165.         """
  166.         super(Adam, self).__init__(init_lr=init_lr, model=model)
  167.         self.beta1 = beta1
  168.         self.beta2 = beta2
  169.         self.epsilon = epsilon
  170.         self.M, self.G = {}, {}
  171.         for key in self.model.params.keys():
  172.             self.M[key] = 0
  173.             self.G[key] = 0
  174.         self.t = 1
  175.  
  176.     def adam(self, x, gradient_x, G, M, t, init_lr):
  177.         """
  178.         adam算法更新参数
  179.         输入：
  180.             - x：参数
  181.             - G：梯度平方的加权移动平均
  182.             - M：梯度的加权移动平均
  183.             - t：迭代次数
  184.             - init_lr：初始学习率
  185.         """
  186.         M = self.beta1 * M + (1 - self.beta1) * gradient_x
  187.         G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
  188.         M_hat = M / (1 - self.beta1 ** t)
  189.         G_hat = G / (1 - self.beta2 ** t)
  190.         t += 1
  191.         x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
  192.         return x, G, M, t
  193.  
  194.     def step(self):
  195.         """参数更新"""
  196.         for key in self.model.params.keys():
  197.             self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
  198.                                                                                  self.model.grads[key],
  199.                                                                                  self.G[key],
  200.                                                                                  self.M[key],
  201.                                                                                  self.t,
  202.                                                                                  self.init_lr)
  203.  
  204. class Nesterov(Optimizer):
  205.     def __init__(self, init_lr, model, rho):
  206.         super(Nesterov, self).__init__(init_lr=init_lr, model=model)
  207.         self.delta_x = {}
  208.         for key in self.model.params.keys():
  209.             self.delta_x[key] = 0
  210.         self.rho = rho
  211.  
  212.     def nesterov(self, x, gradient_x, delta_x, init_lr):
  213.         """
  214.         Nesterov算法更新参数，delta_x为梯度的加权移动平均
  215.         """
  216.         delta_x_prev = delta_x
  217.         delta_x = self.rho * delta_x - init_lr * gradient_x
  218.         x += -self.rho * delta_x_prev + (1 + self.rho) * delta_x
  219.         return x, delta_x
  220.  
  221.  
  222. class OptimizedFunction3D(Op):
  223.     def __init__(self):
  224.         super(OptimizedFunction3D, self).__init__()
  225.         self.params = {'x': 0}
  226.         self.grads = {'x': 0}
  227.  
  228.     def forward(self, x):
  229.         self.params['x'] = x
  230.         return x[0] * x[0] / 20 + x[1] * x[1] / 1  # x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]
  231.  
  232.     def backward(self):
  233.         x = self.params['x']
  234.         gradient1 = 2 * x[0] / 20
  235.         gradient2 = 2 * x[1] / 1
  236.         grad1 = torch.Tensor([gradient1])
  237.         grad2 = torch.Tensor([gradient2])
  238.         self.grads['x'] = torch.cat([grad1, grad2])
  239.  
  240.  
  241. class Visualization3D(animation.FuncAnimation):
  242.     """    绘制动态图像，可视化参数更新轨迹    """
  243.  
  244.     def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=100, blit=True, **kwargs):
  245.         """
  246.         初始化3d可视化类
  247.         输入：
  248.             xy_values：三维中x,y维度的值
  249.             z_values：三维中z维度的值
  250.             labels：每个参数更新轨迹的标签
  251.             colors：每个轨迹的颜色
  252.             interval：帧之间的延迟（以毫秒为单位）
  253.             blit：是否优化绘图
  254.         """
  255.         self.fig = fig
  256.         self.ax = ax
  257.         self.xy_values = xy_values
  258.         self.z_values = z_values
  259.  
  260.         frames = max(xy_value.shape[0] for xy_value in xy_values)
  261.  
  262.         self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]
  263.                       for _, label, color in zip_longest(xy_values, labels, colors)]
  264.         self.points = [ax.plot([], [], [], color=color, markeredgewidth=1, markeredgecolor='black', marker='o')[0]
  265.                        for _, color in zip_longest(xy_values, colors)]
  266.         # print(self.lines)
  267.         super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,
  268.                                               interval=interval, blit=blit, **kwargs)
  269.  
  270.     def init_animation(self):
  271.         # 数值初始化
  272.         for line in self.lines:
  273.             line.set_data_3d([], [], [])
  274.         for point in self.points:
  275.             point.set_data_3d([], [], [])
  276.         return self.points + self.lines
  277.  
  278.     def animate(self, i):
  279.         # 将x,y,z三个数据传入，绘制三维图像
  280.         for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):
  281.             line.set_data_3d(xy_value[:i, 0], xy_value[:i, 1], z_value[:i])
  282.         for point, xy_value, z_value in zip(self.points, self.xy_values, self.z_values):
  283.             point.set_data_3d(xy_value[i, 0], xy_value[i, 1], z_value[i])
  284.         return self.points + self.lines
  285.  
  286.  
  287. def train_f(model, optimizer, x_init, epoch):
  288.     x = x_init
  289.     all_x = []
  290.     losses = []
  291.     for i in range(epoch):
  292.         all_x.append(copy.deepcopy(x.numpy()))  # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.
  293.         loss = model(x)
  294.         losses.append(loss)
  295.         model.backward()
  296.         optimizer.step()
  297.         x = model.params['x']
  298.     return torch.Tensor(np.array(all_x)), losses
  299.  
  300.  
  301. # 构建5个模型，分别配备不同的优化器
  302. model1 = OptimizedFunction3D()
  303. opt_gd = SimpleBatchGD(init_lr=0.95, model=model1)
  304.  
  305. model2 = OptimizedFunction3D()
  306. opt_adagrad = Adagrad(init_lr=1.5, model=model2, epsilon=1e-7)
  307.  
  308. model3 = OptimizedFunction3D()
  309. opt_rmsprop = RMSprop(init_lr=0.05, model=model3, beta=0.9, epsilon=1e-7)
  310.  
  311. model4 = OptimizedFunction3D()
  312. opt_momentum = Momentum(init_lr=0.1, model=model4, rho=0.9)
  313.  
  314. model5 = OptimizedFunction3D()
  315. opt_adam = Adam(init_lr=0.3, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
  316.  
  317. model6 = OptimizedFunction3D()
  318. opt_nesterov = Nesterov(init_lr=0.01, model=model6, rho=0.9)
  319.  
  320. models = [model1, model2, model3, model4, model5, model6]
  321. opts = [opt_gd, opt_adagrad, opt_rmsprop, opt_momentum, opt_adam, opt_nesterov]
  322.  
  323. x_all_opts = []
  324. z_all_opts = []
  325.  
  326. # 使用不同优化器训练
  327.  
  328. for model, opt in zip(models, opts):
  329.     x_init = torch.FloatTensor([-7, 2])
  330.     x_one_opt, z_one_opt = train_f(model, opt, x_init, 100)  # epoch
  331.     # 保存参数值
  332.     x_all_opts.append(x_one_opt.numpy())
  333.     z_all_opts.append(np.squeeze(z_one_opt))
  334.  
  335. # 使用numpy.meshgrid生成x1,x2矩阵，矩阵的每一行为[-3, 3]，以0.1为间隔的数值
  336. x1 = np.arange(-10, 10, 0.01)
  337. x2 = np.arange(-5, 5, 0.01)
  338. x1, x2 = np.meshgrid(x1, x2)
  339. init_x = torch.Tensor(np.array([x1, x2]))
  340.  
  341. model = OptimizedFunction3D()
  342.  
  343. # 绘制 f_3d函数 的 三维图像
  344. fig = plt.figure()
  345. ax = plt.axes(projection='3d')
  346. X = init_x[0].numpy()
  347. Y = init_x[1].numpy()
  348. Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
  349. surf = ax.plot_surface(X, Y, Z, edgecolor='grey', cmap=cm.coolwarm)
  350. # fig.colorbar(surf, shrink=0.5, aspect=1)
  351. # ax.set_zlim(-3, 2)
  352. ax.set_xlabel('x1')
  353. ax.set_ylabel('x2')
  354. ax.set_zlabel('f(x1,x2)')
  355.  
  356. labels = ['SGD', 'AdaGrad', 'RMSprop', 'Momentum', 'Adam','Nesterov']
  357. colors = ['#3b818c', '#f6f237', '#45f637', '#fed71a', '#815c94', '#f97d1c']
  358.  
  359. animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax, interval=100)
  360. ax.legend(loc='upper right')
  361.  
  362. plt.show()
  363. # animator.save('teaser' + '.gif', writer='imagemagick',fps=10) # 效果不好，估计被挡住了…… 有待进一步提高 Edit by David 2022.12.4
  364. # save不好用，不费劲了，安装个软件做gif https://pc.qq.com/detail/13/detail_23913.html

图像如下：

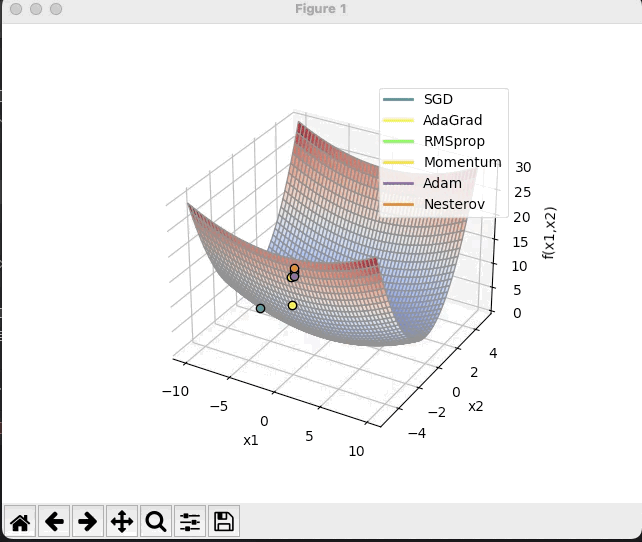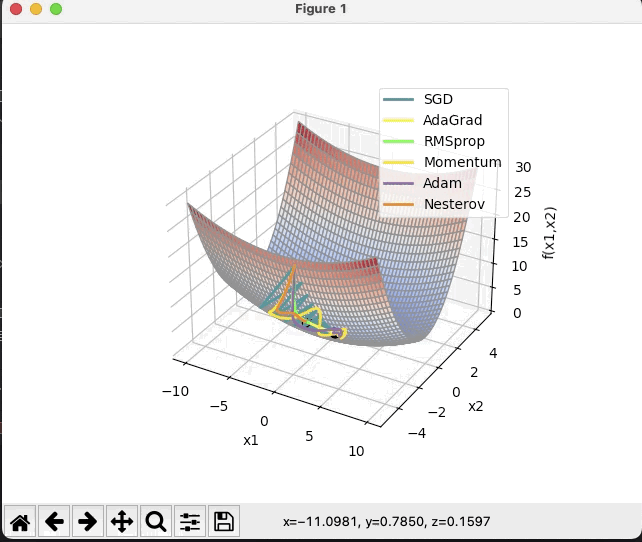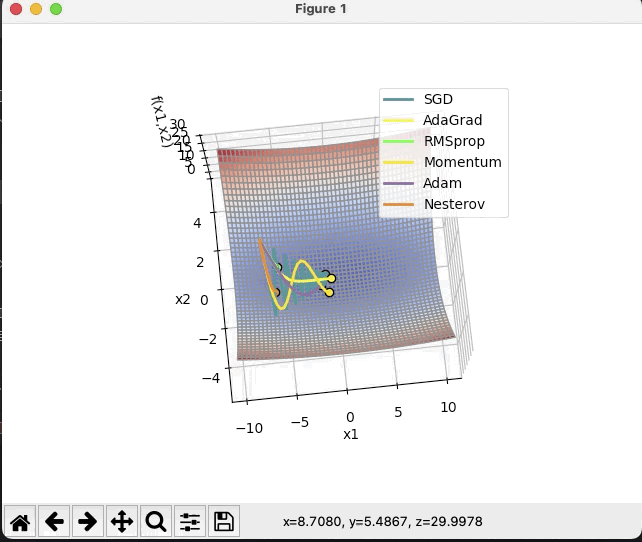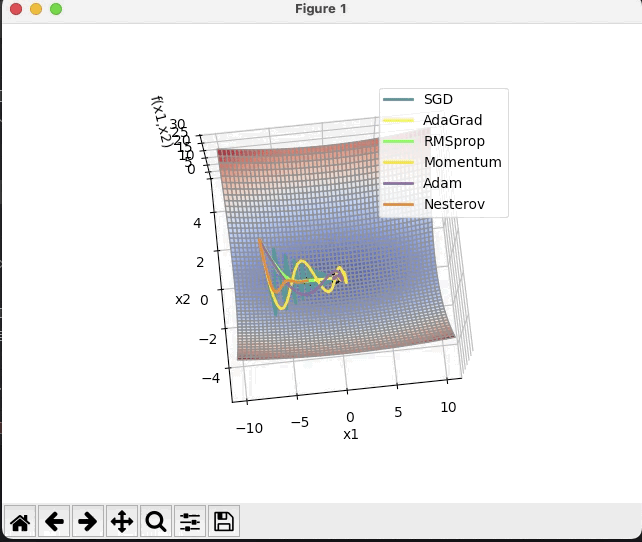
· 结合3D动画，用自己的语言，从轨迹、速度等多个角度讲解各个算法优缺点

特地在两个图用了一样的颜色表示不同算法的轨迹，可以看出：

SGD在图1中速度比较缓慢，但图2中由于在一个坡底，因此左右大幅度晃动，总体来讲比较耗时，可能会停留在鞍点，找不到全局最小值；

adagrad（暗黄）和RMSprop（绿）都属于在SGD基础上的优化，因此在稍微简单的曲面中二者的移动方向基本一致。而图1中可以看出黄线移动一段时间后停止了，绿线沿着黄线的路径继续前进着，而图2可以看出，绿线的速度是没有黄线快的。

分析一下原因：adagrad是通过累计值计算梯度优化学习率的，当累加值变大时学习率逐渐变小，几乎为0，因此最终难以前进；而RMSprop则是通过指数衰减移动平均来改变学习率，可以理解为RMSprop是通过一个移动窗口来计算学习率的，因此它一定程度内不会像adagrad那样缩减至零，但早期移动速度也不会像adagrad那样移动速度特别快。

而Momentum（浅黄）和Nesterov（橘色）则是动量类的经典选手，第一张图可以看出两个动量法都以极高的速度冲出了局部最小值，向着全局最小值的方向去了；图二中可以看出牛顿法比起基础动量法摆动的幅度更小。

3.复现CS231经典动画

代码实现：

  1. import torch
  2. import numpy as np
  3. import copy
  4. from matplotlib import pyplot as plt
  5. from matplotlib import animation
  6. from itertools import zip_longest
  7. from matplotlib import cm
  8.  
  9.  
  10. class Op(object):
  11.     def __init__(self):
  12.         pass
  13.  
  14.     def __call__(self, inputs):
  15.         return self.forward(inputs)
  16.  
  17.     # 输入：张量inputs
  18.     # 输出：张量outputs
  19.     def forward(self, inputs):
  20.         # return outputs
  21.         raise NotImplementedError
  22.  
  23.     # 输入：最终输出对outputs的梯度outputs_grads
  24.     # 输出：最终输出对inputs的梯度inputs_grads
  25.     def backward(self, outputs_grads):
  26.         # return inputs_grads
  27.         raise NotImplementedError
  28.  
  29.  
  30. class Optimizer(object):  # 优化器基类
  31.     def __init__(self, init_lr, model):
  32.         """
  33.         优化器类初始化
  34.         """
  35.         # 初始化学习率，用于参数更新的计算
  36.         self.init_lr = init_lr
  37.         # 指定优化器需要优化的模型
  38.         self.model = model
  39.  
  40.     def step(self):
  41.         """
  42.         定义每次迭代如何更新参数
  43.         """
  44.         pass
  45.  
  46.  
  47. class SimpleBatchGD(Optimizer):
  48.     def __init__(self, init_lr, model):
  49.         super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
  50.  
  51.     def step(self):
  52.         # 参数更新
  53.         if isinstance(self.model.params, dict):
  54.             for key in self.model.params.keys():
  55.                 self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]
  56.  
  57.  
  58. class Adagrad(Optimizer):
  59.     def __init__(self, init_lr, model, epsilon):
  60.         """
  61.         Adagrad 优化器初始化
  62.         输入：
  63.             - init_lr： 初始学习率 - model：模型，model.params存储模型参数值  - epsilon：保持数值稳定性而设置的非常小的常数
  64.         """
  65.         super(Adagrad, self).__init__(init_lr=init_lr, model=model)
  66.         self.G = {}
  67.         for key in self.model.params.keys():
  68.             self.G[key] = 0
  69.         self.epsilon = epsilon
  70.  
  71.     def adagrad(self, x, gradient_x, G, init_lr):
  72.         """
  73.         adagrad算法更新参数，G为参数梯度平方的累计值。
  74.         """
  75.         G += gradient_x ** 2
  76.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  77.         return x, G
  78.  
  79.     def step(self):
  80.         """
  81.         参数更新
  82.         """
  83.         for key in self.model.params.keys():
  84.             self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
  85.                                                                self.model.grads[key],
  86.                                                                self.G[key],
  87.                                                                self.init_lr)
  88.  
  89.  
  90. class RMSprop(Optimizer):
  91.     def __init__(self, init_lr, model, beta, epsilon):
  92.         """
  93.         RMSprop优化器初始化
  94.         输入：
  95.             - init_lr：初始学习率
  96.             - model：模型，model.params存储模型参数值
  97.             - beta：衰减率
  98.             - epsilon：保持数值稳定性而设置的常数
  99.         """
  100.         super(RMSprop, self).__init__(init_lr=init_lr, model=model)
  101.         self.G = {}
  102.         for key in self.model.params.keys():
  103.             self.G[key] = 0
  104.         self.beta = beta
  105.         self.epsilon = epsilon
  106.  
  107.     def rmsprop(self, x, gradient_x, G, init_lr):
  108.         """
  109.         rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
  110.         """
  111.         G = self.beta * G + (1 - self.beta) * gradient_x ** 2
  112.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  113.         return x, G
  114.  
  115.     def step(self):
  116.         """参数更新"""
  117.         for key in self.model.params.keys():
  118.             self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
  119.                                                                self.model.grads[key],
  120.                                                                self.G[key],
  121.                                                                self.init_lr)
  122.  
  123.  
  124. class Momentum(Optimizer):
  125.     def __init__(self, init_lr, model, rho):
  126.         """
  127.         Momentum优化器初始化
  128.         输入：
  129.             - init_lr：初始学习率
  130.             - model：模型，model.params存储模型参数值
  131.             - rho：动量因子
  132.         """
  133.         super(Momentum, self).__init__(init_lr=init_lr, model=model)
  134.         self.delta_x = {}
  135.         for key in self.model.params.keys():
  136.             self.delta_x[key] = 0
  137.         self.rho = rho
  138.  
  139.     def momentum(self, x, gradient_x, delta_x, init_lr):
  140.         """
  141.         momentum算法更新参数，delta_x为梯度的加权移动平均
  142.         """
  143.         delta_x = self.rho * delta_x - init_lr * gradient_x
  144.         x += delta_x
  145.         return x, delta_x
  146.  
  147.     def step(self):
  148.         """参数更新"""
  149.         for key in self.model.params.keys():
  150.             self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
  151.                                                                       self.model.grads[key],
  152.                                                                       self.delta_x[key],
  153.                                                                       self.init_lr)
  154.  
  155.  
  156. class Adam(Optimizer):
  157.     def __init__(self, init_lr, model, beta1, beta2, epsilon):
  158.         """
  159.         Adam优化器初始化
  160.         输入：
  161.             - init_lr：初始学习率
  162.             - model：模型，model.params存储模型参数值
  163.             - beta1, beta2：移动平均的衰减率
  164.             - epsilon：保持数值稳定性而设置的常数
  165.         """
  166.         super(Adam, self).__init__(init_lr=init_lr, model=model)
  167.         self.beta1 = beta1
  168.         self.beta2 = beta2
  169.         self.epsilon = epsilon
  170.         self.M, self.G = {}, {}
  171.         for key in self.model.params.keys():
  172.             self.M[key] = 0
  173.             self.G[key] = 0
  174.         self.t = 1
  175.  
  176.     def adam(self, x, gradient_x, G, M, t, init_lr):
  177.         """
  178.         adam算法更新参数
  179.         输入：
  180.             - x：参数
  181.             - G：梯度平方的加权移动平均
  182.             - M：梯度的加权移动平均
  183.             - t：迭代次数
  184.             - init_lr：初始学习率
  185.         """
  186.         M = self.beta1 * M + (1 - self.beta1) * gradient_x
  187.         G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
  188.         M_hat = M / (1 - self.beta1 ** t)
  189.         G_hat = G / (1 - self.beta2 ** t)
  190.         t += 1
  191.         x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
  192.         return x, G, M, t
  193.  
  194.     def step(self):
  195.         """参数更新"""
  196.         for key in self.model.params.keys():
  197.             self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
  198.                                                                                  self.model.grads[key],
  199.                                                                                  self.G[key],
  200.                                                                                  self.M[key],
  201.                                                                                  self.t,
  202.                                                                                  self.init_lr)
  203.  
  204. class Nesterov(Optimizer):
  205.     def __init__(self, init_lr, model, rho):
  206.         super(Nesterov, self).__init__(init_lr=init_lr, model=model)
  207.         self.delta_x = {}
  208.         for key in self.model.params.keys():
  209.             self.delta_x[key] = 0
  210.         self.rho = rho
  211.  
  212.     def nesterov(self, x, gradient_x, delta_x, init_lr):
  213.         """
  214.         Nesterov算法更新参数，delta_x为梯度的加权移动平均
  215.         """
  216.         delta_x_prev = delta_x
  217.         delta_x = self.rho * delta_x - init_lr * gradient_x
  218.         x += -self.rho * delta_x_prev + (1 + self.rho) * delta_x
  219.         return x, delta_x
  220.  
  221.     def step(self):
  222.         """参数更新"""
  223.         for key in self.model.params.keys():
  224.             self.model.params[key], self.delta_x[key] = self.nesterov(self.model.params[key],
  225.                                                                       self.model.grads[key],
  226.                                                                       self.delta_x[key],
  227.                                                                       self.init_lr)
  228.  
  229.  
  230. class OptimizedFunction3D(Op):
  231.     def __init__(self):
  232.         super(OptimizedFunction3D, self).__init__()
  233.         self.params = {'x': 0}
  234.         self.grads = {'x': 0}
  235.  
  236.     def forward(self, x):
  237.         self.params['x'] = x
  238.         return - x[0] * x[0] / 2 + x[1] * x[1] / 1  # x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]
  239.  
  240.     def backward(self):
  241.         x = self.params['x']
  242.         gradient1 = - 2 * x[0] / 2
  243.         gradient2 = 2 * x[1] / 1
  244.         grad1 = torch.Tensor([gradient1])
  245.         grad2 = torch.Tensor([gradient2])
  246.         self.grads['x'] = torch.cat([grad1, grad2])
  247.  
  248.  
  249. class Visualization3D(animation.FuncAnimation):
  250.     """    绘制动态图像，可视化参数更新轨迹    """
  251.  
  252.     def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=100, blit=True, **kwargs):
  253.         """
  254.         初始化3d可视化类
  255.         输入：
  256.             xy_values：三维中x,y维度的值
  257.             z_values：三维中z维度的值
  258.             labels：每个参数更新轨迹的标签
  259.             colors：每个轨迹的颜色
  260.             interval：帧之间的延迟（以毫秒为单位）
  261.             blit：是否优化绘图
  262.         """
  263.         self.fig = fig
  264.         self.ax = ax
  265.         self.xy_values = xy_values
  266.         self.z_values = z_values
  267.  
  268.         frames = max(xy_value.shape[0] for xy_value in xy_values)
  269.  
  270.         self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]
  271.                       for _, label, color in zip_longest(xy_values, labels, colors)]
  272.         self.points = [ax.plot([], [], [], color=color, markeredgewidth=1, markeredgecolor='black', marker='o')[0]
  273.                        for _, color in zip_longest(xy_values, colors)]
  274.         # print(self.lines)
  275.         super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,
  276.                                               interval=interval, blit=blit, **kwargs)
  277.  
  278.     def init_animation(self):
  279.         # 数值初始化
  280.         for line in self.lines:
  281.             line.set_data_3d([], [], [])
  282.         for point in self.points:
  283.             point.set_data_3d([], [], [])
  284.         return self.points + self.lines
  285.  
  286.     def animate(self, i):
  287.         # 将x,y,z三个数据传入，绘制三维图像
  288.         for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):
  289.             line.set_data_3d(xy_value[:i, 0], xy_value[:i, 1], z_value[:i])
  290.         for point, xy_value, z_value in zip(self.points, self.xy_values, self.z_values):
  291.             point.set_data_3d(xy_value[i, 0], xy_value[i, 1], z_value[i])
  292.         return self.points + self.lines
  293.  
  294.  
  295. def train_f(model, optimizer, x_init, epoch):
  296.     x = x_init
  297.     all_x = []
  298.     losses = []
  299.     for i in range(epoch):
  300.         all_x.append(copy.deepcopy(x.numpy()))  # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.
  301.         loss = model(x)
  302.         losses.append(loss)
  303.         model.backward()
  304.         optimizer.step()
  305.         x = model.params['x']
  306.     return torch.Tensor(np.array(all_x)), losses
  307.  
  308.  
  309. # 构建6个模型，分别配备不同的优化器
  310. model1 = OptimizedFunction3D()
  311. opt_gd = SimpleBatchGD(init_lr=0.05, model=model1)
  312.  
  313. model2 = OptimizedFunction3D()
  314. opt_adagrad = Adagrad(init_lr=0.05, model=model2, epsilon=1e-7)
  315.  
  316. model3 = OptimizedFunction3D()
  317. opt_rmsprop = RMSprop(init_lr=0.05, model=model3, beta=0.9, epsilon=1e-7)
  318.  
  319. model4 = OptimizedFunction3D()
  320. opt_momentum = Momentum(init_lr=0.05, model=model4, rho=0.9)
  321.  
  322. model5 = OptimizedFunction3D()
  323. opt_adam = Adam(init_lr=0.05, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
  324.  
  325. model6 = OptimizedFunction3D()
  326. opt_nesterov = Nesterov(init_lr=0.01, model=model6, rho=0.9)
  327.  
  328.  
  329. models = [model6, model5, model2, model3, model4, model1]
  330. opts = [opt_nesterov,opt_adam, opt_adagrad, opt_rmsprop, opt_momentum, opt_gd]
  331.  
  332. x_all_opts = []
  333. z_all_opts = []
  334.  
  335. # 使用不同优化器训练
  336.  
  337. for model, opt in zip(models, opts):
  338.     x_init = torch.FloatTensor([0.00001, 0.5])
  339.     x_one_opt, z_one_opt = train_f(model, opt, x_init, 100)  # epoch
  340.     # 保存参数值
  341.     x_all_opts.append(x_one_opt.numpy())
  342.     z_all_opts.append(np.squeeze(z_one_opt))
  343.  
  344. # 使用numpy.meshgrid生成x1,x2矩阵，矩阵的每一行为[-3, 3]，以0.1为间隔的数值
  345. x1 = np.arange(-1, 2, 0.01)
  346. x2 = np.arange(-1, 1, 0.05)
  347. x1, x2 = np.meshgrid(x1, x2)
  348. init_x = torch.Tensor(np.array([x1, x2]))
  349.  
  350. model = OptimizedFunction3D()
  351.  
  352. # 绘制 f_3d函数 的 三维图像
  353. fig = plt.figure()
  354. ax = plt.axes(projection='3d')
  355. X = init_x[0].numpy()
  356. Y = init_x[1].numpy()
  357. Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
  358. surf = ax.plot_surface(X, Y, Z, edgecolor='grey', cmap=cm.coolwarm)
  359. # fig.colorbar(surf, shrink=0.5, aspect=1)
  360. ax.set_zlim(-3, 2)
  361. ax.set_xlabel('x1')
  362. ax.set_ylabel('x2')
  363. ax.set_zlabel('f(x1,x2)')
  364.  
  365. labels = ['Adam', 'AdaGrad', 'RMSprop', 'Momentum', 'SGD','Nesterov']
  366. colors = ['#3b818c', '#f6f237', '#45f637', '#fed71a', '#815c94', '#f97d1c']
  367.  
  368. animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)
  369. ax.legend(loc='upper right')
  370.  
  371. plt.show()
  372. # animator.save('teaser' + '.gif', writer='imagemagick',fps=10) # 效果不好，估计被挡住了…… 有待进一步提高 Edit by David 2022.12.4
  373. # save不好用，不费劲了，安装个软件做gif https://pc.qq.com/detail/13/detail_23913.html

图像实现：


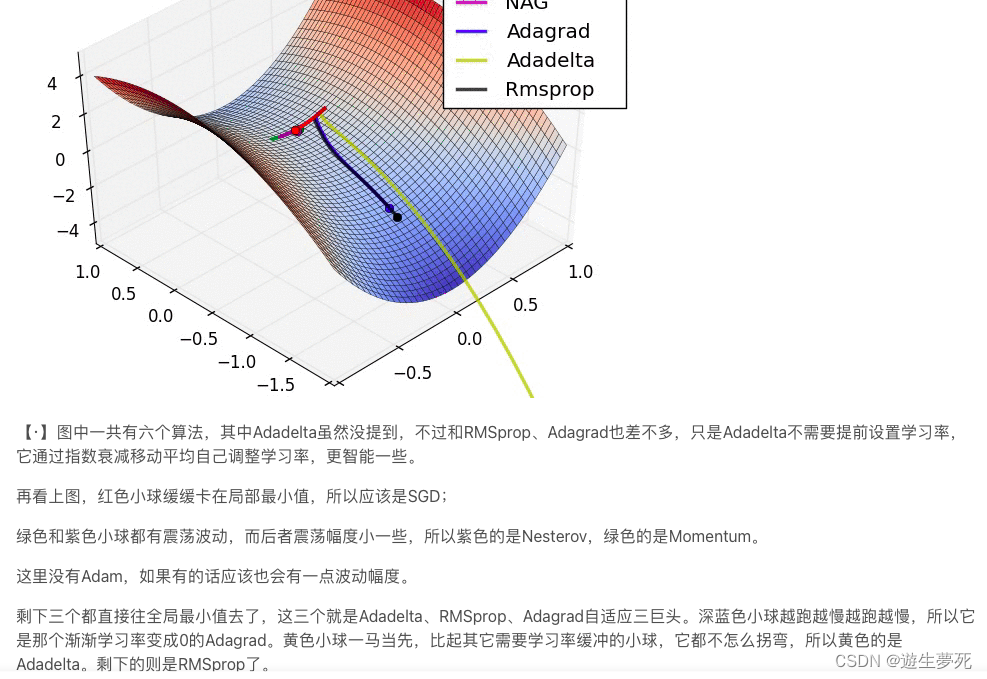
结合3D动画，用自己的语言，从轨迹、速度等多个角度讲解各个算法优缺点

上图的颜色还是和前两个图一样，可以直观地看出算法的差异来，但优缺点我就不讲了，因为在上个作业12已经说过了。

·心得总结

说来也巧，本来写作业12的时候想着概念都说了，上课讲过的那个动图也顺便说说分析分析吧，结果写完再看作业13，发现原来讲动图的任务在这里……

不过个人感觉我作业12写的确实挺好，各个算法的优缺点、动图的分析，在作业12都已经说过了，也查阅了很多文献很多资料，以至于在作业13没什么想说的了。

这次作业13我也做了一些优化，比如在图里加了“Nesterov”算法的曲线，在每个图都用相同的颜色表示轨迹。应该可以通过第3个实验返回去优化一下第1个实验的，但复习要紧，我还是先去复习吧。

至于期末总结部分，一个舍友说只用写心得，一个舍友说需要写知识点的总结，我想着那就等快考深度学习的时候再做总结吧，总结知识点+心得，顺便复习了。

参考文献：

http://iyenn.com/rec/2011766.html?spm=1001.2014.3001.5502

NNDL实验 优化算法3D轨迹 复现cs231经典动画_深度学习 优化算法 动画展示-CSDN博客

注：本文转载自blog.csdn.net的我为社会扛大旗的文章"https://blog.csdn.net/qq_62591797/article/details/135332869"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！