NNDL 作业12 优化算法2D可视化

目录

简要介绍图中的优化算法，编程实现并2D可视化

·被优化函数 （x2）

·对函数的实现及分析

1.SGD

2.Adagrad（自适应梯度优化）

3.RMSprop

4.Momentum

5.Adam（自适应矩估计）

·被优化函数  （x、y）

代码及实现

·猜一猜

6.Nesterov（牛顿动量算法）

· 解释不同轨迹的形成原因

·分析各个轨迹的原因

·猜一猜谜底揭晓

·再训练，再讲解

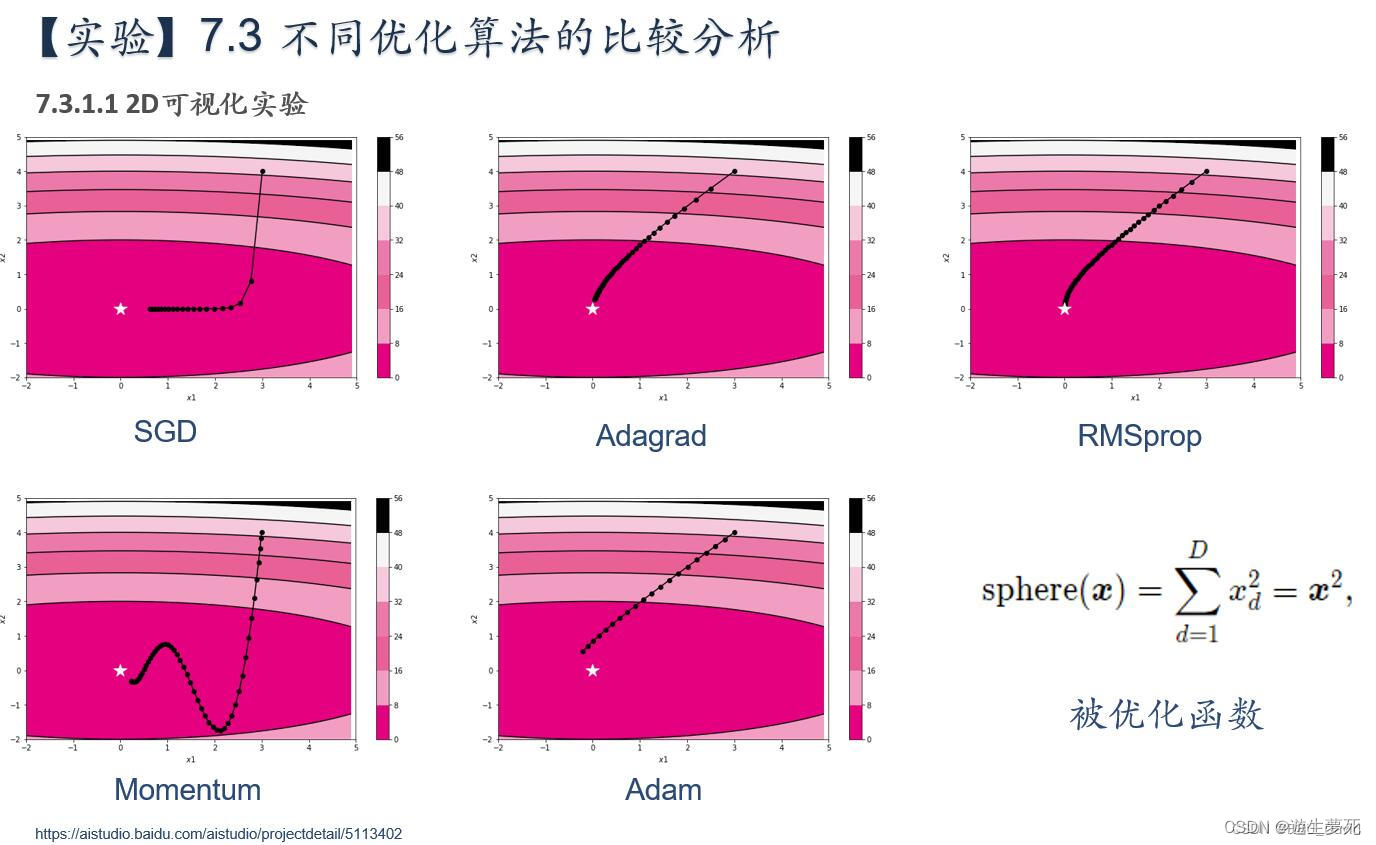
简要介绍图中的优化算法，编程实现并2D可视化


·被优化函数 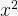x^{2}（x2）

·对函数的实现及分析
  1. import numpy as np
  2. from matplotlib import pyplot as plt
  3.  
  4.  
  5. # https://blog.csdn.net/weixin_39228381/article/details/108511882
  6.  
  7. def func(x, y):
  8.     return x * x
  9.  
  10.  
  11. def paint_loss_func():
  12.     x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
  13.     y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数
  14.  
  15.     X, Y = np.meshgrid(x, y)
  16.     Z = func(X, Y)
  17.  
  18.     fig, ax = plt.subplots(subplot_kw={'projection': '3d'})
  19.     plt.xlabel('x')
  20.     plt.ylabel('y')
  21.  
  22.     ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
  23.     plt.show()
  24.  
  25.  
  26. if __name__ == "__main__":
  27.     paint_loss_func()

对函数x^2实现函数后呈递出的图像如下图所示：

由于该函数只在x方向有改变，因此更像一个被握折起的纸，中间平坦整个图像向下弯曲，因此x=0的一条直线上均是最低点。

而我们将实现的共有5个不同优化算法，接下来分别对这些代码展开解释与实现：

实现代码如下：

  1. import torch
  2. from abc import abstractmethod
  3.  
  4.  
  5. class Op(object):
  6.     def __init__(self):
  7.         pass
  8.  
  9.     def __call__(self, inputs):
  10.         return self.forward(inputs)
  11.  
  12.     # 输入：张量inputs
  13.     # 输出：张量outputs
  14.     def forward(self, inputs):
  15.         # return outputs
  16.         raise NotImplementedError
  17.  
  18.     # 输入：最终输出对outputs的梯度outputs_grads
  19.     # 输出：最终输出对inputs的梯度inputs_grads
  20.     def backward(self, outputs_grads):
  21.         # return inputs_grads
  22.         raise NotImplementedError
  23.  
  24.  
  25. # 优化器基类
  26. class Optimizer(object):
  27.     def __init__(self, init_lr, model):
  28.         """
  29.         优化器类初始化
  30.         """
  31.         # 初始化学习率，用于参数更新的计算
  32.         self.init_lr = init_lr
  33.         # 指定优化器需要优化的模型
  34.         self.model = model
  35.  
  36.     @abstractmethod
  37.     def step(self):
  38.         """
  39.         定义每次迭代如何更新参数
  40.         """
  41.         pass
  42.  
  43.  
  44. class SimpleBatchGD(Optimizer):
  45.     def __init__(self, init_lr, model):
  46.         super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
  47.  
  48.     def step(self):
  49.         # 参数更新
  50.         if isinstance(self.model.params, dict):
  51.             for key in self.model.params.keys():
  52.                 self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]
  53.  
  54.  
  55. class Adagrad(Optimizer):
  56.     def __init__(self, init_lr, model, epsilon):
  57.         super(Adagrad, self).__init__(init_lr=init_lr, model=model)
  58.         self.G = {}
  59.         for key in self.model.params.keys():
  60.             self.G[key] = 0
  61.         self.epsilon = epsilon
  62.  
  63.     def adagrad(self, x, gradient_x, G, init_lr):
  64.         G += gradient_x ** 2
  65.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  66.         return x, G
  67.  
  68.     def step(self):
  69.         for key in self.model.params.keys():
  70.             self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
  71.                                                                self.model.grads[key],
  72.                                                                self.G[key],
  73.                                                                self.init_lr)
  74.  
  75.  
  76. class RMSprop(Optimizer):
  77.     def __init__(self, init_lr, model, beta, epsilon):
  78.         super(RMSprop, self).__init__(init_lr=init_lr, model=model)
  79.         self.G = {}
  80.         for key in self.model.params.keys():
  81.             self.G[key] = 0
  82.         self.beta = beta
  83.         self.epsilon = epsilon
  84.  
  85.     def rmsprop(self, x, gradient_x, G, init_lr):
  86.         """
  87.         rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
  88.         """
  89.         G = self.beta * G + (1 - self.beta) * gradient_x ** 2
  90.         x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
  91.         return x, G
  92.  
  93.     def step(self):
  94.         """参数更新"""
  95.         for key in self.model.params.keys():
  96.             self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
  97.                                                                self.model.grads[key],
  98.                                                                self.G[key],
  99.                                                                self.init_lr)
  100.  
  101.  
  102. class Momentum(Optimizer):
  103.     def __init__(self, init_lr, model, rho):
  104.         super(Momentum, self).__init__(init_lr=init_lr, model=model)
  105.         self.delta_x = {}
  106.         for key in self.model.params.keys():
  107.             self.delta_x[key] = 0
  108.         self.rho = rho
  109.  
  110.     def momentum(self, x, gradient_x, delta_x, init_lr):
  111.         """
  112.         momentum算法更新参数，delta_x为梯度的加权移动平均
  113.         """
  114.         delta_x = self.rho * delta_x - init_lr * gradient_x
  115.         x += delta_x
  116.         return x, delta_x
  117.  
  118.     def step(self):
  119.         """参数更新"""
  120.         for key in self.model.params.keys():
  121.             self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
  122.                                                                       self.model.grads[key],
  123.                                                                       self.delta_x[key],
  124.                                                                       self.init_lr)
  125.  
  126.  
  127. class Adam(Optimizer):
  128.     def __init__(self, init_lr, model, beta1, beta2, epsilon):
  129.         super(Adam, self).__init__(init_lr=init_lr, model=model)
  130.         self.beta1 = beta1
  131.         self.beta2 = beta2
  132.         self.epsilon = epsilon
  133.         self.M, self.G = {}, {}
  134.         for key in self.model.params.keys():
  135.             self.M[key] = 0
  136.             self.G[key] = 0
  137.         self.t = 1
  138.  
  139.     def adam(self, x, gradient_x, G, M, t, init_lr):
  140.         M = self.beta1 * M + (1 - self.beta1) * gradient_x
  141.         G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
  142.         M_hat = M / (1 - self.beta1 ** t)
  143.         G_hat = G / (1 - self.beta2 ** t)
  144.         t += 1
  145.         x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
  146.         return x, G, M, t
  147.  
  148.     def step(self):
  149.         """参数更新"""
  150.         for key in self.model.params.keys():
  151.             self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
  152.                                                                                  self.model.grads[key],
  153.                                                                                  self.G[key],
  154.                                                                                  self.M[key],
  155.                                                                                  self.t,
  156.                                                                                  self.init_lr)
  1. from matplotlib import pyplot as plt
  2. from function import *
  3.  
  4. class OptimizedFunction(Op):
  5.     def __init__(self, w):
  6.         super(OptimizedFunction, self).__init__()
  7.         self.w = w
  8.         self.params = {'x': 0}
  9.         self.grads = {'x': 0}
  10.  
  11.     def forward(self, x):
  12.         self.params['x'] = x
  13.         return torch.matmul(self.w.T, torch.tensor(torch.square(self.params['x']), dtype=torch.float32))
  14.  
  15.     def backward(self):
  16.         self.grads['x'] = 2 * torch.multiply(self.w.T, self.params['x'])
  17.  
  18.  
  19. import copy
  20.  
  21.  
  22. def train_f(model, optimizer, x_init, epoch):
  23.     """
  24.     训练函数
  25.     输入：
  26.         - model：被优化函数
  27.         - optimizer：优化器
  28.         - x_init：x初始值
  29.         - epoch：训练回合数
  30.     """
  31.     x = x_init
  32.     all_x = []
  33.     losses = []
  34.     for i in range(epoch):
  35.         all_x.append(copy.copy(x.numpy()))
  36.         loss = model(x)
  37.         losses.append(loss)
  38.         model.backward()
  39.         optimizer.step()
  40.         x = model.params['x']
  41.         # print(all_x)
  42.     return torch.tensor(all_x), losses
  43.  
  44.  
  45. class Visualization(object):
  46.     def __init__(self):
  47.         """
  48.         初始化可视化类
  49.         """
  50.         # 只画出参数x1和x2在区间[-5, 5]的曲线部分
  51.         x1 = np.arange(-5, 5, 0.1)
  52.         x2 = np.arange(-5, 5, 0.1)
  53.         x1, x2 = np.meshgrid(x1, x2)
  54.         self.init_x = torch.tensor([x1, x2])
  55.  
  56.     def plot_2d(self, model, x, fig_name):
  57.         """
  58.         可视化参数更新轨迹
  59.         """
  60.         fig, ax = plt.subplots(figsize=(10, 6))
  61.         cp = ax.contourf(self.init_x[0], self.init_x[1], model(self.init_x.transpose(0, 1)),
  62.                          colors=['#e4007f', '#f19ec2', '#e86096', '#eb7aaa', '#f6c8dc', '#f5f5f5', '#000000'])
  63.         '''
  64.         这行代码使用contourf方法绘制了一个填充的等高线图。
  65.         self.init_x[0]和self.init_x[1]是x1和x2的网格点。
  66.         model(self.init_x.transpose([1, 0, 2]))表示将self.init_x转置后传递给模型函数，得到每个网格点的值。
  67.         colors=['#e4007f', ...]定义了等高线填充的颜色。
  68.         '''
  69.         c = ax.contour(self.init_x[0], self.init_x[1], model(self.init_x.transpose(0, 1)), colors='black')
  70.         # 绘制了等高线的轮廓线，其颜色为黑色
  71.         cbar = fig.colorbar(cp)  # 创建了一个颜色条，与填充的等高线图相关联
  72.         ax.plot(x[:, 0], x[:, 1], '-o', color='#000000')  # 不断更新的x,y绘制点，连成线
  73.         ax.plot(0, 'r*', markersize=18, color='#fefefe')  # 标记0，0点
  74.  
  75.         ax.set_xlabel('$x1$')  # 标签名称
  76.         ax.set_ylabel('$x2$')
  77.  
  78.         ax.set_xlim((-2, 5))  # 标签范围
  79.         ax.set_ylim((-2, 5))
  80.         plt.savefig(fig_name)
  81.         plt.show()
  82.  
  83.  
  84. import numpy as np
  85.  
  86.  
  87. def train_and_plot_f(model, optimizer, epoch, fig_name):
  88.     """
  89.     训练模型并可视化参数更新轨迹
  90.     """
  91.     # 设置x的初始值
  92.     x_init = torch.tensor([3, 4], dtype=torch.float32)  # 初始值在这确定的
  93.     #  print('x1 initiate: {}, x2 initiate: {}'.format(x_init[0].numpy(), x_init[1].numpy()))
  94.     x, losses = train_f(model, optimizer, x_init, epoch)
  95.     # print(x)
  96.     losses = np.array(losses)
  97.  
  98.     # 展示x1、x2的更新轨迹
  99.     vis = Visualization()
  100.     vis.plot_2d(model, x, fig_name)
  101.  
  102.  
  103. # 固定随机种子
  104. torch.seed()
  105. w = torch.as_tensor([0.2, 2])
  106. model = OptimizedFunction(w)
  107. opt = SimpleBatchGD(init_lr=0.2, model=model)
  108. train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para.pdf')
  109.  
  110. # 固定随机种子
  111. torch.seed()
  112. w = torch.as_tensor([0.2, 2])
  113. model2 = OptimizedFunction(w)
  114. opt2 = Adagrad(init_lr=0.5, model=model2, epsilon=1e-7)
  115. train_and_plot_f(model2, opt2, epoch=50, fig_name='opti-vis-para2.pdf')
  116.  
  117. torch.seed()
  118. w = torch.as_tensor([0.2, 2])
  119. model3 = OptimizedFunction(w)
  120. opt3 = RMSprop(init_lr=0.1, model=model3, beta=0.9, epsilon=1e-7)
  121. train_and_plot_f(model3, opt3, epoch=50, fig_name='opti-vis-para3.pdf')
  122.  
  123. # 固定随机种子
  124. torch.seed()
  125. w = torch.as_tensor([0.2, 2])
  126. model4 = OptimizedFunction(w)
  127. opt4 = Momentum(init_lr=0.01, model=model4, rho=0.9)
  128. train_and_plot_f(model4, opt4, epoch=50, fig_name='opti-vis-para4.pdf')
  129.  
  130. # 固定随机种子
  131. torch.seed()
  132. w = torch.as_tensor([0.2, 2])
  133. model5 = OptimizedFunction(w)
  134. opt5 = Adam(init_lr=0.2, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
  135. train_and_plot_f(model5, opt5, epoch=20, fig_name='opti-vis-para5.pdf')


1.SGD

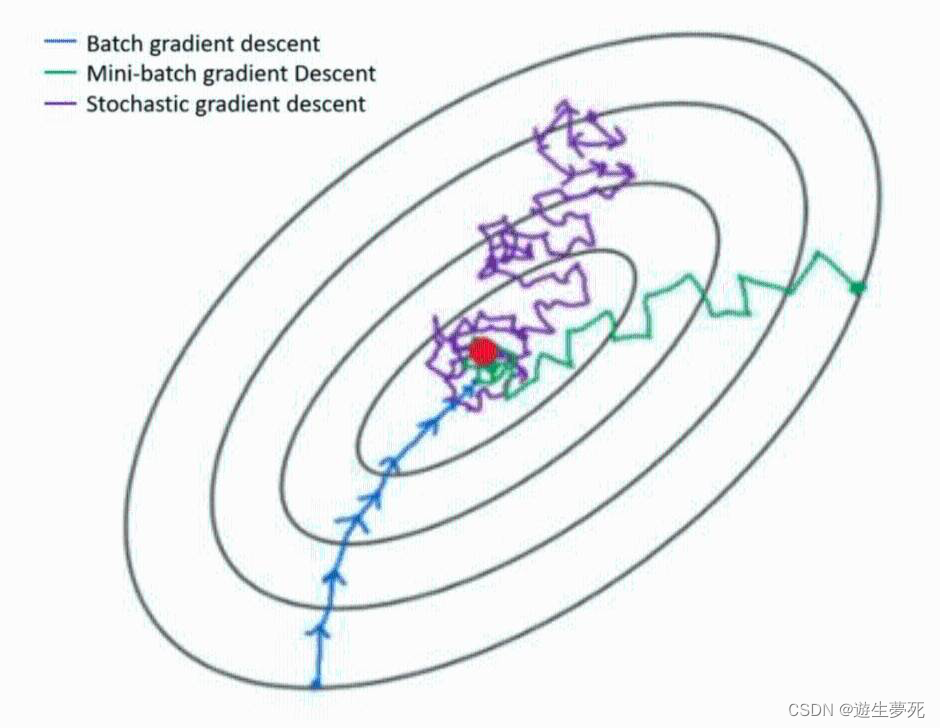
简述：GD是梯度下降法，BGD是批量梯度下降法，MBGD是小批量梯度下降法，而SGD则是随机梯度下降法，在小批量中随机抽取一个样本更新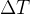\Delta T（即梯度）。随机梯度下降法正像下图所示，是一个平滑降低、通过降低梯度逐渐下降至最优值的过程。

·优缺点：

①优点：SGD的优化会每次随机向一个方向跳动，易于跳出局部最小值，且因为一次迭代只需对一个样本进行计算，所以运行速度很快。

②缺点：如上图所示，BGD、MBGD、SGD的优化轨迹不同，前两者会更加直接地到达最低点，而SGD则会在最小值的周围波动很久，很难达到收敛。而且SGD一次只处理一个样本，因此效率不是很高。

图像：

2.Adagrad（自适应梯度优化）

简述：从图像可以看出，Adagrad可以直接向着最小值的方向优化，它具有可以自适应调整学习率的功能。通过计算每个参数的梯度平方的累计值，再将累计值当做被除数，累计值越大，则梯度逐渐变小，因此Adagrad的梯度变化是一个从大到小的过程，且越来越接近最小值。

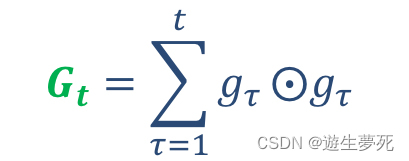
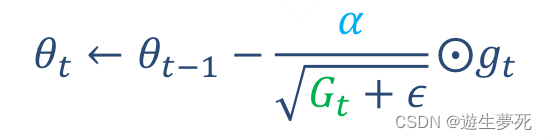
上下两个图从本质上讲是同样的含义

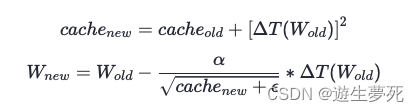
·优缺点：

①优点：可以自动调节学习率，很便捷，很智能；可以直接向着优化方向去，不像SGD会哪个方向都跑跑，Adagrad就是方向找得很准，效率高一些；且这个算法会在数据比较稀疏的时候有很好的效果，跑得很快。

②缺点：由于平方不能为负，因此缓存将始终增加一定的量。因此每个权重的学习率最终都会降低到非常低的值(会到0)以至于训练无法再有效进行。

图像：

3.RMSprop

简述：对Adagrad算法的一个改良，从AdaGrad以累计方式计算梯度变成指数衰减移动平均，并通过增加新参数“衰减率ß”，减小累计值对学习率的影响。当优化进行得越多，离得较远的数值对学习率的影响就越小。 “指数移动平均”也可以理解成一个移动窗口，只对窗口内的数据进行有效运算，而已经移出窗口的数据则对后续数据影响较小。

什么是指数衰减（加权）移动平均

指数加权移动均值（Exponentially Weighted Moving Average, EWMA）是一种计算有序序列的加权均值的统计学方法。该方法可以根据各个观测值在序列中的位置分配呈指数变化的权重，使得序列中越靠后的观测值对计算结果的影响越大；并且，它还可以通过参数调节权重的变化幅度。

可参考：Zenggyu的博客 - 指数加权移动均值的计算方法及代码实现

·优缺点：

①优点：RMSprop改善的是Adagrad随着更新深入学习率会越来越小的问题，由于累加的特性，Adagrad的学习率在更新一段时间以后就几乎为0几乎不动了，但RMSprop可以将学习率随时间变化的影响减小，从而继续推动学习率进行优化。

②缺点：该算法虽然改进了学习率可能变为0的地方，但对学习率的衰减相对较小，若找到最小值时学习率没有足够地降低，模型就可能在局部最小值附近波动或难以收敛，且该算法计算起来有些占内存。

图像：

4.Momentum

简述：Momentum 主要引入了基于梯度的移动指数加权平均的思想，当前的参数更新方向不仅与当前的梯度有关，也受历史的加权平均梯度影响。对于梯度指向相同方向的维度，动量会积累并增加，而对于梯度改变方向的维度，动量会减少更新。这也就使得收敛速度加快，同时又不至于摆动幅度太大。

因此Momentum算法就像将数据抛出一个小球，而参数的更新就像是加速度与速度之间的关系一样，小球落至图像的边缘再反弹回来，直至找到最小值。

·优缺点：

①优点：如下图所示，Momentum主要是对于SGD的优化，从图中可以看出，比起SGD，Momentum将之前积累的动量替代真正的梯度，从而优化了优化器迭代的速度的震荡的幅度。而且SGD很难从较陡的坡度走出局部最小值，而Momentum的“小球”在碰到陡坡时由于动量较大，故可以有力地冲出陡坡，从而实现走出局部最小值，达到全局最小值。

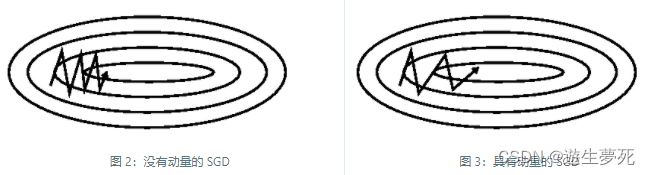
②缺点：Momentum算法使用指数加权平均来估计梯度的移动平均值，可能会导致过度调整，就像桌球一样，“小球”一直碰来碰去，但很难准确找到全局最小值。且如果在不同方向上的大幅度变化梯度，小球可能因为过早地加速，而在其他方向上减速，从而导致在参数空间中呈现椭圆形的路径，而不是直接收敛到最优点。

图像：

5.Adam（自适应矩估计）

简述：Adam也是“亚当”的意思，不知道是不是外国人的恶趣味。搜到了老师上课引用的论文。

翻译一下：

我们介绍了Adam这个算法。这是一种基于对随机目标函数进行梯度优化的一阶算法，其基础是对低阶矩的自适应估计。该方法易于实现，计算效率高，内存需求低，对梯度的对角重缩放不变，非常适用于数据和/或参数大的问题。该方法也适用于非平稳目标以及具有非常嘈杂和/或稀疏梯度的问题。超参数具有直观的解释，通常需要很少的调整。我们讨论了与Adam灵感来源的相关算法的一些联系。我们还分析了该算法的理论收敛性质，并在在线凸优化框架下提供了收敛速率的遗憾界，该界限与已知的最佳结果相当。实证结果表明，Adam在实践中表现良好，并与其他随机优化方法相比具有优势。最后，我们讨论了AdaMax，这是基于Adam的一种基于无穷范数的变体。

Adam算法是一种基于梯度的优化算法，同时融合了动量法和RMSprop的优点，引用了动量项和自适应学习率，并分别用超参数来表示这两个概念。在优化过程中，Adam通过指数加权平均来更新参数，使参数可以各自得到独特的更新，并引入了偏置修正机制，自动对两个超参数进行修正，从而在训练初期减轻偏置对它们的影响。正因如此，Adam算法拥有着极其强大的功能，正如下图所示，适用率非常高。

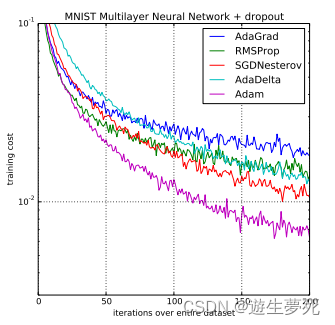
Adam 优化算法和其他优化算法在多层感知机模型中的对比​​​​​​​

如上算法所述，在确定了参数α、β1、β2 和随机目标函数 f(θ) 之后，我们需要初始化参数向量、一阶矩向量、二阶矩向量和时间步。然后当参数θ没有收敛时，循环迭代地更新各个部分。即时间步 t 加 1、更新目标函数在该时间步上对参数θ所求的梯度、更新偏差的一阶矩估计和二阶原始矩估计，再计算偏差修正的一阶矩估计和偏差修正的二阶矩估计，然后再用以上计算出来的值更新模型的参数θ。​​​​​​​

Adam算法的伪代码和代码讲解

优缺点：

①优点：从图就可以看出来，Adam可以很高效地找到最小值，且Adam可以用于解决稀疏数据和噪声问题，而且Adam和Insofar 基本是最好的全局选择，总之功能非常强大。

②缺点：Adam可能无法收敛到最优值。成也萧何败萧何，Adam因为指数移动平均数取得了成功，也是因此有可能收敛不到最优值，以下论文正是在谈论这一点。

不过对此，论文也给出了解决方法，有兴趣了解可以看看这篇论文：

https://arxiv.org/abs/1904.09237

Several recently proposed stochastic optimization methods that have been successfully used in training deep networks such as RMSProp, Adam, Adadelta, Nadam are based on using gradient updates scaled by square roots of exponential moving averages of squared past gradients. In many applications, e.g. learning with large output spaces, it has been empirically observed that these algorithms fail to converge to an optimal solution (or a critical point in nonconvex settings). We show that one cause for such failures is the exponential moving average used in the algorithms.

——《On the Convergence of Adam and Beyond》

图像：

·被优化函数  x2/20+y2（x、y）

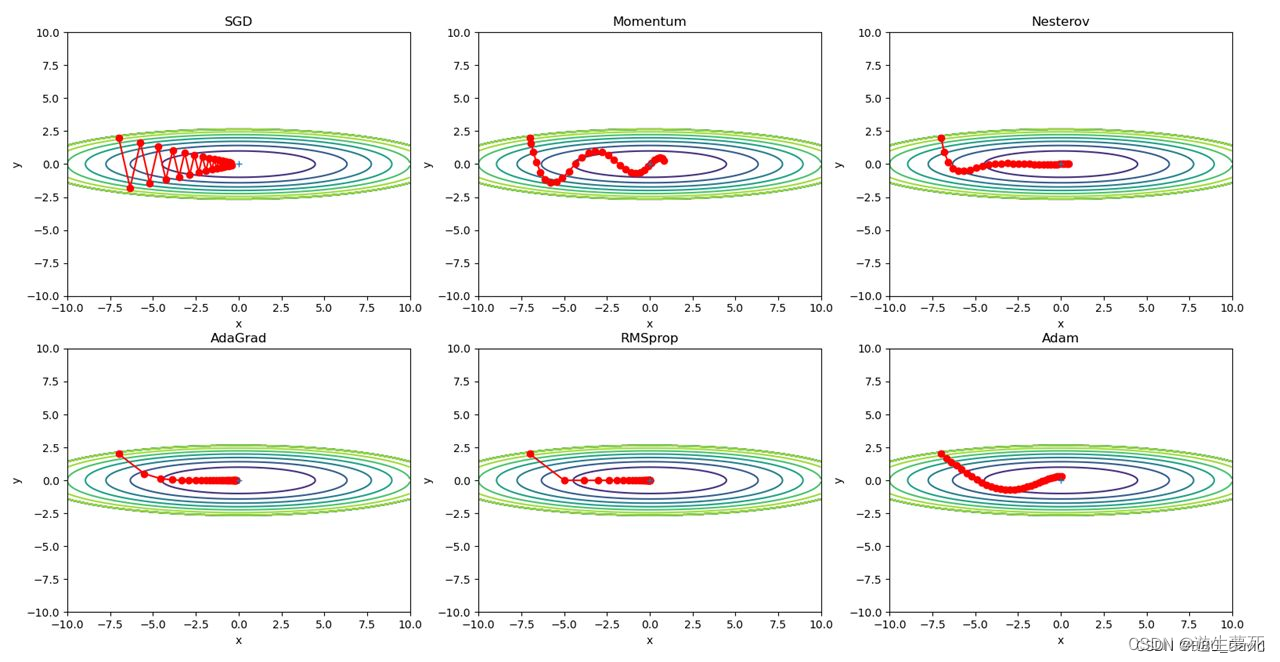
代码及实现

这次我们将实现不同算法在一个三维函数中寻找全局最小值的可视化，代码实现如下：

  1. # coding: utf-8
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4. from collections import OrderedDict
  5.  
  6.  
  7. class SGD:
  8.     """随机梯度下降法（Stochastic Gradient Descent）"""
  9.  
  10.     def __init__(self, lr=0.01):
  11.         self.lr = lr
  12.  
  13.     def update(self, params, grads):
  14.         for key in params.keys():
  15.             params[key] -= self.lr * grads[key]
  16.  
  17.  
  18. class Momentum:
  19.     """Momentum SGD"""
  20.  
  21.     def __init__(self, lr=0.01, momentum=0.9):
  22.         self.lr = lr
  23.         self.momentum = momentum
  24.         self.v = None
  25.  
  26.     def update(self, params, grads):
  27.         if self.v is None:
  28.             self.v = {}
  29.             for key, val in params.items():
  30.                 self.v[key] = np.zeros_like(val)
  31.  
  32.         for key in params.keys():
  33.             self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
  34.             params[key] += self.v[key]
  35.  
  36.  
  37. class Nesterov:
  38.     """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
  39.  
  40.     def __init__(self, lr=0.01, momentum=0.9):
  41.         self.lr = lr
  42.         self.momentum = momentum
  43.         self.v = None
  44.  
  45.     def update(self, params, grads):
  46.         if self.v is None:
  47.             self.v = {}
  48.             for key, val in params.items():
  49.                 self.v[key] = np.zeros_like(val)
  50.  
  51.         for key in params.keys():
  52.             self.v[key] *= self.momentum
  53.             self.v[key] -= self.lr * grads[key]
  54.             params[key] += self.momentum * self.momentum * self.v[key]
  55.             params[key] -= (1 + self.momentum) * self.lr * grads[key]
  56.  
  57. class RMSprop:
  58.     """RMSprop"""
  59.  
  60.     def __init__(self, lr=0.01, decay_rate=0.99):
  61.         self.lr = lr
  62.         self.decay_rate = decay_rate
  63.         self.h = None
  64.  
  65.     def update(self, params, grads):
  66.         if self.h is None:
  67.             self.h = {}
  68.             for key, val in params.items():
  69.                 self.h[key] = np.zeros_like(val)
  70.  
  71.         for key in params.keys():
  72.             self.h[key] *= self.decay_rate
  73.             self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
  74.             params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
  75.  
  76.  
  77. class AdaGrad:
  78.     """AdaGrad"""
  79.  
  80.     def __init__(self, lr=0.01):
  81.         self.lr = lr
  82.         self.h = None
  83.  
  84.     def update(self, params, grads):
  85.         if self.h is None:
  86.             self.h = {}
  87.             for key, val in params.items():
  88.                 self.h[key] = np.zeros_like(val)
  89.  
  90.         for key in params.keys():
  91.             self.h[key] += grads[key] * grads[key]
  92.             params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
  93.  
  94.  
  95. class RMSprop:
  96.     """RMSprop"""
  97.  
  98.     def __init__(self, lr=0.01, decay_rate=0.99):
  99.         self.lr = lr
  100.         self.decay_rate = decay_rate
  101.         self.h = None
  102.  
  103.     def update(self, params, grads):
  104.         if self.h is None:
  105.             self.h = {}
  106.             for key, val in params.items():
  107.                 self.h[key] = np.zeros_like(val)
  108.  
  109.         for key in params.keys():
  110.             self.h[key] *= self.decay_rate
  111.             self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
  112.             params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
  113.  
  114.  
  115. class Adam:
  116.     """Adam (http://arxiv.org/abs/1412.6980v8)"""
  117.  
  118.     def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
  119.         self.lr = lr
  120.         self.beta1 = beta1
  121.         self.beta2 = beta2
  122.         self.iter = 0
  123.         self.m = None
  124.         self.v = None
  125.  
  126.     def update(self, params, grads):
  127.         if self.m is None:
  128.             self.m, self.v = {}, {}
  129.             for key, val in params.items():
  130.                 self.m[key] = np.zeros_like(val)
  131.                 self.v[key] = np.zeros_like(val)
  132.  
  133.         self.iter += 1
  134.         lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
  135.  
  136.         for key in params.keys():
  137.             self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
  138.             self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
  139.  
  140.             params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
  141.  
  142.  
  143. def f(x, y):
  144.     return x ** 2 / 20.0 + y ** 2
  145.  
  146.  
  147. def df(x, y):
  148.     return x / 10.0, 2.0 * y
  149.  
  150.  
  151. init_pos = (-7.0, 2.0)
  152. params = {}
  153. params['x'], params['y'] = init_pos[0], init_pos[1]
  154. grads = {}
  155. grads['x'], grads['y'] = 0, 0
  156.  
  157. optimizers = OrderedDict()
  158. optimizers["SGD"] = SGD(lr=0.95)
  159. optimizers["Momentum"] = Momentum(lr=0.1)
  160. optimizers["Nesterov"] = Nesterov(lr=0.2)
  161. optimizers["AdaGrad"] = AdaGrad(lr=1.5)
  162. optimizers["RMSprop"] = RMSprop(lr=0.2)
  163. optimizers["Adam"] = Adam(lr=0.3)
  164.  
  165.  
  166. idx = 1
  167. fig = plt.figure(figsize=(12, 8))
  168. for key in optimizers:
  169.     optimizer = optimizers[key]
  170.     x_history = []
  171.     y_history = []
  172.     params['x'], params['y'] = init_pos[0], init_pos[1]
  173.  
  174.     for i in range(30):
  175.         x_history.append(params['x'])
  176.         y_history.append(params['y'])
  177.  
  178.         grads['x'], grads['y'] = df(params['x'], params['y'])
  179.         optimizer.update(params, grads)
  180.  
  181.     x = np.arange(-10, 10, 0.01)
  182.     y = np.arange(-5, 5, 0.01)
  183.  
  184.     X, Y = np.meshgrid(x, y)
  185.     Z = f(X, Y)
  186.     # for simple contour line
  187.     mask = Z > 7
  188.     Z[mask] = 0
  189.  
  190.     # plot
  191.     plt.subplot(2, 3, idx)
  192.     idx += 1
  193.     plt.plot(x_history, y_history, 'o-', color="red",markersize=3,zorder=1)
  194.     plt.contour(X, Y, Z,linewidths=0.8,zorder=0)  # 绘制等高线
  195.     plt.ylim(-10, 10)
  196.     plt.xlim(-10, 10)
  197.     plt.plot(0, 0, '+')
  198.     plt.title(key)
  199.     plt.xlabel("x")
  200.     plt.ylabel("y")
  201.  
  202. plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
  203. plt.show()

生成图像：

用教材代码跑出来的实验图像如下（图1），有点丑，而且调整了一下小球的大小还是挺丑，所以就去网上找了找有没有其他可以参考的代码，没有。

图1 用教材代码跑出来的模型

不过发现上一届学生作业中的代码画出的图非常好看，可惜只有四个图。寻门无果，我就只好硬着头皮在上一届学长学姐的代码基础上加上Nesterov和RMSprop的绘制代码了。好在过程挺顺利，最后画出来的图也比较符合想象，球比起上面的实例球小了一些，不过也能更直观地看到小球的轨迹，比较满意。

在这里给出一些以上代码用到的调整变量（？）还是参数，总之希望能便于看到这篇博文的人跑出更理想的图像：

·zorder=1/zorder=0：因为跑出的图像球轨迹被等高线遮住了，可以用zorder来调整二者的位置，将小球轨迹的zorder设置成1就可以让小球的轨迹跑在前面了。

·markersize=3：是小球的大小，我设置成了3，不过电脑不同设置的结果应该不同

·linewidths=0.8：等高线的宽度

·fig = plt.figure(figsize=(12, 8))：上届学长学姐的图只有四个图像，所以图像有点短，要想画出长长扁扁的图最简单的方法就是修改图像尺寸（难的我也不会）

·optimizers["Nesterov"] = Nesterov(lr=0.2)

·optimizers["RMSprop"] = RMSprop(lr=0.2)：本来是按教材给的那个代码设置的学习率，结果跑出图来这两个小球的轨迹龇牙咧嘴的，于是我又重新调整了一下学习率，大概看上去和老师举例的图像差不多了。不过教材给的学习率也并不是错的，只是修改后比较美观罢了。

·猜一猜

在找参考代码的时候，虽然没找到可参考代码，但意外地发现了一张图（图2），和上课演示的图一样有意思，而且也很直观地体现了不同算法面对全局最小值和局部最小值的区别：

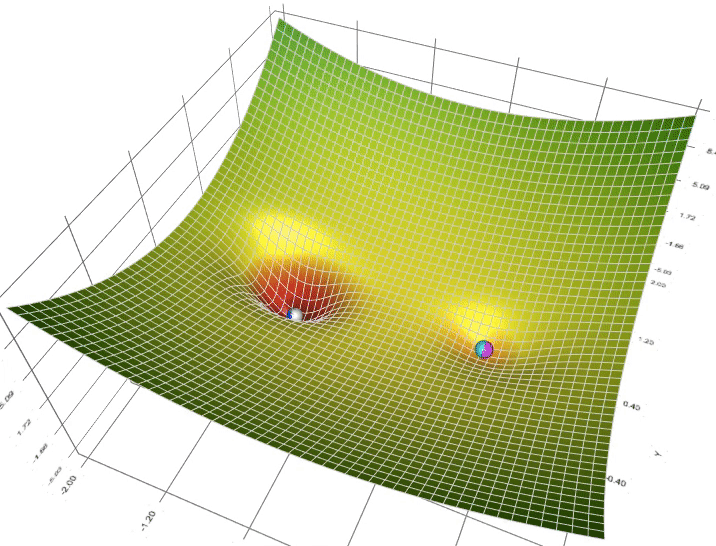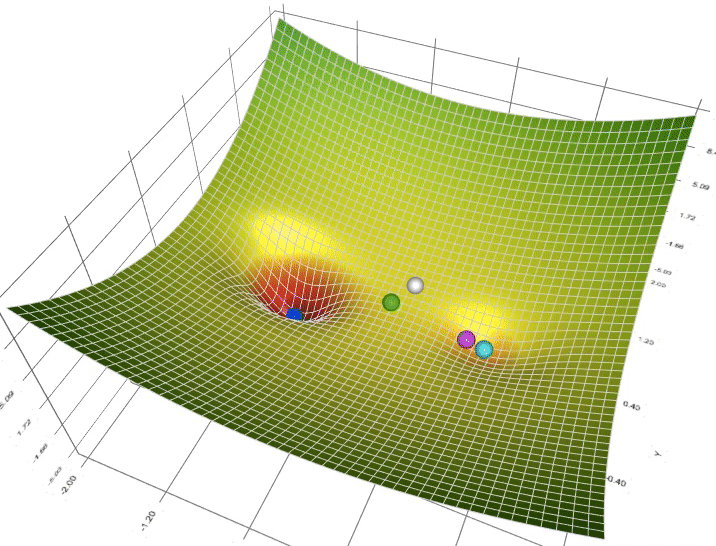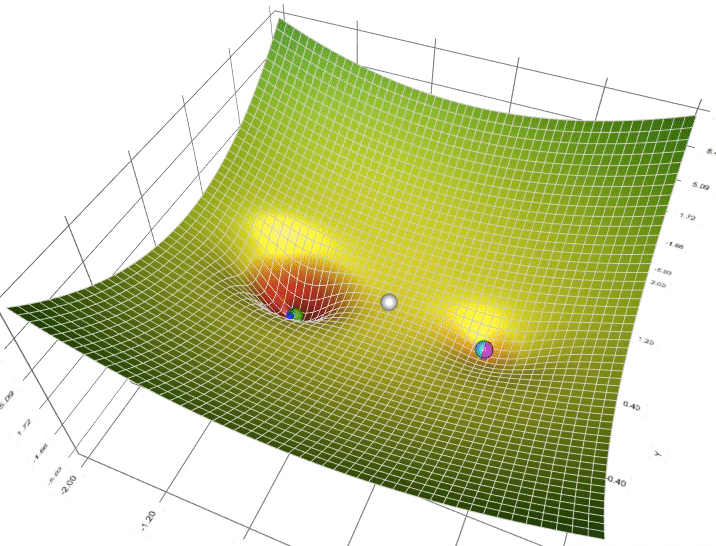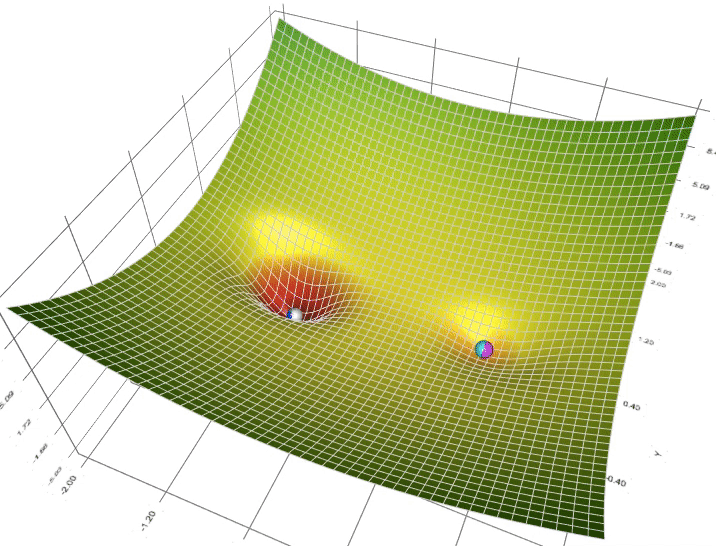
图二  不同算法的可视化

图二中并没有标明哪个颜色是哪个算法，那可以根据这个图上的小球先盲猜一下：

——“猜一猜”环节——

​​​​​​​
白色小球跑得最慢，稳稳的，所以猜应该是SGD；

天蓝色小球跑得最快，再坑里还转一转，但是跑错了，这个应该是动量最典型的代表Momentum；

绿色小球一开始跑得快，快到最小值就跑得慢悠悠地，怀疑是Adam；

深蓝色的小球冲得快，跑得对，可能是比Momentum更高一级的Nesterov；

粉色小球和白色一起速度比较慢，但比白色快一些，而且还跑错了，可能是Adagrad。

先不说答案，等到把下面的算法介绍完了再看看对不对，错误的原因在哪里。

SGD、Momentum、Adagrad、RMSprop、Adam在上面都已经说过，不再详谈。

6.Nesterov（牛顿动量算法）

简述：Nesterov算法本质上是对Momentum算法的改良，从上面的算法分析中可以看出，Momentum算法虽然是挺好，但就像上树的猪一样，不撞墙不知道回头。Nesterov算法就是在Momentum的基础上添加了参数修正的功能，在计算梯度时，通过下图中的公式，让之前的参数可以直接影响当前的参数，使得参数方向更新更为合理。

另一种解释是：“ Nesterov 与 Momentum 公式的区别在于, 前者不是在当前的位置上求梯度, 而是根据本来计划要走的那一步提前前进一步以后, 再在新的位置上求梯度, 然后对这个新求得的梯度进行 Momentum 梯度下降计算”

公式为什么要这样修改呢？引用一下其他博主的讲解：

它的直观含义就很明显了：如果这次的梯度比上次的梯度变大了，那么有理由相信它会继续变大下去，那我就把预计要增大的部分提前加进来；如果相比上次变小了，也是类似的情况。这样的解释听起来好像和原本的解释一样玄，但是读者可能已经发现了，这个多加上去的项不就是在近似目标函数的二阶导嘛！所以NAG本质上是多考虑了目标函数的二阶导信息，怪不得可以加速收敛了！其实所谓“往前看”的说法，在牛顿法这样的二阶方法中也是经常提到的，比喻起来是说“往前看”，数学本质上则是利用了目标函数的二阶导信息。

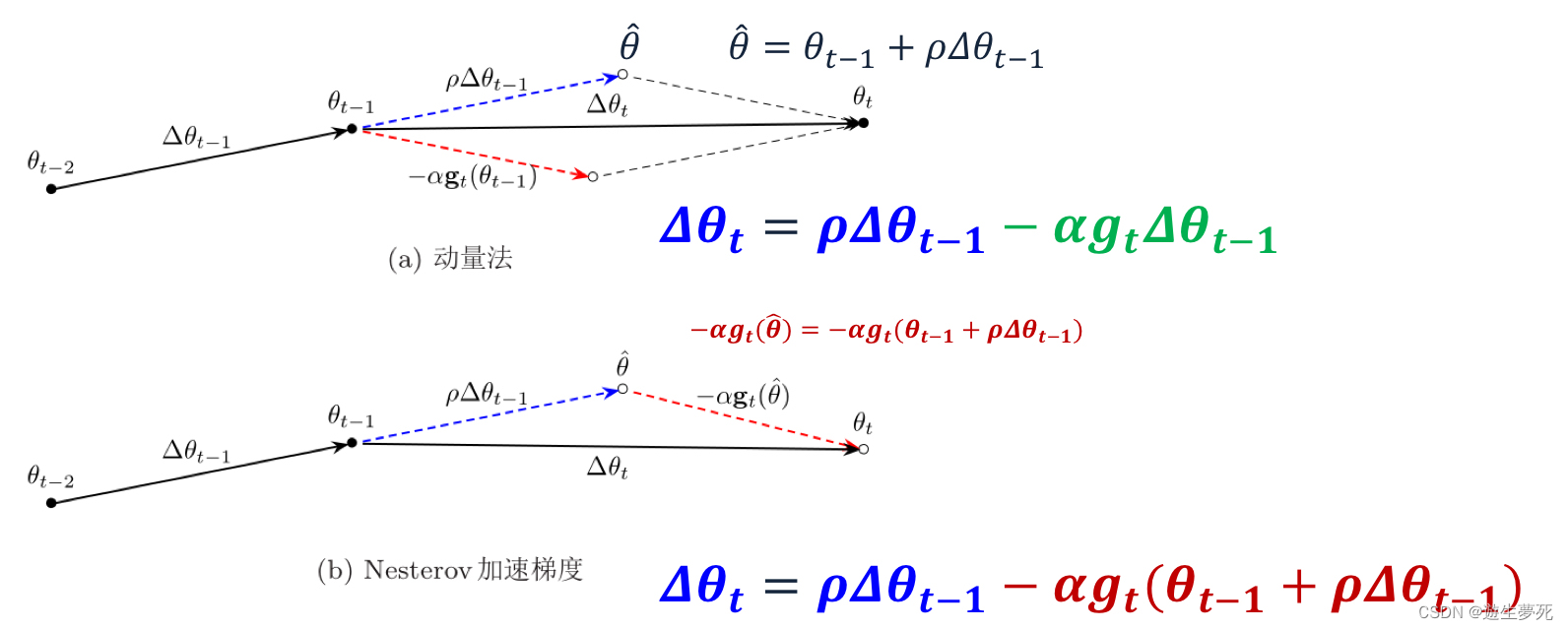
·优缺点：

①优点：优化算法之所以成立，就说明它比起它的前辈一定有进步。也就是说Nesterov算法与Momentum算法相比一定有自己的过人之处。比如Nesterov算法具有更好的收敛性，以及梯度更新更具有前瞻性，就像下棋一样，走一步看三步，走出的路线也更稳一些。

②缺点：增强了计算量，占用内存且运行时间更长，而且没有从根本上解决Momentum收敛率的问题。

· 解释不同轨迹的形成原因

·分析各个轨迹的原因

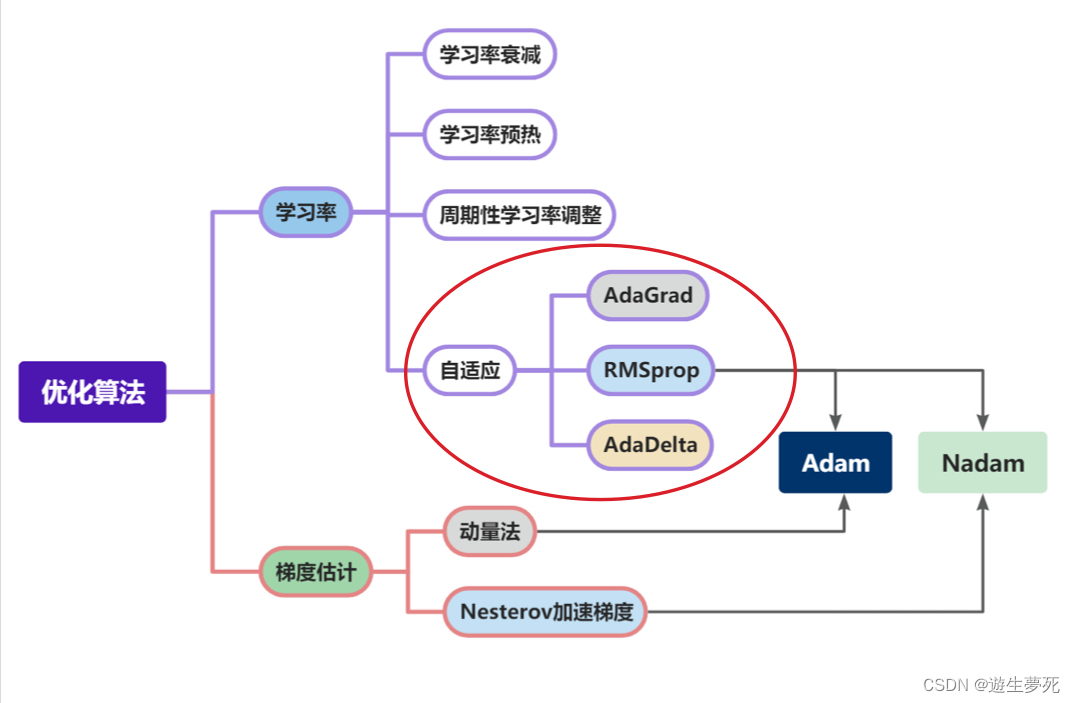
先简单总结一下各种算法的特点：

SGD——最基础的算法

Adagrad——在SGD上进行改良，通过累加的方法自动调整梯度，一开始跑得快，后面跑得慢

RMSprop——通过指数移动平均来改良Adagrad的累加计算梯度，以解决Adagrad中代码跑得太久，学习率逐渐降低为0的问题

Momentum——动量法，让优化的过程像小球跑，有机会跳出局部最小值

Nesterov——牛顿动量算法，对Momentum的优化，可以减缓Momentum的动荡

Adam——结合Momentum和RMSprop的优点，滚得快，方向也准。

复盘以后再来结合这两张图看，SGD是不断地再调整着方向，Adagrad和RMSprop就是找方向很准，直接奔着目标去了。Momentum、Nesterov都是蹦跶着找最小值的，但是Nesterov的震荡幅度要小一些；Adam虽然比较稳，但也还是有用了动量法的影子，轨迹是有一个小幅度波动的，而且三者都不是直接到达最小值，而是好像拥有“惯性”似的，超过最小值之后再绕回来。

·猜一猜谜底揭晓

再回来看这张图：

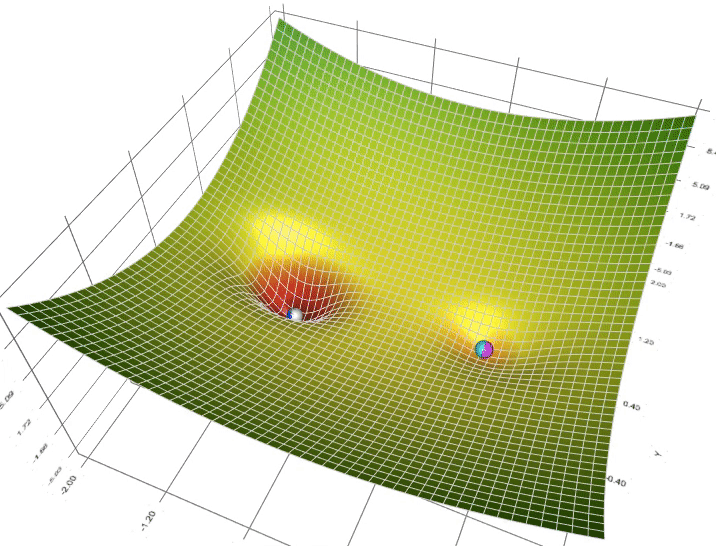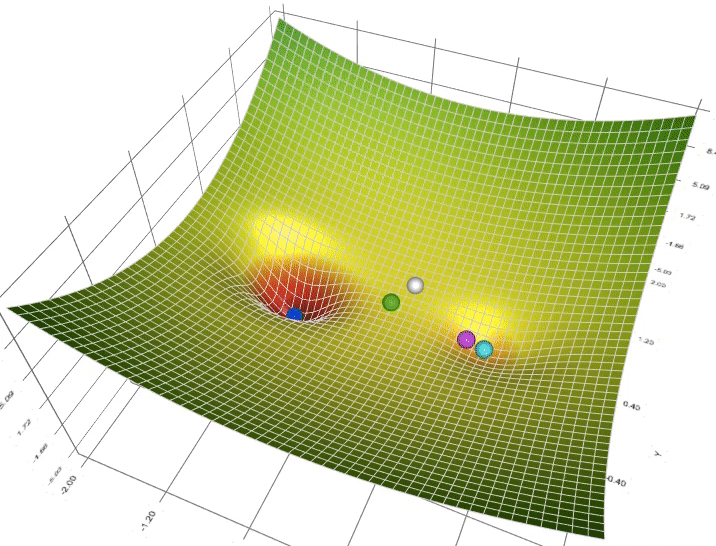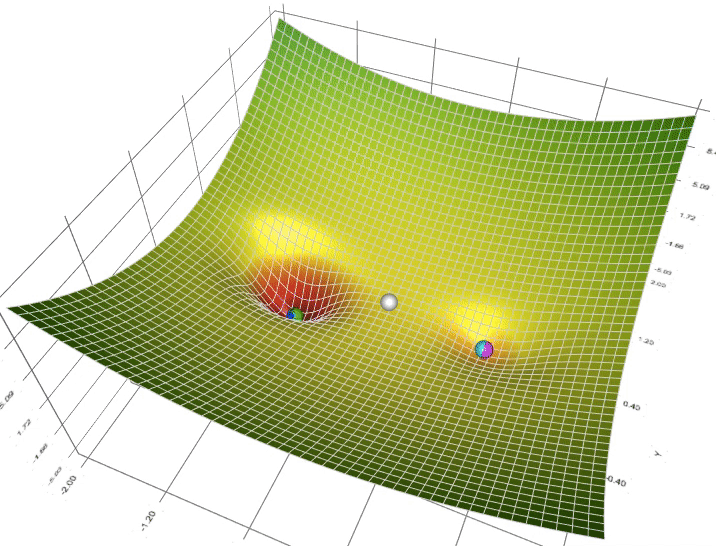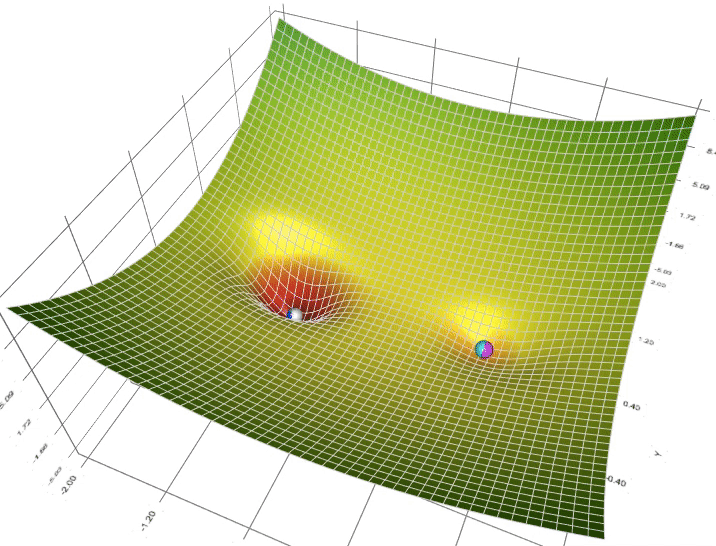
实际上，天蓝色的是SGD算法、粉红色的是Momentum算法、深蓝色的是Adam、白色的是Adagrad、绿色的是RMSprop。

错误分析：首先，是我对SGD算法刻板印象了，因为之前看了几个图，SGD都是跑得最慢的，所以我就先入为主以为白色的是SGD。

其次是Adam、Adagrad、RMSprop，其实把Adam猜成Nesterov也情有可原，当时我只想着Adam准确率高，但忽略了它也有着一定的动量成分，所以先入为主地把跑得快的划分进了Momentum和Nesterov。一步错步步错，所以剩下那几个全猜错了。

最后是Momentum，说实话我也想不明白为什么这个粉色的才是动量法，在原文看了看，大概是这样解释的：

让我们考虑两个极端情况来更好地理解这个衰减率（decay rate）参数。如果衰减率为0，那么它与原版梯度下降完全相同。如果衰减率是1，那么它就会像我们开始提到的无摩擦碗的类比一样，前后不断地摇摆; 你不会想要这样的结果。通常衰减率选择在0.8-0.9左右，它就像一个有一点摩擦的表面，所以它最终会减慢并停止。

解释一下也就是，粉色小球并不是我们理论上的动量小球，而是添加了类似摩擦力的衰减率，因此它会缓缓下降。

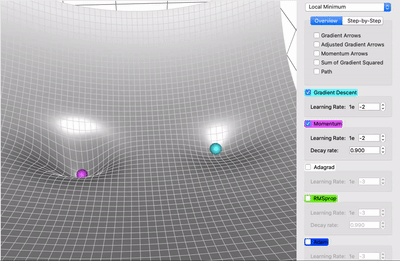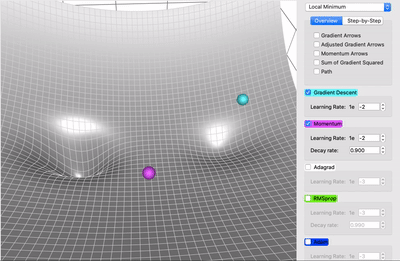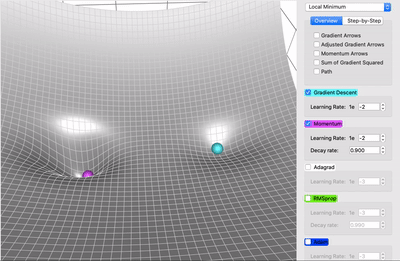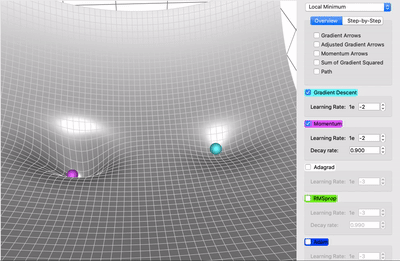
不同衰减率下动态小球的移动

·再训练，再讲解

经过总结与“猜一猜”之后，再把上课看过的图拿出来分析一下
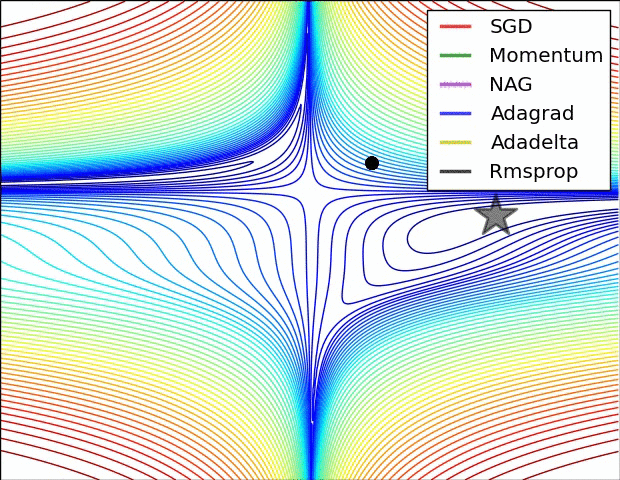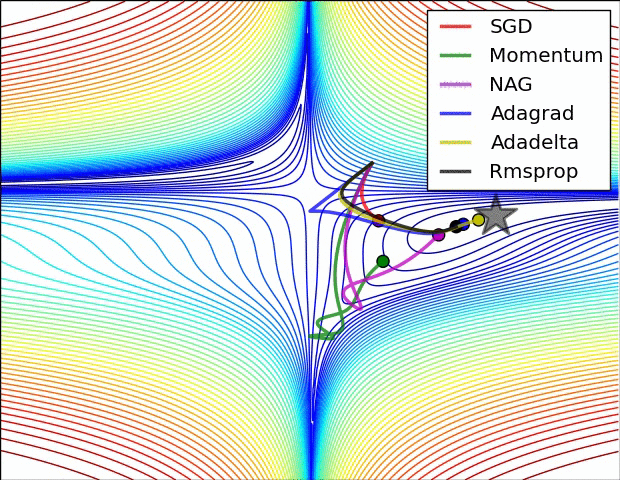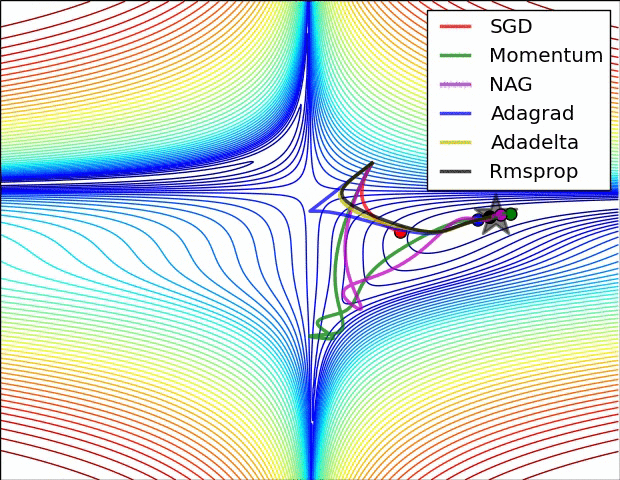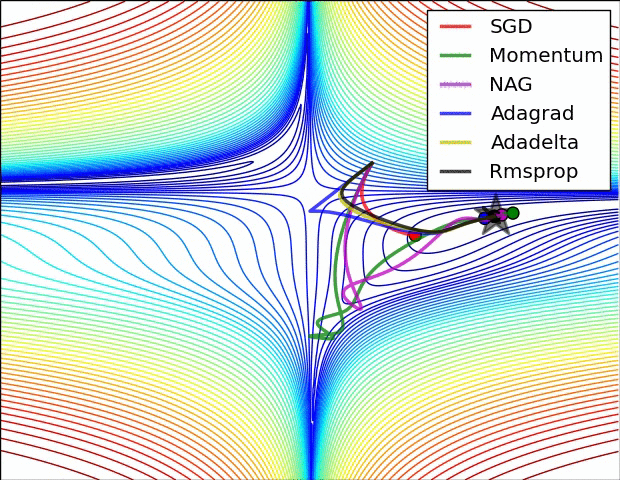
①

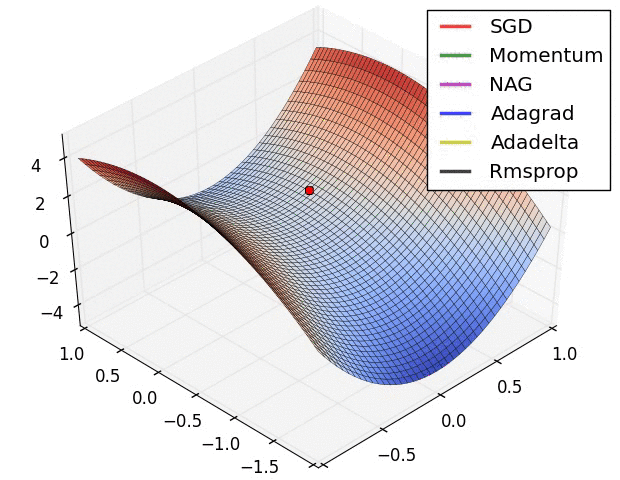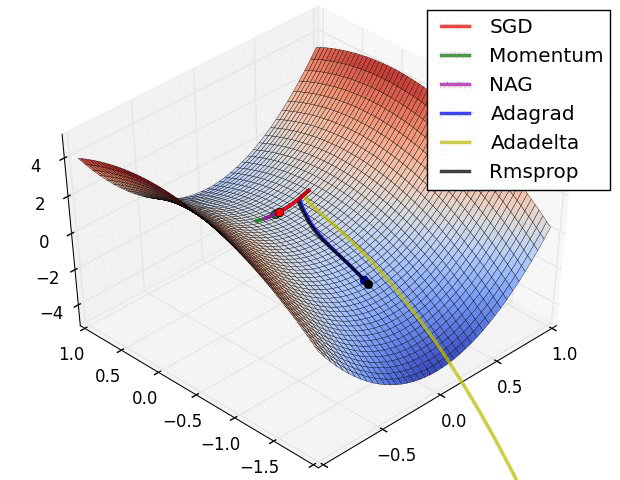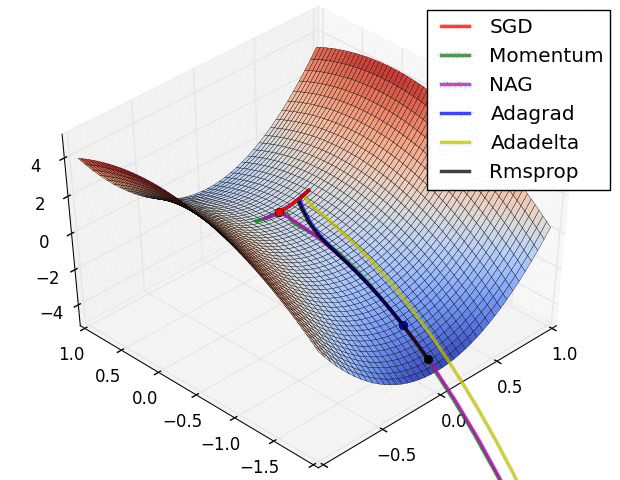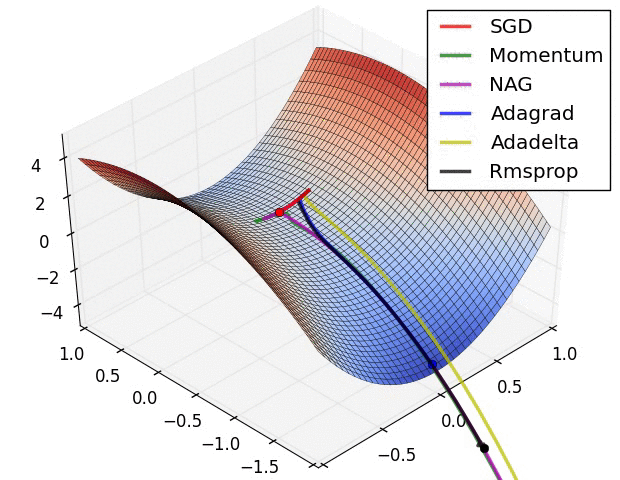
【·】图中一共有六个算法，其中Adadelta虽然没提到，不过和RMSprop、Adagrad也差不多，只是Adadelta不需要提前设置学习率，它通过指数衰减移动平均自己调整学习率，更智能一些。

再看上图，红色小球缓缓卡在局部最小值，所以应该是SGD；

绿色和紫色小球都有震荡波动，而后者震荡幅度小一些，所以紫色的是Nesterov，绿色的是Momentum。

这里没有Adam，如果有的话应该也会有一点波动幅度。

剩下三个都直接往全局最小值去了，这三个就是Adadelta、RMSprop、Adagrad自适应三巨头。深蓝色小球越跑越慢越跑越慢，所以它是那个渐渐学习率变成0的Adagrad。黄色小球一马当先，比起其它需要学习率缓冲的小球，它都不怎么拐弯，所以黄色的是Adadelta。剩下的则是RMSprop了。

②这个图和上一个图差不多，就不讲了。

小插曲：

在找资料的过程中，看到了不少有意思的东西。比如上面猜一猜的那个动图，请舍友一起猜猜看，小张同学居然五个猜对了四个，（不像我几乎全错）。这张动图相关的文章讲解了不同小球运行的原理，故小张看得非常过瘾，还要了链接。

另外，在寻找资料的过程中，我发现有个代码相关的网站上有nndl作业11，点开一看，原来是机器人把csdn里上届学长或者学姐的博客连名带文改都没改地搬过来了（NNDL 作业11：优化算法比较 - CodeAntenna）。顺着网站底下写的“原文链接”找到了上届的博客，问了问琳同学认不认识这个人，琳同学说不认识，并把博客链接拿去好好观摩了一番。

参考文献：

深度学习笔记（十）：SGD、Momentum、RMSprop、Adam优化算法解析_sgd和momentum-CSDN博客

​​​​​​​【代码】优化算法BGD、SGD、Momentum、Adam算法python实现_python sgd-CSDN博客

深度学习--优化器篇(超详细付代码测试流程包含：SGD，SGDM,NAG,Adagrad,RMSProp,Adam,Adadelta，Nadam等常用优化器) - 掘金

深度学习中的优化算法（Optimizer）理解与python实现 - 知乎

【23-24 秋学期】NNDL 作业12 优化算法2D可视化-CSDN博客

Zenggyu的博客 - 指数加权移动均值的计算方法及代码实现

https://zh.d2l.ai/chapter_optimization/adam.html

听说你了解深度学习最常用的学习算法：Adam优化算法？ | 机器之心

优化器(Optimizer)（SGD、Momentum、AdaGrad、RMSProp、Adam） | AI技术聚合

https://towardsdatascience.com/a-visual-explanation-of-gradient-descent-methods-momentum-adagrad-rmsprop-adam-f898b102325c

https://blog.51cto.com/stq054188/5835863

http://faculty.bicmr.pku.edu.cn/~wenzw/optbook/lect/20-lect-nesterov-ch.pdf

Nesterov Accelerated Gradient (NAG)优化算法详解_赏月斋的技术博客_51CTO博客

Ada_Nesterov动量法——一种具有自适应学习率的Nesterov动量法

各种优化方法整理总结 | 从零开始的BLOG

深度学习优化算法：从SGD到Nadam – X.YU

注：本文转载自blog.csdn.net的遊生夢死的文章"https://blog.csdn.net/qq_62591797/article/details/135191975"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！