机器学习笔记之优化算法——梯度下降法在凸函数上的收敛性
引言
本节将介绍梯度下降法在凸函数上的收敛性。
回顾:
收敛速度:次线性收敛
关于次线性收敛,分为两种判别类型:
R
\mathcal R
R-次线性收敛与
Q
\mathcal Q
Q-次线性收敛。而次线性收敛的特点是:随着迭代次数的增加,相邻迭代步骤产生的目标函数结果
f
(
x
k
)
,
f
(
x
k
+
1
)
f(x_k),f(x_{k+1})
f(xk),f(xk+1),其差异性几乎完全相同:
lim
k
⇒
∞
∣
∣
x
k
+
1
−
x
∗
∣
∣
∣
∣
x
k
−
x
∗
∣
∣
=
1
\mathop{\lim}\limits_{k \Rightarrow \infty}\frac{||x_{k+1} - x^*||}{||x_k - x^*||} = 1
k⇒∞lim∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣=1
例如:如果数值解
x
k
x_k
xk的目标函数结果
f
(
x
k
)
f(x_k)
f(xk)与目标函数最优解
f
∗
f^*
f∗之间的差异性
∣
∣
f
(
x
k
)
−
f
∗
∣
∣
||f(x_k) - f^*||
∣∣f(xk)−f∗∣∣与迭代次数
k
k
k存在如下函数关系
G
(
k
)
\mathcal G(k)
G(k):
∣
∣
f
(
x
k
)
−
f
∗
∣
∣
≤
G
(
k
)
=
1
k
||f(x_k) - f^*|| \leq \mathcal G(k) = \frac{1}{k}
∣∣f(xk)−f∗∣∣≤G(k)=k1
当
k
k
k充分大时,
f
(
x
k
)
,
f
(
x
k
+
1
)
f(x_k),f(x_{k+1})
f(xk),f(xk+1)与
f
∗
f^*
f∗之间差异性的比值表示如下:
lim
k
⇒
∞
∣
∣
f
(
x
k
+
1
)
−
f
∗
∣
∣
∣
∣
f
(
x
k
)
−
f
∗
∣
∣
=
lim
k
⇒
∞
k
k
+
1
=
1
\mathop{\lim}\limits_{k \Rightarrow \infty} \frac{||f(x_{k+1}) - f^*||}{||f(x_k) - f^*||} = \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{k}{k+1} = 1
k⇒∞lim∣∣f(xk)−f∗∣∣∣∣f(xk+1)−f∗∣∣=k⇒∞limk+1k=1
也就是说:虽然随着
k
k
k的增加,
f
(
x
k
)
f(x_k)
f(xk)在减小;但相邻迭代结果
f
(
x
k
)
,
f
(
x
k
+
1
)
f(x_k),f(x_{k+1})
f(xk),f(xk+1)之间的差异性几乎可以忽略不计。那么称这种收敛速度为次线性收敛。
准确的说,是
⇒
0
\Rightarrow 0
⇒0的次线性收敛:
lim
k
⇒
∞
{
f
(
x
k
)
}
⇒
lim
k
⇒
∞
G
(
k
)
=
0
\mathop{\lim}\limits_{k \Rightarrow \infty} \{f(x_k)\} \Rightarrow \mathop{\lim}\limits_{k \Rightarrow \infty} \mathcal G(k) = 0
k⇒∞lim{f(xk)}⇒k⇒∞limG(k)=0
二次上界引理
关于二次上界引理的描述表示如下:如果函数
f
(
⋅
)
f(\cdot)
f(⋅)可微,并对应梯度函数
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)满足利普希兹连续,则函数
f
(
⋅
)
f(\cdot)
f(⋅)存在二次上界。即:
∀
x
,
y
∈
R
n
⇒
f
(
y
)
≤
f
(
x
)
+
[
∇
f
(
x
)
]
T
(
y
−
x
)
+
L
2
∣
∣
y
−
x
∣
∣
2
\forall x,y \in \mathbb R^n \Rightarrow f(y) \leq f(x) + [\nabla f(x)]^T (y - x) + \frac{\mathcal L}{2}||y - x||^2
∀x,y∈Rn⇒f(y)≤f(x)+[∇f(x)]T(y−x)+2L∣∣y−x∣∣2
而二次上界引理的作用是:可以通过该引理,得到最优步长上界的最小值:
- 假设
x
x
x固定,令
ϕ
(
y
)
=
f
(
x
)
+
[
∇
f
(
x
)
]
T
(
y
−
x
)
+
L
2
∣
∣
y
−
x
∣
∣
2
ϕ(y)=f(x)+[∇f(x)]T(y−x)+L2||y−x||2ϕ(y)=f(x)+[∇f(x)]T(y−x)+2L∣∣y−x∣∣2,通过选择合适的 y m i n y_{min} ymin,使 ϕ ( y ) \phi(y) ϕ(y)达到最小值:
ϕ(y)=f(x)+[∇f(x)]T(y−x)+L2||y−x||2
y m i n = arg min y ∈ R n ϕ ( y ) y_{min} = \mathop{\arg\min}\limits_{y \in \mathbb R^n} \phi(y) ymin=y∈Rnargminϕ(y) - 令
∇
ϕ
(
y
)
≜
0
\nabla \phi(y) \triangleq 0
∇ϕ(y)≜0,有:
y m i n = x + 1 L ⋅ [ − ∇ f ( x ) ] y_{min} = x + \frac{1}{\mathcal L} \cdot [- \nabla f(x)] ymin=x+L1⋅[−∇f(x)] - 其中
−
∇
f
(
x
)
- \nabla f(x)
−∇f(x)即
P
k
\mathcal P_k
Pk,也就是最速下降方向;而
1
L
1LL1则是最优步长的上确界:
1L
f ( y ) ≤ ϕ ( y m i n ) = min y ∈ R n ϕ ( y ) f(y) \leq \phi(y_{min}) = \mathop{\min}\limits_{y \in \mathbb R^n} \phi(y) f(y)≤ϕ(ymin)=y∈Rnminϕ(y)
也就是说:- 在没有二次上界引理的约束下,步长 α k \alpha_k αk的选择在其定义域内没有约束: ( 0 , + ∞ ) (0, +\infty) (0,+∞);
- 经过二次上界引理的约束后,步长
α
k
\alpha_k
αk的选择从原始的
(
0
,
+
∞
)
(0,+\infty)
(0,+∞)约束至
(
0
,
1
L
]
(0,1L](0,L1]。
延伸:关于区间
(
0
,
1
L
]
(0,1L]
吐槽:实际上用这张图是不太合理的,因为下面的图对应的
f
(
⋅
)
f(\cdot)
f(⋅)更加复杂,二次上界约束的范围仅仅在下面
α
\alpha
α轴的绿色实线部分,但很明显,在该函数中,存在更优质的
α
\alpha
α结果。
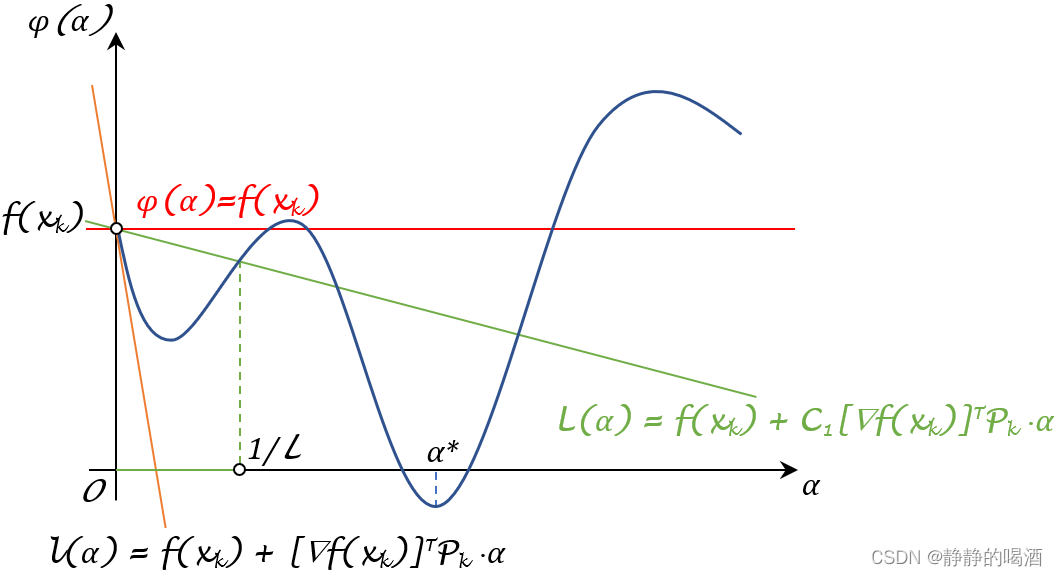
梯度下降法在凸函数上的收敛性
收敛性定理介绍
梯度下降法在凸函数上的收敛性定理表示如下:
- 条件:
- 函数 f ( ⋅ ) f(\cdot) f(⋅)向下有界,在定义域内可微,并且 f ( ⋅ ) f(\cdot) f(⋅)是凸函数;
- 关于 f ( ⋅ ) f(\cdot) f(⋅)的梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足利普希兹连续;
- 梯度下降法迭代过程中步长
α
k
(
k
=
1
,
2
,
3
,
⋯
)
\alpha_k(k=1,2,3,\cdots)
αk(k=1,2,3,⋯)有明确的约束范围:
α
k
∈
(
0
,
1
L
]
αk∈(0,1L]αk∈(0,L1];
- 结论:数值解序列
{
x
k
}
k
=
0
∞
\{x_{k}\}_{k=0}^{\infty}
{xk}k=0∞对应的目标函数结果
{
f
(
x
k
)
}
k
=
0
∞
\{f(x_k)\}_{k=0}^{\infty}
{f(xk)}k=0∞以
O
(
1
k
)
O(1k)O(k1)收敛于目标函数最优解 f ∗ f^* f∗。
其中O ( 1 k ) O(1k)O(k1)表示以G ( k ) = C ⋅ 1 k G(k)=C⋅1kG(k)=C⋅k1的次线性收敛级别的收敛速度(C \mathcal C C为常数)。
证明过程
根据二次上界引理,依然将
x
x
x设为上一次迭代的数值解
x
i
−
1
x_{i-1}
xi−1,对应的
y
y
y为当前迭代步骤的数值解
x
i
x_i
xi。由于是梯度下降法,因而在线搜索方法的基础上,将方向
P
i
\mathcal P_i
Pi表示为最速下降方向
∇
f
(
x
i
−
1
)
\nabla f(x_{i-1})
∇f(xi−1)步长依然使用步长变量
α
\alpha
α进行表示:
y
−
x
=
x
i
−
x
i
−
1
=
−
∇
f
(
x
i
−
1
)
⋅
α
y - x = x_i - x_{i - 1} = -\nabla f(x_{i-1}) \cdot \alpha
y−x=xi−xi−1=−∇f(xi−1)⋅α
将二次上界不等式进行相应替换:
将上式代入~
f
(
x
i
)
≤
f
(
x
i
−
1
)
+
[
∇
f
(
x
i
−
1
)
]
T
[
−
∇
f
(
x
i
−
1
)
⋅
α
]
+
L
2
∣
∣
−
∇
f
(
x
i
−
1
)
⋅
α
∣
∣
2
f(x_i) \leq f(x_{i-1}) + [\nabla f(x_{i-1})]^T [-\nabla f(x_{i-1}) \cdot \alpha] + \frac{\mathcal L}{2} ||-\nabla f(x_{i-1}) \cdot \alpha||^2
f(xi)≤f(xi−1)+[∇f(xi−1)]T[−∇f(xi−1)⋅α]+2L∣∣−∇f(xi−1)⋅α∣∣2
观察不等式右侧,可以继续化简:
将内积写作∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||^2 ∣∣⋅∣∣2的形式。-
∣
∣
−
∇
f
(
x
i
−
1
)
⋅
α
∣
∣
2
=
∣
∣
∇
f
(
x
i
−
1
)
⋅
α
∣
∣
2
||- \nabla f(x_{i-1}) \cdot \alpha||^2 = ||\nabla f(x_{i-1}) \cdot \alpha||^2
∣∣−∇f(xi−1)⋅α∣∣2=∣∣∇f(xi−1)⋅α∣∣2
,这里消掉一个负号; 由于α ∈ ( 0 , 1 L ] α∈(0,1L]α∈(0,L1],是一个标量,直接将其提到范数外侧。
I r i g h t = f ( x i − 1 ) − α ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 + L 2 ⋅ α 2 ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 \mathcal I_{right} = f(x_{i-1}) - \alpha \cdot ||\nabla f(x_{i-1})||^2 + \frac{\mathcal L}{2} \cdot \alpha^2 \cdot ||\nabla f(x_{i-1})||^2 Iright=f(xi−1)−α⋅∣∣∇f(xi−1)∣∣2+2L⋅α2⋅∣∣∇f(xi−1)∣∣2
由
α
≤
1
L
α≤1L
消掉分母中的
α
\alpha
α,并于前面的项结合。
I
r
i
g
h
t
≤
f
(
x
i
−
1
)
−
α
⋅
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
+
1
2
α
⋅
α
2
⋅
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
=
f
(
x
i
−
1
)
−
α
2
⋅
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
Iright≤f(xi−1)−α⋅||∇f(xi−1)||2+12α⋅α2⋅||∇f(xi−1)||2=f(xi−1)−α2⋅||∇f(xi−1)||2
基于梯度下降法,使用二次上界引理,可以得到
f
(
x
i
−
1
)
f(x_{i-1})
f(xi−1)与
f
(
x
i
)
f(x_i)
f(xi)之间存在如下关联关系:
f
(
x
i
)
≤
f
(
x
i
−
1
)
−
α
2
⋅
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
i
=
1
,
2
,
3
,
⋯
f(x_i) \leq f(x_{i-1}) - \frac{\alpha}{2} \cdot ||\nabla f(x_{i-1})||^2\quad i=1,2,3,\cdots
f(xi)≤f(xi−1)−2α⋅∣∣∇f(xi−1)∣∣2i=1,2,3,⋯
根据凸函数的性质,必然有:函数
f
(
⋅
)
f(\cdot)
f(⋅)任一位置的切线,
f
(
⋅
)
f(\cdot)
f(⋅)均在该切线上方。见下图:
由于条件:
f
(
⋅
)
f(\cdot)
f(⋅)向下有界,因此,该函数必然’开口向上‘。
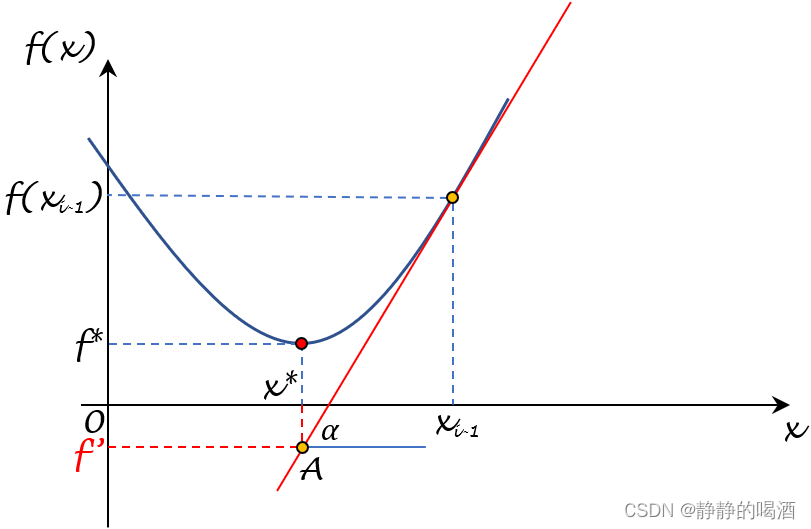
其中红色点
(
x
∗
,
f
∗
)
(x^*,f^*)
(x∗,f∗)表示最优点,以上一次迭代产生的
x
i
−
1
x_{i-1}
xi−1为切点做一条切线,必然有
x
∗
x^*
x∗在该切线函数上的函数值
f
′
≤
f
∗
f' \leq f^*
f′≤f∗。
f
′
f'
f′表示如下:
f
′
=
f
(
x
i
−
1
)
−
[
∇
f
(
x
i
−
1
)
]
T
(
x
i
−
1
−
x
∗
)
≤
f
∗
f' = f(x_{i-1}) - [\nabla f(x_{i-1})]^T (x_{i-1} - x^*) \leq f^*
f′=f(xi−1)−[∇f(xi−1)]T(xi−1−x∗)≤f∗
移项,从而有:
f
(
x
i
−
1
)
≤
f
∗
+
[
∇
f
(
x
i
−
1
)
]
T
(
x
i
−
1
−
x
∗
)
f(x_{i-1}) \leq f^* + [\nabla f(x_{i-1})]^T (x_{i-1} - x^*)
f(xi−1)≤f∗+[∇f(xi−1)]T(xi−1−x∗)
将上式代入,有:
I
r
i
g
h
t
≤
f
∗
+
[
∇
f
(
x
i
−
1
)
]
T
(
x
i
−
1
−
x
∗
)
⏟
替换
f
(
x
i
−
1
)
−
α
2
⋅
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
\mathcal I_{right} \leq \underbrace{f^* + [\nabla f(x_{i-1})]^T (x_{i-1} - x^*)}_{替换f(x_{i-1})}- \frac{\alpha}{2} \cdot ||\nabla f(x_{i-1})||^2
Iright≤替换f(xi−1)
f∗+[∇f(xi−1)]T(xi−1−x∗)−2α⋅∣∣∇f(xi−1)∣∣2
为了凑平方项,将上式调整至如下形式:
将
−
α
2
−α2凑出
α
2
\alpha^2
α2,其他项跟随变化。
I
r
i
g
h
t
≤
−
1
2
α
{
α
2
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
−
2
α
⋅
[
∇
f
(
x
i
−
1
)
]
T
(
x
i
−
1
−
x
∗
)
}
\mathcal I_{right} \leq -\frac{1}{2 \alpha} \left\{\alpha^2 ||\nabla f(x_{i-1})||^2 - 2\alpha \cdot [\nabla f(x_{i-1})]^T(x_{i-1} - x^*)\right\}
Iright≤−2α1{α2∣∣∇f(xi−1)∣∣2−2α⋅[∇f(xi−1)]T(xi−1−x∗)}
对大括号内的项进行配方:
I
r
i
g
h
t
≤
f
∗
−
1
2
α
{
α
2
∣
∣
∇
f
(
x
i
−
1
)
∣
∣
2
−
2
α
⋅
[
∇
f
(
x
i
−
1
)
]
T
(
x
i
−
1
−
x
∗
)
+
∣
∣
x
i
−
1
−
x
∗
∣
∣
2
⏟
平方项
−
∣
∣
x
i
−
1
−
x
∗
∣
∣
2
}
=
f
∗
−
1
2
α
[
∣
∣
α
⋅
∇
f
(
x
i
−
1
)
−
(
x
i
−
1
−
x
∗
)
∣
∣
2
−
∣
∣
x
i
−
1
−
x
∗
∣
∣
2
]
Iright≤f∗−12α{α2||∇f(xi−1)||2−2α⋅[∇f(xi−1)]T(xi−1−x∗)+||xi−1−x∗||2⏟平方项−||xi−1−x∗||2}=f∗−12α[||α⋅∇f(xi−1)−(xi−1−x∗)||2−||xi−1−x∗||2]
观察中括号内第一项:
∣
∣
α
⋅
∇
f
(
x
i
−
1
)
−
(
x
i
−
1
−
x
∗
)
∣
∣
2
||\alpha \cdot \nabla f(x_{i-1}) - (x_{i-1} - x^*)||^2
∣∣α⋅∇f(xi−1)−(xi−1−x∗)∣∣2,由于是范数的平方项,因而在范数内部添加一个负号不会影响其值的变化:
∣
∣
α
⋅
∇
f
(
x
i
−
1
)
−
(
x
i
−
1
−
x
∗
)
∣
∣
2
=
∣
∣
x
i
−
1
−
α
⋅
∇
f
(
x
i
−
1
)
−
x
∗
∣
∣
2
||\alpha \cdot \nabla f(x_{i-1}) - (x_{i-1} - x^*)||^2 = ||x_{i-1} - \alpha \cdot \nabla f(x_{i-1}) - x^*||^2
∣∣α⋅∇f(xi−1)−(xi−1−x∗)∣∣2=∣∣xi−1−α⋅∇f(xi−1)−x∗∣∣2
从迭代角度观察:
x
i
−
1
−
α
⋅
∇
f
(
x
i
−
1
)
=
x
i
x_{i-1} - \alpha \cdot \nabla f(x_{i-1}) = x_{i}
xi−1−α⋅∇f(xi−1)=xi,从而上式可继续化简为:
提一个负号,调换一下位置。
{
∣
∣
α
⋅
∇
f
(
x
i
−
1
)
−
(
x
i
−
1
−
x
∗
)
∣
∣
2
=
∣
∣
x
i
−
x
∗
∣
∣
2
I
r
i
g
h
t
≤
f
∗
−
1
2
α
[
∣
∣
x
i
−
x
∗
∣
∣
2
−
∣
∣
x
i
−
1
−
x
∗
∣
∣
2
]
=
f
∗
+
1
2
α
[
∣
∣
x
i
−
1
−
x
∗
∣
∣
2
−
∣
∣
x
i
−
x
∗
∣
∣
2
]
{||α⋅∇f(xi−1)−(xi−1−x∗)||2=||xi−x∗||2Iright≤f∗−12α[||xi−x∗||2−||xi−1−x∗||2]=f∗+12α[||xi−1−x∗||2−||xi−x∗||2]
至此,可以得到如下不等式结果:
f
(
x
i
)
−
f
∗
≤
1
2
α
(
∣
∣
x
i
−
1
−
x
∗
∣
∣
2
−
∣
∣
x
i
−
x
∗
∣
∣
2
)
f(x_i) - f^* \leq \frac{1}{2\alpha}(||x_{i-1} - x^*||^2 - ||x_i - x^*||^2)
f(xi)−f∗≤2α1(∣∣xi−1−x∗∣∣2−∣∣xi−x∗∣∣2)
观察:不等式左侧描述的意义是:当前迭代步骤的目标函数结果
f
(
x
i
)
f(x_i)
f(xi)与最优解
f
∗
f^*
f∗之间的偏差。从初始化数值解
x
0
x_0
x0开始,我们会得到一系列的不等式结果:
{
f
(
x
1
)
−
f
∗
≤
1
2
α
(
∣
∣
x
0
−
x
∗
∣
∣
2
−
∣
∣
x
1
−
x
∗
∣
∣
2
)
f
(
x
2
)
−
f
∗
≤
1
2
α
(
∣
∣
x
1
−
x
∗
∣
∣
2
−
∣
∣
x
2
−
x
∗
∣
∣
2
)
⋮
f
(
x
k
)
−
f
∗
≤
1
2
α
(
∣
∣
x
k
−
1
−
x
∗
∣
∣
2
−
∣
∣
x
k
−
x
∗
∣
∣
2
)
{f(x1)−f∗≤12α(||x0−x∗||2−||x1−x∗||2)f(x2)−f∗≤12α(||x1−x∗||2−||x2−x∗||2)⋮f(xk)−f∗≤12α(||xk−1−x∗||2−||xk−x∗||2)
将这些不等式对应位置相加,有:
等式右侧的中间项都被消掉了~因为∣ ∣ x k − x ∗ ∣ ∣ 2 ≥ 0 ||x_k - x^*||^2 \geq 0 ∣∣xk−x∗∣∣2≥0恒成立,从而消掉含变量的项。
∑ i = 1 k [ f ( x i ) − f ∗ ] ≤ 1 2 α ( ∣ ∣ ∣ x 0 − x ∗ ∣ ∣ 2 − ∣ ∣ x k − x ∗ ∣ ∣ 2 ) ≤ 1 2 α ∣ ∣ x 0 − x ∗ ∣ ∣ 2 \sum_{i=1}^k [f(x_i) - f^*] \leq \frac{1}{2\alpha}(|||x_0 - x^*||^2 - ||x_k - x^*||^2) \leq \frac{1}{2 \alpha} ||x_0 - x^*||^2 i=1∑k[f(xi)−f∗]≤2α1(∣∣∣x0−x∗∣∣2−∣∣xk−x∗∣∣2)≤2α1∣∣x0−x∗∣∣2
关于我们要证的 ∣ ∣ f ( x k ) − f ∗ ∣ ∣ ||f(x_k) - f^*|| ∣∣f(xk)−f∗∣∣,可以表示为如下形式:
由于优化问题的收敛性,必然有: f ( x k ) ≤ f ( x k − 1 ) ≤ ⋯ ≤ f ( x 1 ) f(x_{k}) \leq f(x_{k-1})\leq \cdots\leq f(x_1) f(xk)≤f(xk−1)≤⋯≤f(x1),从而每一项:∣ ∣ f ( x k ) − f ∗ ∣ ∣ ≤ ∣ ∣ f ( x k − 1 ) − f ∗ ∣ ∣ ≤ ⋯ ≤ ∣ ∣ f ( x 1 ) − f ∗ ∣ ∣ ||f(x_k) - f^*|| \leq ||f(x_{k-1}) - f^*|| \leq \cdots \leq ||f(x_1) - f^*|| ∣∣f(xk)−f∗∣∣≤∣∣f(xk−1)−f∗∣∣≤⋯≤∣∣f(x1)−f∗∣∣,从而有:∑ i = 1 k [ f ( x k ) − f ∗ ] ≤ ∑ i = 1 k [ f ( x i ) − f ∗ ] k∑i=1[f(xk)−f∗]≤k∑i=1[f(xi)−f∗]i=1∑k[f(xk)−f∗]≤i=1∑k[f(xi)−f∗]。将上式结果带入~
f ( x k ) − f ∗ = 1 k ∑ i = 1 k [ f ( x k ) − f ∗ ] ≤ 1 k ∑ i = 1 k [ f ( x i ) − f ∗ ] ≤ 1 k [ 1 2 α ∣ ∣ x 0 − x ∗ ∣ ∣ 2 ] f(x_k) - f^* = \frac{1}{k} \sum_{i=1}^{k}[f(x_k) - f^*] \leq \frac{1}{k} \sum_{i=1}^{k}[f(x_i) - f^*] \leq \frac{1}{k} \left[\frac{1}{2\alpha}||x_0 - x^*||^2\right] f(xk)−f∗=k1i=1∑k[f(xk)−f∗]≤k1i=1∑k[f(xi)−f∗]≤k1[2α1∣∣x0−x∗∣∣2]
观察:
[
1
2
α
∣
∣
x
0
−
x
∗
∣
∣
2
]
[12α||x0−x∗||2]
f
(
x
k
)
−
f
∗
≤
1
k
⋅
C
f(x_k) - f^* \leq \frac{1}{k} \cdot \mathcal C
f(xk)−f∗≤k1⋅C
我们可以令
G
(
k
)
=
1
k
⋅
C
G(k)=1k⋅C
相关参考:
【优化算法】梯度下降法-凸函数的收敛性

评论记录:
回复评论: