引言

本节将介绍二次上界的具体作用以及它的证明过程。

回顾：

利普希兹连续

在$\text{Wolfe}$准则收敛性证明一节中简单介绍了利普希兹连续$(\text{Lipschitz Continuity})$。其定义对应数学符号表达如下：
$$\forall x,\hat{x}\in {\mathbb{R}}^n,\exists \mathcal{L}:s.t.||f(x)-f(\hat{x})||\le \mathcal{L}\cdot ||x-\hat{x}||$$
如果函数$f(\cdot )$满足利普希兹连续，对上式进行简单变换可得到：
不等式左侧可使用拉格朗日中值定理进行进一步替换。
$$\exists \xi \in (x,\hat{x})\Rightarrow \frac{||f(x)-f(\hat{x})||}{||x-\hat{x}||}=f^{\prime }(\xi )\le \mathcal{L}$$
这意味着：在函数$f(\cdot )$在定义域内的绝大部分点处的变化率存在上界，受到$\mathcal{L}$的限制。

梯度下降法介绍

在梯度下降法铺垫：总体介绍一节中对梯度下降法进行了简单认识。首先，梯度下降法是一个典型的线搜索方法$(\text{Line Search Method})$。其迭代过程对应数学符号表示如下：
$$x_{k+1}=x_k+{\alpha }_k\cdot {\mathcal{P}}_k$$

• 其中${\mathcal{P}}_k\in {\mathbb{R}}^n$，描述数值解的更新方向，在梯度下降法中，它选择目标函数$f(\cdot )$在$x_k$处梯度的反方向$-\nabla f(x_k)$作为更新方向，也称最速下降方向：
  $${\mathcal{P}}_k=-\nabla f(x_k)$$
• 而${\alpha }_k$表示步长。基于步长的选择方式分为精确搜索与非精确搜索两类。关于非精确搜索——通过迭代获取数值解序列并以此近似最优步长的方法详见：
  • $\text{Armijo}$准则
  • $\text{Glodstein}$准则
  • $\text{Wolfe}$准则

本节将介绍梯度下降法中使用精确搜索求解最优步长，以及精确搜索的限制条件——二次上界引理。

二次上界引理：介绍与作用

在求解梯度下降法的精确步长过程中，关于目标函数$f(\cdot )$，在其定义域内可微的基础上增加一个条件：目标函数的梯度函数$\nabla f(\cdot )$满足利普希兹连续。
如果是梯度函数$\nabla f(\cdot )$满足利普希兹连续，根据上面的格式，可以得到：
$${\nabla }^{2}f(\cdot )\le \mathcal{L}$$
而二阶梯度描述的是梯度$\nabla f(\cdot )$的变化量。这意味着：关于$\nabla f(\cdot )$的变化情况不会过于剧烈。相反，如果$\nabla f(\cdot )$的变化情况过于剧烈：即便迭代过程中极小的一次更新，对应函数结果的变化也极大，例如： f ( x ) = 1 x f(x)=1x

基于上述条件，可以得到结论：函数$f(\cdot )$存在二次上界。其数学符号表示为：
$$\forall x,y\in {\mathbb{R}}^n\Rightarrow f(y)\le f(x)+[\nabla f(x){]}^T\cdot (y-x)+\frac{\mathcal{L}}{2}||y-x|{|}^2$$
我们之前仅知道函数梯度$\nabla f(\cdot )$的变化率存在上界对其进行约束，但可通过该结论求出该上界的精确结果。
首先通过图像观察该结论各部分的具体意义：

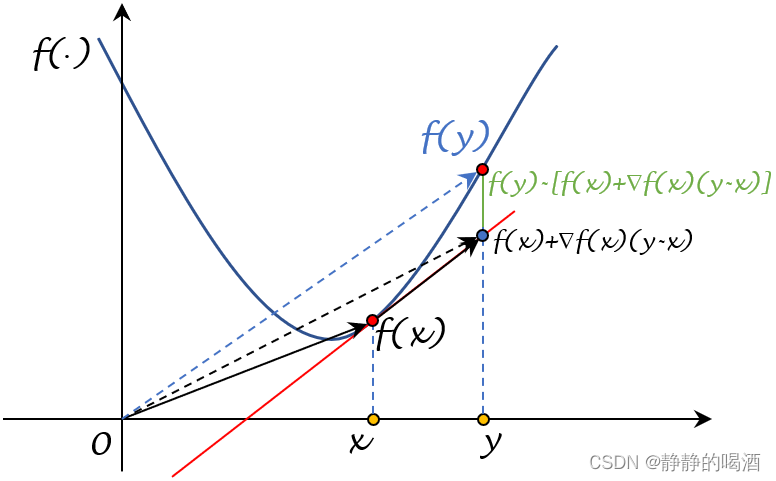
很明显，这仅是一个一维变量对应的函数结果$(\mathbb{R}\mapsto \mathbb{R})$，其中蓝色虚线箭头表示$f(y)$；黑色虚线箭头表示$f(x)+[\nabla f(x){]}^T\cdot (y-x)$。在上述结论中，两者之间的差距(绿色实线)不会无限大下去，而是存在一个上界约束这个差距：
$$f(y)-[f(x)+[\nabla f(x){]}^T\cdot (y-x)]\le \frac{\mathcal{L}}{2}||y-x|{|}^2$$
假如这个差距结果远远大于 L 2 ∣ ∣ y − x ∣ ∣ 2 L2||y−x||2

从图像中可以明显看到，如果$f(y)$与$f(x)+[\nabla f(x){]}^T(y-x)$之间的差距过大的话，那么必然是$f(y)$处的斜率与$f(x)$处的斜率差距过大产生的结果。因此这个差距上界 L 2 ∣ ∣ y − x ∣ ∣ 2 L2||y−x||2

二次上界与最优步长之间的关系

假定二次上界引理是已知的，我们观察：二次上界引理对精确步长的求解起到什么作用。
$$\forall x,y\in {\mathbb{R}}^n\Rightarrow f(y)\le f(x)+[\nabla f(x){]}^T\cdot (y-x)+\frac{\mathcal{L}}{2}||y-x|{|}^2$$
既然二次上界引理对于$\forall x,y\in {\mathbb{R}}^n$均成立，我们可以将$x,y$视作：某次迭代步骤$k$的$x_k,x_{k+1}$：
后续依然使用$x,y$进行表示。
{ x ⇒ x k y ⇒ x k + 1 y = x + α k ⋅ P k {x⇒xky⇒xk+1y=x+αk⋅Pk

• 首先对$\varphi (y)$关于$y$求解梯度：
  与$x$相关的项均视作常数。
  $$\begin{array}{rl}\nabla \varphi (y)& =0+\nabla f(x)\cdot 1+\frac{\mathcal{L}}{2}\cdot 2\cdot (y-x)\\ & =\nabla f(x)+\mathcal{L}\cdot (y-x)\end{array}$$
• 令$\nabla \varphi (y)\triangleq 0$，有：
  $$y_{min}=-\frac{\nabla f(x)}{\mathcal{L}}+x$$
  对应$\varphi (y)$的最小值$\min \varphi (y)$有：
  $$\begin{array}{rl}\min \varphi (y)& =\varphi (y_{min})\\ & =f(x)+[\nabla f(x){]}^T\cdot \left(-\frac{\nabla f(x)}{\mathcal{L}}\right)+\frac{\mathcal{L}}{2}\cdot \frac{[-\nabla f(x){]}^T[-\nabla f(x)]}{{\mathcal{L}}^2}\\ & =f(x)-\frac{||\nabla f(x)|{|}^2}{2\mathcal{L}}\end{array}$$

将$y=x+{\alpha }_k\cdot {\mathcal{P}}_k$代入，观察：

• ${\mathcal{P}}_k$是描述更新方向的向量，对应的是负梯度方向$-\nabla f(x)$；
• 同理,${\alpha }_k$对应$\begin{array}{r}\frac{1}{\mathcal{L}}\end{array}$。
  $$\{\begin{array}{l}\begin{array}{rl}y& =x+{\alpha }_k\cdot {\mathcal{P}}_k\\ y_{min}& =x+\frac{1}{\mathcal{L}}\cdot [-\nabla f(x)]\end{array}\end{array}\Rightarrow \{\begin{array}{l}\begin{array}{rl}{\alpha }_k& =\frac{1}{\mathcal{L}}\\ {\mathcal{P}}_k& =-\nabla f(x)\end{array}\end{array}$$

但需要注意的是：$f(y)\le \varphi (y)$，而$y_{min}$仅仅是$\varphi (y)$中的最小值。也就是说：$y_{min}$是$f(y)$取值上界中的最小值。在这种条件下，我们认为 α k = 1 L αk=1L

二次上界引理证明过程

条件：函数$f(\cdot )$可微，并且$\nabla f(\cdot )$满足利普希兹连续；
结论：$f(\cdot )$存在二次上界：
$$\forall x,y\in {\mathbb{R}}^n\Rightarrow f(y)\le f(x)+[\nabla f(x){]}^T\cdot (y-x)+\frac{\mathcal{L}}{2}||y-x|{|}^2$$

证明：
由于上述的$x,y\in {\mathbb{R}}^n$是定义域内任意取值，因而无法直接从条件中获取到$f(x),f(y)$之间的大小关系。这里不妨设：$y>x$，并引入辅助函数$\mathcal{G}(\theta )$：
在$x,y\in {\mathbb{R}}^n(y>x)$确定的情况下,构建一个关于$\theta$的函数，从而通过调节$\theta$来获取$[f(x),f(y)]$之间的函数结果。
G ( θ ) = f [ θ ⋅ y + ( 1 − θ ) ⋅ x ] = f [ x + θ ( y − x ) ] θ ∈ [ 0 , 1 ] G(θ)=f[θ⋅y+(1−θ)⋅x]=f[x+θ(y−x)]θ∈[0,1]

相关参考：
【优化算法】梯度下降法-二次上界