推荐|人工智能数学基础9：集合相关概念

☞ ░ 老猿Python博文目录░

一、集合基础知识

集合的特性：

确定性：给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现
互异性：一个集合中，任何两个元素都认为是不相同的，即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画，可以使用多重集，其中的元素允许出现多次
无序性：一个集合中，每个元素的地位都是相同的，元素之间是无序的。集合上可以定义序关系，定义了序关系后，元素之间就可以按照序关系排序。但就集合本身的特性而言，元素之间没有必然的序

不包含任何元素称之为空集，记为∅，空集∅是任意一个非空集合的真子集，是任何一个集合的子集
补集又可分为相对补集和绝对补集

相对补集定义：由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B或AB，即A-B={x|x∈A，且x∉B} 。
绝对补集定义：A关于全集合U的相对补集称作A的绝对补集，记作A’或∁u（A）或~A。有U’=Φ；Φ’=U

幂集：设有集合A，由集合A所有子集组成的集合，称为集合A的幂集，记作P(A) ，P(A)={x|x⊆A}。对于幂集有定理如下：有限集A的幂集的基数等于2的有限集A的基数次幂，即设集合A的元素个数|A|=n，则|P(A)|=2^n
全集：如果限定所讨论的集合都是某个集合的子集，则称该集合为全集，记作E，全集不唯一，如全集A是某个集合B的子集，则B一定也是全集
多重集：设全集为E，E中元素可以不止一次在A中出现的集合A称为多重集。若E中元素a在A中出现k次（k≥0），则称a在A中重复度为k，集合可看作重复度均小于等于1的多重集
偏序集与偏序关系：设P是集合，P上的二元关系“≤”满足以下三个条件，则称“≤”是P上的偏序关系（或部分序关系）：
（1）自反性：a≤a，∀a∈P；
（2）反对称性：∀a，b∈P，若a≤b且b≤a，则a=b；
（3）传递性：∀a，b，c∈P，若a≤b且b≤c，则a≤c；
具有偏序关系的集合P为偏序集（或称半序集），记为（P，≤）。a≤b读作“a小于或等于b”或“a含于b”，a
偏序集逆关系及对偶：设（P，≤）是偏序集，对于P中任意二元x，y有:

偏序集有如下定理：
全序集：也叫有序集，设(A，≤)是偏序集，如果(A，≤)中的关系“≤”满足条件：对于任意的a，b∈A，a≤b或b≤a至少有一个成立，那么就称关系≤为序关系，称A为在这个关系下的全序集
良序集：设集合(S,≤)为一全序集，≤是其全序关系，若对任意的S的非空子集，在其序下都有最小元素，则称≤为良序关系，(S,≤)为良序集。在数学中，集合S上的良序关系（或良序）需要满足：1.是在S上的全序关系 2.S的所有非空子集在这个次序下都存在最小元素(并非代数上的大小) 。集合S和这个良序关系一起就叫做良序集合。
模糊集：用来表达模糊性概念的集合，又称模糊集、模糊子集。普通的集合是指具有某种属性的对象的全体。这种属性所表达的概念应该是清晰的，界限分明的。因此每个对象对于集合的隶属关系也是明确的，非此即彼。但在人们的思维中还有着许多模糊的概念，例如年轻、很大、暖和、傍晚等，这些概念所描述的对象属性不能简单地用“是”或“否”来回答，而模糊集合就是指具有某个模糊概念所描述的属性的对象的全体。于概念本身不是清晰的、界限分明的，因而对象对集合的隶属关系也不是明确的、非此即彼的。这个概念我们知道即可，暂时用不着
如果两个集合S和T的元素完全相同，则称S与T两个集合相等，记为S=T ，即

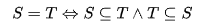
其中双箭头符号称为当且仅当，表示左边的命题与右边的命题相互蕴含，即两个命题等价。
[] 集合的表示方法通常有四种，即列举法、描述法、图像法和符号法

列举法就是将集合的元素逐一列举出来的方式,例如，光学中的三原色可以用集合{红，绿，蓝}表示、正整数集合{1,2,3，…,n,…}
描述法：形式为{代表元素|满足的性质}，如正数表示{x：x∈R且x>0}。
图像法，又称韦恩图法、韦氏图法，是一种利用二维平面上的点集表示集合的方法。一般用平面上的矩形或圆形表示一个集合，是集合的一种直观的图形表示法
符号法：有些集合可以用一些特殊符号表示，举例如下：

二、对等集合与基数

对等集合：

两个能够建立元素间一一对应的集合称为互相对等集合。例如10台电脑的集合和10部手机的集合、奇数和偶数的集合。

基数：

基数（cardinal number）：简单来说集合中元素的数目称为集合的基数。在数学上，基数是集合论中刻画任意集合大小的一个概念。根据对等这种关系对集合进行分类，凡是互相对等的集合就划入同一类。这样，每一个集合都被划入了某一类。任意一个集合A所属的类就称为集合A的基数，记作|A|（或cardA)。这样，当A 与B同属一个类时，A与B 就有相同的基数，即|A|=|B|。而当 A与B不同属一个类时，它们的基数也不同。

如果把单元素集的基数记作1，两个元素的集合的基数记作2，等等，则任一个有限集的基数就与通常意义下的自然数一致。空集的基数也记作0。于是有限集的基数也就是传统概念下的“个数”。但是，对于无穷集，传统概念没有个数，而按基数概念，无穷集也有基数，例如，任一可数集（也称可列集）与自然数集N有相同的基数，即所有可数集是等基数集。不但如此，还可以证明实数集R与可数集的基数不同。所以集合的基数是个数概念的推广。

基数的运算

基数可以比较大小。假设A，B的基数分别是a，β，即|A|=a，|B|=β，如果A与B的某个子集对等，就称 A 的基数不大于B的基数，记作a≤β，或β≥a。如果 a≤ β，但a≠β（即A与B不对等），就称A的基数小于B的基数，记作a<β，或β>a。

基数的三歧性定理——任何两个集合的基数都可以比较大小，即不存在集合A和B，使得A不能与B的任何子集对等，B也不能与A的任何子集对等。

基数可以进行运算，基数上的算术运算是对自然数运算的推广。

给定集合 X 与 Y，定义 X+Y={(x,0):x ∈ X} ∪ {(y,1):y ∈ Y}，则基数和是|X| + |Y| = |X + Y|。若 X 与 Y 不相交，则 |X| + |Y| = |X ∪ Y|。
基数积是|X||Y| = |X × Y|，其中 X × Y 是 X 和 Y 的笛卡儿积。
基数指数是|X|^|Y| = |X^Y|，其中 X^Y 是所有由 Y 到 X 的函数的集合。

在有限集时，这些运算与自然数无异。一般地：

加法和乘法是可交换的，即 |X|+|Y|=|Y|+|X| 及 |X||Y|=|Y||X|
加法和乘法符合结合律，即(|X|+|Y|)+|Z|=|X|+(|Y|+|Z|) 及 (|X||Y|)|Z|=|X|(|Y||Z|)
分配律，即 (|X|+|Y|)|Z|=|X||Z|+|Y||Z|| = |X||Y|+|X||Z|

无穷集合的加法及乘法非常简单。若 X 与 Y 皆非空而其中之一为无限集，则|X| + |Y| = |X||Y| = max{|X|, |Y|}

三、单位元

单位元也叫幺元（么元），是集合里的一种特别的元素，与该集合里的二元运算（类似于实数里的乘法*）有关。当单位元和其他元素结合时，并不会改变那些元素。

定义

设 (S,)为一带有一二元运算 的集合S（称之为原群），若S内存在一元素e:

如果对所有在S内的元素a而言，e*a=a，则e称为左单位元；
如果对所有在S内的元素a而言，a*e=a，则e称为右单位元；
若e同时为左单位元及右单位元，则称之为双边单位元，简称为单位元。

对应于加法的单位元称之为加法单位元（通常被标为0），而对应于乘法的单位元则称之为乘法单位元（通常被标为1）。

常见单位元

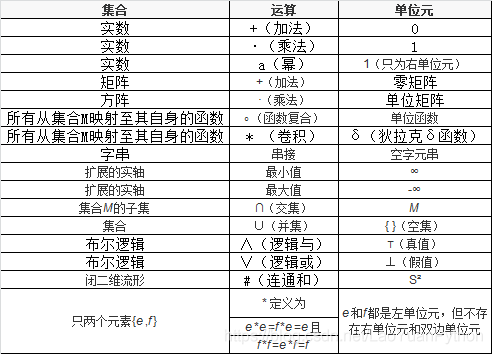
在这里插入图片描述

四、集合运算

集合的子交并补在此不介绍了，介绍一些其他的。本文下面资料参考百度文库，相关运算的描述应该是没有问题的，但相关运算符与一般看到的有比较大的差别，例如并集的运算符一般是∪而在此是[+]（也有些文档使用∨），交集的运算符一般是∩在此是[*]（也有些文档使用^），在此老猿会结合多个来源的资料将相关运算符都介绍一下。

和集：两个或两个以上集合的所有元素组成一个新集合，这个新集合称为和集。和集运算不剔除重复元素，这是和集与并集的区别。和集的运算符为[&]，如:
（1,2,3）[&]（2,3,4）=(1,2,3,2,3,4)
对称差集：两个集合中非共同的元素的集合，运算符[/]或⊕，A⊕B=(A−B)∪(B−A)，如（1,2,3）[/]（2,3,4）=（1,4）
相对补集：由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B或AB，即A-B={x|x∈A，且x∉B}
绝对补集：A关于全集合U的相对补集称作A的绝对补集，记作A'或∁u（A）、∁uA或~A

U'=Φ；Φ'=U
根据绝对补集的∁uA记法，相对补集A-B还有一种记法：∁bA或∁b（A）
绝对补集A'还有种记法：

双目运算符差集：第一个集合A减去第二个集合B所包含的元素，结果就是差集，也叫反交集，运算符为[-]，也有的记为-。差集的结果称为B对于A的补集或余集
单目运算符差集：去除集合中的重合元素，如(1,2,3,3,4)[-] = (1,2,3,4)
逆集：第二个集合减去第一个集合所包含的元素，也称为反差集，运算符[]，如（1,2,3）[]（2,3,4）=（4）
平集：两个集合的和集中，只出现一次的元素组成的集合称为平集，运算符[!]，如：（1,2,3,4）[!]（3,4,5,6）=（1,2,5,6）
频集：两个集合的和集中，出现两次以上的元素组成的集合称为频集，运算符为[!!]，如：（1,2,3,4）[!!]（3,4,5,6）=（3,4）`
求和：单目运算，求集合中所有元素的和，运算符[++]，可以放在集合前面也可以放在集合后面，如：(1,2,3)[++]=[++](1,2,3)=6
內积：单目运算，求集合或矩阵所有元素的乘积，运算符[**]，如[**](2,3,4,5)=120
算术平均值：单目运算，求集合中所有元素的算术平均值，运算符[~]，如[~](2,3,4,5)=3.5
标准方差：单目运算，集合或矩阵元素的方差的算术平方根，运算符[~~],可以在集合前或后，如：[~~][1,5,3;6,8,2;9,1,6]=2.9627,其中分号表示一行数据结束，下同
n项移动平均：单目运算，集合元素的n项移动平均，运算符[~n],如：
[~2](1,2,3,2,4,2,5)=1.5 2.5 3 3,3.5
[~3](1,2,3,2,4,2,5)=2 2.3333 2.6667 3.6667
方差：单目运算，集合或矩阵中各元素值与平均值的差的平方和的平均数，运算符号[~^]，如：
·（1,5,3,6,8,2,9,1,6）[~^]=8.7778`
频数表：单目运算，集合中每个元素出现的个数，运算符号[^]，有四种形式：

[^]或[^1]，按出现次数降序排列
[^2]按出现次数升序排列
[^3]按元素大小降序排列
[^4]按元素大小升序排列

矩阵求逆：单目运算，对集合中的元素按矩阵方式求逆，N阶矩阵A、B，如AB=1则称B是A的逆矩阵。矩阵求逆的运算符为[-1],如：
（1,5,3;6,8,2;9,1,6）[-1]=-0.1901 0.1116 0.0579 0.0744 0.0868 0.0661
中值：也叫中间值，单目运算，对集合中的元素升序排列，处在中间的值称为中值，运算符号[|]，如：(1,2,3,2,4,2,5)[|] = 3
众数：也称典型值，单目运算，在集合中出现次数最多的元素及其次数，运算符号[||]，如：(1,2,2,3,4,4)[||]=2 2、4 2，表示2和4出现次数最多，都出现了2次
累加数列：单目运算，对集合中排列的元素逐个累加得到的数列，首个元素无需相加取自身的值作为结果，后面每个元素都与前面累加的结果相加得到当前项，运算符号[&+]，如：
[&+](1,2,3,4,5)=1 3 6 10 15
累减数列：单目运算，数列中的元素后一个减前一个元素得到的数列，首个元素无需相减取自身的值作为结果，累加数列的逆运算，运算符号[&-]，如：
[&-](1,3,6 ,10,15)=1,2,3,4,5
倒数数列：单目运算，集合中的每个元素求倒数组成的新集合，运算符号[&/]，如：
[&/](1,2,4 ,10)=1,0.5,0.25,0.1
倒数和：单目运算，集合中的每个元素求倒数的和，运算符号[/+]，如：
[&/](1,2,4 ,10)=1.85
几**何平均值：也叫级均值，单目运算，集合內积的开n次方,n为元素个数，运算符号[*~]，如：（1,2,4）[*~]=2
调和平均值：也叫谐均值，单目运算，集合所有元素倒数的平均数的倒数，运算符号[/~]，如：
[/~](1,2,4 ,10)=2.162
最小值：单目运算，集合所有元素的最小值，运算符号[<]
最大值：单目运算，集合所有元素的最大值，运算符号[>]
降序排序：单目运算，集合所有元素进行降序排列，运算符号[>>]
升序排序：单目运算，集合所有元素进行升序排列，运算符号[<<]
反转：单目运算，集合所有元素倒序排列，运算符号[<>]
极差：单目运算，集合或矩阵最大数减最小数的值，运算符号[><]
转置：单目运算，对数列或矩阵进行转置，运算符号[T]，将矩阵的行变成列，列变成行
数据个数：单目运算，返回集合中元素个数，运算符号[N]
第n个元素值：单目运算，取出集合中第n个元素值，运算符号[n],其中n为具体序号（从1开始），如(1,2,3)[2]=2
第i行第j列值：单目运算，获得矩阵第i行第j列值，i、j从1开始计数，如：(1,2,3;4,5,6)[2,1]=4
行数：单目运算，获得矩阵的总行数，运算符[R]，如：(1,2,3;4,5,6)[R]=2
取出行：单目运算，获得矩阵的指定行数据，运算符[Rn],n为具体行号，从1开始计数，如：(1,2,3;4,5,6)[R1]=1 2 3
取出部分行：单目运算，获得矩阵的指定行数据，运算符[Ri,j],i、j为具体行号，从1开始计数，如：(1,2,3;4,5,6;7,8,9)[R1,2]=1 2 3;4,5,6
添加行：双目运算，将第二个矩阵加到第一个矩阵后面，运算符[+R]
添加1行：双目运算，将第二个矩阵的指定行加到第一个矩阵后面，运算符[+Ri]，i为具体行号，从1开始计数
单目运算行交换：将矩阵的第i行与第j行数据进行交换，运算符[Ri=Rj],i、j为具体行号，从1开始计数，如：(1,2,3;4,5,6)[R1=R2]=4,5,6;1 2 3
双目运算行替换：将矩阵1的第i行替换为矩阵2第j行数据，运算符[Ri=Rj],i、j为具体行号，从1开始计数，如：(1,2,3;4,5,6)[R1=R2]（7,8,9；0,2,4）=0,2,4；4,5,6
列数：单目运算，获得矩阵的列数，运算符[C]
取出矩阵的指定列：单目运算，获得矩阵指定列，运算符[Ci]，i为列号，从1开始计数
取出部分列：单目运算，获得矩阵部分列，运算符[Ci,j]，i、j为列号，从1开始计数
增加1列：双目运算，把第二个矩阵的指定列添加到第一个矩阵后面，运算符[+Ci],i为第二个矩阵列号，从1开始计数，如：(1,2,3;4,5,6)[+c1](7,8,9;0,2,4)=(1,2,3,7;4,5,6,0)
单目运列交换：将矩阵的第i列与第j列数据进行交换，运算符[Ci=Cj],i、j为具体列号，从1开始计数
双目运算行替换：将矩阵1的第i列替换为矩阵2第j列数据，运算符[Ci=Cj],i、j为具体列号，从1开始计数

五、集合运算定律

交换律：A∩B=B∩A；A∪B=B∪A
结合律：A∪(B∪C)=(A∪B)∪C；A∩(B∩C)=(A∩B)∩C
分配对偶律：A∩(B∪C)=(A∩B)∪(A∩C)；A∪(B∩C)=(A∪B)∩(A∪C)
同一律：A∪∅=A；A∩U=A
求补律：A∪A’=U；A∩A’=∅
对合律：A’’=A
等幂律：A∪A=A；A∩A=A
零一律：A∪U=U；A∩∅=∅
吸收律：A∪(A∩B)=A；A∩(A∪B)=A
反演律（德·摩根律）：(A∪B)’=A’∩B’；(A∩B)’=A’∪B’。文字表述：1.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集; 2.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集。
注：有个集合的对偶律，老猿理解跟反演律是一回事，因此在此没有单列
容斥原理：
card(A∪B)=card(A)+card(B)-card(A∩B)
card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)
应用案例：
问题：假设有100人参加了三个兴趣小组。其中参加数学兴趣小组的有55人，参加语文兴趣小组的有65人，参加英语兴趣小组的有70人，同时参加语文和数学兴趣小组的人数是31人，同时参加数学和英语兴趣小组的人数是40人，同时参加语文和英语兴趣小组的有25人，则三个兴趣小组都参加的人数是多少人?
解答：(1) A+B+T=至少参与一项的总人数(无重叠)
　　(2) A+2B+3T=至少参与一项的总人数(含重叠部分)
　　(3) B+3T=至少参与两项的总人数(含重叠)
　　(4) T三项都参与的人数。
　　这里介绍一下A、B、T分别是什么：
　　A=x+y+z;表示只参加一个兴趣小组的人数
　　B=a+b+c;表示仅参加了两个兴趣兴趣小组的人数
　　T=全部都参加的人数。
　　通过公式有如下解法：
　　(1) A+B+T=100;
　　(2) A+2B+3T=55+65+70=190
　　(3) B+3T=31+40+25=96
　　实际上我们要求的是T， (1)+(3)-(2)=T。即得到答案T=100+96-190=6

六、小结

本文介绍了集合一些相关的基础概念、运算及定律，包括基数、对等集合、单位元以及类似补集、差集、对称差集等概念，这些知识对于阅读AI、线性代数等相关知识有一定的帮助。

参考文档：

百度百科

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

更多人工智能数学基础的介绍请参考专栏《人工智能数学基础》
专栏网址：http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10382948.html

关于老猿的付费专栏

付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 http://iyenn.com/rec/324324.html 使用PyQt开发图形界面Python应用专栏目录》；
付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《http://iyenn.com/rec/324326.html moviepy音视频开发专栏文章目录》；
付费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《http://iyenn.com/rec/324329.html OpenCV-Python初学者疑难问题集专栏目录》。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《http://iyenn.com/index/link?url=https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░

文章知识点与官方知识档案匹配，可进一步学习相关知识

Python入门技能树人工智能机器学习工具包Scikit-learn333560 人正在系统学习中

老猿Python

微信公众号

专注Python相关语言、图像音视频处理、AI