二叉搜索树完全解析：从理论到C++手把手实现

一、二叉搜索树的概念

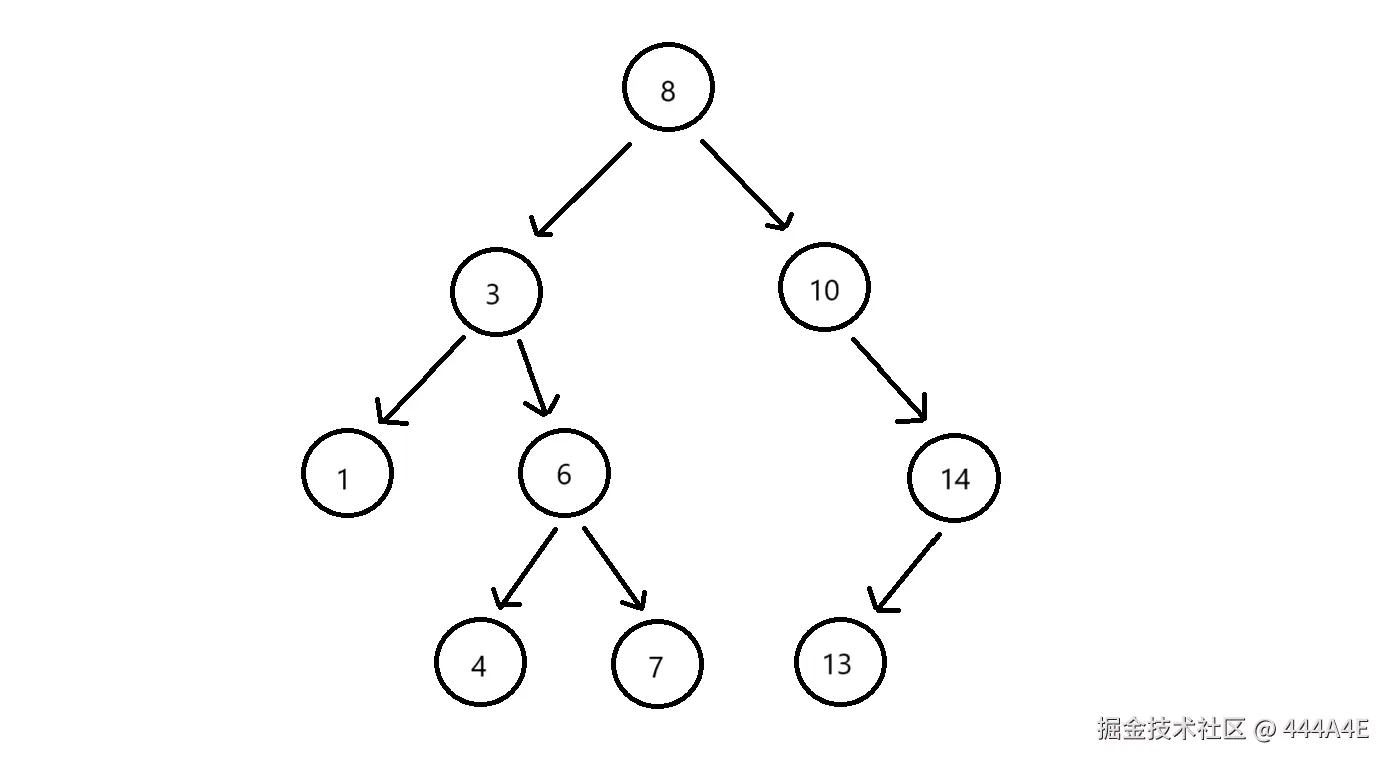
二叉搜索树又称二叉排序树，它可以是一颗空树，或者是具有以下性质的二叉树：

  • 若左子树不为空，则左子树上所有节点的值都小于等于根节点的值。
  • 若右子树不为空，则右子树上所有节点的值都大于等于根节点的值。
  • 左右子树也分别是二叉搜索树。
  • 分场景可以支持插入相等值或不支持插入相等值，map/set/multimap/multiset系列容器底层就是二叉搜索树，其中map/set不支持插入相等值，multimap/multiset支持插入相等值。这些后面文章再说。

image.png

二、二叉搜索树的性能分析

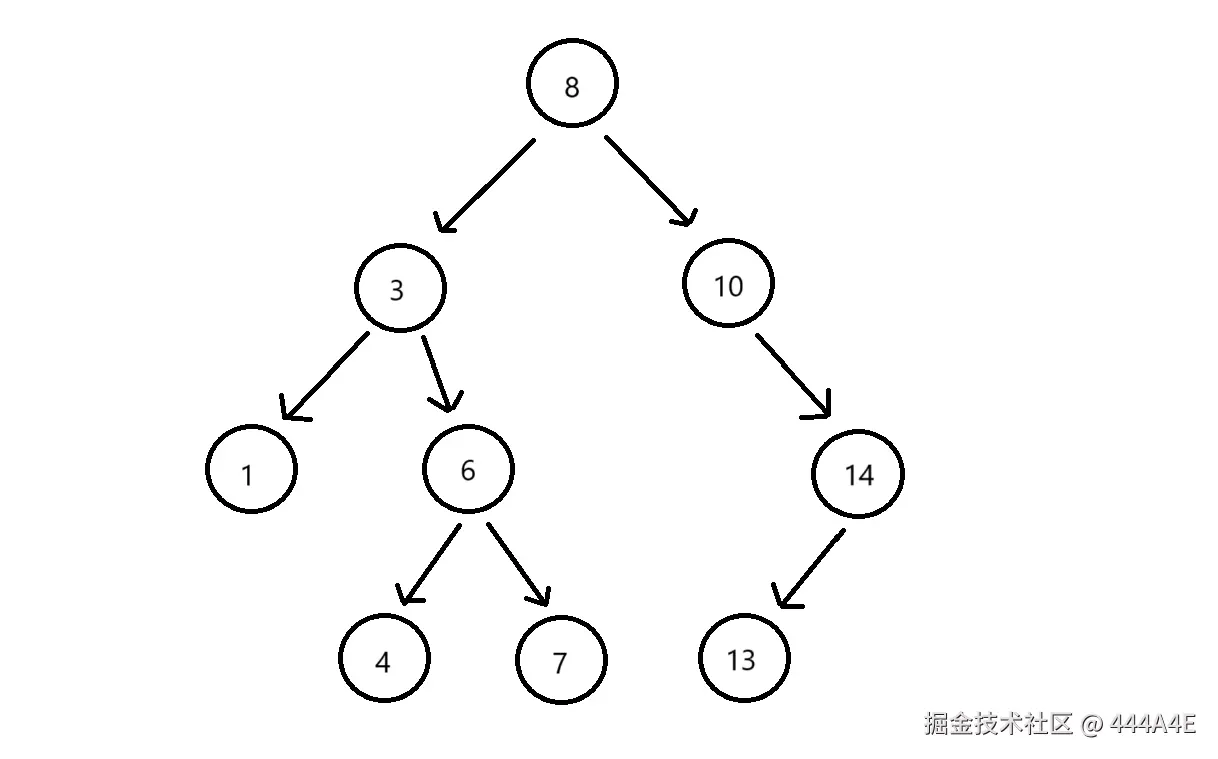
最优情况下二叉搜索树为完全二叉树或者接近完全二叉树，其高度为log2Nlog2N。最差情况下，二叉搜索树退化为单枝树，其高度为NN。所以综合而言二叉搜索树增删改查时间复杂度为O(N)O(N)。

但是这样的效率无法满足需求，所以还有二叉树的变形结构：平衡二叉树、AVL树、红黑树，这些也放在后面的文章中。

image.png

image.png

三、二叉搜索树的插入

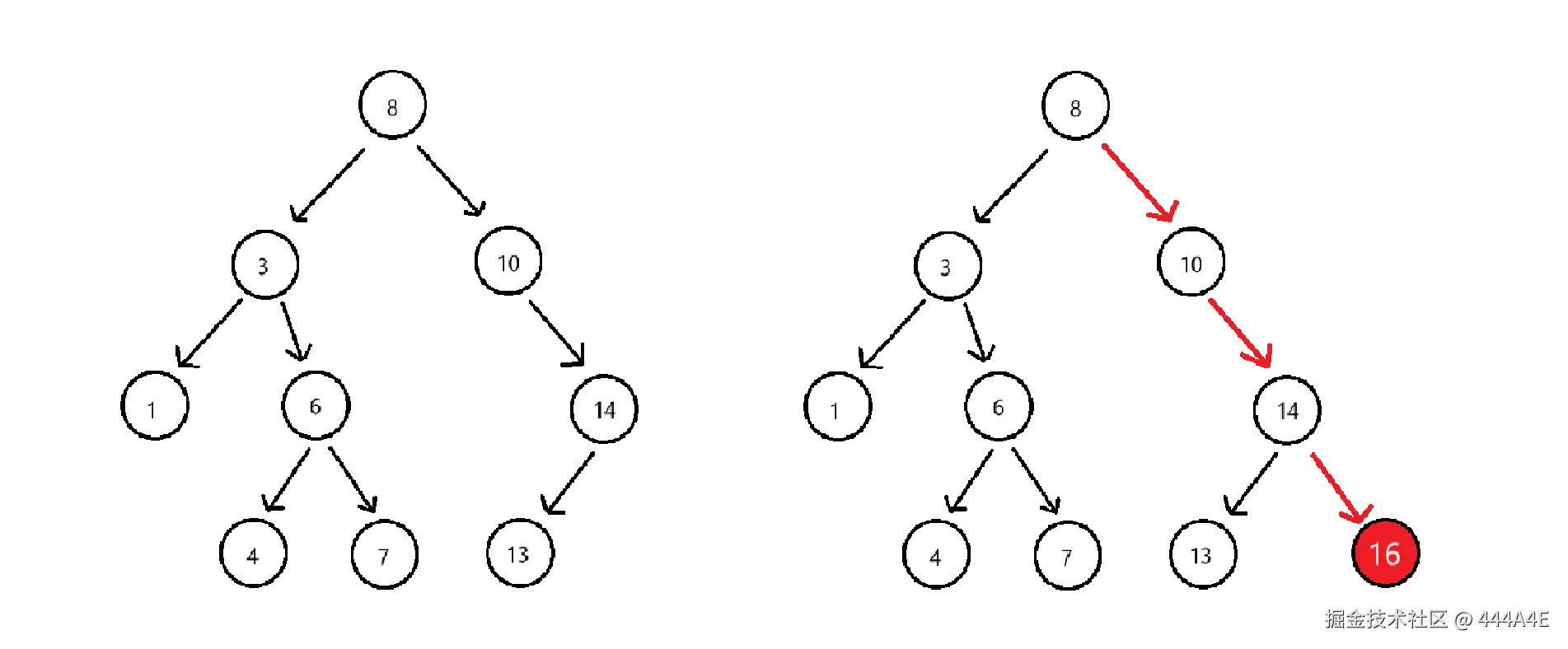
  1. 树为空直接新增节点给root
  2. 树不为空，插入节点值比当前节点大往右走，插入值比当前节点小往左走，到空位置插入。
  3. 如果支持插入相等值，可以向左也可以向右，但后续插入需保持一致性。

image.png

image.png

四、二叉搜索树的查找

假设查找的值为x：

  1. 从根开始比较，x比根的值大向右找，x比根值小则向左找。
  2. 走到为空则x不存在。
  3. 如果不支持插入相同值则找到x即可返回。
  4. 如支持插入相同值，一般为查找中序遍历的第一个x。

五、二叉搜索树的删除

首先查找元素是否在树中，不存在返回false，存在则分四种情况处理（假设要删除的节点为N）：

  1. N的左右子节点均为空。
  2. N的左子节点为空，右不为空。
  3. N的右子节点为空，左不为空。
  4. N的左右子节点均不为空。

解决办法：

  1. 直接删除N节点，将N的父节点指向N节点的指针置空（这种情况可以直接和2、3情况一起处理，效果相同）。
  2. 改变N节点的父节点指针，指向N的右子节点，删除N节点。
  3. 改变N节点的父节点指针，指向N的左子节点，删除N节点。
  4. 替换法删除：找N节点左子树中的最大节点，也就是左子树中的最右节点（假设为R），或者是N节点右子树中的最小节点，也就是右子树中的最左节点（假设为R），来替换N节点（也就是交换N节点和R节点的值），然后删除R节点。

情况1和情况2：删除1和10

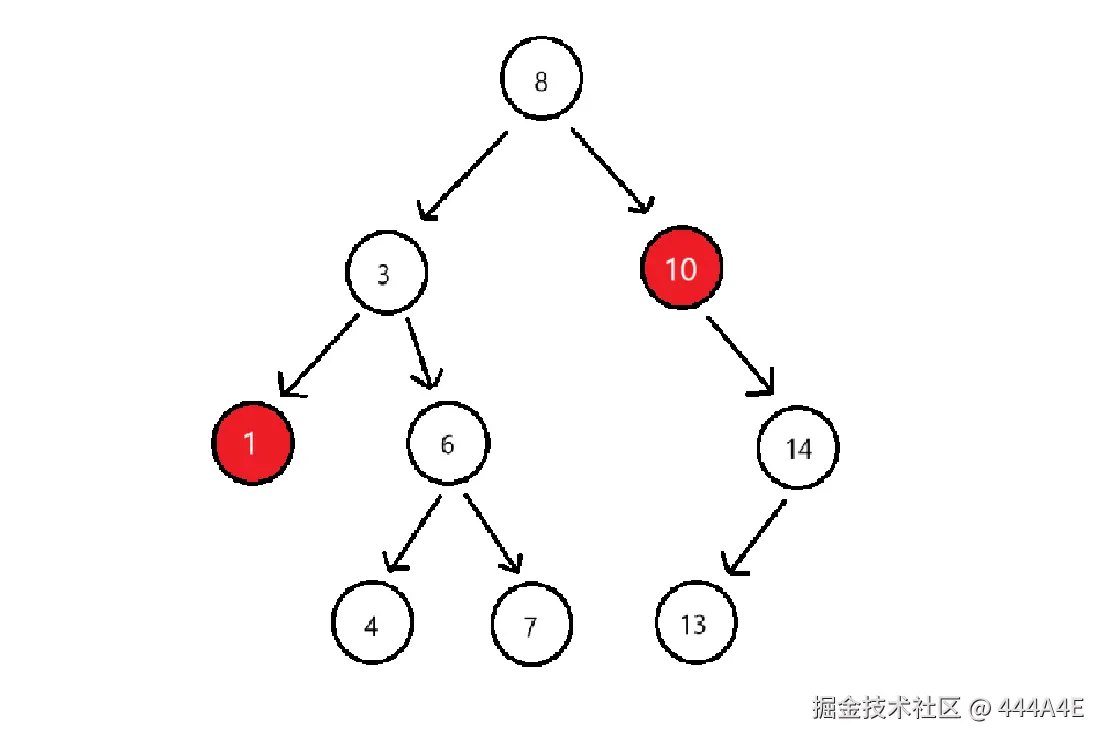image.png 情况3：删除14

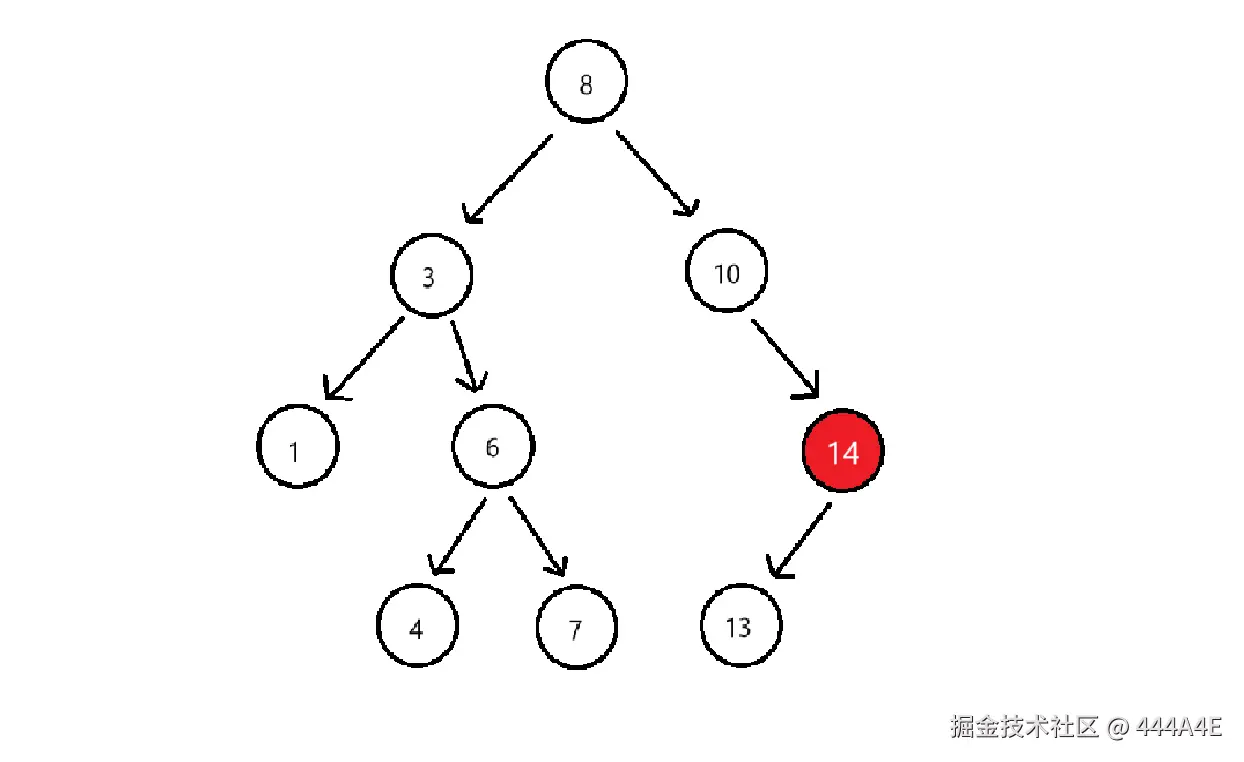
image.png

情况4：删除3和8

image.png

六、二叉搜索树的代码实现

cpp
 代码解读
复制代码
namespace Key
{
	template<class K>
	struct TreeNode
	{
		K _key;
		TreeNode* _left;
		TreeNode* _right;
		TreeNode(const K& key) :_key(key), _left(nullptr), _right(nullptr) {}
	};

	template<class K>
	class BinarySearchTree
	{
		typedef TreeNode Node;
	public:
		// 插入
		bool insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}

			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(key);
			if (cur->_key > parent->_key) { parent->_right = cur; }
			else { parent->_left = cur; }
			return true;
		}

		// 查找   
		bool find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (key > cur->_key) { cur = cur->_right; }
				else if (key < cur->_key) { cur = cur->_left; }
				else { return true; }
			}
			return false;
		}

		// 删除
		bool erase(const K& key)
		{
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root) { _root = cur->_right; }
						else
						{
							// 左为空
							if (cur == parent->_left) { parent->_left = cur->_right; }
							else { parent->_right = cur->_right; }
							delete cur;
						}
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root) { _root = cur->_left; }
						else
						{
							// 右为空
							if (cur == parent->_left) { parent->_left = cur->_left; }
							else { parent->_right = cur->_left; }
							delete cur;
						}
					}
					else
					{
						// 找右子树的最小节点
						Node* replaceParent = cur;
						Node* replace = cur->_right;
						while (replace->_left)
						{
							replaceParent = replace;
							replace = replace->_left;
						}

						swap(replace->_key, cur->_key);
						if (replaceParent->_left == replace) { replaceParent->_left = replace->_right; }
						else { replaceParent->_right = replace->_right; }
						delete replace;
					}
					return true;
				}
			}
			return false;
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}
		// 中序遍历
		void _InOrder(Node* root)
		{
			if (root == nullptr){ return; }
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}

	private:
		Node* _root = nullptr;
	};
}

七、二叉搜索树 key 和 key/value 使用场景

7.1 key 搜索场景

只有key作为关键码，结构中只需存储key即可，关键码即为要搜索到的值，搜索时只需要判断key在不在。这样的二叉搜索树支持增删查，但不支持修改，因为修改key会破坏搜索树的结构。

场景一：无人值守车库，小区买了车位的车主才能进小区，那么物业只需要把买了车位的车主车牌号录入系统，车辆进入时扫描车牌是否在系统中，在则放行，否则无法进入。

场景二：检查单词拼写是否正确，将词库所有单词放入搜索二叉树，读取单词是否在搜索树中，不在则波浪线标红提示。

7.2 key/value 搜索场景

每一个关键码key都有与之对应的value，value可以是任意类型对象。树的节点除了存储key还需要存储value，增删查以key为关键字进行比较，找到对应的value。key/value的场景不支持修改key，因为会破坏结构，支持修改value。

场景一：商场无人值守车库，车辆进入时扫描车牌并记录入场时间，车辆离开时扫描车牌查找时间，用当前时间减入场时间，计算出停车费用。

场景二：英汉互译字典，节点存储key（英文） 和 value（中文），搜索输入英文查找对应的中文。

7.3 key/value 二叉搜索树代码实现

cpp
 代码解读
复制代码
namespace Key_value
{
	template<class K, class V>
	struct TreeNode
	{
		K _key;
		V _value;
		TreeNode* _left;
		TreeNode* _right;
		TreeNode(const K& key, const V& value) :_key(key), _value(value), _left(nullptr), _right(nullptr) {}
	};

	template<class K, class V>
	class BinarySearchTree
	{
		typedef TreeNode Node;
	public:
		BinarySearchTree() = default;
		BinarySearchTree(const BinarySearchTree& BSTree) { _root = _copy(BSTree._root); }

		BinarySearchTree& operator=(BinarySearchTree BSTree)
		{
			swap(_root, BSTree._root);
			return *this;
		}

		~BinarySearchTree()
		{
			_Destory(_root);
			_root = nullptr;
		}
		
		// 插入
		bool insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key, value);
				return true;
			}

			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(key, value);
			if (cur->_key > parent->_key) { parent->_right = cur; }
			else { parent->_left = cur; }
			return true;
		}
		// 查找   
		Node* find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (key > cur->_key) { cur = cur->_right; }
				else if (key < cur->_key) { cur = cur->_left; }
				else { return cur; }
			}
			return nullptr;
		}

		bool erase(const K& key)
		{
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root) { _root = cur->_right; }
						else
						{
							// 左为空
							if (cur == parent->_left) parent->_left = cur->_right;
							else parent->_right = cur->_right;
							delete cur;
						}
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root) { _root = cur->_left; }
						else
						{
							// 右为空
							if (cur == parent->_left) { parent->_left = cur->_left; }
							else { parent->_right = cur->_left; }
							delete cur;
						}
					}
					else
					{
						// 找右子树的最小节点
						Node* replaceParent = cur;
						Node* replace = cur->_right;
						while (replace->_left)
						{
							replaceParent = replace;
							replace = replace->_left;
						}

						swap(replace->_key, cur->_key);
						swap(replace->_value, cur->_value);
						if (replaceParent->_left == replace) { replaceParent->_left = replace->_right; }
						else { replaceParent->_right = replace->_right; }
						delete replace;
					}
					return true;
				}
			}
			return false;
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}

	private:
		Node* _root = nullptr;

		// 中序遍历
		void _InOrder(Node* root)
		{
			if (root == nullptr) { return; }
			_InOrder(root->_left);
			cout << root->_key << ":" << root->_value << " ";
			_InOrder(root->_right);
		}
		// 清理
		void _Destory(Node* root)
		{
			if (root == nullptr) { return; }
			_Destory(root->_left);
			_Destory(root->_right);
			delete root;
		}

		Node* _copy(Node* root)
		{
			if (root == nullptr) { return nullptr; }
			Node* newRoot = new Node(root->_key, root->_value);
			newRoot->_left = _copy(root->_left);
			newRoot->_right = _copy(root->_right);
			return newRoot;
		}
	};
}
注：本文转载自juejin.cn的444A4E的文章"https://juejin.cn/post/7493007413734998035"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！