

在上一篇中,我们通过题目“最长上升子序列”以及"最大子序和",学习了DP(动态规划)在线性关系中的分析方法。这种分析方法,也在运筹学中被称为“线性动态规划”,具体指的是 “目标函数为特定变量的线性函数,约束是这些变量的线性不等式或等式,目的是求目标函数的最大值或最小值”。这点大家作为了解即可,不需要死记,更不要生搬硬套!
在本节中,我们将继续分析一道略微区别于之前的题型,希望可以由此题与之前的题目进行对比论证,进而顺利求解!
01
第120题:三角形最小路径和
第120题:给定一个三角形,找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
本题有一定难度!
如果没有思路请回顾上一篇的学习内容!
不建议直接看题解!
02
自顶向下图解分析

首先我们分析题目,要找的是三角形最小路径和,这是个啥意思呢?假设我们有一个三角形:[[2], [3,4], [6,5,7], [4,1,8,3]]
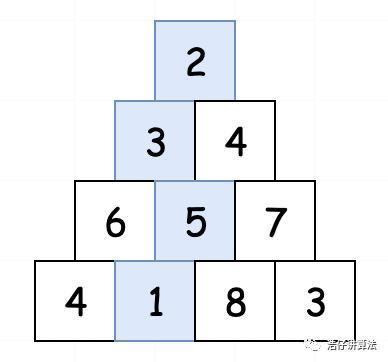
那从上到下的最小路径和就是2-3-5-1,等于11。
由于我们是使用数组来定义一个三角形,所以便于我们分析,我们将三角形稍微进行改动:
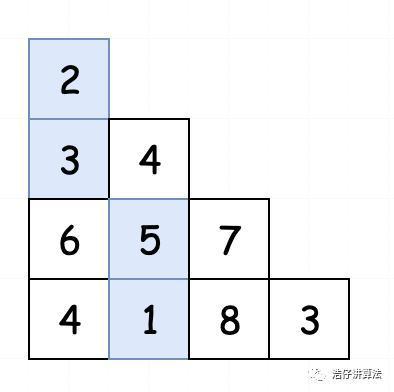
这样相当于我们将整个三角形进行了拉伸。这时候,我们根据题目中给出的条件:每一步只能移动到下一行中相邻的结点上。其实也就等同于,每一步我们只能往下移动一格或者右下移动一格。将其转化成代码,假如2所在的元素位置为[0,0],那我们往下移动就只能移动到[1,0]或者[1,1]的位置上。假如5所在的位置为[2,1],同样也只能移动到[3,1]和[3,2]的位置上。如下图所示:
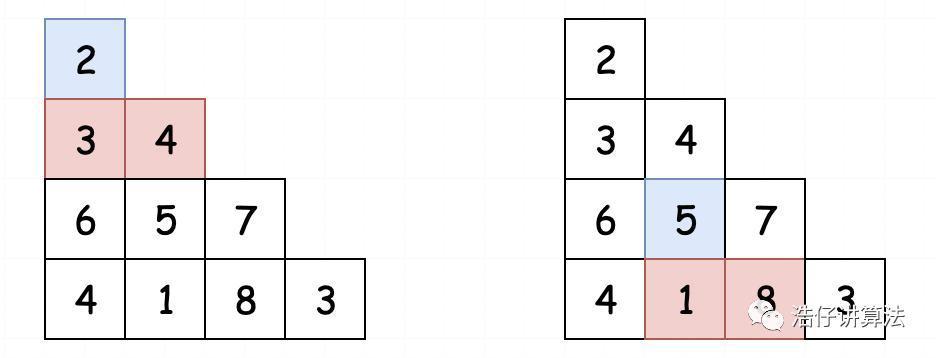
题目明确了之后,现在我们开始进行分析。题目很明显是一个找最优解的问题,并且可以从子问题的最优解进行构建。所以我们通过动态规划进行求解。首先,我们定义状态:
dp[i][j] : 表示包含第i行j列元素的最小路径和
我们很容易想到可以自顶向下进行分析。并且,无论最后的路径是哪一条,它一定要经过最顶上的元素,即[0,0]。所以我们需要对dp[0][0]进行初始化。
dp[0][0] = [0][0]位置所在的元素值
继续分析,如果我们要求dp[i][j],那么其一定会从自己头顶上的两个元素移动而来。
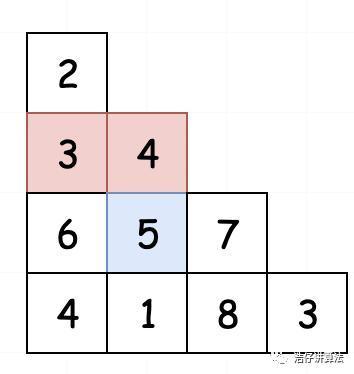
如5这个位置的最小路径和,要么是从2-3-5而来,要么是从2-4-5而来。然后取两条路径和中较小的一个即可。进而我们得到状态转移方程:
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j]) + triangle[i][j]
但是,我们这里会遇到一个问题!除了最顶上的元素之外,
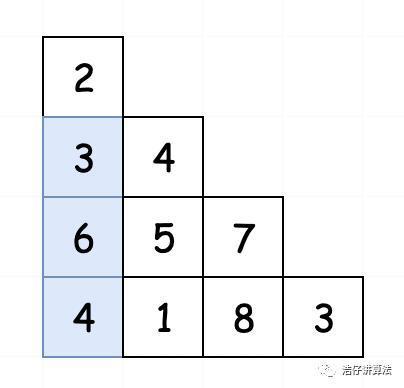
最左边的元素只能从自己头顶而来。(2-3-6-4)
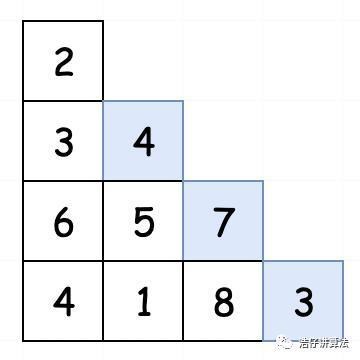
最右边的元素只能从自己左上角而来。(2-4-7-3)
然后,我们观察发现,位于第2行的元素,都是特殊元素(因为都只能从[0,0]的元素走过来)
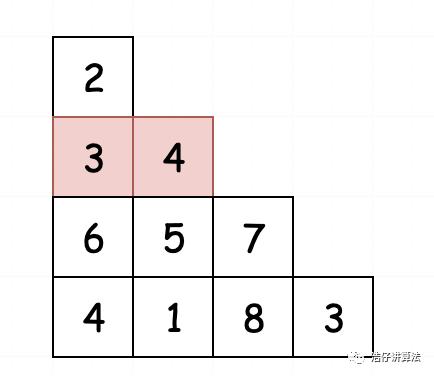
我们可以直接将其特殊处理,得到:
dp[1][0] = triangle[1][0] + triangle[0][0]
dp[1][1] = triangle[1][1] + triangle[0][0]
最后,我们只要找到最后一行元素中,路径和最小的一个,就是我们的答案。即:
l:dp数组长度
result = min(dp[l-1,0],dp[l-1,1],dp[l-1,2]....)
综上我们就分析完了,我们总共进行了4步:
定义状态
总结状态转移方程
分析状态转移方程不能满足的特殊情况。
得到最终解
03
代码分析
分析完毕,代码自成:
- 1func minimumTotal(triangle [][]int) int {
- 2 if len(triangle) < 1 {
- 3 return 0
- 4 }
- 5 if len(triangle) == 1 {
- 6 return triangle[0][0]
- 7 }
- 8 dp := make([][]int, len(triangle))
- 9 for i, arr := range triangle {
- 10 dp[i] = make([]int, len(arr))
- 11 }
- 12 result := 1<<31 - 1
- 13 dp[0][0] = triangle[0][0]
- 14 dp[1][1] = triangle[1][1] + triangle[0][0]
- 15 dp[1][0] = triangle[1][0] + triangle[0][0]
- 16 for i := 2; i < len(triangle); i++ {
- 17 for j := 0; j < len(triangle[i]); j++ {
- 18 if j == 0 {
- 19 dp[i][j] = dp[i-1][j] + triangle[i][j]
- 20 } else if j == (len(triangle[i]) - 1) {
- 21 dp[i][j] = dp[i-1][j-1] + triangle[i][j]
- 22 } else {
- 23 dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
- 24 }
- 25 }
- 26 }
- 27 for _,k := range dp[len(dp)-1] {
- 28 result = min(result, k)
- 29 }
- 30 return result
- 31}
- 32
- 33func min(a, b int) int {
- 34 if a > b {
- 35 return b
- 36 }
- 37 return a
- 38}

运行上面的代码,我们发现使用的内存过大。我们有没有什么办法可以压缩内存呢?通过观察我们发现,在我们自顶向下的过程中,其实我们只需要使用到上一层中已经累积计算完毕的数据,并且不会再次访问之前的元素数据。绘制成图如下:
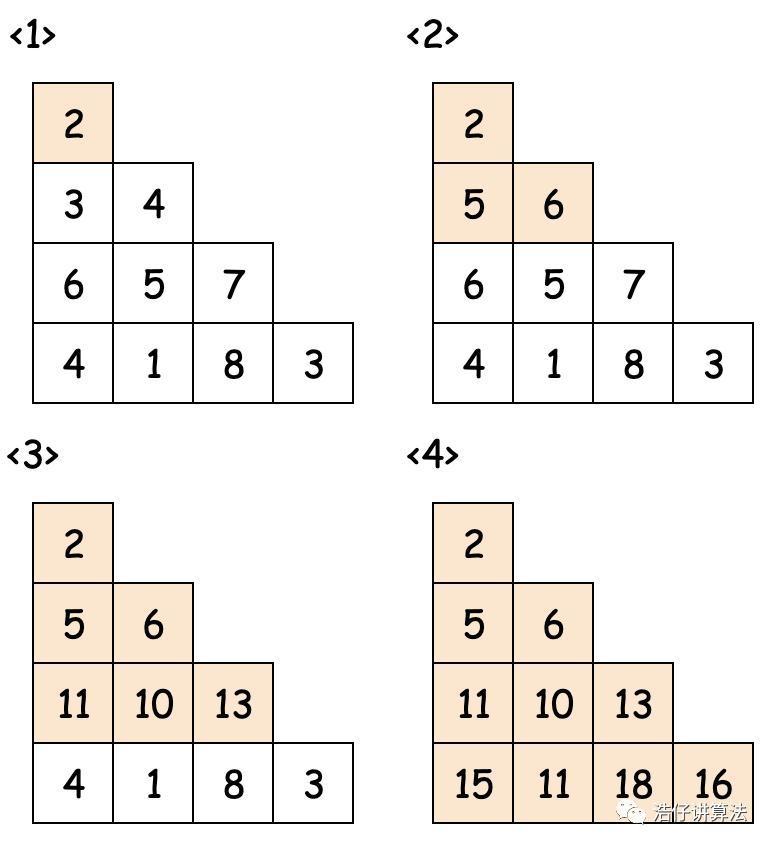
优化后的代码如下:
- 1func minimumTotal(triangle [][]int) int {
- 2 l := len(triangle)
- 3 if l < 1 {
- 4 return 0
- 5 }
- 6 if l == 1 {
- 7 return triangle[0][0]
- 8 }
- 9 result := 1<<31 - 1
- 10 triangle[0][0] = triangle[0][0]
- 11 triangle[1][1] = triangle[1][1] + triangle[0][0]
- 12 triangle[1][0] = triangle[1][0] + triangle[0][0]
- 13 for i := 2; i < l; i++ {
- 14 for j := 0; j < len(triangle[i]); j++ {
- 15 if j == 0 {
- 16 triangle[i][j] = triangle[i-1][j] + triangle[i][j]
- 17 } else if j == (len(triangle[i]) - 1) {
- 18 triangle[i][j] = triangle[i-1][j-1] + triangle[i][j]
- 19 } else {
- 20 triangle[i][j] = min(triangle[i-1][j-1], triangle[i-1][j]) + triangle[i][j]
- 21 }
- 22 }
- 23 }
- 24 for _,k := range triangle[l-1] {
- 25 result = min(result, k)
- 26 }
- 27 return result
- 28}
- 29
- 30func min(a, b int) int {
- 31 if a > b {
- 32 return b
- 33 }
- 34 return a
- 35}

课后思考:如何自下而上求解?评论区留言吧!
注:本系列所有教程中都不会用到复杂的语言特性,大家不需要担心没有学过go。算法思想最重要,使用go纯属本人爱好。同时,本系列所有代码均在leetcode上进行过测试运行,保证其严谨性!
温馨提示
浩仔讲算法~
每天一起学习图解漫画算法。
一起刷题,一起成长!
~长按下方二维码进行关注吧~

关注后有资源~


评论记录:
回复评论: