目录
0 前言
本文为李宏毅学习笔记——2024春《GENERATIVE AI》篇——作业笔记HW4的补充内容1。
如果你还没获取到LLM API,请查看我的另一篇笔记:
HW1~2:LLM API获取步骤及LLM API使用演示:环境配置与多轮对话演示-CSDN博客
完整内容参见:
李宏毅学习笔记——2024春《GENERATIVE AI》篇
在正式进入实践之前,你需要知道 LoRA 的基础概念,这篇文章会带你从线性层的 LoRA 实现到注意力机制。
我之前的“手把手带你实战Transformers”学习笔记中也简单介绍过各类参数高效微调的方法以及Lora 原理与实战。
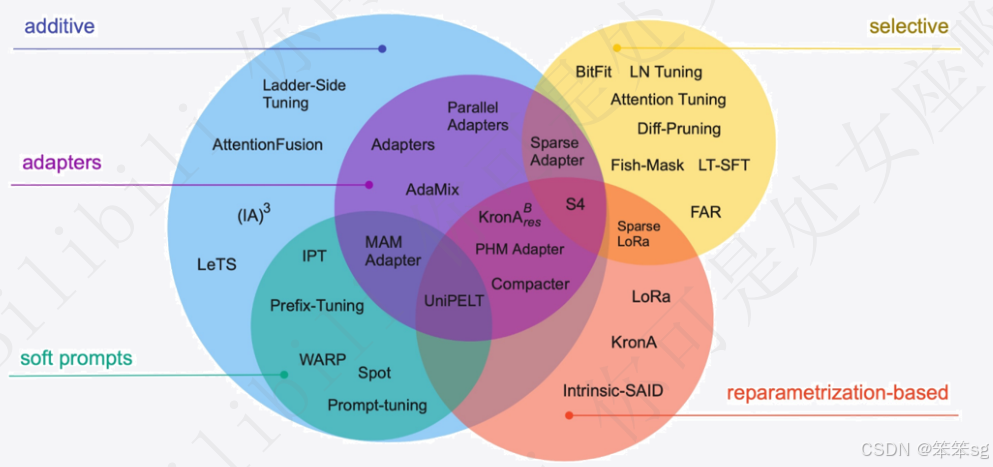
感兴趣的可以简单浏览一下,链接如下:
3.1 参数高效微调与BitFit实战_bitfit微调-CSDN博客
如果你曾使用过 AI 生图,那么一定对 LoRA 有印象,下图来自 Civitai LoRA,上面有很多可供下载的 LoRA 模型。
你可能也曾疑惑于为什么只导入 LoRA 模型不能生图?读下去,你会解决它。
1 为什么需要LoRA?
这篇文章将从基础的线性层开始,带你一步步了解 LoRA 的核心思想,并深入探索它在注意力机制中的应用。
LoRA,全称 Low-Rank Adaptation,是一种用于微调大型预训练模型的技术。它的核心思想是通过 低秩分解(常见的形式是奇异值分解)减少微调时的参数量,而不牺牲模型的性能。
论文原文:LoRA: Low-Rank Adaptation of Large Language Models

大型预训练模型的出现,为我们带来了强大的自然语言处理和计算机视觉能力,这是一个推动时代的成功。但大模型的“大”,不仅体现在其参数量上,更体现在我们无法轻松进行微调 :),全量微调一个预训练大模型的代价非常高,而且一般的设备根本训练不动。而 LoRA 提供了一种高效的微调方法,使得在小型设备上微调大模型成为可能。
根据论文中的描述:
- Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times.
相比于对 GPT-3 175B 模型使用全量参数的微调,LoRA 减少了训练参数量的 10,000 倍,GPU 显存需求的 3 倍。
- LoRA performs on-par or better than fine-tuning in model quality on RoBERTa, DeBERTa, GPT-2, and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency.
LoRA 的可训练参数更少,但在 RoBERTa、DeBERTa、GPT-2 和 GPT-3 上的模型质量与全量微调相当甚至更好,而且不会增加推理延迟。
2 LoRA的核心思想
LoRA 的核心在于利用低秩分解来近似模型权重的更新。
2.1 低秩分解
在线性代数中,任何矩阵都可以分解为多个低秩矩阵的乘积。例如,一个大的矩阵 W 可以近似表示为两个小矩阵 B 和 A 的乘积:
ΔW=BA
其中:
- A∈
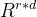 , r 是低秩值, d 是输入特征维度。
, r 是低秩值, d 是输入特征维度。 - B∈
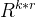 , k 是输出特征维度。
, k 是输出特征维度。
通过训练这两个小矩阵,我们可以近似地更新原始权重矩阵 W,而无需训练整个大的 W。
2.2 应用到神经网络中的线性层
在线性层中,前向传播的计算为:
y=Wx+b
其中:
- x∈
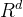 是输入向量。
是输入向量。 - W∈
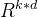 是权重矩阵。
是权重矩阵。 - b∈
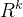 是偏置向量。
是偏置向量。 - y∈
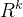 是输出向量。
是输出向量。
在微调过程中,通常需要更新 W 和 b。但在 LoRA 中,我们可以冻结原始的 W,仅仅在其基础上添加一个可训练的增量 ΔW:
y=(W+ΔW)x+b
其中:
ΔW=BA
通过训练 A 和 B,我们大大减少了需要更新的参数数量。
2.2.1 参数量对比
假设:
- 输入特征维度为 d
- 输出特征维度为 k
- 低秩值为 r(通常 r≪min(d,k))
1)全量微调:
- 需要训练的参数数量为 k×d+k,其中:
- k×d 是权重矩阵 W 的参数数量。
- k 是偏置向量 b 的参数数量。
2)使用 LoRA 微调:
- 需要训练的参数数量为 r×d+k×r+k,其中:
- r×d 是矩阵 A 的参数数量。
- k×r 是矩阵 B 的参数数量。
- k 是偏置向量 b 的参数数量。
3)参数量减少的比例:
-
计算减少比例:
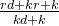
为了简化,我们可以将偏置参数忽略(因为它们相对于权重参数来说数量很小),得到:
≈
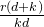
如果假设 k≈d,则有:
≈
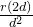 =
=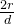
所以,当 k≈d 时,参数减少比例近似为
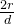 。
。 -
由于 r≪d,所以参数量大幅减少。
2.2.2 举例说明
假设:
- 输入特征维度 d=1024
- 输出特征维度 k=1024
- 低秩值 r=4
1)全量微调参数量:
- 权重参数: 1024×1024=1,048,576
- 偏置参数: 1024
- 总参数量: 1,048,576+1024=1,049,600
2)使用 LoRA 微调参数量:
- 矩阵 A 参数: 4×1024=4,096
- 矩阵 B 参数: 1024×4=4,096
- 偏置参数: 1024
- 总参数量: 4,096+4,096+1024=9,216
3)参数量对比:
- 全量微调: 1,049,600 参数
- LoRA 微调: 9,216 参数
- 参数减少比例: 9,2161,049,600≈0.0088
也就是说,使用 LoRA 后,参数量减少了约 114 倍,即参数量仅为原来的 0.88%。
2.2.3 直观示意图
论文中的这张图直观地展示了这一点:
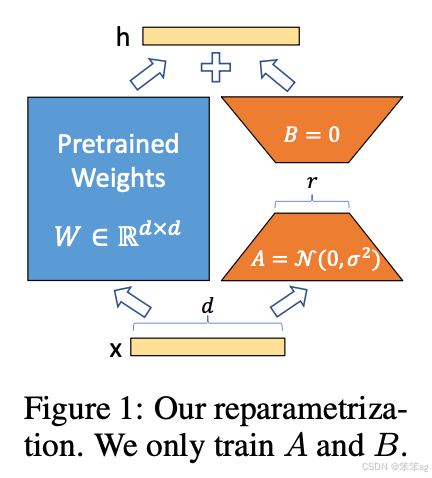
2.3 代码实现:线性层的LoRA
下面我们来实现一个带有 LoRA 的线性层。
- import torch
- import torch.nn as nn
-
- class LoRALinear(nn.Module):
- def __init__(self, in_features, out_features, r):
- super(LoRALinear, self).__init__()
- self.in_features = in_features # 对应 d
- self.out_features = out_features # 对应 k
- self.r = r # 低秩值
-
- # 原始权重矩阵,冻结
- self.weight = nn.Parameter(torch.randn(out_features, in_features))
- self.weight.requires_grad = False # 冻结
-
- # LoRA 部分的参数,初始化 A 为全零,B 从均值为 0 的正态分布中采样
- self.A = nn.Parameter(torch.zeros(r, in_features)) # 形状为 (r, d)
- self.B = nn.Parameter(torch.empty(out_features, r)) # 形状为 (k, r)
- nn.init.normal_(self.B, mean=0.0, std=0.02) # 初始化 B
-
- # 偏置项,可选
- self.bias = nn.Parameter(torch.zeros(out_features))
-
- def forward(self, x):
- # 原始部分
- original_output = torch.nn.functional.linear(x, self.weight, self.bias)
- # LoRA 增量部分
- delta_W = torch.matmul(self.B, self.A) # 形状为 (k, d)
- lora_output = torch.nn.functional.linear(x, delta_W)
- # 总输出
- return original_output + lora_output
在这个实现中,self.weight 是原始的权重矩阵,被冻结不参与训练。self.A 和 self.B 是可训练的低秩矩阵。
3 LoRA在注意力机制中的应用
Transformer 模型的核心是注意力机制,其中涉及到 Query, Key, Value 的计算,这些都是线性变换。
在标准的注意力机制中,计算公式为:
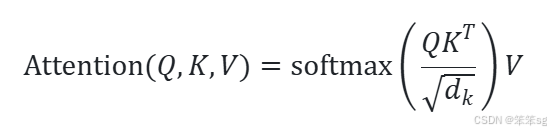
其中 Q, K, V 的计算为:
![]()
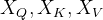 的输入可以相同,也可以不同。例如,在 Cross-Attention 中,解码器的隐藏状态作为
的输入可以相同,也可以不同。例如,在 Cross-Attention 中,解码器的隐藏状态作为 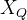 ,编码器的输出作为
,编码器的输出作为 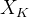 和
和 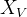 。
。
LoRA 可以应用到 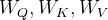 上,采用与线性层类似的方式。
上,采用与线性层类似的方式。
3.1 代码实现:带LoRA的注意力
下面我们实现一个带有 LoRA 的单头注意力层。
- import torch
- import torch.nn as nn
-
- class LoRAAttention(nn.Module):
- def __init__(self, embed_dim, r):
- super(LoRAAttention, self).__init__()
- self.embed_dim = embed_dim # 对应 d_model
- self.r = r # 低秩值
-
- # 原始的 QKV 权重,冻结
- self.W_Q = nn.Linear(embed_dim, embed_dim)
- self.W_K = nn.Linear(embed_dim, embed_dim)
- self.W_V = nn.Linear(embed_dim, embed_dim)
- self.W_O = nn.Linear(embed_dim, embed_dim)
-
- for param in self.W_Q.parameters():
- param.requires_grad = False
- for param in self.W_K.parameters():
- param.requires_grad = False
- for param in self.W_V.parameters():
- param.requires_grad = False
-
- # LoRA 的 Q 部分
- self.A_Q = nn.Parameter(torch.zeros(r, embed_dim))
- self.B_Q = nn.Parameter(torch.empty(embed_dim, r))
- nn.init.normal_(self.B_Q, mean=0.0, std=0.02)
-
- # LoRA 的 K 部分
- self.A_K = nn.Parameter(torch.zeros(r, embed_dim))
- self.B_K = nn.Parameter(torch.empty(embed_dim, r))
- nn.init.normal_(self.B_K, mean=0.0, std=0.02)
-
- # LoRA 的 V 部分
- self.A_V = nn.Parameter(torch.zeros(r, embed_dim))
- self.B_V = nn.Parameter(torch.empty(embed_dim, r))
- nn.init.normal_(self.B_V, mean=0.0, std=0.02)
-
- def forward(self, query, key, value):
- """
- query, key, value: 形状为 (batch_size, seq_length, embed_dim)
- """
- # 计算原始的 Q、K、V
- Q = self.W_Q(query) # (batch_size, seq_length, embed_dim)
- K = self.W_K(key)
- V = self.W_V(value)
-
- # 计算 LoRA 增量部分
- delta_Q = torch.matmul(query, self.A_Q.t()) # (batch_size, seq_length, r)
- delta_Q = torch.matmul(delta_Q, self.B_Q.t()) # (batch_size, seq_length, embed_dim)
- delta_K = torch.matmul(key, self.A_K.t())
- delta_K = torch.matmul(delta_K, self.B_K.t())
- delta_V = torch.matmul(value, self.A_V.t())
- delta_V = torch.matmul(delta_V, self.B_V.t())
-
- # 更新后的 Q、K、V
- Q = Q + delta_Q
- K = K + delta_K
- V = V + delta_V
-
- # 计算注意力得分
- scores = torch.matmul(Q, K.transpose(-2, -1)) / (self.embed_dim ** 0.5)
- attn_weights = torch.nn.functional.softmax(scores, dim=-1)
- context = torch.matmul(attn_weights, V)
-
- # 输出层
- output = self.W_O(context)
-
- return output
代码解释:
- 原始权重:
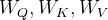 被冻结,不参与训练。
被冻结,不参与训练。 - LoRA 参数:
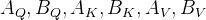 是可训练的低秩矩阵。
是可训练的低秩矩阵。 - 前向传播:
- 首先计算原始的 Q、K、V。
- 然后计算 LoRA 的增量部分,并添加到原始的 Q、K、V 上。
- 接着按照注意力机制进行计算。
4 回到最初的问题:为什么仅导入LoRA模型不能生图?
在理解了 LoRA 的核心思想后,相信你已经可以回答。
原因是:LoRA 模型只是对原始模型的权重更新进行了低秩近似,存储了权重的增量部分 ΔW,而不是完整的模型权重 W。
- LoRA 模型本身不包含原始模型的权重参数,只包含微调时训练的增量参数 A 和 B。
- 在推理(如生成图像)时,必须将 LoRA 的增量参数与原始预训练模型的权重相加,才能得到完整的模型权重。
- 因此,仅仅加载 LoRA 模型是无法进行推理的,必须结合原始的预训练模型一起使用。
打个比方,LoRA 模型就像是给一幅画添加的“修改指令”,但这些指令需要在原始画作的基础上才能生效。如果你只有修改指令(LoRA 模型),却没有原始的画作(预训练模型),那么你就无法得到最终的作品。
所以,要使用 LoRA 模型生成图像,必须同时加载预训练的基础模型和对应的 LoRA 模型。
5 总结
LoRA 通过将权重更新分解为两个低秩矩阵 A 和 B 的乘积,极大地减少了微调过程中需要训练的参数量。在性能几乎不受影响的情况下,显著降低了计算资源的需求,使得在资源受限的环境中微调大型预训练模型成为可能。
这真的是一个很理所当然的想法,不由得感叹数学的重要性。
6 推荐阅读
题外话:LoRA 的灵感其实涉及到了线性代数的知识,对于想深入学习线性代数的同学们,推荐一本很好的自学教材:《线性代数及其应用》,作者是 David C. Lay、Steven R. Lay 和 Judi J. McDonald,英文名为:《Linear Algebra and Its Applications》。

评论记录:
回复评论: