矩阵的特征分解非常好理解,假设现在有一个NxN的矩阵A,如果这个矩阵A有N个线性无关的特征向量,那么A就可以分解为
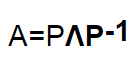
P代表NxN的方阵,中间的Λ 代表对角矩阵
怎么理解呢?为什么可以分解成这样呢?
其实这个就是矩阵相似对角化的变形而已!
我们首先来复习一下矩阵相似对角化的基本概念
对角矩阵 : 对角矩阵是指只有主对角线上含有非零元素的矩阵,一般记作:Λ ,例如:
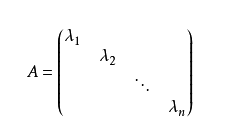
矩阵相似:若矩阵A和矩阵B都是n阶矩阵,如果存在可逆矩阵P,使得:
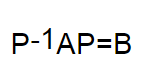
则称矩阵A和B相似,记作A~B
矩阵相似对角化:如果一个n阶矩阵A有n个线性无关的特征向量,那么矩阵A与由其特征值所组成的对角矩阵相似,即:
A~Λ
所以现在我们再回来看特征分解的意思
1.有一个NxN的矩阵A (说明这个矩阵是一个方阵)
2.这个矩阵A有N个线性无关的特征向量 (说明这个矩阵A可以相似对角化)
所以有:
A~Λ
由矩阵相似的定义有:

把左边的P变换到右边去,则有
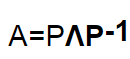

评论记录:
回复评论: