梯度下降
梯度下降(Gradient Descent)是一种在机器学习和深度学习中广泛使用的优化算法,用于最小化给定的目标函数。目标函数通常表示模型的误差或损失,我们的目标是找到一组参数,使得这个误差尽可能小。
梯度下降的基本思想是迭代地调整模型参数,以减小目标函数的值。它基于这样的观察:如果函数 F(θ)在点 θ是可微的,那么 F(θ)在该点的梯度(∇F(θ)指向函数增长最快的方向。因此,如果我们从当前位置沿着梯度的反方向移动一小步,我们就可以降低函数的值。
以下是梯度下降的一般步骤:
- 初始化参数:首先随机选择一个起始点作为参数的初始值。
- 计算梯度:计算目标函数相对于参数的梯度。梯度是一个向量,它的每个分量对应于目标函数对相应参数的偏导数。
- 更新参数:根据以下公式更新参数:θ:=θ−η⋅∇F(θ) 其中,θ表示参数向量,η 称为学习率(learning rate),是一个正标量,决定了我们在梯度方向上迈出的步伐大小。
- 重复步骤2和3:直到满足停止条件(例如,达到最大迭代次数、梯度足够小或者目标函数的变化足够小)。
梯度下降有几种变体,包括:
- 批量梯度下降(Batch Gradient Descent):每次迭代使用整个训练集来计算梯度。这种方法能保证每次迭代都朝着全局最优解前进,但当数据集非常大时,计算成本非常高。
- 随机梯度下降(Stochastic Gradient Descent, SGD):每次迭代只使用一个样本(或极小批次)来估计梯度。这大大加快了每一步的速度,但路径可能更加波动。
- 小批量梯度下降(Mini-batch Gradient Descent):这是批量梯度下降和随机梯度下降的一种折衷,它使用一个小批量的数据样本来计算梯度。这种方式既保持了一定程度上的计算效率,又能减少随机性带来的波动。
此外,还有许多改进版本的梯度下降算法,比如动量梯度下降、Adagrad、RMSprop、Adam等,它们通过不同的策略调整学习率或者结合历史梯度信息来加速收敛或改善性能。
1、无约束最优化问题
1.1、无约束最优化
无约束最优化问题(unconstrained optimization problem)指的是从一个问题的所有可能的备选方案中,选择出依某种指标来说是最优的解决方案。从数学上说,最优化是研究在一个给定的集合S上泛函 J ( θ ) J(\theta) J(θ)的极小化或极大化问题:广义上,最优化包括数学规划、图和网络、组合最优化、库存论、决策论、排队论、最优控制等。狭义上,最优化仅指数学规划。
1.2、梯度下降
梯度下降法(Gradient Descent)是一个算法,但不是像多元线性回归那样是一个具体做回归任务的算法,而是一个非常通用的优化算法来帮助一些机器学习算法(都是无约束最优化问题)求解出最优解, 所谓的通用就是很多机器学习算法都是用梯度下降,甚至深度学习也是用它来求解最优解。所有优化算法的目的都是期望以最快的速度把模型参数θ求解出来,梯度下降法就是一种经典常用的优化算法。
之前利用正规方程求解的 θ 是最优解的原因是 MSE 这个损失函数是凸函数。但是,机器学习的损失函数并非都是凸函数,设置导数为 0 会得到很多个极值,不能确定唯一解。
使用正规方程 θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy 求解的另一个限制是特征维度( X 1 、 X 2 … … 、 X n X_1、X_2……、X_n X1、X2……、Xn)不能太多,矩阵逆运算的时间复杂度通常为 O ( n 3 ) O(n^3) O(n3) 。换句话说,就是如果特征数量翻$ 2$倍,你的计算时间大致为原来的倍,也就是之前时间的8倍。举个例子,2 个特征 1 秒,4 个特征就是 8 秒,8 个特征就是 64 秒,16 个特征就是 512 秒,当特征更多的时候呢?运行时间会非常漫长~
所以正规方程求出最优解并不是机器学习甚至深度学习常用的手段。
之前我们令导数为 0,反过来求解最低点 θ 是多少,而梯度下降法是一点点去逼近最优解!
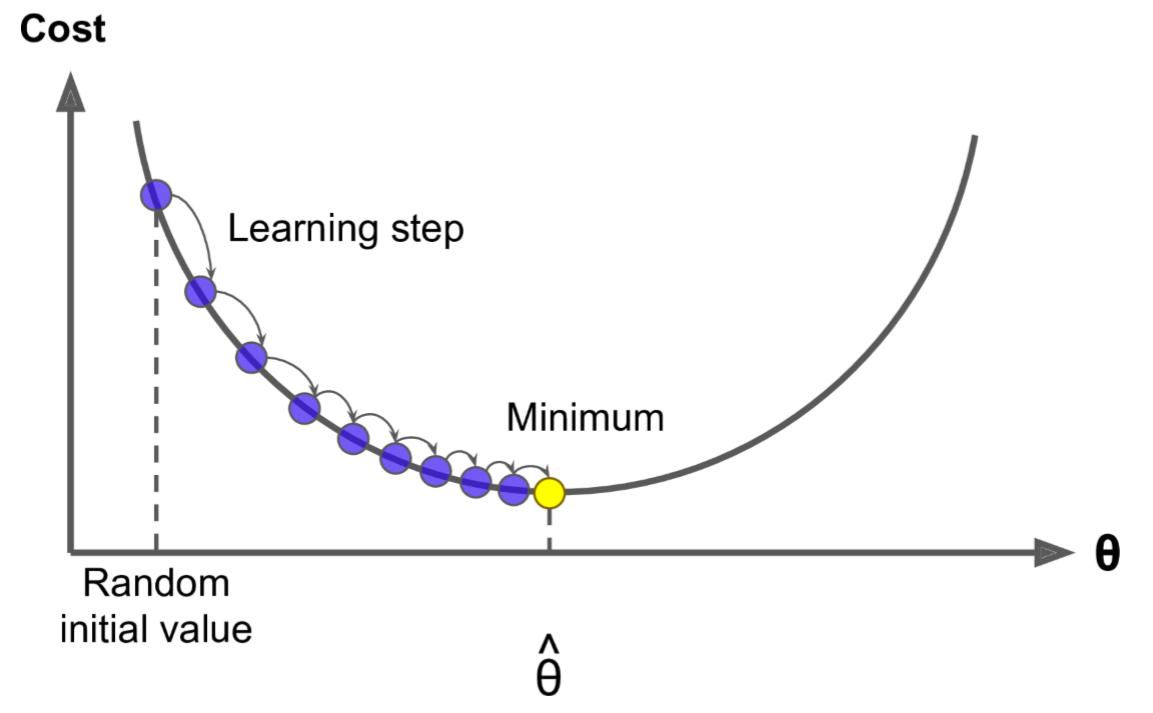
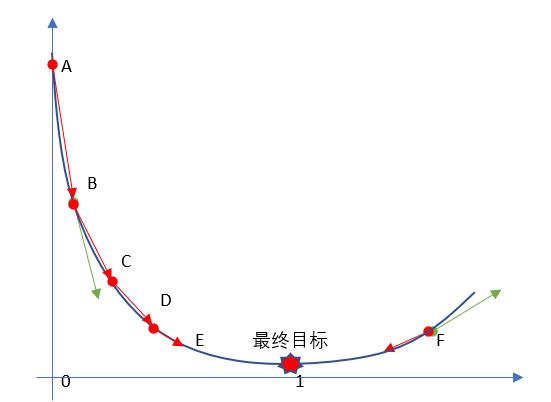
其实这就跟生活中的情形很像,比如你问一个朋友的工资是多少,他说你猜?那就很难了,他说你猜完我告诉你是猜高了还是猜低了,这样你就可以奔着对的方向一直猜下去,最后总会猜对!梯度下降法就是这样的,多次尝试。并且,在试的过程中还得想办法知道是不是在猜对的路上,说白了就是得到正确的反馈再调整然后继续猜才有意义~
这个就好比道士下山,我们把 Loss (或者称为Cost,即损失)曲线看成是山谷,如果走过了,就再 往回返,所以是一个迭代的过程。
1.3、梯度下降公式
这里梯度下降法的公式就是一个式子指导计算机迭代过程中如何去调整 θ \theta θ,可以通过行泰勒公式一阶展开来进推导和证明:

这里的 w j w_j wj 就是 θ \theta θ 中的某一个 j = 0…m,这里的 η \eta η 就是梯度下降图里的 learning step,很多时候也叫学习率 learning rate,很多时候也用 α \alpha α 表示,这个学习率我们可以看作是下山迈的步子的大小,步子迈的大下山就快。
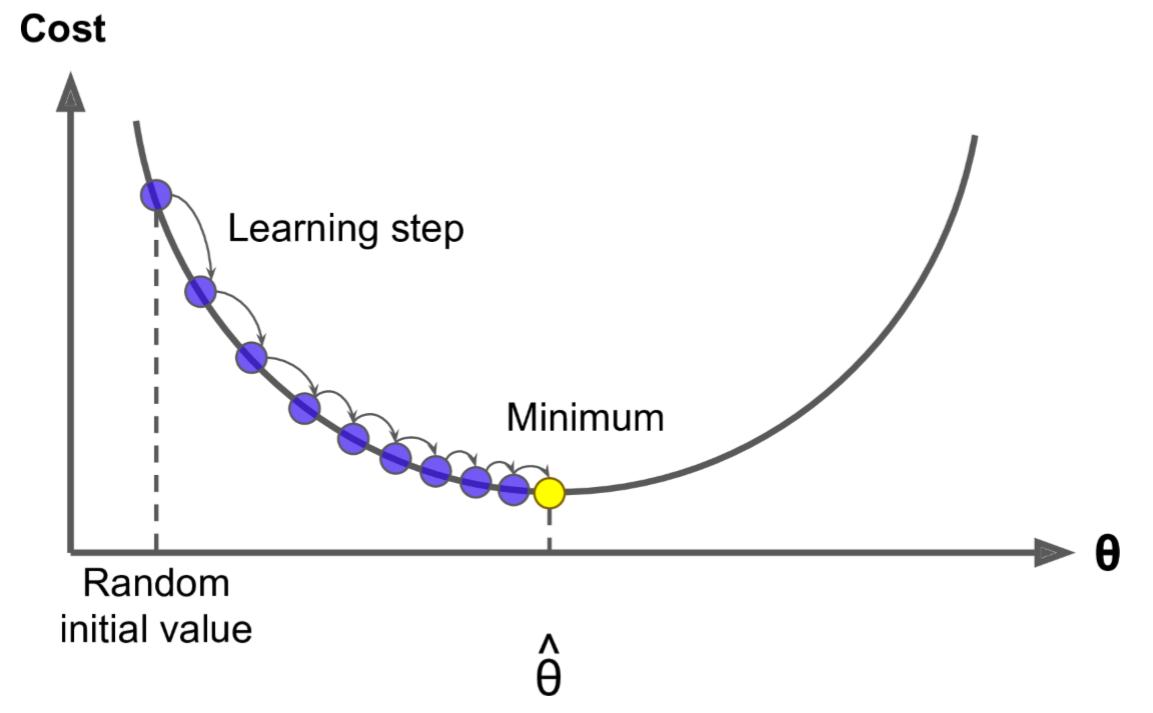
学习率一般都是正数,如果在山左侧(曲线左半边)梯度是负的,那么这个负号就会把 w j w_j wj 往大了调, 如果在山右侧(曲线右半边)梯度就是正的,那么负号就会把 w j w_j wj 往小了调。每次 w j w_j wj 调整的幅度就是 η ∗ g r a d i e n t \eta * gradient η∗gradient,就是横轴上移动的距离。
因此,无论在左边,还是在右边,梯度下降都可以快速找到最优解,实现快速下山~
如果特征或维度越多,那么这个公式用的次数就越多,也就是每次迭代要应用的这个式子多次(多少特征,就应用多少次),所以其实上面的图不是特别准,因为 θ \theta θ 对应的是很多维度,应该每一个维度都可以画一个这样的图,或者是一个多维空间的图。
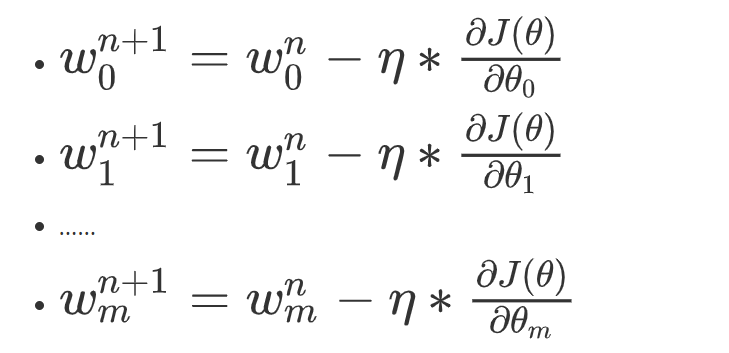
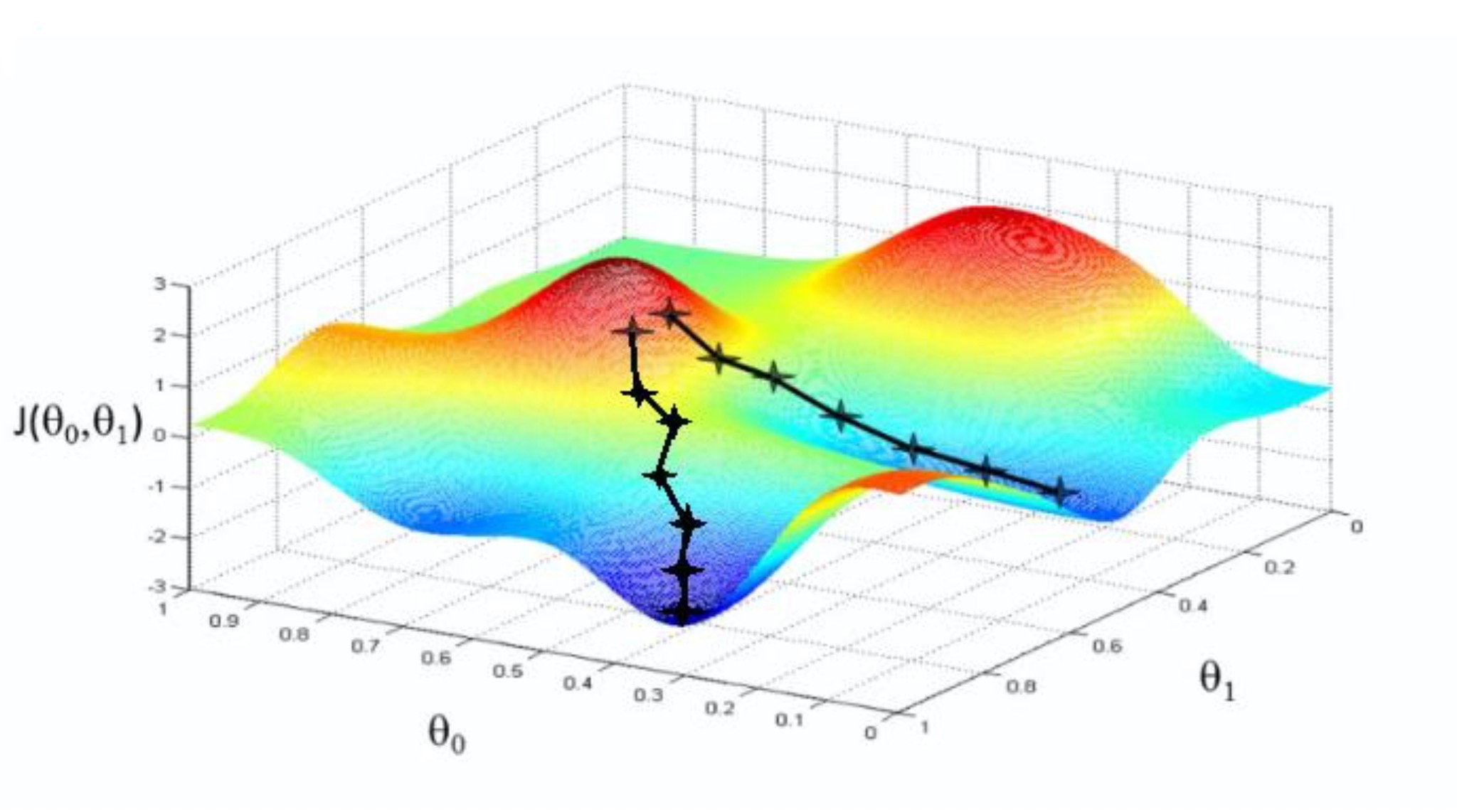
所以观察上图我们可以发现不是某一个 θ 0 \theta_0 θ0 或 θ 1 \theta_1 θ1 找到最小值就是最优解,而是它们一起找到 J ( θ ) J(\theta) J(θ) 最小值才是最优解。
1.4、学习率
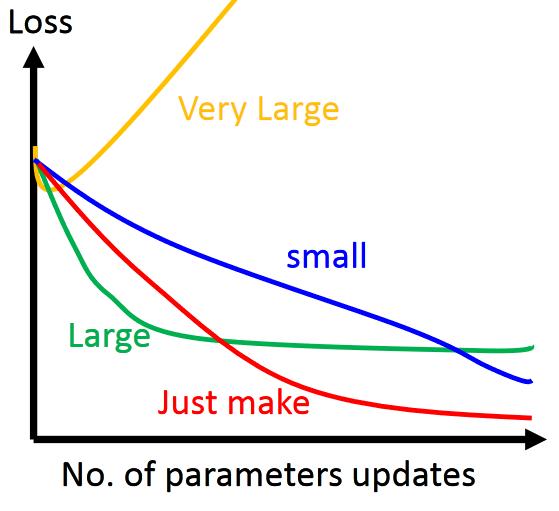
根据我们上面讲的梯度下降公式,我们知道 η \eta η 是学习率,设置大的学习率 w j w_j wj 每次调整的幅度就大,设置小的学习率 w j w_j wj 每次调整的幅度就小,然而如果步子迈的太大也会有问题,俗话说步子大了容易扯着蛋!学习率大,可能一下子迈过了,到另一边去了(从曲线左半边跳到右半边),继续梯度下降又迈回来, 使得来来回回震荡。步子太小呢,就像蜗牛一步步往前挪,也会使得整体迭代次数增加。
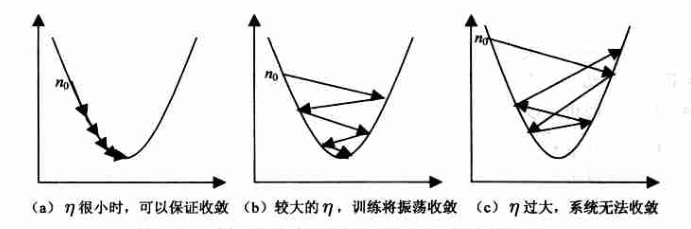
学习率的设置是门一门学问,一般我们会把它设置成一个比较小的正整数,0.1、0.01、0.001、0.0001,都是常见的设定数值(然后根据情况调整)。一般情况下学习率在整体迭代过程中是不变,但是也可以设置成随着迭代次数增多学习率逐渐变小,因为越靠近山谷我们就可以步子迈小点,可以更精准的走入最低点,同时防止走过。还有一些深度学习的优化算法会自己控制调整学习率这个值,后面学习过程中这些策略在讲解代码中我们会一一讲到。
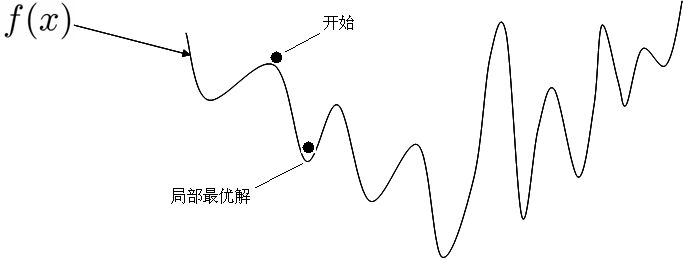
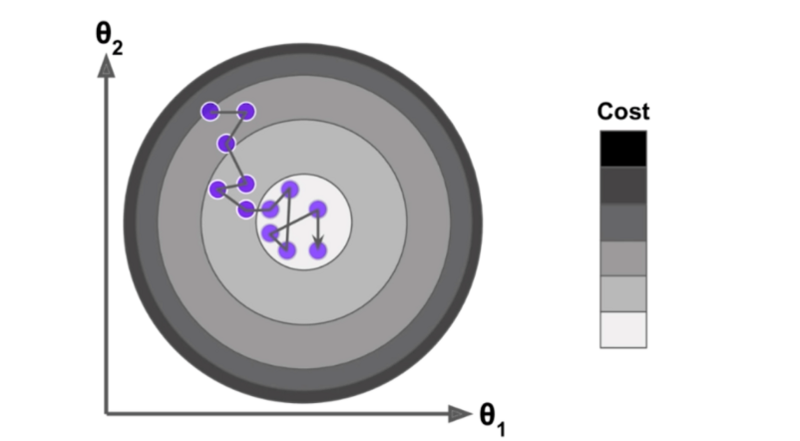
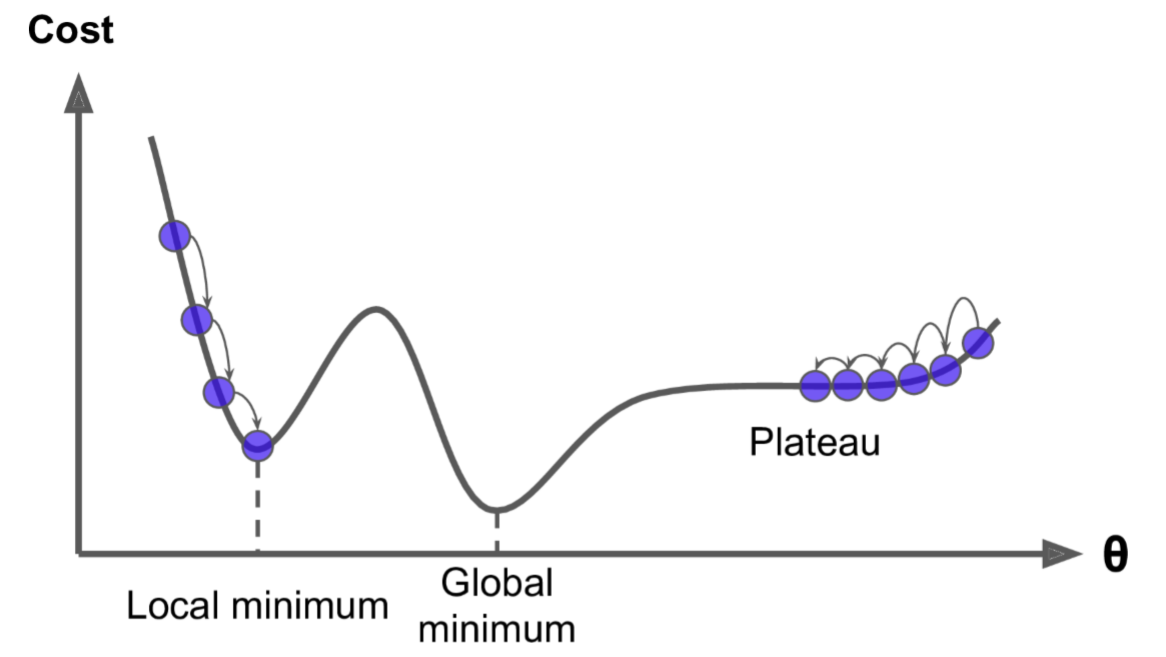
1.5、全局最优化
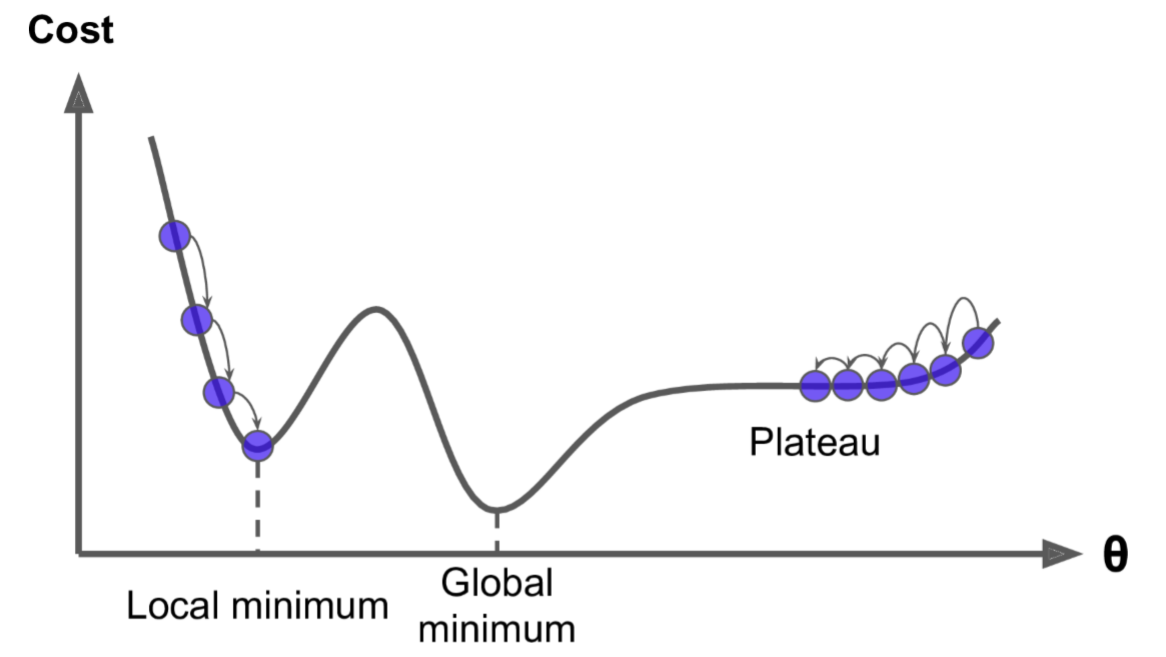
上图显示了梯度下降的两个主要挑战:
- 若随机初始化,算法从左侧起步,那么会收敛到一个局部最小值,而不是全局最小值;
- 若随机初始化,算法从右侧起步,那么需要经过很长时间才能越过Plateau(函数停滞带,梯度很小),如果停下得太早,则永远达不到全局最小值;
而线性回归的模型MSE损失函数恰好是个凸函数,凸函数保证了只有一个全局最小值,其次是个连续函数,斜率不会发生陡峭的变化,因此即便是乱走,梯度下降都可以趋近全局最小值。
上图损失函数是非凸函数,梯度下降法是有可能落到局部最小值的,所以其实步长不能设置的太小太稳健,那样就很容易落入局部最优解,虽说局部最小值也没大问题, 因为模型只要是堪用的就好嘛,但是我们肯定还是尽量要奔着全局最优解去!
1.6、梯度下降步骤
梯度下降流程就是“猜”正确答案的过程:
-
1、“瞎蒙”,Random 随机数生成 θ \theta θ,随机生成一组数值 w 0 、 w 1 … … w n w_0、w_1……w_n w0、w1……wn ,期望 μ \mu μ 为 0 方差 σ \sigma σ 为 1 的正太分布数据。
-
2、求梯度 g ,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降
-
3、if g < 0, θ \theta θ 变大,if g > 0, θ \theta θ 变小
-
4、判断是否收敛,如果收敛跳出迭代,如果没有达到收敛,回第 2 步再次执行2~4步
收敛的判断标准是:随着迭代进行损失函数Loss,变化非常微小甚至不再改变,即认为达到收敛
1.7、代码模拟梯度下降
-
梯度下降优化算法,比正规方程,应用更加广泛
-
什么是梯度?
- 梯度就是导数对应的值!
-
下降?
- 涉及到优化问题,最小二乘法
-
梯度下降呢?
- 梯度方向下降,速度最快的~
接下来,我们使用代码来描述上面梯度下降的过程:
方程如下:
f ( x ) = ( x − 3.5 ) 2 − 4.5 x + 10 f(x) = (x - 3.5)^2 - 4.5x + 10 f(x)=(x−3.5)2−4.5x+10
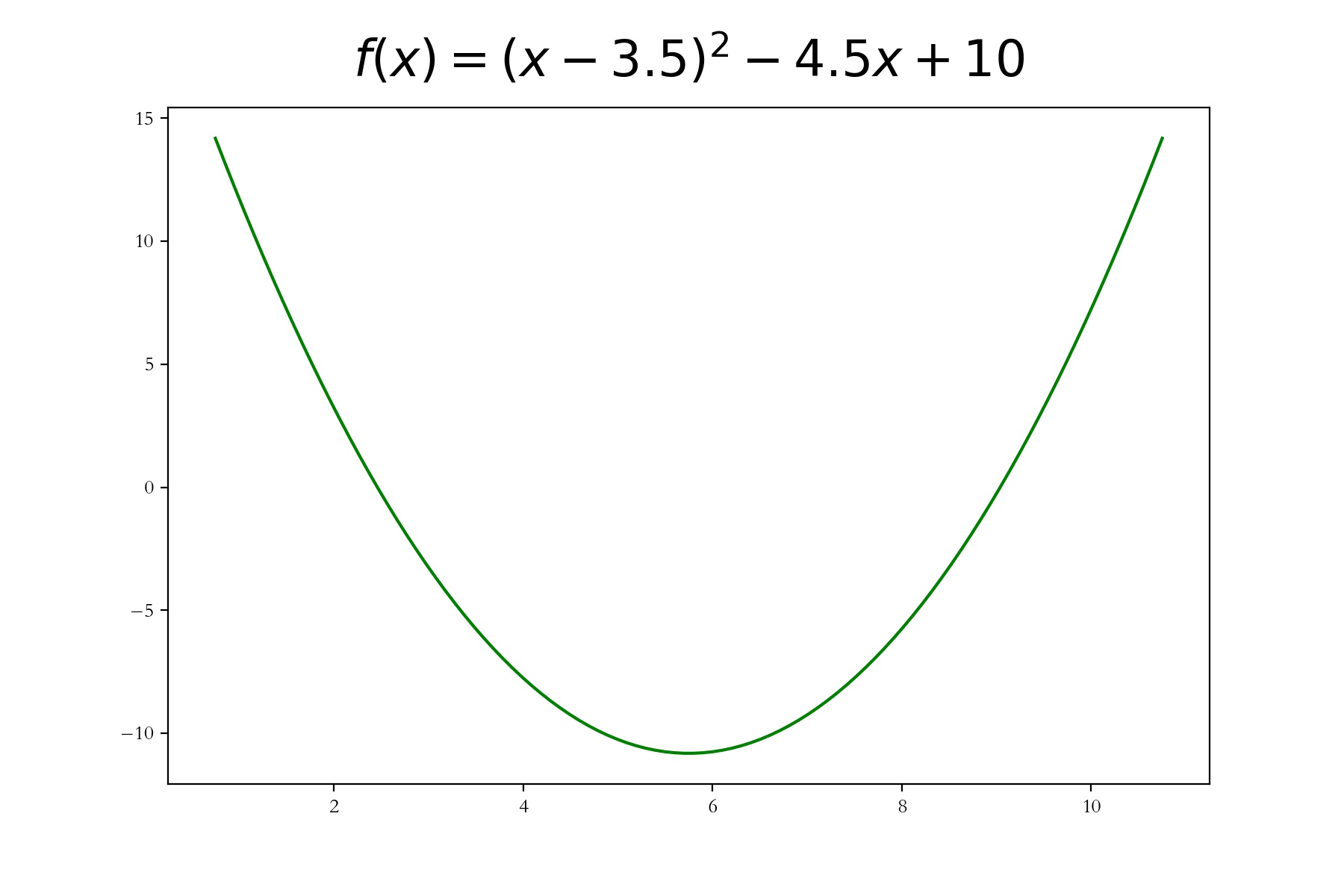
使用梯度下降的思想,来一步步逼近,函数的最小值。
import numpy as np
import matplotlib.pyplot as plt
f = lambda x : (x - 3.5)**2 -4.5*x + 10
# 导函数
d = lambda x :2*(x - 3.5) - 4.5 # 梯度 == 导数
# 梯度下降的步幅,比例,(学习率,幅度)
step = 0.1
# 求解当x等于多少的时候,函数值最小。求解目标值:随机生成的
# 相等于:'瞎蒙' ----> 方法 ----> 优化
x = np.random.randint(0,12,size = 1)[0]
# 梯度下降,每下降一步,每走一步,目标值,都会更新。
# 更新的这个新值和上一步的值,差异,如果差异很小(万分之一)
# 梯度下降退出
last_x = x + 0.02 # 记录上一步的值,首先让last_x和x有一定的差异!!!
# 精确率,真实计算,都是有误差,自己定义
precision = 1e-4
print('+++++++++++++++++++++', x)
x_ = [x]
while True:
# 退出条件,精确度,满足了
if np.abs(x - last_x) < precision:
break
# 更新
last_x = x
x -= step*d(x) # 更新,减法:最小值
x_.append(x)
print('--------------------',x)
# 数据可视化
plt.rcParams['font.family'] = 'Kaiti SC'
plt.figure(figsize=(9,6))
x = np.linspace(5.75 - 5, 5.75 + 5, 100)
y = f(x)
plt.plot(x,y,color = 'green')
plt.title('梯度下降',size = 24,pad = 15)
x_ = np.array(x_)
y_ = f(x_)
plt.scatter(x_, y_,color = 'red')
plt.savefig('./图片/5-梯度下降.jpg',dpi = 200)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
函数的最优解是:5.75。你可以发现,随机赋值的变量 x ,无论大于5.75,还是小于5.75,经过梯度下降,最终都慢慢靠近5.75这个最优解!
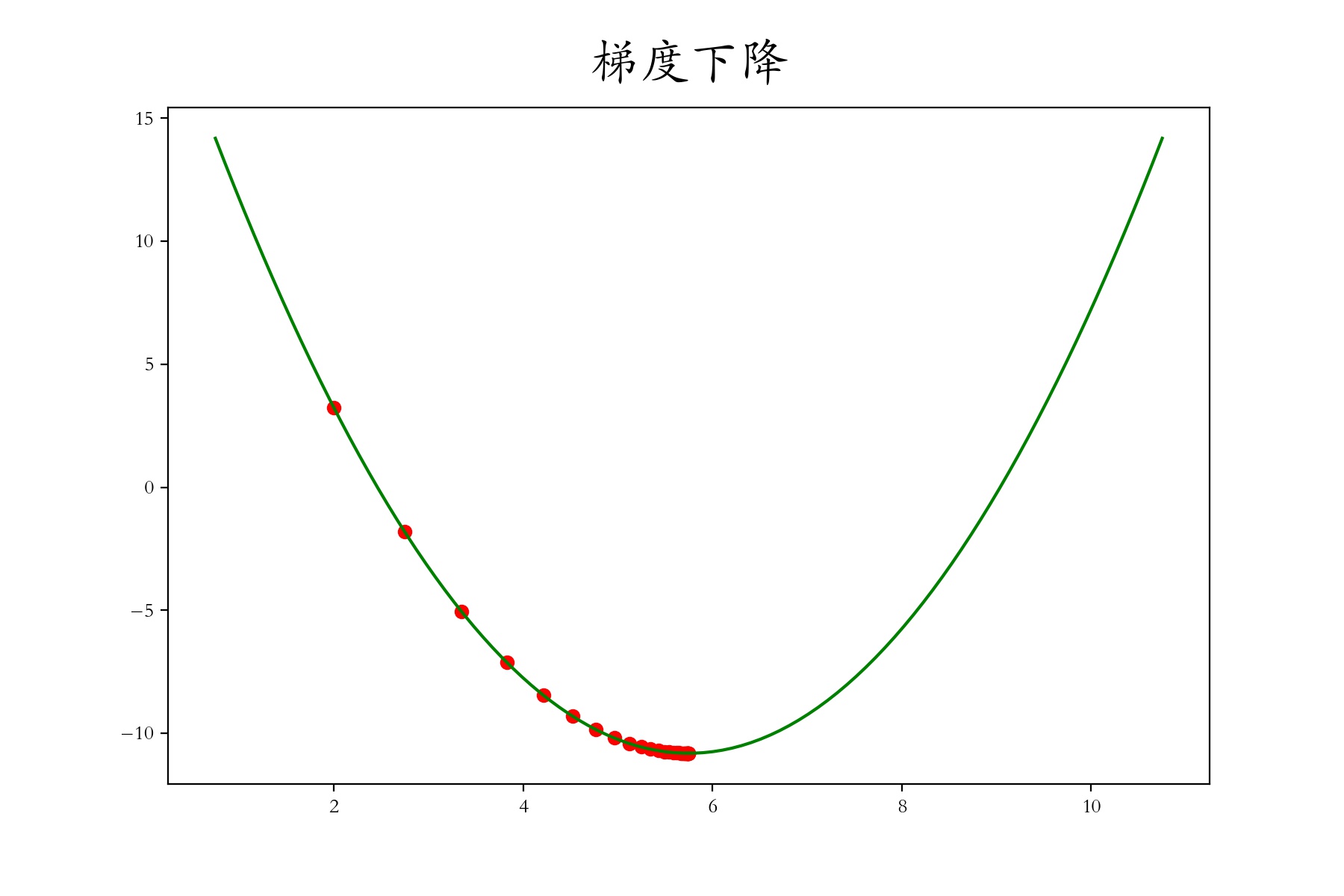
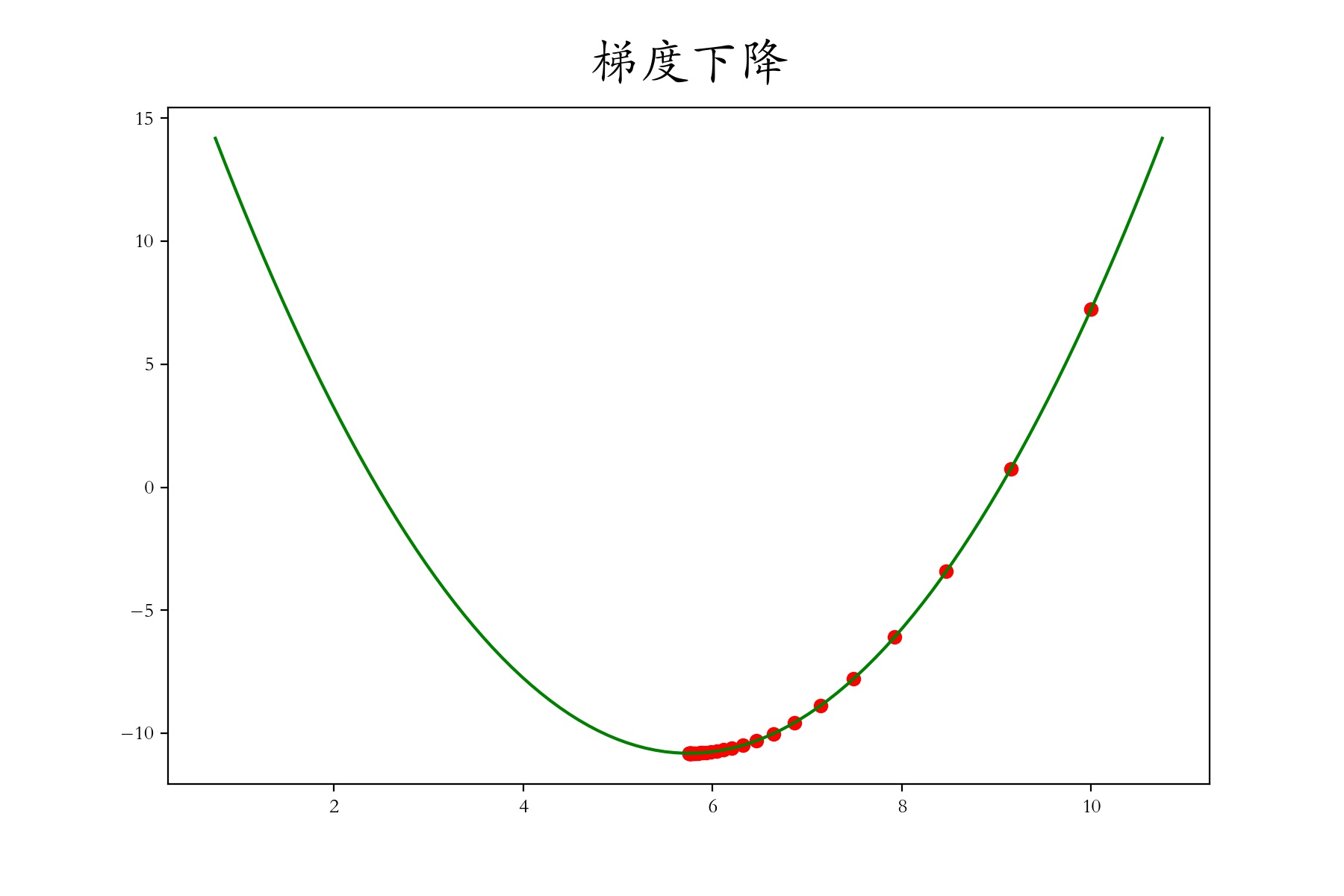
注意:
- 梯度下降存在一定误差,不是完美解~
- 在误差允许的范围内,梯度下降所求得的机器学习模型,是堪用的!
- 梯度下降的步幅step,不能太大,俗话说步子不能迈的太大!
- 精确度,可以根据实际情况调整
- while True循环里面,持续进行梯度下降:
θ = θ − η ∂ ∂ θ J ( θ ) \theta = \theta - \eta \frac{\partial}{\partial \theta}J(\theta) θ=θ−η∂θ∂J(θ) 其中的 $\eta $ 叫做学习率
x = x − η ∂ ∂ x f ( x ) x = x - \eta\frac{\partial}{\partial x}f(x) x=x−η∂x∂f(x)
x = x − s t e p ∗ ∂ ∂ x f ( x ) x = x - step*\frac{\partial}{\partial x} f(x) x=x−step∗∂x∂f(x) 其中的 $step $ 叫做学习率
x = x − s t e p ∗ f ′ ( x ) x = x - step * f'(x) x=x−step∗f′(x)
- while 循环退出条件是:x更新之后和上一次相差绝对值小于特定精确度!
2、梯度下降方法
2.1、三种梯度下降不同
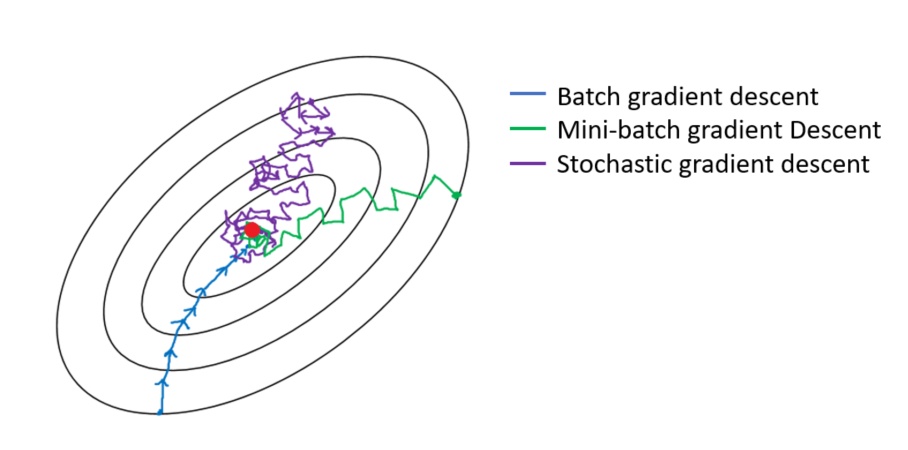
梯度下降分三类:批量梯度下降BGD(Batch Gradient Descent)、小批量梯度下降MBGD(Mini-Batch Gradient Descent)、随机梯度下降SGD(Stochastic Gradient Descent)。
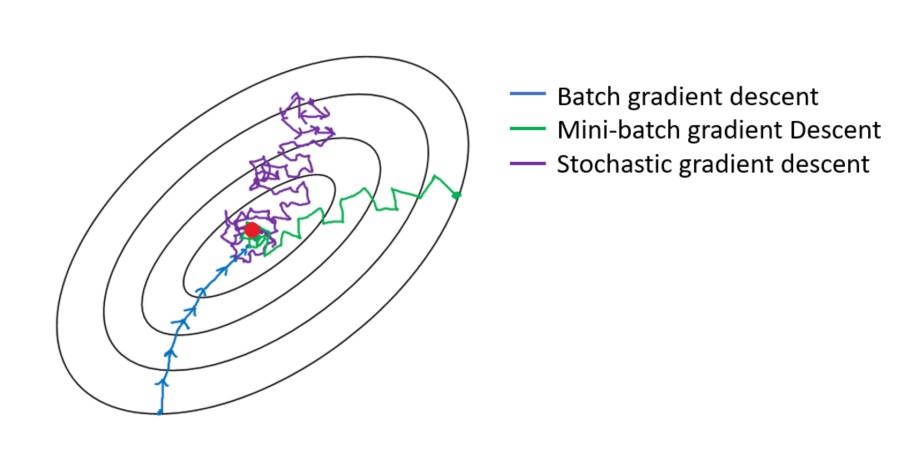
三种梯度下降有什么不同呢?我们从梯度下降步骤开始讲起,梯度下降步骤分一下四步:
-
1、随机赋值,Random 随机数生成 θ \theta θ,随机一组数值 w 0 、 w 1 … … w n w_0、w_1……w_n w0、w1……wn
-
2、求梯度 g ,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降
-
3、if g < 0, θ \theta θ 变大,if g > 0, θ \theta θ 变小
-
4、判断是否收敛 convergence,如果收敛跳出迭代,如果没有达到收敛,回第 2 步再次执行2~4步
收敛的判断标准是:随着迭代进行损失函数Loss,变化非常微小甚至不再改变,即认为达到收敛
三种梯度下降不同,体现在第二步中:
- BGD是指在每次迭代使用所有样本来进行梯度的更新
- MBGD是指在每次迭代使用一部分样本(所有样本500个,使用其中32个样本)来进行梯度的更新
- SGD是指每次迭代随机选择一个样本来进行梯度更新
2.2、线性回归梯度更新公式
回顾上一讲公式!
最小二乘法公式如下:
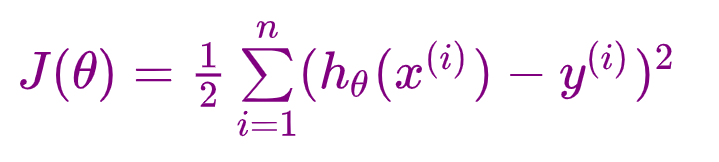
矩阵写法:
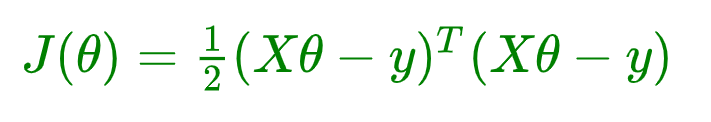
接着我们来讲解如何求解上面梯度下降的第 2 步,即我们要推导出损失函数的导函数来。
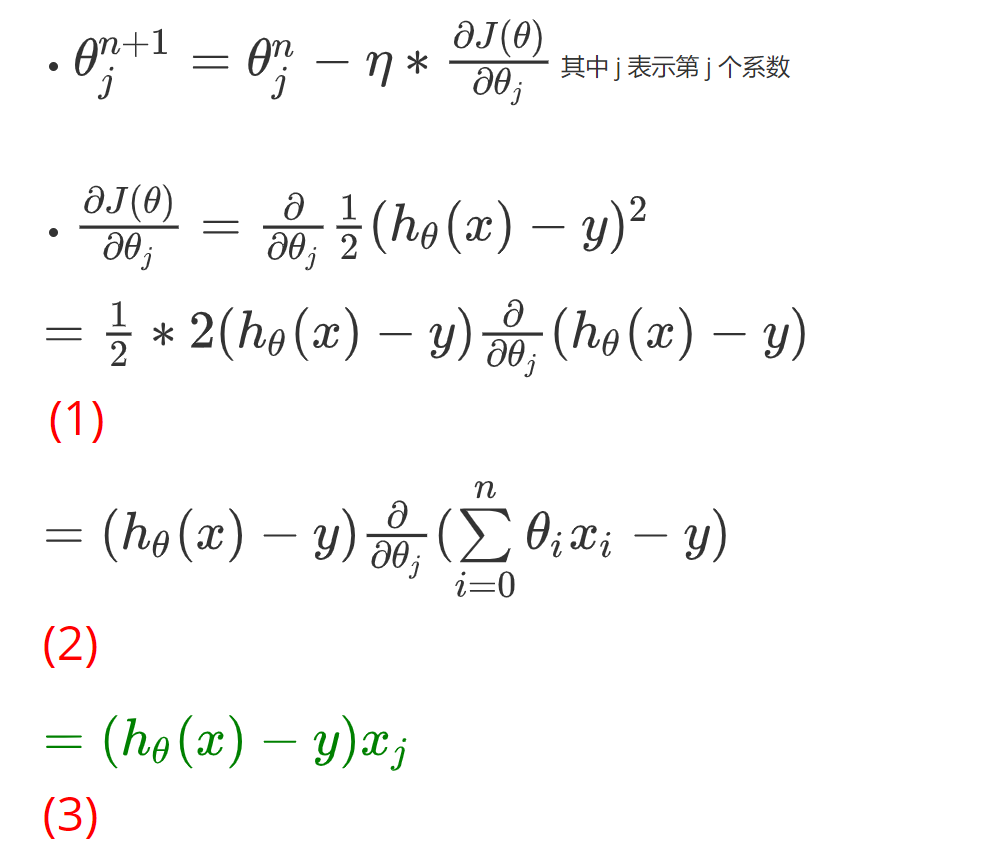
x 2 x^2 x2的导数就是 2x,根据链式求导法则,我们可以推出上面第(1)步。然后是多元线性回归,所以 h θ ( x ) h_{\theta}(x) hθ(x) 就 是 θ T x \theta^Tx θTx 即是 w 0 x 0 + w 1 x 1 + … … + w n x n w_0x_0 + w_1x_1 + …… + w_nx_n w0x0+w1x1+……+wnxn 即 ∑ i = 0 n θ i x i \sum\limits_{i = 0}^n\theta_ix_i i=0∑nθixi。到这里我们是对 θ j \theta_j θj 来求偏导,那么和 w j w_j wj 没有关系的可以忽略不计,所以只剩下 x j x_j xj。
我们可以得到结论就是 θ j \theta_j θj 对应的梯度与预测值 y ^ \hat{y} y^ 和真实值 y 有关,这里 y ^ \hat{y} y^ 和 y 是列向量(即多个数据),同时还与 θ j \theta_j θj 对应的特征维度 x j x_j xj 有关,这里 x j x_j xj 是原始数据集矩阵的第 j 列。如果我们分别去对每个维度 θ 0 、 θ 1 … … θ n \theta_0、\theta_1……\theta_n θ0、θ1……θn 求偏导,即可得到所有维度对应的梯度值。
- g 0 = ( h θ ( x ) − y ) x 0 g_0 = (h_{\theta}(x) - y)x_0 g0=(hθ(x)−y)x0
- g 1 = ( h θ ( x ) − y ) x 1 g_1 = (h_{\theta}(x) - y)x_1 g1=(hθ(x)−y)x1
- ……
- g j = ( h θ ( x ) − y ) x j g_j = (h_{\theta}(x) - y)x_j gj=(hθ(x)−y)xj
总结:
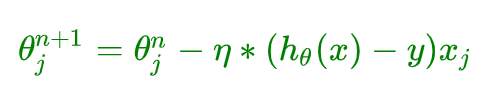
2.3、批量梯度下降BGD
批量梯度下降法是最原始的形式,它是指在每次迭代使用所有样本来进行梯度的更新。每次迭代参数更新公式如下:
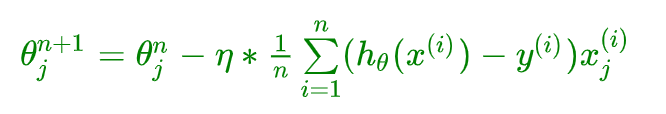
去掉 1 n \frac{1}{n} n1 也可以,因为它是一个常量,可以和 η \eta η 合并
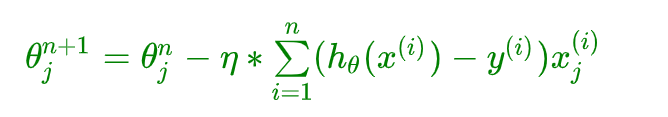
矩阵写法:
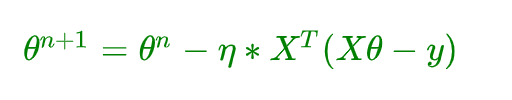
其中 ? = 1, 2, …, n 表示样本数, ? = 0, 1……表示特征数,这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。
注意这里更新时存在一个求和函数,即为对所有样本进行计算处理!
优点:
(1)一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
(2)由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点:
(1)当样本数目 n 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。
从迭代的次数上来看,BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:
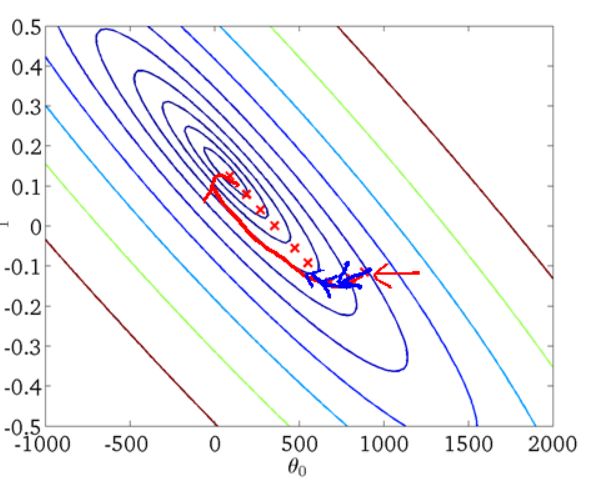
2.4、随机梯度下降SGD
随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。每次迭代参数更新公式如下:
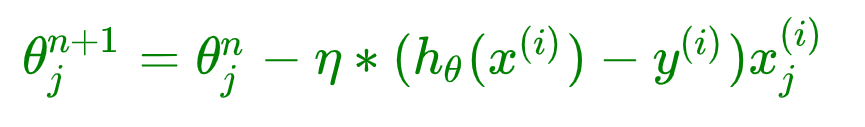
批量梯度下降算法每次都会使用全部训练样本,因此这些计算是冗余的,因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数,因此每次的学习是非常快速的。
优点:
(1)由于不是在全部训练数据上的更新计算,而是在每轮迭代中,随机选择一条数据进行更新计算,这样每一轮参数的更新速度大大加快。
缺点:
(1)准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
(2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
解释一下为什么SGD收敛速度比BGD要快:
* 这里我们假设有30W个样本,对于BGD而言,每次迭代需要计算30W个样本才能对参数进行一次更新,需要求得最小值可能需要多次迭代(假设这里是10)。
* 而对于SGD,每次更新参数只需要一个样本,因此若使用这30W个样本进行参数更新,则参数会被迭代30W次,而这期间,SGD就能保证能够收敛到一个合适的最小值上了。
* 也就是说,在收敛时,BGD计算了 10×30W 次,而SGD只计算了 1×30W 次。
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程就会盲目一些。其迭代的收敛曲线示意图可以表示如下:
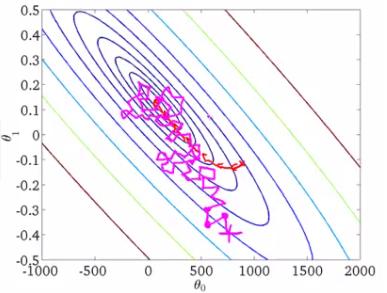
2.5、小批量梯度下降MBGD
小批量梯度下降,是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是:每次迭代使用总样本中的一部分(batch_size)样本来对参数进行更新。这里我们假设 batch_size = 32,样本数 n = 1000 。实现了更新速度与更新次数之间的平衡。每次迭代参数更新公式如下:
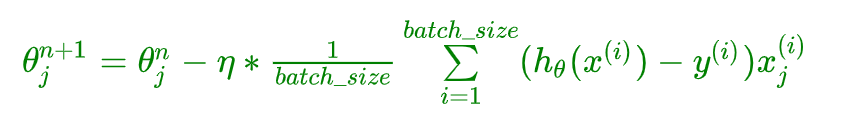
相对于随机梯度下降算法,小批量梯度下降算法降低了收敛波动性, 即降低了参数更新的方差,使得更新更加稳定。相对于全量梯度下降,其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。
一般情况下,小批量梯度下降是梯度下降的推荐变体,特别是在深度学习中。每次随机选择2的幂数个样本来进行学习,例如:8、16、32、64、128、256。因为计算机的结构就是二进制的。但是也要根据具体问题而选择,实践中可以进行多次试验, 选择一个更新速度与更次次数都较适合的样本数。
MBGD梯度下降迭代的收敛曲线更加温柔一些:
2.6、梯度下降优化
虽然梯度下降算法效果很好,并且广泛使用,但是不管用上面三种哪一种,都存在一些挑战与问题,我们可以从以下几点进行优化:
-
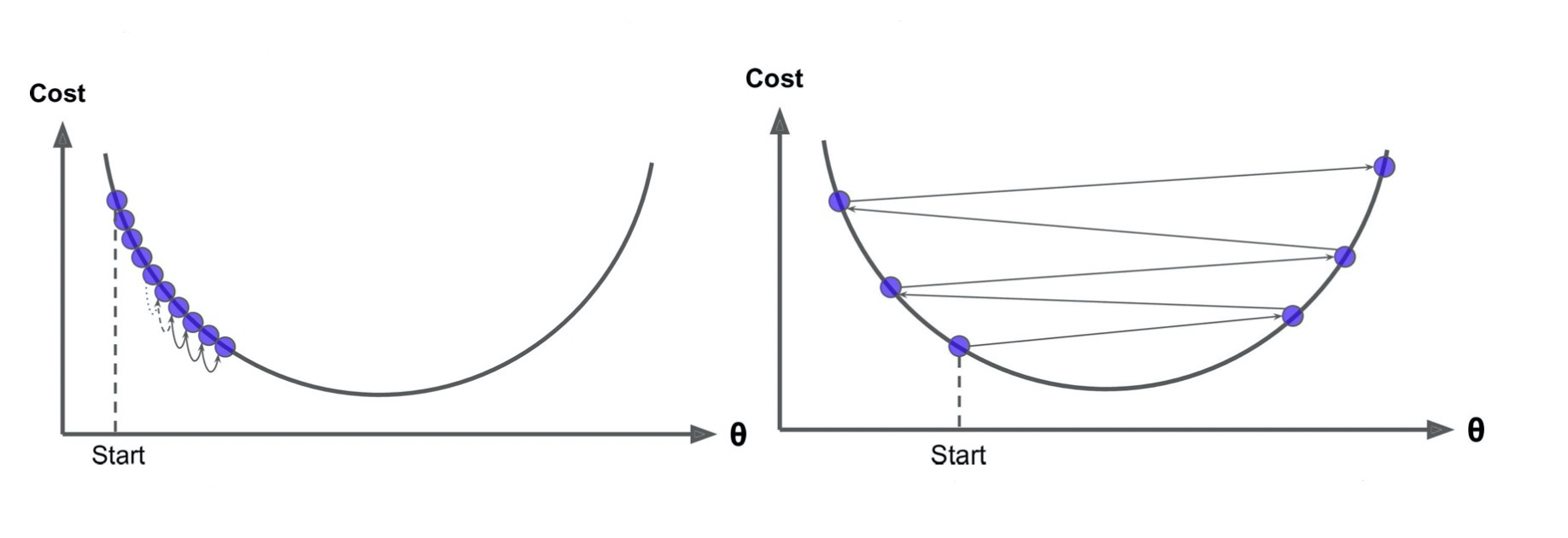
选择一个合理的学习速率很难。如果学习速率过小,则会导致收敛速度很慢。如果学习速率过大,那么其会阻碍收敛,即在极值点附近会振荡。
-
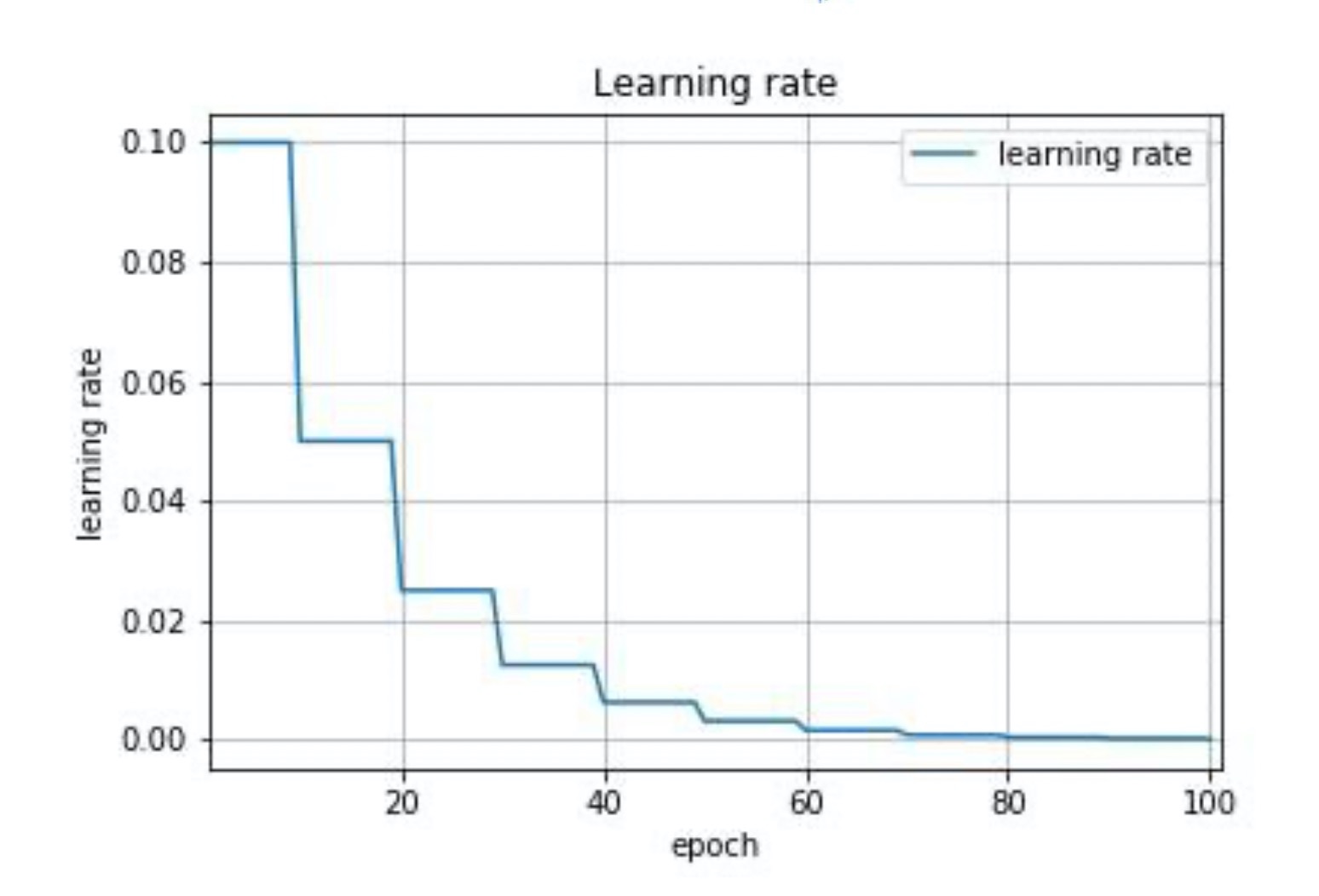
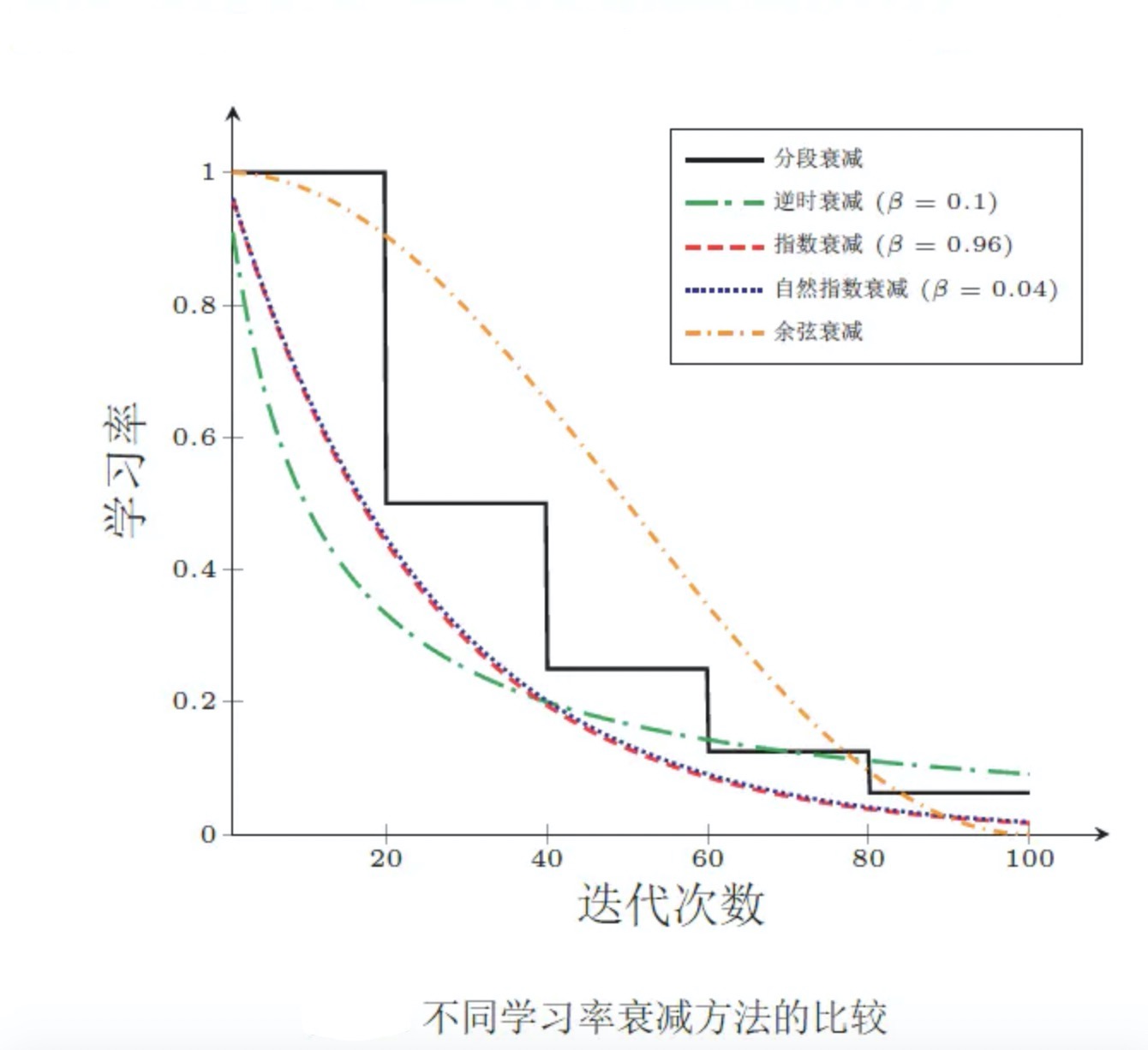
学习速率调整,试图在每次更新过程中, 改变学习速率。从经验上看,**学习率在一开始要保持大些来保证收敛速度,在收敛到最优点附近时要小些以避免来回震荡。**比较简单的学习率调整可以通过 **学习率衰减(Learning Rate Decay)**的方式来实现。假设初始化学习率为 η 0 \eta_0 η0,在第 t 次迭代时的学习率 η t \eta_t ηt。常用的衰减方式为可以设置为 按迭代次数 进行衰减,迭代次数越大,学习率越小!
-
模型所有的参数每次更新都是使用相同的学习速率。如果数据特征是稀疏的,或者每个特征有着不同的统计特征与空间,那么便不能在每次更新中每个参数使用相同的学习速率,那些很少出现的特征应该使用一个相对较大的学习速率。
-
对于非凸目标函数,容易陷入那些次优的局部极值点中,如在神经网路中。那么如何避免呢。
简单的问题,一般使用随机梯度下降即可解决。在深度学习里,对梯度下降进行了很多改进,比如:自适应梯度下降。在深度学习章节,我们会具体介绍。
-
轮次和批次
轮次:epoch,轮次顾名思义是把我们已有的训练集数据学习多少轮,迭代多少次。
批次:batch,批次这里指的的我们已有的训练集数据比较多的时候,一轮要学习太多数据, 那就把一轮次要学习的数据分成多个批次,一批一批数据的学习。
就好比,你要背诵一片《赤壁赋》,很长。你在背诵的时候,一段段的背诵,就是批次batch。花费了一天终于背诵下来了,以后的9天,每天都进行一轮背诵复习,这就是轮次epoch。这样,《赤壁赋》的背诵效果,就非常牢固了。
在进行,机器学习训练时,我们也要合理选择轮次和批次~
3、代码实战梯度下降
3.1、批量梯度下降BGD
这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。一元一次线性回归问题。
import numpy as np
# 1、创建数据集X,y
X = np.random.rand(100, 1)
w,b = np.random.randint(1,10,size = 2)
y = w * X + b + np.random.randn(100, 1)
# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X,np.ones((100, 1))]
# 3、创建超参数轮次
epoches = 10000
# 4、定义一个函数来调整学习率,逆时衰减
t0, t1 = 5, 1000
def learning_rate_schedule(t):
return t0/(t+t1)
# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(2, 1)
# 6、判断是否收敛,一般不会去设定阈值,而是直接采用设置相对大的迭代次数保证可以收敛
for i in range(epoches):
# 根据公式计算梯度
g = X.T.dot(X.dot(θ) - y)
# 应用梯度下降的公式去调整 θ 值
learning_rate = learning_rate_schedule(i)
θ = θ - learning_rate * g
print('真实斜率和截距是:',w,b)
print('梯度下降计算斜率和截距是:',θ)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。多元一次线性回归问题。
import numpy as np
# 1、创建数据集X,y
X = np.random.rand(100, 3)
w = np.random.randint(1,10,size = (3,1))
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)
# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X,np.ones((100, 1))]
# 3、创建超参数轮次
epoches = 10000
# 4、定义一个函数来调整学习率
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t+t1)
# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(4, 1)
# 6、判断是否收敛,一般不会去设定阈值,而是直接采用设置相对大的迭代次数保证可以收敛
for i in range(epoches):
# 根据公式计算梯度
g = X.T.dot(X.dot(θ) - y)
# 应用梯度下降的公式去调整 θ 值
learning_rate = learning_rate_schedule(i)
θ = θ - learning_rate * g
print('真实斜率和截距是:',w,b)
print('梯度下降计算斜率和截距是:',θ)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
3.2、随机梯度下降SGD
这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。一元一次线性回归问题。
import numpy as np
# 1、创建数据集X,y
X = 2*np.random.rand(100, 1)
w,b = np.random.randint(1,10,size = 2)
y = w * X + b + np.random.randn(100, 1)
# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X, np.ones((100, 1))]
# 3、创建超参数轮次、样本数量
epochs = 10000
# 4、定义一个函数来调整学习率
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t+t1)
# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(2, 1)
# 6、多次for循环实现梯度下降,最终结果收敛
for epoch in range(epochs):
# 在双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
index = np.random.randint(0,100,size = 1)[0]
X_i = X[[index]] # 打乱顺序
y_i = y[[index]]
g = X_i.T.dot(X_i.dot(θ)-y_i)
learning_rate = learning_rate_schedule(epoch)
θ = θ - learning_rate * g
print('真实斜率和截距是:',w,b)
print('梯度下降计算斜率和截距是:',θ)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。多元一次线性回归问题。
import numpy as np
# 1、创建数据集X,y
X = 2*np.random.rand(100, 5)
w = np.random.randint(1,10,size = (5,1))
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)
# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X, np.ones((100, 1))]
# 3、创建超参数轮次、样本数量
epochs = 20000
n = 100
# 4、定义一个函数来调整学习率
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t+t1)
# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(6, 1)
# 6、多次for循环实现梯度下降,最终结果收敛
for epoch in range(epochs):
# 在双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
index = np.random.randint(0,100,size = 1)[0] # 0 ~99
X_i = X[[index]] # 打乱顺序
y_i = y[[index]]
g = X_i.T.dot(X_i.dot(θ)-y_i)
learning_rate = learning_rate_schedule(epoch)
θ = θ - learning_rate * g
print('真实斜率和截距是:',w,b)
print('梯度下降计算斜率和截距是:',θ)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
3.3、小批量梯度下降MBGD
这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。一元一次线性回归问题。
import numpy as np
# 1、创建数据集X,y
X = np.random.rand(100, 1)
w,b = np.random.randint(1,10,size = 2)
y = w * X + b + np.random.randn(100, 1)
# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X, np.ones((100, 1))]
# 3、定义一个函数来调整学习率
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t+t1)
# 4、创建超参数轮次、样本数量、小批量数量
epochs = 5000
batch_size = 16
# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(2, 1)
# 6、多次for循环实现梯度下降,最终结果收敛
for epoch in range(epochs):
# 在双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
index = np.random.randint(0,100,size = batch_size)
X_batch = X[index]
y_batch = y[index]
g = X_batch.T.dot(X_batch.dot(θ)-y_batch)
learning_rate = learning_rate_schedule(epoch)
θ = θ - learning_rate * g
print('真实斜率和截距是:',w,b)
print('梯度下降计算斜率和截距是:\n',θ)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
这里我们使用了偏置项,即解决 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1。多元一次线性回归问题。
import numpy as np
# 1、创建数据集X,y
X = np.random.rand(100, 3)
w = np.random.randint(1,10,size = (3,1))
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)
# 2、使用偏置项 X_0 = 1,更新X
X = np.c_[X, np.ones((100, 1))]
# 3、定义一个函数来调整学习率
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t+t1)
# 4、创建超参数轮次、样本数量、小批量数量
epochs = 1000
batch_size = 16
# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(4, 1)
# 6、多次for循环实现梯度下降,最终结果收敛
for epoch in range(epochs):
# 在双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
index = np.random.randint(0,100,size = batch_size)
X_batch = X[index]
y_batch = y[index]
# 一次取一批数据16个样本
g = X_batch.T.dot(X_batch.dot(θ)-y_batch)
learning_rate = learning_rate_schedule(epoch)
θ = θ - learning_rate * g
print('真实斜率和截距是:\n',w,b)
print('梯度下降计算斜率和截距是:\n',θ)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35

评论记录:
回复评论: