[算法]——分治&归并（一）

 

目录

一、前言

二、正文

1.排序数组

1.1 题目解析

1.2 算法原理

1.3 具体代码

2.交易逆序对的总数

2.1 题目解析

2.2 算法原理

2.3 具体代码

三、结语

一、前言

        本文将为大家带来算法新一趴——分治&归并的学习，希望大家能够从中有所收获，如有不足，欢迎小伙伴们在评论区指出呀！！！

二、正文

1.排序数组

1. 排序数组 - 【力扣】

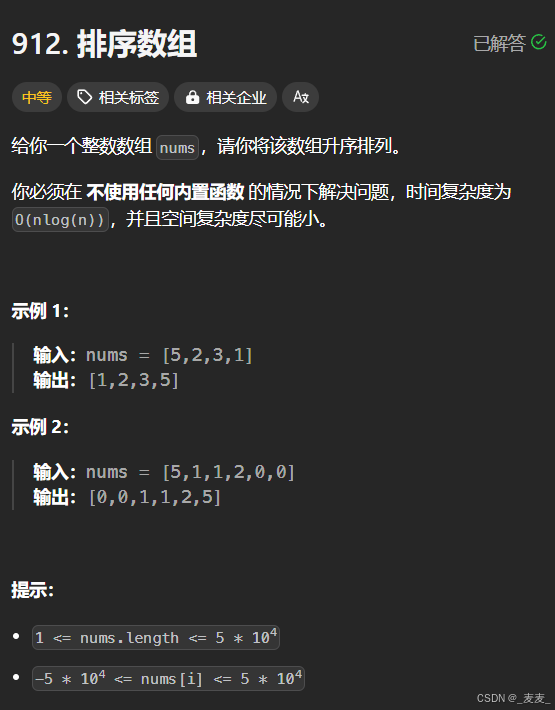
1.1 题目解析

        对于本题来说，题目的要求很简单，就是要求我们能够将所给的数组以升序进行排序。该题目也是很经典的排序题，本文只采取其中一种归并排序进行讲解，至于其他的排序，可转移至博主下面几篇文章，当然其中也包括更为细致的归并排序的讲解。

归并排序和计数排序

插入排序与希尔排序

1.2 算法原理

        本题要求我们将无序的数组处理成升序的数组。那么我们想，如果想要整个数组有序，是不是可以先以数组的中间为界，让左边有序，右边也有序，再将左右两边合并起来就可以了。那么如何实现左右两边都有序，是不是也要以左右两边各自中间为界，左边部分的左右两边有序，右边部分的左右两边有序，再将各自左右两边合并……直至分到只有一个元素，就不用排序了，那么上述过程，我们将一个很大的问题，即对整个数组进行排序的过程，分为排序左右两个部分，左右两部分再各自对内部左右两部分排序，然后在合并这样子一个将大问题切分成小问题的过程，就属于分治的过程，而采用这种分治思想的排序我们也叫做归并排序。

        具体的实现过程:

        1.选取中间点mid来换分数组的左右区间

        2.把左右区间进行排序

        3.合并两个有序数组，将其放到辅助数组tmp中（避免合并过程对原数组元素进行覆盖）

        4.处理原数组，即将辅助数组的元素拷贝到原数组

1.3 具体代码

  1. class Solution {
  2. public:
  3.     vector<int> sortArray(vector<int>& nums) {
  4.         //归并排序
  5.         vector<int> tmps=nums;
  6.         Mmerge_sort(nums,0,nums.size()-1,tmps);
  7.         return nums;
  8.     }
  9.  
  10.     void Merge_sort(vector<int>& nums,int left,int right,vector<int>& tmps)
  11.     {
  12.         if(left==right) return;
  13.         //1. 选择中间点划分区间
  14.         int mid=left+(right-left)/2;
  15.         
  16.         //2. 把左右区间排序
  17.         Imerge_sort(nums,left,mid,tmps);
  18.         Imerge_sort(nums,mid+1,right,tmps);
  19.         
  20.         //3. 合并两个有序数组
  21.         int cur1=left,cur2=mid+1,i=left;
  22.         while(cur1 <= mid && cur2<=right)
  23.             tmps[i++]=nums[cur1]<=nums[cur2]?nums[cur1++]:nums[cur2++];
  24.         while(cur1<=mid) tmps[i++]=nums[cur1++];
  25.         while(cur2<=right) tmps[i++]=nums[cur2++]; 
  26.         // 处理原数组
  27.         for(int j=left;j<=right;j++)
  28.         {
  29.             nums[j]=tmps[j];
  30.         }
  31.     }
  32. };

2.交易逆序对的总数

2.交易逆序对的总数 - 【力扣】

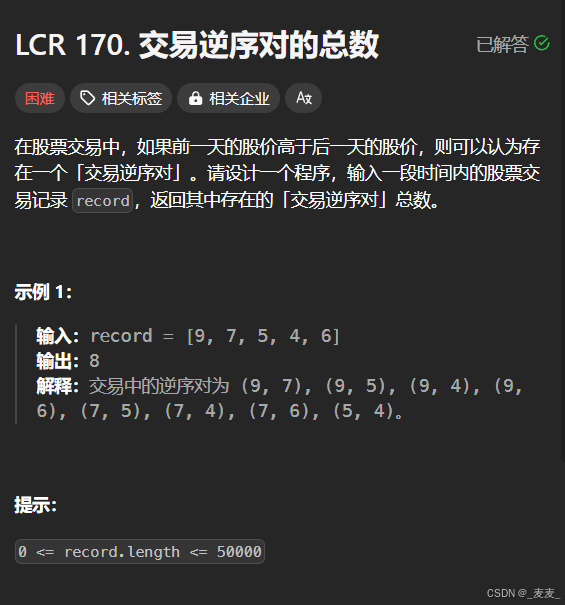
2.1 题目解析

        本题要求我们找出所给数组中所有的逆序对，并统计其数量来返回。那么什么是逆序对，也就是在该数组中我们任意选取两个元素，只要前者的元素比后者的元素大（顺序一定是前者大于后者），即说明两者组成了一个逆序对。

        我们以【9,7,5,4,6】为例，我们很容易发现（9,7）中，前者9大于后者的7，因此（9,7）就属于一个逆序对，同理我们还可以找到其他的逆序对(9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)，总共加起来就是有8个逆序对。

2.2 算法原理

        这题其实与上一题的思路大体相同，当我们想要找到整个数组的逆序对，是不是可以先将这个数组分为两部分，先找到左右两部分各自的逆序对，再找左右两部分的逆序对。而找左右两部分各自的逆序对，是不是依旧是左边部分划分为左右两部分，再加上左右的，右边部分划分为左右两部分，再加上左右的……直至分到一个元素不能再继续划分为止

        因此本题也可以采用分治的思想，按照上面的思路已经可以做出这道题目了，但是我们还可以再优化一步，就是当我们在判断两个元素是否为逆序对的时候，其实就相当于在做归并排序的统计一左一右这步的判断过程，因此我们可以再统计左右两部分的逆序对时，就可以顺便将左右两部分归并排序，方便下一次的逆序对的统计，从而提高了效率。具体的代码思路可以参考上一题的归并排序

        细心的小伙伴会发现上一题我们的归并排序是采取降序的版本，但其实归并排序也可以有升序的版本，因此对于本题来说，其实是有两种方法的，一种升序，一种降序。

2.3 具体代码

  1. class Solution {
  2. public:
  3.     int tmp[50001];
  4.     int reversePairs(vector<int>& record) {
  5.         return Mmerge_count(record,0,record.size()-1);
  6.     }
  7.  
  8.     //降序版
  9.     int Mmerge_count(vector<int>& nums,int left ,int right)
  10.     {
  11.         
  12.         if(left>= right) return 0;
  13.         int mid=left+(right-left)/2;
  14.         int ret =0;
  15.         //分别单独统计左右两个部分
  16.         ret=Mmerge_count(nums,left,mid)+Mmerge_count(nums,mid+1,right);
  17.         //统计一左一右
  18.         int cur1=left,cur2=mid+1,i=0;
  19.         while(cur1 <= mid &&cur2 <=right)
  20.         {
  21.             if(nums[cur1] <= nums[cur2] )
  22.             {
  23.                  tmp[i++]=nums[cur2++];
  24.             }
  25.             else {
  26.                 ret+=right-cur2+1;
  27.                 tmp[i++]=nums[cur1++];
  28.             }
  29.         }
  30.         while(cur1<=mid) tmp[i++]=nums[cur1++];
  31.         while(cur2<=right) tmp[i++]=nums[cur2++];
  32.         for(int j=left;j<=right;j++)
  33.             nums[j]=tmp[j-left];
  34.         return ret;
  35.     }
  36.  
  37.  
  38.     //升序版
  39.     int Mmerge_count(vector<int>& nums,int left ,int right)
  40.     {
  41.         
  42.         if(left>= right) return 0;
  43.         int mid=left+(right-left)/2;
  44.         int ret =0;
  45.         //分别单独统计左右两个部分
  46.         ret=Mmerge_count(nums,left,mid)+Mmerge_count(nums,mid+1,right);
  47.         //统计一左一右
  48.         int cur1=left,cur2=mid+1,i=0;
  49.         while(cur1 <= mid &&cur2 <=right)
  50.         {
  51.             if(nums[cur1] <= nums[cur2] )
  52.             {
  53.                  tmp[i++]=nums[cur1++];
  54.             }
  55.             else {
  56.                 ret+=mid-cur1+1;
  57.                 tmp[i++]=nums[cur2++];
  58.             }
  59.         }
  60.         while(cur1<=mid) tmp[i++]=nums[cur1++];
  61.         while(cur2<=right) tmp[i++]=nums[cur2++];
  62.         for(int j=left;j<=right;j++)
  63.             nums[j]=tmp[j-left];
  64.         return ret;
  65.     }
  66. };

三、结语

       

        到此为止，本文有关分治中归并的部分内容到此结束了，如有不足之处，欢迎小伙伴们指出呀！

         关注我 _麦麦_分享更多干货：_麦麦_-CSDN博客

         大家的「关注❤️ + 点赞? + 收藏⭐」就是我创作的最大动力！谢谢大家的支持，我们下期见！

        欢迎大家参观我的算法专栏：

麦麦的算法专栏https://blog.csdn.net/m0_73953114/category_12866812.html

一枚积极学习，乐于分享的苏苏子
QQ名片
注：本文转载自blog.csdn.net的_麦麦_的文章"https://blog.csdn.net/m0_73953114/article/details/145446279"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！