LeetCode 第111题：二叉树的最小深度

LeetCode 第111题：二叉树的最小深度

题目描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明： 叶子节点是指没有子节点的节点。

难度

简单

题目链接

点击在LeetCode中查看题目

示例

示例 1：

示例1

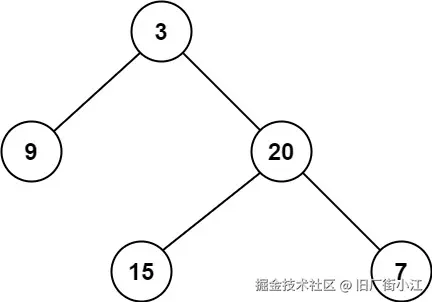
csharp
 代码解读
复制代码
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

csharp
 代码解读
复制代码
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示

  • 树中节点数的范围在 [0, 10^5] 内
  • -1000 <= Node.val <= 1000

解题思路

方法一：深度优先搜索（DFS）

最直观的方法是使用递归进行深度优先搜索。对于每个节点，我们需要：

关键点：

  • 如果节点为空，返回0
  • 如果节点是叶子节点（左右子节点都为空），返回1
  • 如果节点的左子树为空，返回右子树的最小深度+1
  • 如果节点的右子树为空，返回左子树的最小深度+1
  • 如果节点的左右子树都不为空，返回左右子树最小深度的较小值+1

具体步骤：

  1. 如果根节点为空，返回0
  2. 如果根节点的左右子节点都为空，返回1
  3. 如果根节点的左子节点为空，返回右子树的最小深度+1
  4. 如果根节点的右子节点为空，返回左子树的最小深度+1
  5. 如果根节点的左右子节点都不为空，返回左右子树最小深度的较小值+1

时间复杂度：O(n)，其中n是树中节点的数量，最坏情况下需要遍历所有节点 空间复杂度：O(h)，其中h是树的高度，递归调用栈的深度

方法二：广度优先搜索（BFS）

使用广度优先搜索可以更高效地找到最小深度，因为BFS会按层遍历，一旦找到第一个叶子节点，就可以立即返回当前深度。

关键点：

  • 使用队列进行层序遍历
  • 记录当前遍历的层数
  • 一旦找到叶子节点，立即返回当前层数

具体步骤：

  1. 如果根节点为空，返回0
  2. 初始化队列，将根节点入队，深度设为1
  3. 当队列不为空时，执行以下操作： a. 获取当前层的节点数量 b. 遍历当前层的所有节点 c. 对于每个节点，检查是否为叶子节点，如果是，返回当前深度 d. 如果不是叶子节点，将其非空子节点加入队列
  4. 深度加1，继续下一层的遍历

时间复杂度：O(n)，最坏情况下需要遍历所有节点 空间复杂度：O(n)，队列中最多存储n个节点

图解思路

方法一：DFS递归过程分析表

节点左子树右子树最小深度说明
39202左子树深度为1，右子树深度为2，取较小值1+1=2
9nullnull1叶子节点，深度为1
201572左右子树深度均为1，取较小值1+1=2
15nullnull1叶子节点，深度为1
7nullnull1叶子节点，深度为1

方法二：BFS层序遍历过程表

层数队列内容是否找到叶子节点说明
1[3]否根节点不是叶子节点
2[9, 20]是节点9是叶子节点，返回当前层数2

代码实现

C# 实现

csharp
 代码解读
复制代码
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    // 方法一：深度优先搜索（DFS）
    public int MinDepth(TreeNode root) {
        // 如果根节点为空，返回0
        if (root == null) {
            return 0;
        }
    
        // 如果是叶子节点，返回1
        if (root.left == null && root.right == null) {
            return 1;
        }
    
        // 如果左子树为空，返回右子树的最小深度+1
        if (root.left == null) {
            return MinDepth(root.right) + 1;
        }
    
        // 如果右子树为空，返回左子树的最小深度+1
        if (root.right == null) {
            return MinDepth(root.left) + 1;
        }
    
        // 如果左右子树都不为空，返回左右子树最小深度的较小值+1
        return Math.Min(MinDepth(root.left), MinDepth(root.right)) + 1;
    }
  
    // 方法二：广度优先搜索（BFS）
    public int MinDepthBFS(TreeNode root) {
        // 如果根节点为空，返回0
        if (root == null) {
            return 0;
        }
    
        // 初始化队列和深度
        Queue queue = new Queue();
        queue.Enqueue(root);
        int depth = 1;
    
        // BFS层序遍历
        while (queue.Count > 0) {
            int levelSize = queue.Count;
        
            // 遍历当前层的所有节点
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.Dequeue();
            
                // 如果找到叶子节点，返回当前深度
                if (node.left == null && node.right == null) {
                    return depth;
                }
            
                // 将非空子节点加入队列
                if (node.left != null) {
                    queue.Enqueue(node.left);
                }
                if (node.right != null) {
                    queue.Enqueue(node.right);
                }
            }
        
            // 深度加1
            depth++;
        }
    
        return depth;
    }
}

Python 实现

python
 代码解读
复制代码
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # 方法一：深度优先搜索（DFS）
    def minDepth(self, root: Optional[TreeNode]) -> int:
        # 如果根节点为空，返回0
        if not root:
            return 0
    
        # 如果是叶子节点，返回1
        if not root.left and not root.right:
            return 1
    
        # 如果左子树为空，返回右子树的最小深度+1
        if not root.left:
            return self.minDepth(root.right) + 1
    
        # 如果右子树为空，返回左子树的最小深度+1
        if not root.right:
            return self.minDepth(root.left) + 1
    
        # 如果左右子树都不为空，返回左右子树最小深度的较小值+1
        return min(self.minDepth(root.left), self.minDepth(root.right)) + 1
  
    # 方法二：广度优先搜索（BFS）
    def minDepthBFS(self, root: Optional[TreeNode]) -> int:
        # 如果根节点为空，返回0
        if not root:
            return 0
    
        # 初始化队列和深度
        queue = collections.deque([(root, 1)])
    
        # BFS层序遍历
        while queue:
            node, depth = queue.popleft()
        
            # 如果找到叶子节点，返回当前深度
            if not node.left and not node.right:
                return depth
        
            # 将非空子节点加入队列
            if node.left:
                queue.append((node.left, depth + 1))
            if node.right:
                queue.append((node.right, depth + 1))
    
        return 0

C++ 实现

cpp
 代码解读
复制代码
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 方法一：深度优先搜索（DFS）
    int minDepth(TreeNode* root) {
        // 如果根节点为空，返回0
        if (root == nullptr) {
            return 0;
        }
    
        // 如果是叶子节点，返回1
        if (root->left == nullptr && root->right == nullptr) {
            return 1;
        }
    
        // 如果左子树为空，返回右子树的最小深度+1
        if (root->left == nullptr) {
            return minDepth(root->right) + 1;
        }
    
        // 如果右子树为空，返回左子树的最小深度+1
        if (root->right == nullptr) {
            return minDepth(root->left) + 1;
        }
    
        // 如果左右子树都不为空，返回左右子树最小深度的较小值+1
        return min(minDepth(root->left), minDepth(root->right)) + 1;
    }
  
    // 方法二：广度优先搜索（BFS）
    int minDepthBFS(TreeNode* root) {
        // 如果根节点为空，返回0
        if (root == nullptr) {
            return 0;
        }
    
        // 初始化队列和深度
        queueint>> q;
        q.push({root, 1});
    
        // BFS层序遍历
        while (!q.empty()) {
            TreeNode* node = q.front().first;
            int depth = q.front().second;
            q.pop();
        
            // 如果找到叶子节点，返回当前深度
            if (node->left == nullptr && node->right == nullptr) {
                return depth;
            }
        
            // 将非空子节点加入队列
            if (node->left != nullptr) {
                q.push({node->left, depth + 1});
            }
            if (node->right != nullptr) {
                q.push({node->right, depth + 1});
            }
        }
    
        return 0;
    }
};

执行结果

C# 实现

  • 执行用时：92 ms
  • 内存消耗：41.2 MB

Python 实现

  • 执行用时：48 ms
  • 内存消耗：17.5 MB

C++ 实现

  • 执行用时：232 ms
  • 内存消耗：144.2 MB

性能对比

语言执行用时内存消耗特点
C#92 ms41.2 MB递归实现简洁，性能适中
Python48 ms17.5 MB代码最简洁，在此题中性能最佳
C++232 ms144.2 MB内存占用较大，但在大规模数据上可能更高效

代码亮点

  1. 🎯 针对不同子树情况的特殊处理，避免了不必要的递归
  2. 💡 BFS方法一旦找到叶子节点立即返回，避免了不必要的遍历
  3. 🔍 正确处理了叶子节点的定义（没有子节点的节点）
  4. 🎨 代码结构清晰，逻辑分支处理完整

常见错误分析

  1. 🚫 忽略了叶子节点的定义，错误地认为任何节点都可以计算深度
  2. 🚫 没有正确处理单侧子树为空的情况，导致计算错误
  3. 🚫 在DFS中没有考虑到最小深度是到叶子节点的路径，而不是任意节点
  4. 🚫 在BFS实现中忘记检查节点是否为叶子节点，导致提前返回错误结果

解法对比

解法时间复杂度空间复杂度优点缺点
DFSO(n)O(h)实现简单，递归逻辑清晰最坏情况下可能遍历整棵树
BFSO(n)O(n)一旦找到叶子节点立即返回，通常更高效需要额外的队列空间

相关题目

注：本文转载自juejin.cn的旧厂街小江的文章"https://juejin.cn/post/7490458997541257231"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！