分治算法之循环赛问题

此最初发表于CSDN，因CSDN平台太过杂乱，在掘金平台重新发布。

  • 完善画图表达
  • 增加算法正确性的数学证明
  • 增加Python、C++、Java的源代码Gitee或GitHub仓库

题目描述

设有nn个运动员要进行网球循环赛。设计一个满足下列条件的比赛日程表：

  • 每个运动员必须与其他n−1n-1个运动员各赛一次；
  • 每个运动员一天只能赛一次；

任意运动员的地位都是对等的，所以此问题是存在问题，只需找出存在的解即可。

思考：如果增加限制条件呢？所有满足条件的比赛日程表有多少个？

解决方案要求

  1. 使用分治策略，编写程序完成。
  2. 设置数据集、测试程序，写出测试报告。
  3. 验证算法的正确性。
  4. 写出题目的具体分析过程，算法程序进行必要的解析（伪代码+源代码）。
  5. 分析所完成程序的时间复杂度。

解决方案

题目分析

特殊情况，运动员数nn为2的幂次

运动员数为2k2^k，直接二分。

比赛方案可以使用二维矩阵表达：

  1. 二维矩阵f[i][j]∈[1,n]∪{−}f[i][j]\in[1,n] \cup\{-\}，i,j∈[1,n]i,j\in[1, n]
  2. f[i][1]=if[i][1]=i，第一列表示运动员序号
  3. 列数j,j>1j, j>1表示第j−1j-1天的比赛安排
  4. 假设s=f[i][j]s=f[i][j]，则运动员ii和运动员ss在第j−1j-1天对战；特别地,f[i][j]=−f[i][j]=-表示运动员ii在第j−1j-1天休息

例如对于n=4n=4，下图左上角表示：

  • 第11天，运动员11和运动员22对战，运动员33和运动员44对战；
  • 第22天，运动员11和运动员33对战，运动员22和运动员44对战；
  • 第33天，运动员11和运动员44对战，运动员22和运动员33对战；

2^k^

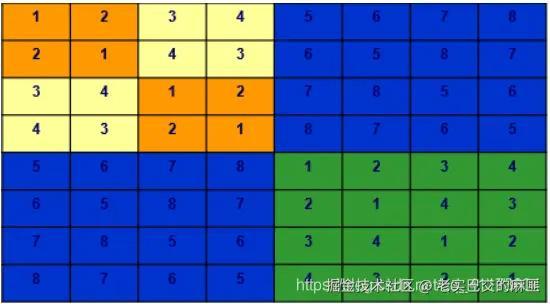
完全使用分治策略，问题规模最小是n=2n=2，可以直接构建比赛集，然后合并。将本模块，挪动到对角线位置，构成新的一个整体模块。

运动员数为2的幂次求解方案符合最基本的二分策略，不在此赘余。下面我将这种特殊情况，扩展到更一般情况，nn可以是任意整数。

一般情况，运动员数nn是任意整数
f(n)={n−1,n为偶数n,n为奇数f(n)=\left\{ \begin{array}{lr} n-1 &, n为偶数 \\ n &, n为奇数 \end{array} \right.

nn位奇数时，比赛天数为nn，每个运动员都有11天的休息时间。 nn位偶数时，比赛天数为n−1n-1天，所有运动员每天都有比赛。

分治算法的特点是：

  • 问题可以分解
  • 子问题是独立的
  • 子问题的解可以合并

分支算法一般使用递归解决，递归算法一定有终止条件，我们可以从递归函数的终止条件开始思考。

从递归终止条件看，使用脑算，计算运动员的比赛规则表：

n=2n=2，比赛需要11天，比赛日程表如下：

playerthplayer_{th}1
12
21

n=3n=3，比赛需要3天，比赛日程表如下：

playerthplayer_{th}123
123-
21-3
3-12

比赛的总时间是33天，在这三天中，每个运动员都有一天的休息时间，并且他们每个人的休息时间都不在同一天。

n=4n=4，比赛需要 33天，比赛日程表如下：

playerthplayer_{th}123
1234
2143
3412
4321

比赛总天数是33天，4=2+24=2+2，分成单独的两个队伍，队伍内先比赛，然后每个队员与另一个队伍中的每个运动员比赛。

对比n=4n=4和n=3n=3，把n=4n=4这一行删除，并且把表格中的44删除，就得到n=3n=3的表格

n=5n=5，比赛的总天数是55天，此时已经发现，没有前几个nn比较小的时候容易写了，需要使用有效的策略。

n=5n=5规模对于我来说太大了，先跳过吧。

n=6n=6，分成两组3+33+3，每一组比赛的时间是33天，合并两组需要33天，总共66天。合并方式：对角线填充。如何减少一天呢？

playerthplayer_{th}123
123-
21-3
3-12
456-
54-6
6-45

两组33天内的比赛，我们看到这是两组一模一样的表，11和44，22和55，33和66都有在同一天休息。让他们把空闲的时间利用起来。

playerthplayer_{th}123
1234
2153
3612
4561
5426
6345

剩下22天需要完成的比赛：

  • 11对战55 66
  • 22对战44 66
  • 33对战44 55

小规模的问题，可以直接心算，获得最后两天的比赛安排：

第44天 11vs55 22vs66 33vs44

第55天 11vs66 22vs44 33vs55

汇总比赛安排表：

playerthplayer_{th}12345
123456
215364
361245
456132
542613
634521

回过头来，再考虑n=5n=5，就简单多了，直接把第66行删除，然后把表格中的66删除就ok了。

playerthplayer_{th}12345
12345-
2153-4
3-1245
45-132
542-13

n=7n=7，在n=8n=8的基础上删减

n=8n=8

2的3次幂，太简单了，见上文第一个图。

n=9n=9依托于n=10n=10的计算

n=10n=10可以分成5+55+5，两个形状完全一样的表格，填补。然后在根据一定的算法补充后4天的表格。

以上，我们可以得到规律：对于n=2kn=2k，通过删除方式，直接得到n=2k−1n=2k-1的比赛表；而n=2kn=2k时可以分治为n+nn+n两组合并来求。

下面我们对合并算法进行探究

以n=6n=6为例

playerthplayer_{th}123
1234
2153
3612
4561
5426
6345

在接下来的22天，还需要完成的比赛

运动员11：55、66

运动员22：44、66

运动员33：44、55

第44天：运动员11选了55（从小到大），运动员22选66（5+15+1） ，从下一位开始，运动员33选44（7−37-3）。

第55天：运动员11选了66，运动员22选44（7−37-3），运动员33选55（8−38-3）。

规划完毕，填充比赛规划表格：

playerthplayer_{th}12345
123456
215364
361245
456132
542613
634521

n=10=5+5n=10=5+5，对于n=5n=5的表格，已经在上述得到，对n=6n=6进行掏空就行。

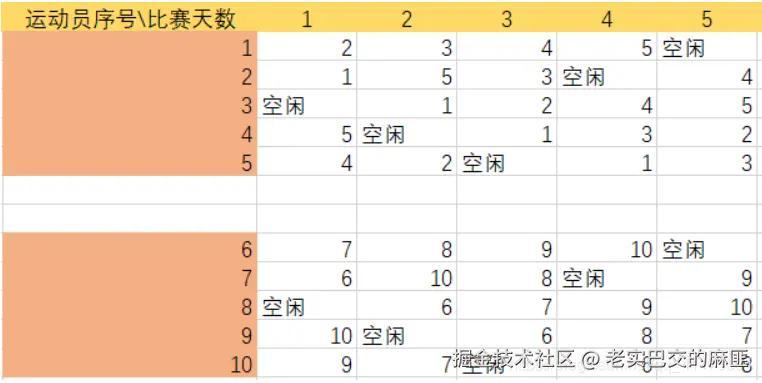
首先两组互相填补空闲时间（不能让运动员歇息一天，狠狠地push）。

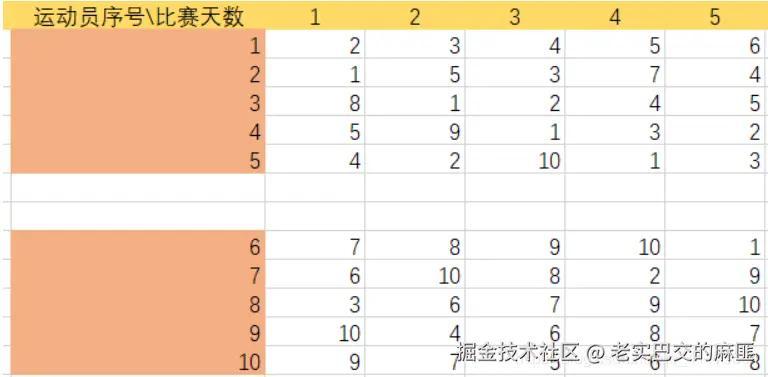得到如下表格，是前55天的比赛表： 在这里插入图片描述 在接下来的44天时间，需要比赛：

  • 运动员11：77、88、99、1010
  • 运动员22：66、88、99、1010
  • 运动员33：66、77、99、1010
  • 运动员44：66、77、88、1010
  • 运动员55：66、77、88、99

第66天：运动员1−51-5分别安排对战 7、8、9、10、67、8、9、10、6

第77天：8、9、10、6、78、9、10、6、7

第88天：9、10、6、7、89、10、6、7、8

第99天：10、6、7、8、910、6、7、8、9

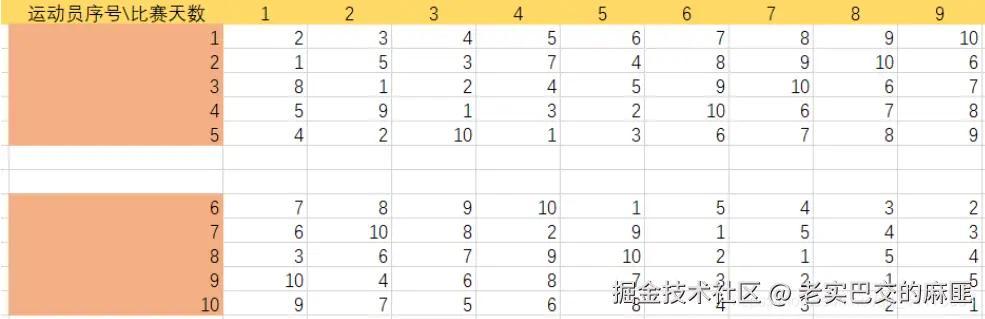总表如下： 在这里插入图片描述 因此n=10n=10的情况也得到了。

以每组首个运动员第一个需要比赛的运动员为起点，形成一个环。观察下面两图，可以看到规律。

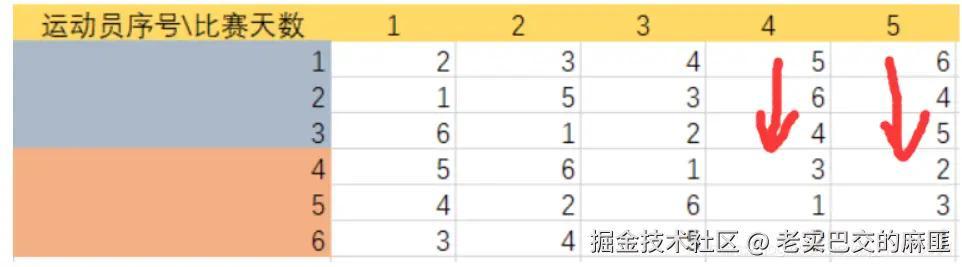
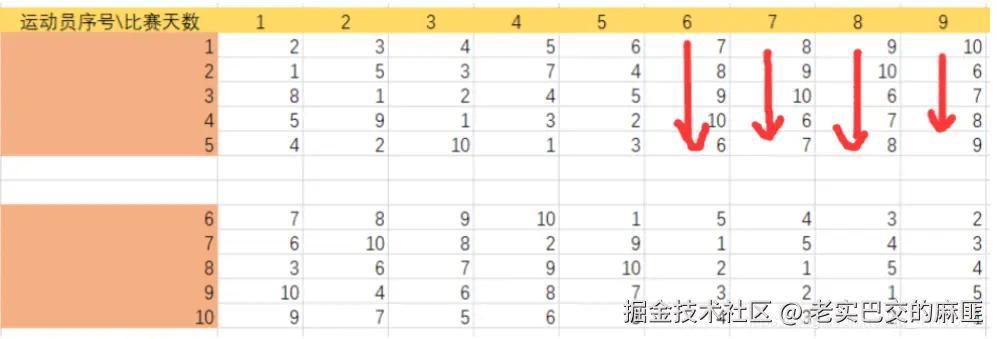
在这里插入图片描述 在这里插入图片描述

策略证明：待补充...，联系作者邮箱，共同完成，[email protected]

将以上规律进行推广

设f(m,n)f(m,n)表示对运动员序号为[m,n][m,n]比赛表的生成。

例如n=50n=50，使用分治策略，分别是f(1,25)和f(26,50)f(1, 25)和f(26, 50)，第二个表就是对第一个表中所有数字+25+25。因此问题分治成求f(1,25)f(1, 25)，然后和f(26,50)f(26, 50)合并。

以下是这个问题的递和归过程。

cpp
 代码解读
复制代码
step 1:  f(1,50) → f(1,25) U  f(26,50)                  step 18: 输出结果，结束。  

step 2:  f(1,25) → f(1,26) - f(26)                      step 17: 根据f(1,25)直接写出f(26,50)，合并为f(1,50)

step 3:  f(1,26) → f(1,13) U f(14,26)                   step 16: f(1,26)删减为f(1,25)

step 4:  f(1,13) → f(1,14) - f(14)                      step 15: 根据f(1,13)直接写出f(14,26)，合并为f(1,26)

step 5:  f(1,14) → f(1,7) U f(8,14)                     step 14: f(1,14)删减为f(1,13)

step 6: f(1,7)  → f(1,8) - f(8)                         step 13: 根据f(1,7)直接写出f(8,14)，合并为f(1,14)

step 7: f(1,8) →  f(1,4) U f(4,8)                       step 12: f(1,8)删减为f(1,7)

step 8: f(1,4) →  f(1,2) U f(3,4)                       step 11:  根据f(1,4)直接写出f(5,8)合并为f(1,8)

step 9:  直接计算 f(1,2)，根据f(1,2)直接写出f(3,4)          step 10:  合并 f(1,2) f(3,4) 得到 f(1,4)

nn可以扩展所有可计算范围：

当nn为奇数时，通过计算f(1,n+1)f(1,n+1)，然后删减n+1n+1得到

当nn为偶数时，二分，只计算前半部分，后半部分，可以直接“抄袭”前半部分😁

接下来是合并算法，根据上面的处理情况得知，前半部分和后半部分永远是等大的（因为采取二分策略的时候nn是偶数）。

当半个部分大小是偶数时，可以直接复制到对角线就OK。

当半个部分大小是奇数的，稍微困难一点，但是还是有规律可循。

首先，两个部分都在相同的位置存在空闲，因此让对应部分相互比赛，如下图

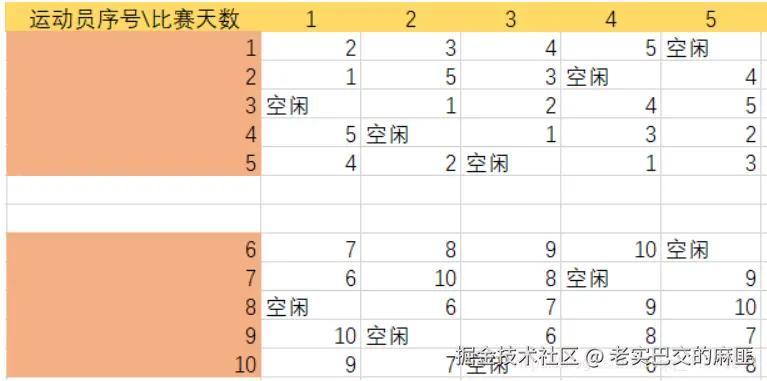
在这里插入图片描述

首先填补前5天的空闲时间后得到

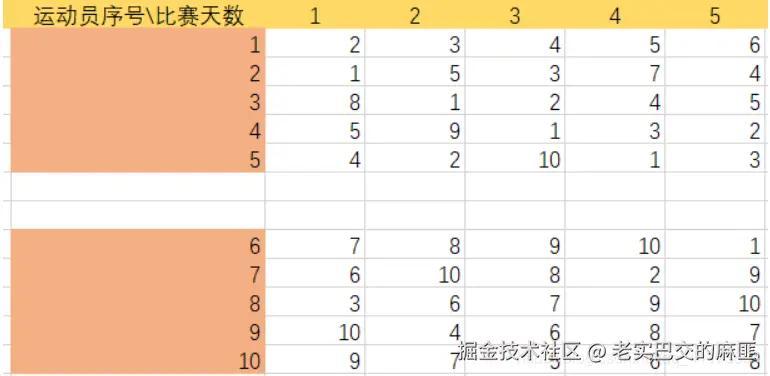
然后填充后4天的表格，我填写情况如下

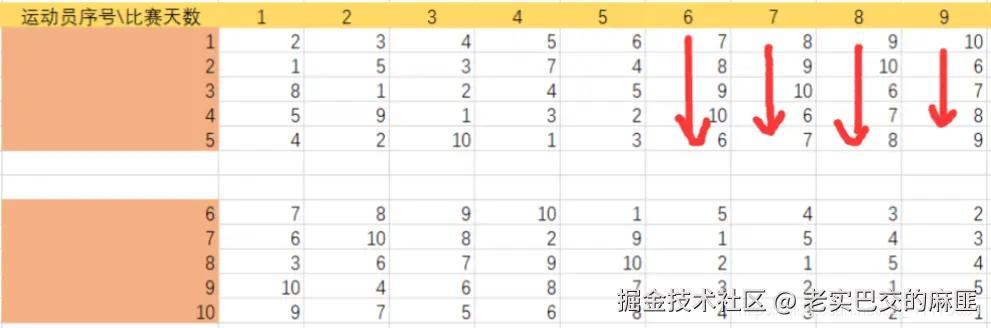
在这里插入图片描述

我们只需填写1−51-5号运动员，那么对应的6−106-10号运动员也就直接填写完毕。

看第6−96-9天，纵向看可以发现：7、8、9、10、67、8、9、10、6围成了一个环，后面的时间都是从前一个的头结点的下一个为头节点，开始循环。

所以我们只需要找到第66天的头就行了，第66天的头是7=1+67=1+6（我们看到其实第一排是有序的1−101-10），所以算法分析到此结束。

代码实现

伪代码
c
 代码解读
复制代码
void raceTable(int left,int right) //待求的左边界和右边界
{
    if(size==2)
    {
        填表格，结束
    }
    if(size为奇数)
    {
        计算 raceTable(pos,size+1);
    }
    else{
        raceTable(pos,size/2); //分治策略，计算前半部分
        copyTable(pos,right); //根据上式前半部分的计算，直接写出后半部分。
        Union(pos,size/2);//合并两部分
    }
}
void Union(int left,int mid,int right)
{
    if(mid为奇数)
    两组相对于，填补前n天的空闲时间;
    
    循环左下边放入到右上角，同时放置对应的右下角（同时进行的）
}
void copyTable(pos,right)
分模块完成代码

(1) 生成比赛表函数

c
 代码解读
复制代码
void raceTable(int left,int right)
{
    int size=right-left+1;
    if(size==2) //递归终点
    {
        arr[left][1]=right;
        arr[right][1]=left;
        return;
    }
    if(size%2==1) //当前计算规模是奇数，我们计算大一个规模
    {
        raceTable(left,right+1);
        return;
    }
    //以下是size是2的倍数
    int mid=(left+right)/2;
    raceTable(left,mid);
    copyTable(left,mid,right); //直接复制上面计算得到的
    Union(left,mid,right);
}

(2) copyTable函数，根据前半部分直接完成后半部分

c
 代码解读
复制代码
void copyTable(int left,int mid,int right) //复制函数
{
    int size=right-left+1;
    int i,j,m;
    if(size%2==1) //奇数
        m=size;
    else
        m=size-1;
    for(i=right;i>mid;i--)
        for(j=1;j<=m;j++)
            arr[i][j]=arr[i-mid][j]+mid;
}

(3) 合并函数，将前半部分和后半部分合并

c
 代码解读
复制代码
void Union(int left,int mid,int right)
{
    int i,j;
    int size=right-left+1;
    if(mid%2==1) //如果size为奇数，需要首先填补前几天的空白
    {
        for(i=left;i<=mid;i++)
            for(j=1;j<=size;j++)
            {
                if(arr[i][j]>mid) //这个位置是空的
                {
                    arr[i][j]=i+mid;
                    arr[i+mid][j]=i;
                    break;
                }
            }
    }
    //下面开始合并
    if(mid%2==0)  //每一半都是偶数，直接移到对角线
    {
        for(j=mid;j
            for(i=1;i<=mid;i++)
            {
                int t=arr[i+mid][j-mid];
                arr[i][j]=t;
                arr[t][j]=i;
            }
    }
    else{
        //结合规律，开始合并
        for(j=mid+1;j
            for(i=1;i<=mid;i++)
            {
                int t=i+j;
                if(t>right)
                    t-=mid;
                arr[i][j]=t;
                arr[t][j]=i;
            }
    }

}

//需要将arr的0位置初始化，以便来完成上述移动
    for(int i=1;i<=n;i++)
        arr[i][0]=i;
完整源代码
c
 代码解读
复制代码
#include 
#include 
using namespace std;
const int maxn=1005;
int arr[maxn][maxn]={0};
int n;

bool isCorrect()
{
    int i,j;
    int days;
    if(n%2==0)
        days=n-1;
    else
        days=n;
    bool isAppearence[n+1];
    for(i=1;i<=n;i++) //行
    {
        fill(isAppearence,isAppearence+n+1,false); //初始化数组
        for(j=1;j<=days;j++)
        {
            int t=arr[i][j];
            if(t==0)
                continue;
            if(isAppearence[t])  //在这一行中之前已经出现过了
                return false;
            isAppearence[t]=true;
            if(arr[t][j]!=i || t>n || t<1 ) //运动员t在第j天的对手必须是i,t必须是正确运动员1~n
                return false;
        }
    }
    return true;
}
void Union(int left,int mid,int right)
{
    int i,j;
    int size=right-left+1;
    if(mid%2==1) //如果size为奇数，需要首先填补前几天的空白
    {
        for(i=left;i<=mid;i++)
            for(j=1;j<=size;j++)
            {
                if(arr[i][j]>mid) //这个位置是空的
                {
                    arr[i][j]=i+mid;
                    arr[i+mid][j]=i;
                    break;
                }
            }
    }
    //下面开始合并
    if(mid%2==0)
    {
        for(j=mid;j
            for(i=1;i<=mid;i++)
            {
                int t=arr[i+mid][j-mid];
                arr[i][j]=t;
                arr[t][j]=i;
            }
    }
    else{
        //结合规律，开始合并
        //size=6 mid=3 left=1 right=6
        for(j=mid+1;j
            for(i=1;i<=mid;i++)
            {
                int t=i+j;
                if(t>right)
                    t-=mid;
                arr[i][j]=t;
                arr[t][j]=i;
            }
    }

}
void copyTable(int left,int mid,int right) //复制函数
{
    int size=right-left+1;
    int i,j,m;
    if(size%2==1) //奇数
        m=size;
    else
        m=size-1;
    for(i=right;i>mid;i--)
        for(j=1;j<=m;j++)
            arr[i][j]=arr[i-mid][j]+mid;
}
void raceTable(int left,int right)
{
    int size=right-left+1;
    if(size==2)
    {
        arr[left][1]=right;
        arr[right][1]=left;
        return;
    }
    if(size%2==1)
    {
        raceTable(left,right+1);
        return;
    }
    //以下是size是2的倍数
    int mid=(left+right)/2;
    raceTable(left,mid);
    copyTable(left,mid,right); //直接复制上面计算得到的
    Union(left,mid,right);
}
int main() {
    cin>>n;
    for(int i=1;i<=n;i++)
        arr[i][0]=i;
    raceTable(1,n);
    int t=n%2==0?n-1:n;
    for(int i=1;i<=n;i++)
    {
        printf("%d: ",i);
        for(int j=1;j<=t;j++)
        {
            if(arr[i][j]==n+1) //空闲时间
                arr[i][j]=0;
            printf(" %d",arr[i][j]);
        }
        printf("\n");
    }
    if(isCorrect())
        cout<<"true"<<endl;
    else
        cout<<"false"<<endl;
    return 0;
}

算法正确性测试

nn为奇数，比赛在nn天内完成； nn为偶数，比赛在n−1n-1天内完成。

  1. 对于每ii行，1−n1-n除了ii必须都出现，并且只出现11次；
  2. 如果某一天ii和ss比赛，那么也一定是ss和ii比赛，即若f[i][j]=sf[i][j]=s，则f[s][j]=if[s][j]=i
  3. 每个运动员每天只能比赛一次，列表示为天数，那么每列每个运动员编号不能出现两次。考虑到，如果某列一个运动员出现了不少于2次，而该运动员当天比赛的队伍的格子只能是一个队伍，这与条件2矛盾，可以认为，如果不满足条件3则一定不满足条件2，因此可以不必判断条件3。
  4. 必须保证出现在表格中的运动员编号是有效的，即[1,n][1, n]，不是这个范围内的数则输出错误信息。

以下是判断算法正确性的代码

c
 代码解读
复制代码
int n;
int arr[maxn][maxn];
bool isCorrect()
{
    int i,j;
    int days;
    if(n%2==0)
        days=n-1;
    else
        days=n;
    bool isAppearence[n+1];
    for(i=1;i<=n;i++) //行
    {
        fill(isAppearence,isAppearence+n+1,false); //初始化数组
        for(j=1;j<=days;j++)
        {
            int t=arr[i][j];
            if(t==0) //空闲时间的标志
                continue;
            if(isAppearence[t])  //在这一行中之前已经出现过了
                return false;
            isAppearence[t]=true;
            if(arr[t][j]!=i || t>n || t<1 ) //运动员t在第j天的对手必须是i,t必须是正确运动员1~n
                return false;
        }
    }
    return true;
}

测试

nn取2−10002-1000，使用上述测试算法，输出测试结果，确保全部输出为True。

c
 代码解读
复制代码
{
	int i;
	for(i=2;i<=1000;i++)
	{
		fill(arr,arr+maxn*maxn,0);
        raceTable(1,i);
        if( isCorrect() )
            printf("True\n");
        else
            printf("False\n");
	}
}

输出结果为100个True。

算法时间复杂度分析

此题目是二维矩阵，对于n，很容易知道时间复杂度下限是Ω(n2)Ω(n^2)

nn为奇数f(n)=f(n+1)f(n) = f(n+1)

nn为偶数 f(n)=f(n/2)+(n/2)×(n/2)+2×(n/2)×(n/2)f(n) = f(n/2) + (n/2)×(n/2) + 2×(n/2)×(n/2)

因此可以递推得到时间复杂度是O(n2)O(n^2)

验证算法正确性是对一个二维矩阵的枚举过程，时间复杂度O(n2)O(n^2)。

注：本文转载自juejin.cn的老实巴交的麻匪的文章"https://juejin.cn/post/7423762647780933672"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！