张正友标定法
\quad
张正友标定法是一种广泛使用的相机标定方法,它通过一组已知尺寸的标定板图像来估计相机的内外参数。
 \quad
张正友标定法论文原文
\quad
张正友标定法论文原文
四大坐标系
\quad
在计算机视觉中,理解世界坐标系、相机坐标系、图像坐标系和像素坐标系之间的转换关系非常重要,是开展计算机视觉相关工作的重要基础。通过相机的内外参数,可以实现从世界坐标到图像坐标的精确转换,这对于三维重建、定位、自动驾驶等应用至关重要。
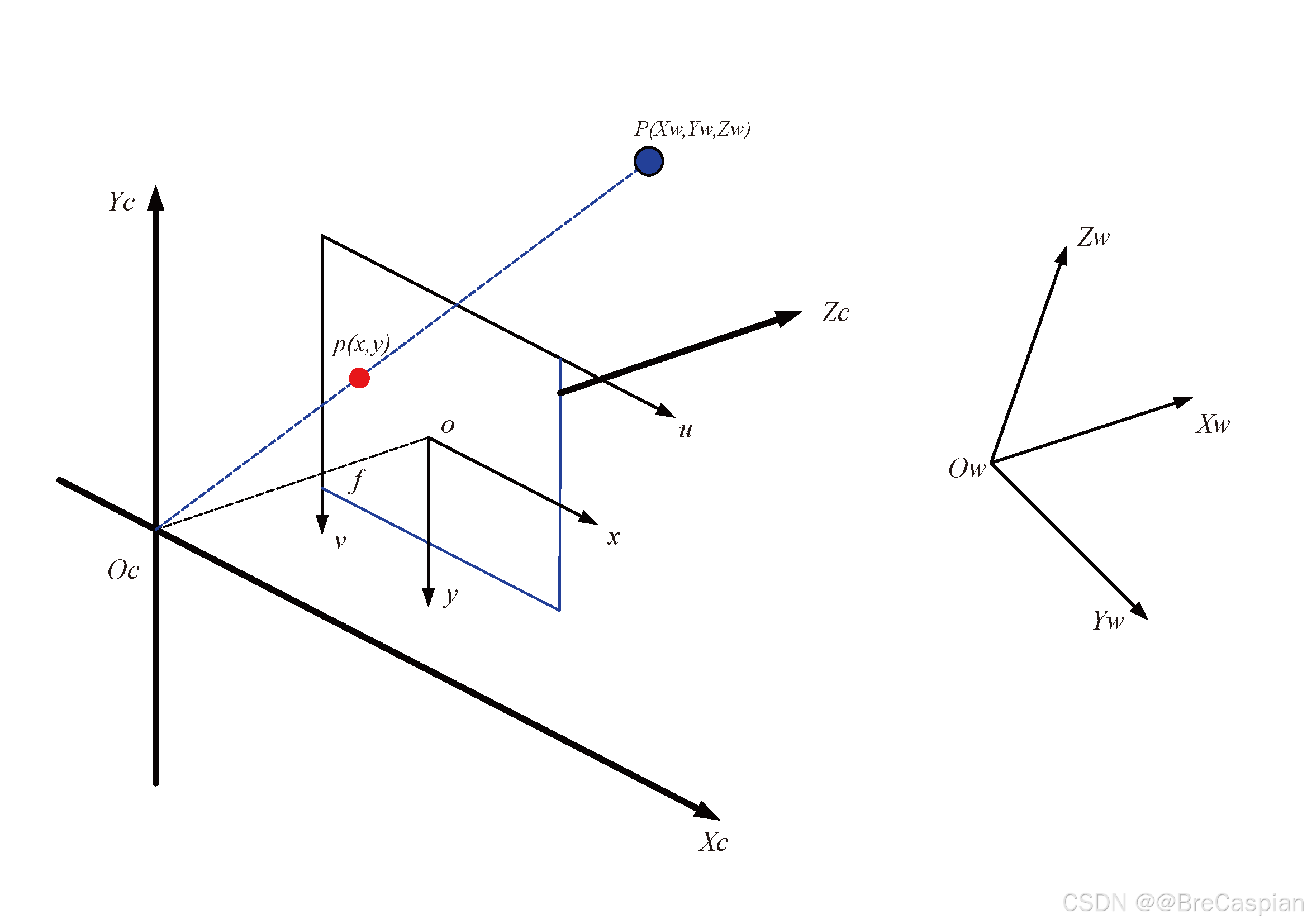
1. 坐标系定义
\quad 世界坐标系 ( O w − X w Y w Z w ) (O_w−X_wY_wZ_w) (Ow−XwYwZw): 该坐标系描述了物体在真实世界中的位置,单位通常为米 ( m ) (m) (m)
\quad 相机坐标系 ( O c − X c Y c Z c ) (O_c−X_cY_cZ_c) (Oc−XcYcZc): 该坐标系描述了相机内部的坐标系统,光心(相机位置)为原点,单位为米 ( m ) (m) (m)
\quad 图像坐标系 ( O x y ) (Oxy) (Oxy): 该坐标系位于相机的成像平面上,原点通常是图像的中心,单位为毫米 ( m m ) (mm) (mm)
\quad 像素坐标系 ( u v ) (uv) (uv): 该坐标系位于图像的左上角,单位为像素 ( p i x e l ) (pixel) (pixel),通常用来描述图像中的像素位置
2. 坐标之间的转换
\quad 在实际应用中,需要进行从一个坐标系到另一个坐标系的转换。以下是常见的坐标转换方法。
2.1 世界坐标系到相机坐标系的转换
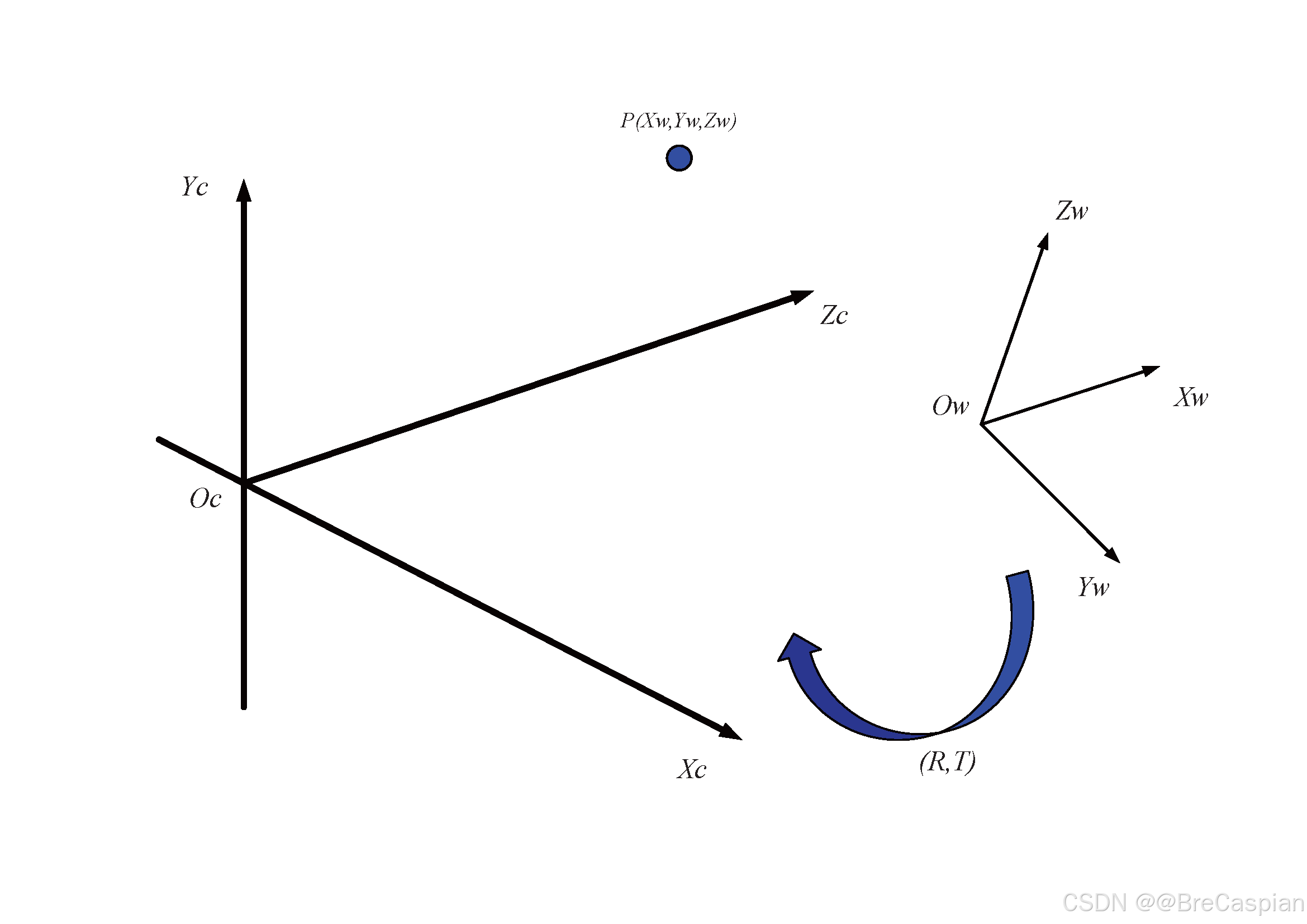
\quad 从世界坐标系变换到相机坐标系属于刚体变换(即不涉及形变,只有旋转和平移)。具体的转换关系如下:
\quad
旋转矩阵
(
R
)
(R)
(R) 描述世界坐标系到相机坐标系的旋转关系
\quad
平移向量
(
T
)
(T)
(T) 描述相机坐标系的原点与世界坐标系原点之间的平移关系
\quad 数学表示为:

\quad 齐次坐标形式表示为:

\quad 这里, ( R 3 × 3 ) ( R_{3 \times 3} ) (R3×3) 是旋转矩阵, ( T 3 × 1 ) ( T_{3 \times 1} ) (T3×1) 是平移向量。
2.2 相机坐标系到图像坐标系的转换
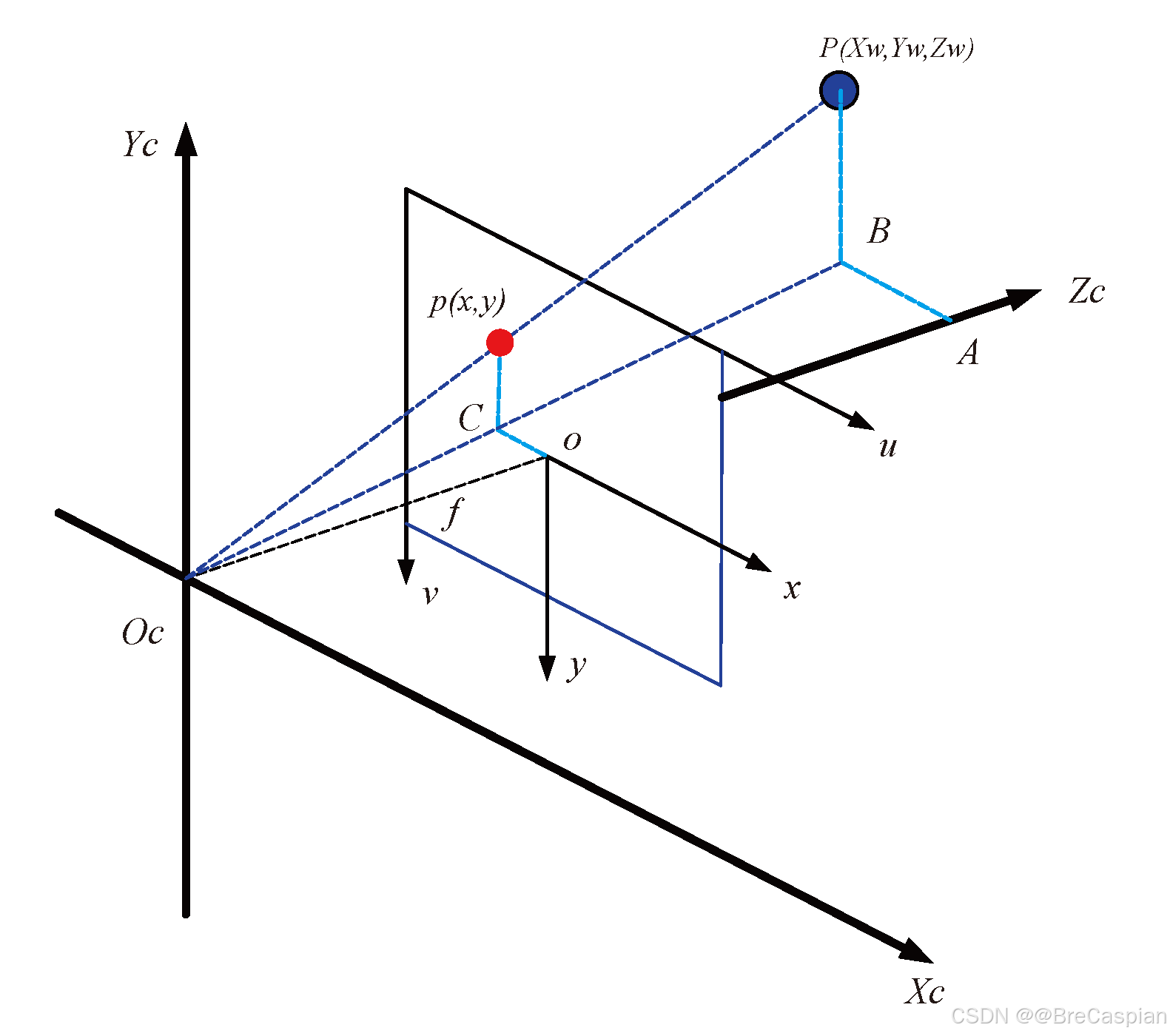
\quad 相机坐标系到图像坐标系的转换是一个透视投影过程。通过投影公式将三维空间中的点映射到二维图像平面。
\quad 投影关系可以表示为:

\quad
其中,
\quad
(
f
)
( f )
(f) 是相机的焦距,
\quad
(
(
X
c
,
Y
c
,
Z
c
)
)
( (X_c, Y_c, Z_c) )
((Xc,Yc,Zc)) 是点在相机坐标系中的坐标,
\quad
(
(
x
,
y
)
)
( (x, y) )
((x,y)) 是该点在图像坐标系中的位置。
\quad 齐次坐标形式表示为:

\quad 这个投影过程实现了三维到二维的转换,注意,深度信息 ( Z c ) ( Z_c ) (Zc) 在此过程中起到了关键作用。
2.3 图像坐标系到像素坐标系的转换
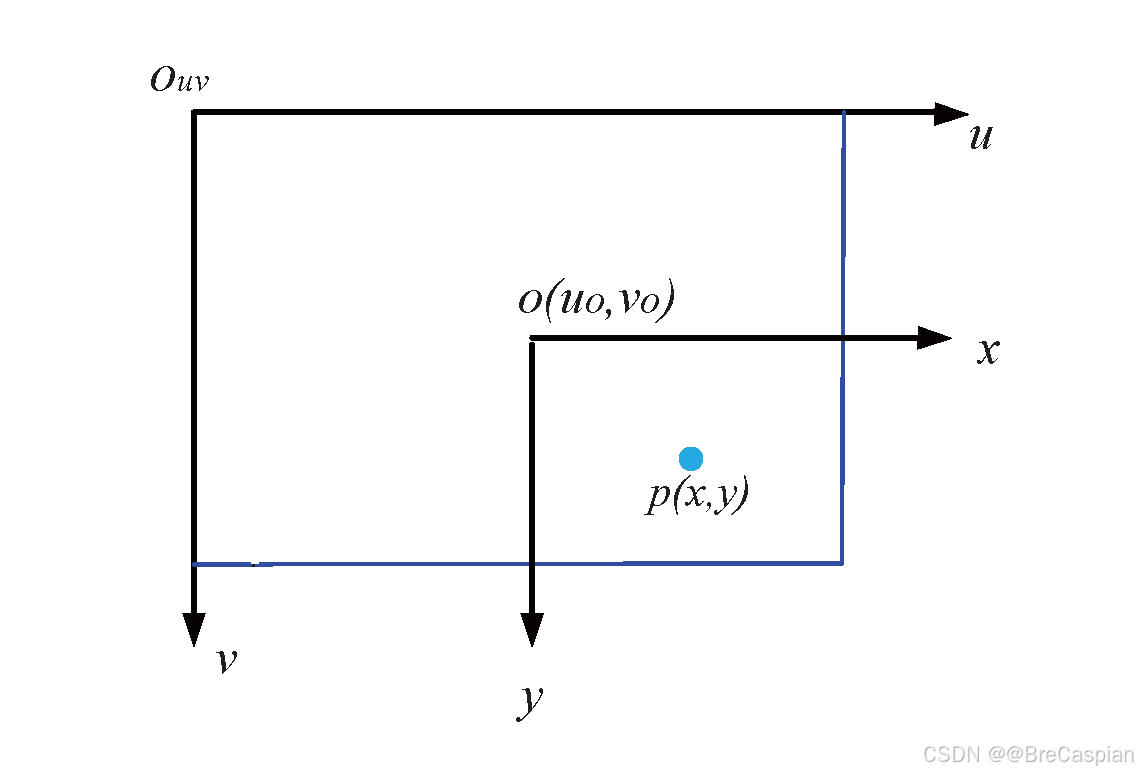
\quad 图像坐标系和像素坐标系之间的转换主要是因为它们的原点和单位不同。图像坐标系的原点位于图像的中心,单位通常为毫米,而像素坐标系的原点位于图像的左上角,单位是像素。
\quad
转换关系如下:
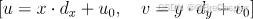
\quad
其中,
\quad
(
d
x
)
( d_x )
(dx) 和
(
d
y
)
( d_y )
(dy) 分别表示每个像素的物理大小(单位为毫米),
(
u
0
)
( u_0 )
(u0) 和
(
v
0
)
( v_0 )
(v0) 是图像坐标系原点到像素坐标系原点的偏移量。
\quad 齐次坐标形式表示为:

2.4 综合转换
\quad 综合起来,从世界坐标系到像素坐标系的完整转换公式可以写为:
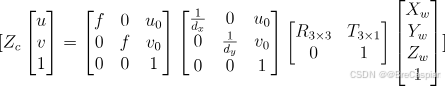
\quad 其中, ( R 3 × 3 ) ( R_{3 \times 3} ) (R3×3) 和 ( T 3 × 1 ) ( T_{3 \times 1} ) (T3×1) 是相机的外参(旋转矩阵和平移向量),而 ( f ) ( f ) (f), ( u 0 ) ( u_0 ) (u0), ( v 0 ) ( v_0 ) (v0), ( d x ) ( d_x ) (dx), ( d y ) ( d_y ) (dy) 是相机的内参。
3. 相机的内参和外参
\quad
内参
(
I
n
t
r
i
n
s
i
c
P
a
r
a
m
e
t
e
r
s
)
(Intrinsic Parameters)
(IntrinsicParameters):
\quad
\quad
相机的内参包括焦距
(
f
)
( f )
(f)
\quad
\quad
主点
(
u
0
,
v
0
)
(u_0, v_0)
(u0,v0)
\quad
\quad
每个像素的物理大小
(
d
x
,
d
y
)
(d_x, d_y)
(dx,dy)
\quad
这些参数可以通过相机标定得到。
\quad
外参
(
E
x
t
r
i
n
s
i
c
P
a
r
a
m
e
t
e
r
s
)
(Extrinsic Parameters)
(ExtrinsicParameters):
\quad
\quad
外参包括旋转矩阵
(
R
)
( R )
(R)
\quad
\quad
平移向量
(
T
)
( T )
(T)
\quad
表示相机相对于世界坐标系的位置和姿态。
\quad 这些参数也可以通过标定得到,通常使用张正友标定法来估计。
相机模型
\quad 相机的成像过程通常使用针孔相机模型来描述。针孔相机模型假设相机的光学系统是一个小孔,世界中的三维点通过该孔投影到图像平面上。相机模型主要包括内参和外参。

内参 ( I n t r i n s i c P a r a m e t e r s ) (Intrinsic Parameters) (IntrinsicParameters)
\quad 内参是描述相机自身特性的参数,主要包括焦距、主点和畸变系数等:
\quad
焦距
(
f
x
)
( f_x )
(fx) 和
(
f
y
)
( f_y )
(fy):分别沿
(
x
)
( x )
(x) 和
(
y
)
( y )
(y) 方向的焦距
\quad
主点
(
c
x
,
c
y
)
(c_x, c_y)
(cx,cy):图像坐标系的原点,通常是图像的中心
\quad
畸变系数:描述镜头畸变(如径向畸变和切向畸变)
\quad 相机的内参矩阵 ( K ) ( K ) (K)表示为:
K
=
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
K =
外参 ( E x t r i n s i c P a r a m e t e r s ) (Extrinsic Parameters) (ExtrinsicParameters)
\quad 外参描述相机与世界坐标系之间的相对位置和方向。它包括旋转矩阵 ( R ) (R) (R) 和平移向量 ( T ) ( T ) (T),它们将世界坐标系中的三维点转换到相机坐标系。

\quad 其中, ( X , Y , Z ) (X, Y, Z) (X,Y,Z) 是世界坐标系中的点, ( x , y ) (x, y) (x,y) 是图像平面上的点。
投影模型
\quad 对于世界坐标系中的三维点 ( X , Y , Z ) (X, Y, Z) (X,Y,Z),其在相机坐标系中的投影点 ( x , y ) (x, y) (x,y) 由以下方程描述:

畸变模型
\quad 镜头畸变通常会导致图像的几何失真,尤其是在图像边缘区域。常见的畸变有径向畸变和切向畸变。
径向畸变 ( R a d i a l D i s t o r t i o n ) (RadialDistortion) (RadialDistortion)
\quad 径向畸变通常由镜头的几何形状引起,影响图像中点到图像中心的距离。径向畸变的校正公式为:
x d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) x_d = x \left( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6 \right) + 2 p_1 xy + p_2 (r^2 + 2x^2) xd=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)
y d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y y_d = y \left( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6 \right) + p_1 (r^2 + 2y^2) + 2 p_2 xy yd=y(1+k1r2+k2r4+k3r6)+p1(r2+2y2)+2p2xy
\quad
其中,
\quad
(
r
2
=
x
2
+
y
2
)
( r^2 = x^2 + y^2 )
(r2=x2+y2) 是点到图像中心的平方距离,
\quad
(
p
1
,
p
2
,
k
1
,
k
2
,
k
3
)
( p_1, p_2, k_1, k_2, k_3 )
(p1,p2,k1,k2,k3) 是畸变系数,
\quad
(
x
,
y
)
(x, y)
(x,y) 是畸变前的图像坐标,
\quad
(
x
d
,
y
d
)
(x_d, y_d)
(xd,yd) 是畸变后的图像坐标。

切向畸变 ( T a n g e n t i a l D i s t o r t i o n ) (TangentialDistortion) (TangentialDistortion)
\quad 切向畸变是由于镜头与图像平面不完全平行造成的图像失真,通常用系数 ( p 1 ) ( p_1 ) (p1) 和 ( p 2 ) ( p_2 ) (p2) 来表示。
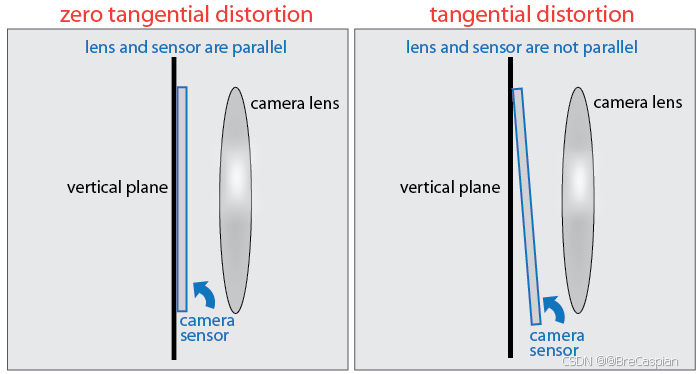
标定步骤(基于MATLAB与单目相机)
\quad 下面是完整的MATLAB标定步骤:

1. 标定板确认
\quad
张正友标定法要求使用一个平面的标定板,标定板上通常具有一个或多个已知尺寸的棋盘格图案。这个棋盘格图案需要在相机拍摄的过程中能被准确识别。通常,棋盘格的每个方块的尺寸是已知的,并且方块间的间距是均匀的。
\quad
这是实验室的标定板,每个小方块的大小50mm*50mm(这个数据在后续过程中需要使用)
\quad
另外建议不要使用亚克力类似的反射率较高的标定板(特别是在激光雷达与相机的联合标定中)

2. 拍摄标定板图像
\quad
使用相机从不同角度和位置拍摄标定板的多个图像。为了提高标定的准确性,标定板应该在视场范围内变化位置和姿态,使得图像包含尽可能多的棋盘角点。
\quad
需要注意的是:一定要保证拍摄的图片尺寸完全一致;移动相机或者标定板去拍摄不同视角的标定板图片(建议最少10张以上);相机或标定板位置并不固定可以自由移动,但要保证拍摄到完整的标定板(我这里稍微有点暗,不建议这样暗)
\quad
感谢小渠帮助我!她举了很久!


3. 角点提取
\quad 在拍摄的图像中提取棋盘格的角点。这些角点的二维坐标会用来计算相机的内参和外参。
\quad 对于每一组角点,假设该点的世界坐标是已知的(例如,棋盘格上角点的实际空间位置),其在图像中的投影位置通过以下公式进行映射:
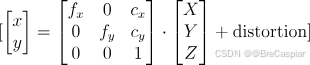
\quad
其中,
\quad
(
x
,
y
)
(x, y)
(x,y)是图像中的点坐标,
\quad
(
X
,
Y
,
Z
)
(X, Y, Z)
(X,Y,Z)是世界坐标中的点,
\quad
(
f
x
,
f
y
)
(f_x, f_y)
(fx,fy)是焦距,
\quad
(
c
x
,
c
y
)
(c_x, c_y)
(cx,cy)是主点坐标,
\quad
畸变项表示相机的非理想效应。
\quad 下面是MATLAB中的自动角点提取
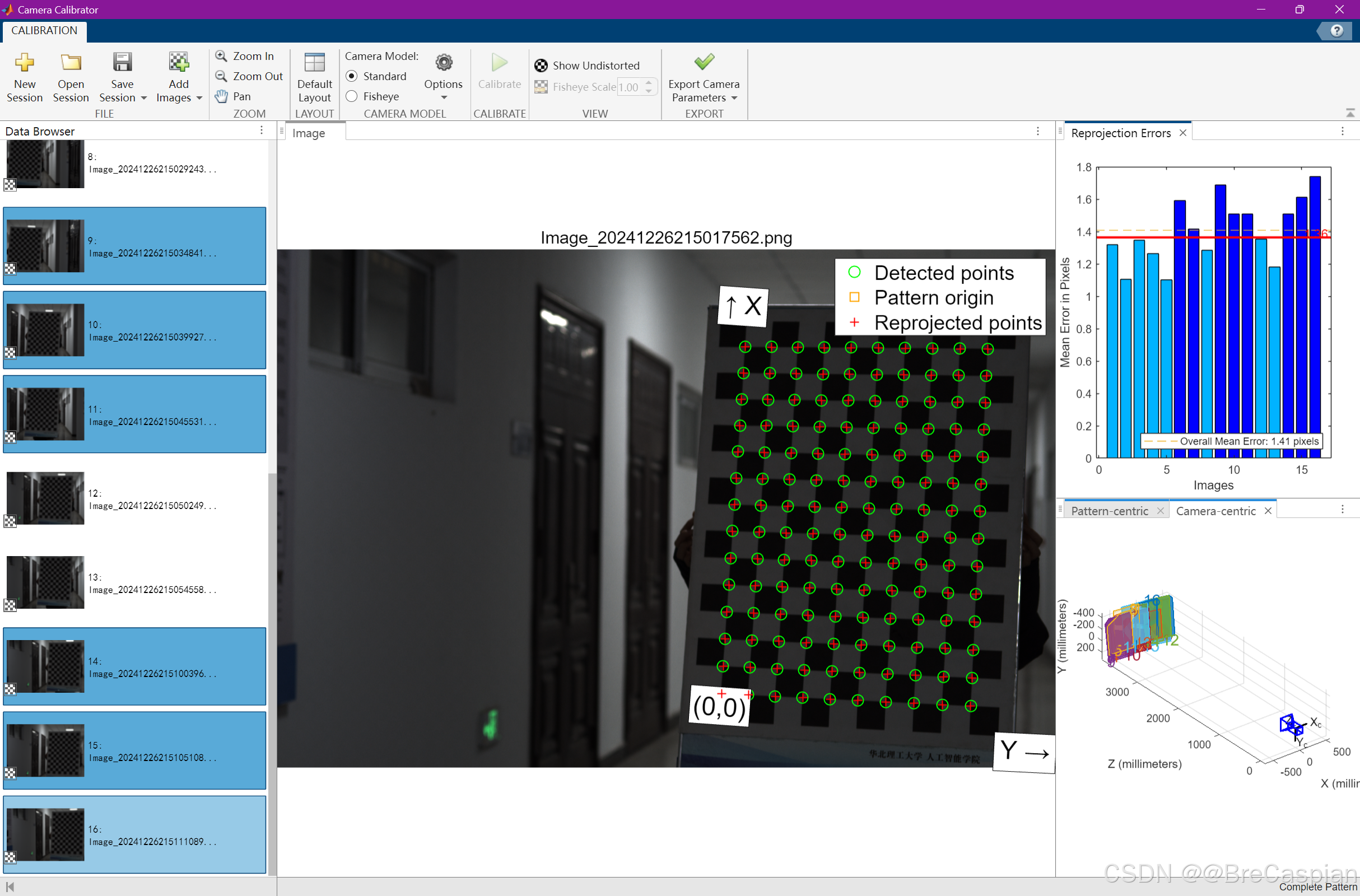
4. 最小化重投影误差
\quad 对于每一组角点,我们有一组已知的三维世界坐标 ( X , Y , Z ) (X, Y, Z) (X,Y,Z) 和二维图像坐标 ( x , y ) (x, y) (x,y)。通过相机模型,将三维点投影到图像平面上的点 ( x ′ , y ′ ) (x', y') (x′,y′),并计算重投影误差:
e i = ( x i ′ − x i ) 2 + ( y i ′ − y i ) 2 e_i = \sqrt{(x_i' - x_i)^2 + (y_i' - y_i)^2} ei=(xi′−xi)2+(yi′−yi)2
\quad 其中, ( e i ) ( e_i ) (ei) 是第 ( i ) ( i ) (i)个角点的重投影误差。
\quad 上述计算MATLAB将会自动完成
\quad 这里只需要选择到一半即0.5便可(平均误差)
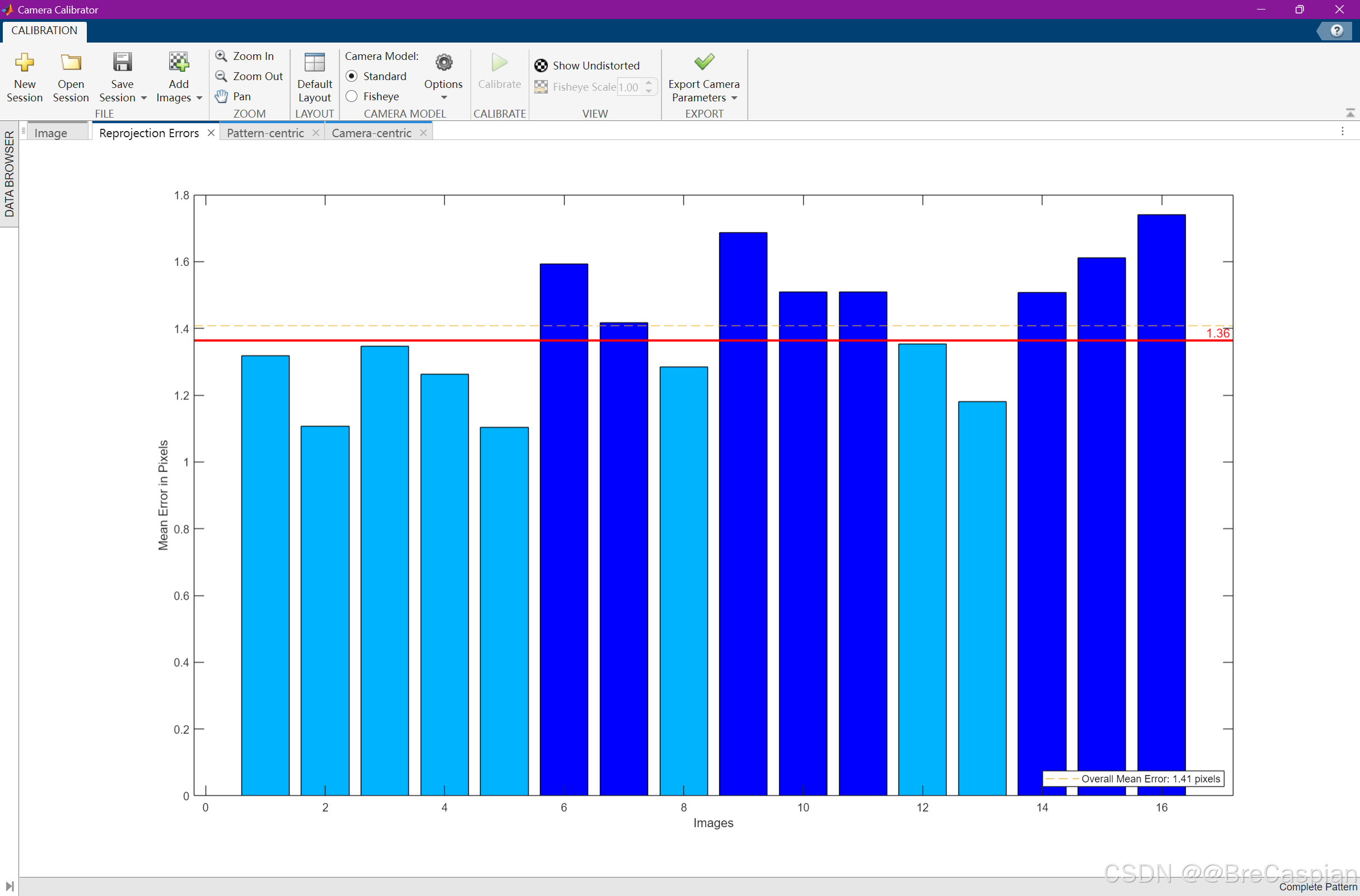
5. 优化内外参
\quad 基于上述数学模型,使用非线性最小二乘法(例如 L e v e n b e r g − M a r q u a r d t Levenberg-Marquardt Levenberg−Marquardt算法)来最小化重投影误差,从而求解相机的内参和外参。重投影误差是指通过相机模型将三维点投影到图像平面后,与实际图像中的角点位置之间的差异。
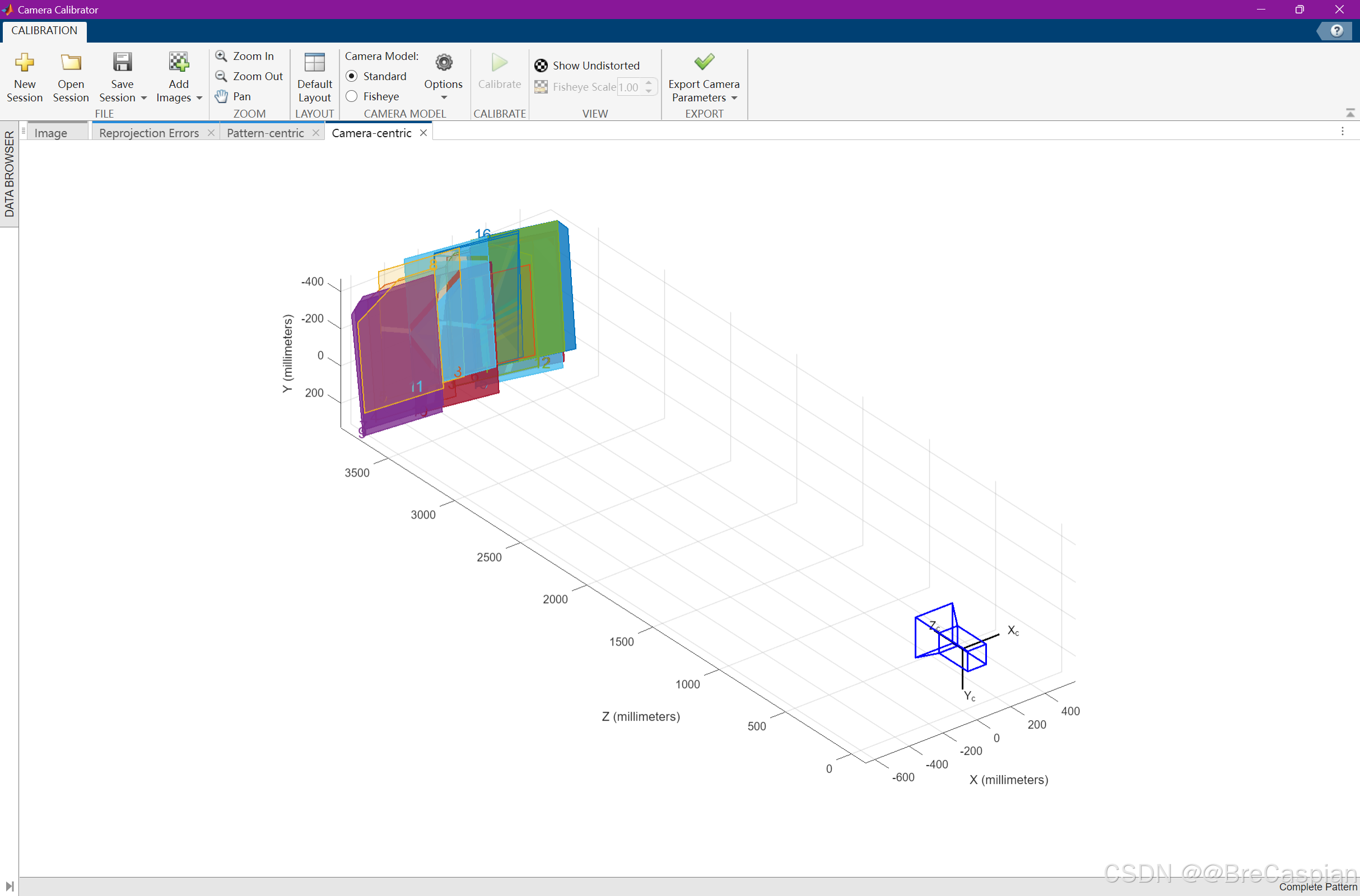
\quad 在实际应用中,镜头畸变(例如径向畸变和切向畸变)会导致图像中的几何畸变。因此,张正友标定法通常也会估计这些畸变系数,并将其纳入到优化过程。
\quad 在MATLAB中完成如上步骤便可自动推算出相关参数并直接导出相机的内参、外参以及估计误差,可以在MATLAB的WORKSPACE中直接查看。
导出参数详解
\quad 我使用的是海康威视单目工业相机搭配长焦镜头,下面是我的相机参数:

\quad
这些是 MATLAB 中 cameraParameters 和 cameraCalibrationErrors对象的输出属性,主要用于描述通过相机标定过程估计出的相机内参
I
n
t
r
i
n
s
i
c
P
a
r
a
m
e
t
e
r
s
Intrinsic Parameters
IntrinsicParameters和外参
E
x
t
r
i
n
s
i
c
P
a
r
a
m
e
t
e
r
s
Extrinsic Parameters
ExtrinsicParameters,以及它们的估计误差。
1. cameraParams - 相机标定结果对象
\quad cameraParams是 MATLAB 中用于存储相机标定结果的对象,包含了相机标定过程中估计的各种参数,包括内参、外参、估计精度等。
\quad Camera Intrinsics (相机内参)
\quad 相机的内参 i n t r i n s i c s intrinsics intrinsics定义了相机的成像模型。它主要包括:
\quad
焦距
(
f
x
)
( f_x )
(fx),
(
f
y
)
( f_y )
(fy):相机的焦距,表示成像平面上一个像素的物理尺寸。焦距通常与相机的传感器尺寸和图像分辨率相关。
\quad
主点
(
c
x
)
( c_x )
(cx),
(
c
y
)
( c_y )
(cy):主点是图像坐标系的原点,通常是图像的中心点。实际情况下,主点不一定位于图像的几何中心,尤其是在非理想的相机中。
\quad
畸变系数:镜头的畸变,如径向畸变和切向畸变,通常会影响图像的几何形状。
\quad 在标定过程中,使用标定板上的已知三维世界坐标和其在图像中的投影,来估计这些内参。

\quad 这里的矩阵 K K K 是相机的内参矩阵,其中:
\quad
f
x
f_x
fx 和
f
y
f_y
fy 是焦距。
\quad
c
x
c_x
cx 和
c
y
c_y
cy 是主点的图像坐标。
\quad
1
1
1 是齐次坐标的标量。
\quad Camera Extrinsics (相机外参)
\quad 相机的外参 ( e x t r i n s i c s ) (extrinsics) (extrinsics)描述了相机与世界坐标系之间的关系,主要包括:
\quad
旋转矩阵
(
R
)
( R )
(R):表示从世界坐标系到相机坐标系的旋转变换。
\quad
平移向量
(
T
)
( T )
(T):表示从世界坐标系原点到相机坐标系原点的平移量。
\quad 在标定中,相机外参通过将标定板上的已知三维点与图像中的投影点进行匹配来估计。外参可以用来描述世界坐标系中的点是如何投影到相机坐标系中,或者反向描述相机的位置和姿态。
\quad 外参的一般形式为:

\quad 其中:
\quad
(
X
,
Y
,
Z
)
(X, Y, Z)
(X,Y,Z) 是世界坐标系中的点。
\quad
(
x
,
y
,
z
)
(x, y, z)
(x,y,z) 是相机坐标系中的点。
\quad
(
R
)
( R )
(R) 是旋转矩阵,描述相机坐标系相对于世界坐标系的旋转。
\quad
(
T
)
( T )
(T) 是平移向量,描述相机坐标系原点与世界坐标系原点之间的平移。
\quad Accuracy of Estimation (估计精度)
\quad 估计精度用于评估相机标定的质量。最常用的精度指标是重投影误差。重投影误差描述了标定过程中计算出的3D点在图像平面中的投影与实际测量的图像点之间的差异。重投影误差越小,表示相机标定越精确。
\quad MeanReprojectionError:这是所有标定图像中的平均重投影误差。如:
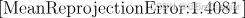
\quad 这表示标定结果的平均误差为1.4081像素。该值越小,说明标定结果越准确。
\quad ReprojectionErrors:这是一个三维矩阵,表示每个角点在每张图像中的重投影误差。它通常是一个 ( 140 × 2 × 16 ) ( 140 \times 2 \times 16 ) (140×2×16) 的矩阵,包含每张图像中的每个角点的 ( x ) ( x ) (x) 和 ( y ) ( y ) (y) 方向的误差。
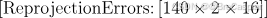
\quad ReprojectedPoints:这也是一个三维矩阵,包含使用标定得到的相机内外参重新投影的三维世界坐标点在图像中的位置。
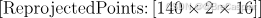
\quad Calibration Settings (标定设置)
\quad 标定设置提供了标定过程中的一些基本配置,包括使用的图案数量、是否估计偏斜系数、是否估计畸变等。
\quad NumPatterns:表示用于标定的图案数量。在该案例中,标定图像数量为16。

\quad DetectedKeypoints:是一个逻辑矩阵,表示每个图像中是否成功检测到角点。如:
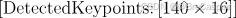
\quad 这个矩阵的每个元素为 1 或 0,表示在该图像中对应角点是否被检测到。
\quad WorldPoints:是一个矩阵,包含每个角点在世界坐标系中的坐标。

\quad WorldUnits:世界坐标系中的单位,通常为毫米或米。
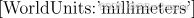
\quad EstimateSkew:表示是否估计偏斜系数。通常情况下,偏斜系数是0,即图像坐标轴是正交的。

\quad NumRadialDistortionCoefficients:表示估计的径向畸变系数的数量。常见的径向畸变模型包含2或3个系数。
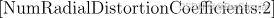
\quad EstimateTangentialDistortion:表示是否估计切向畸变。切向畸变通常由镜头的制造误差或安装误差引起。
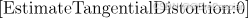
2. cameraCalibrationErrors - 标定误差对象
\quad c a m e r a C a l i b r a t i o n E r r o r s cameraCalibrationErrors cameraCalibrationErrors对象包含了相机标定过程中的误差估计信息,主要用于评估内参和外参的准确性。
\quad IntrinsicsErrors (内参误差)
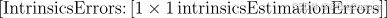
\quad 这个对象包含了内参的估计误差,通常包括每个内参(如焦距、主点、畸变系数)的误差。如果误差较大,说明这些参数的估计可能不够准确,可能需要改进标定过程。
\quad ExtrinsicsErrors (外参误差)
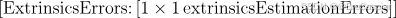
\quad
这个对象包含了外参(旋转矩阵和平移向量)的估计误差。外参误差描述了标定图像中的每个角点的三维世界坐标与图像坐标系中重投影坐标之间的误差。
\quad
标定误差的评估有助于判断标定是否成功,以及标定结果的可靠性。
具体输出参数详解
在获得上述输出以后,我们在输出参数的下方分别输入
—>
\quad
c
a
m
e
r
a
P
a
r
a
m
s
.
I
n
t
r
i
n
s
i
c
M
a
t
r
i
x
cameraParams.IntrinsicMatrix
cameraParams.IntrinsicMatrix
—>
\quad
c
a
m
e
r
a
P
a
r
a
m
s
.
R
a
d
i
a
l
D
i
s
t
o
r
t
i
o
n
cameraParams.RadialDistortion
cameraParams.RadialDistortion
—>
\quad
c
a
m
e
r
a
P
a
r
a
m
s
.
T
a
n
g
e
n
t
i
a
l
D
i
s
t
o
r
t
i
o
n
cameraParams.TangentialDistortion
cameraParams.TangentialDistortion
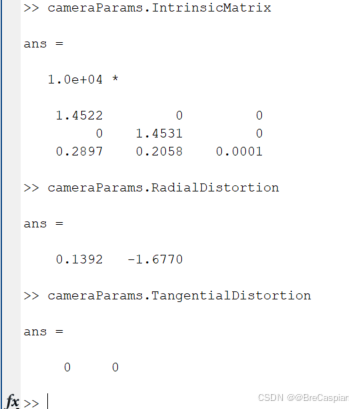
\quad 输入后便可分别得到如下参数,下面是我的相机参数:
\quad
I
n
t
r
i
n
s
i
c
M
a
t
r
i
x
IntrinsicMatrix
IntrinsicMatrix: 相机的内参矩阵,包含焦距和光心位置。
\quad
R
a
d
i
a
l
D
i
s
t
o
r
t
i
o
n
Radial Distortion
RadialDistortion: 径向畸变参数,描述镜头的几何畸变。
\quad
T
a
n
g
e
n
t
i
a
l
D
i
s
t
o
r
t
i
o
n
Tangential Distortion
TangentialDistortion: 切向畸变参数,通常描述镜头与图像平面的不完全对准。
1. 内参矩阵 ( I n t r i n s i c M a t r i x ) (IntrinsicMatrix) (IntrinsicMatrix)
\quad c a m e r a P a r a m s . I n t r i n s i c M a t r i x cameraParams.IntrinsicMatrix cameraParams.IntrinsicMatrix 是相机的内参矩阵,它描述了相机的内部特性(如焦距、光心位置等)。这个矩阵的形式通常是:

其中:
\quad
(
f
x
)
( f_x )
(fx) 和
(
f
y
)
( f_y )
(fy) 是相机的焦距(以像素为单位)。通常,这两个值非常相近,因为大多数相机的焦距在水平和垂直方向上是相同的。
\quad
(
c
x
)
( c_x )
(cx) 和
(
c
y
)
( c_y )
(cy) 是光心的坐标(通常是图像的中心点)。
\quad
最后一行是固定的
[
0
,
0
,
1
]
[0, 0, 1]
[0,0,1]。
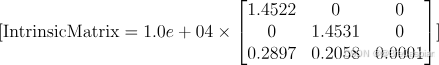
\quad
意味着焦距
(
f
x
=
1.4522
×
1
0
4
)
( f_x = 1.4522 \times 10^4 )
(fx=1.4522×104) 像素 和
(
f
y
=
1.4531
×
1
0
4
)
( f_y = 1.4531 \times 10^4 )
(fy=1.4531×104) 像素,
\quad
光心的坐标是
(
c
x
,
c
y
)
=
(
0.2897
,
0.2058
)
(c_x, c_y) = (0.2897, 0.2058)
(cx,cy)=(0.2897,0.2058)。
\quad
这个矩阵是用来将三维世界坐标系中的点映射到二维图像坐标系中。
2. 径向畸变 ( R a d i a l D i s t o r t i o n ) (Radial Distortion) (RadialDistortion)
径向畸变通常由相机镜头的几何特性引起,会导致图像中的直线变形为弯曲的线。径向畸变通常由两个参数来表示,分别是 ( k 1 ) ( k_1 ) (k1) 和 ( k 2 ) ( k_2 ) (k2):
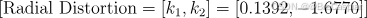
这两个参数描述了畸变的大小和类型:
(
k
1
)
( k_1 )
(k1) 和
(
k
2
)
( k_2 )
(k2) 分别表示径向畸变的一级和二级影响(通常用于补偿镜头的桶形或枕形畸变)。
(
k
1
=
0.1392
)
( k_1 = 0.1392 )
(k1=0.1392) 表示一定程度的桶形畸变(图像中心部分向外膨胀)。
(
k
2
=
−
1.6770
)
( k_2 = -1.6770 )
(k2=−1.6770) 表示图像可能有一定的枕形畸变(图像边缘部分向内拉伸)。
3. 切向畸变 ( T a n g e n t i a l D i s t o r t i o n ) (Tangential Distortion) (TangentialDistortion)
切向畸变通常是由镜头与图像平面不完全平行引起的,通常用两个参数来描述 ( p 1 ) ( p_1 ) (p1) 和 ( p 2 ) ( p_2 ) (p2):
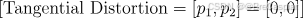
这表示切向畸变非常小,或者说可以忽略不计。在实际应用中,这些参数通常不会对图像的畸变产生显著影响,尤其是在现代相机中,切向畸变通常很小。
总结
\quad 现代计算机视觉库(如OpenCV)通常都实现了张正友标定法,只需要提供一系列拍摄的标定板图像和棋盘格的尺寸,库函数会自动进行标定。OpenCV中的 c v : : c a l i b r a t e C a m e r a ( ) cv::calibrateCamera() cv::calibrateCamera()就是实现这一方法的主要函数,能够同时估计相机的内参、外参和畸变系数。当然也可以在ROS/ROS2中进行实现,也可以进行仿真标定。
\quad 张正友标定法通过一组已知的标定板图像,使用棋盘格角点的二维坐标和已知的三维世界坐标,计算相机的内外参数。在标定过程中,需要考虑相机的畸变效应,并通过最小化重投影误差来优化结果。标定得到的参数可以用于各种计算机视觉任务,如三维重建、姿态估计等。
\quad 参考资料(感谢大佬,向大佬学习!)
\quad MATLAB相机标定
\quad 四大坐标系相互转换
\quad @ B r e C a s p i a n @BreCaspian @BreCaspian

评论记录:
回复评论: