❑ 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
❑ 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
例子：假设你要去野营。你有一个容量为6磅的背包，需要决定该携带下面的哪些东西。其中每样东西都有相应的价值，价值越大意味着越重要：
❑ 水（重3磅，价值10）；
❑ 书（重1磅，价值3）
❑ 食物（重2磅，价值9）；
❑ 夹克（重2磅，价值5）；
❑ 相机（重1磅，价值6）。
请问携带哪些东西时价值最高？
关键: 明确限制；明确最高价值。
| 重量（限制） | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 价值 | 0 | 0 | 10 | 10 | 10 | 10 |
| 价值 | 3 | 3 | 10 | 10 | 10 | 10 |
| 价值 | 3 | 9 | 12 | 12 | 19 | 22 |
| 价值 | 3 | 9 | 12 | 14 | 19 | 22 |
| 价值 | 6 | 9 | 15 | 16 | 19 | 25 |
注意：
（1）使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，而没法判断该不该拿走商品的一部分。
（2）横排顺序不影响。
最长公共子串（Longest Common Substring）是指在两个或多个字符串中具有相同字符序列的最长子串。与最长公共子序列（Longest Common Subsequence）不同，最长公共子串要求具有相同字符序列的子串在原字符串中的位置也是连续的。
当考虑字符串 “ABABC” 和 “BABCBA” 时，我们可以通过手动检查的方式来找到它们的最长公共子串。
String 1: A B A B C
String 2: B A B C B A
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">对齐两个字符串：
String 1: A B A B C
String 2: B A B C B A
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">从第一个字符开始，逐一比较对应位置的字符，直到遇到不相等的字符。
String 1: A B A B C
String 2: B A B C B A
^^^^^
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">找到最长公共子串 “BABC”。
通用算法：
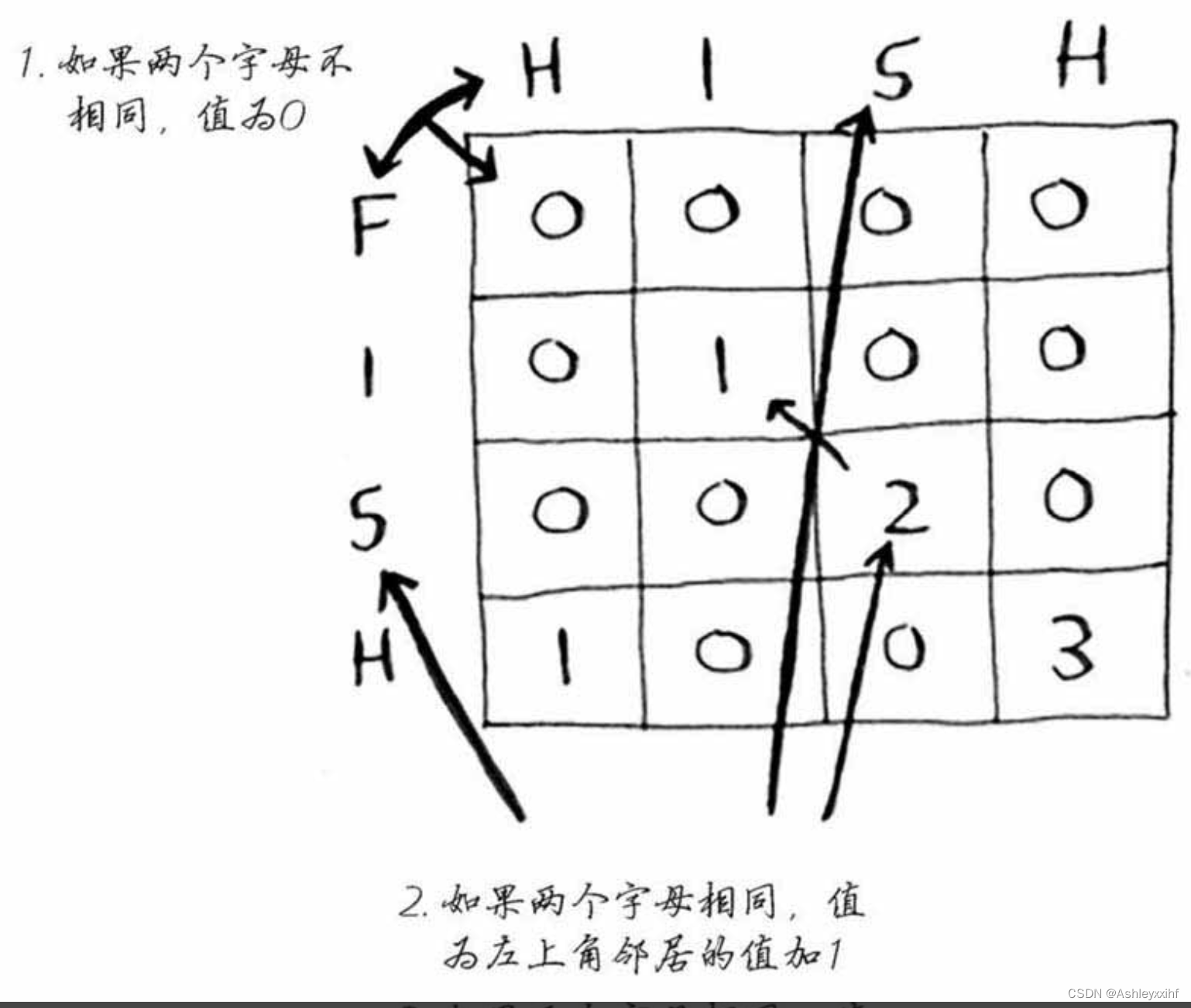
如果遇到相同值，就在在斜对角的值的基础上+1
if s1[i - 1] == s2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = 0
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
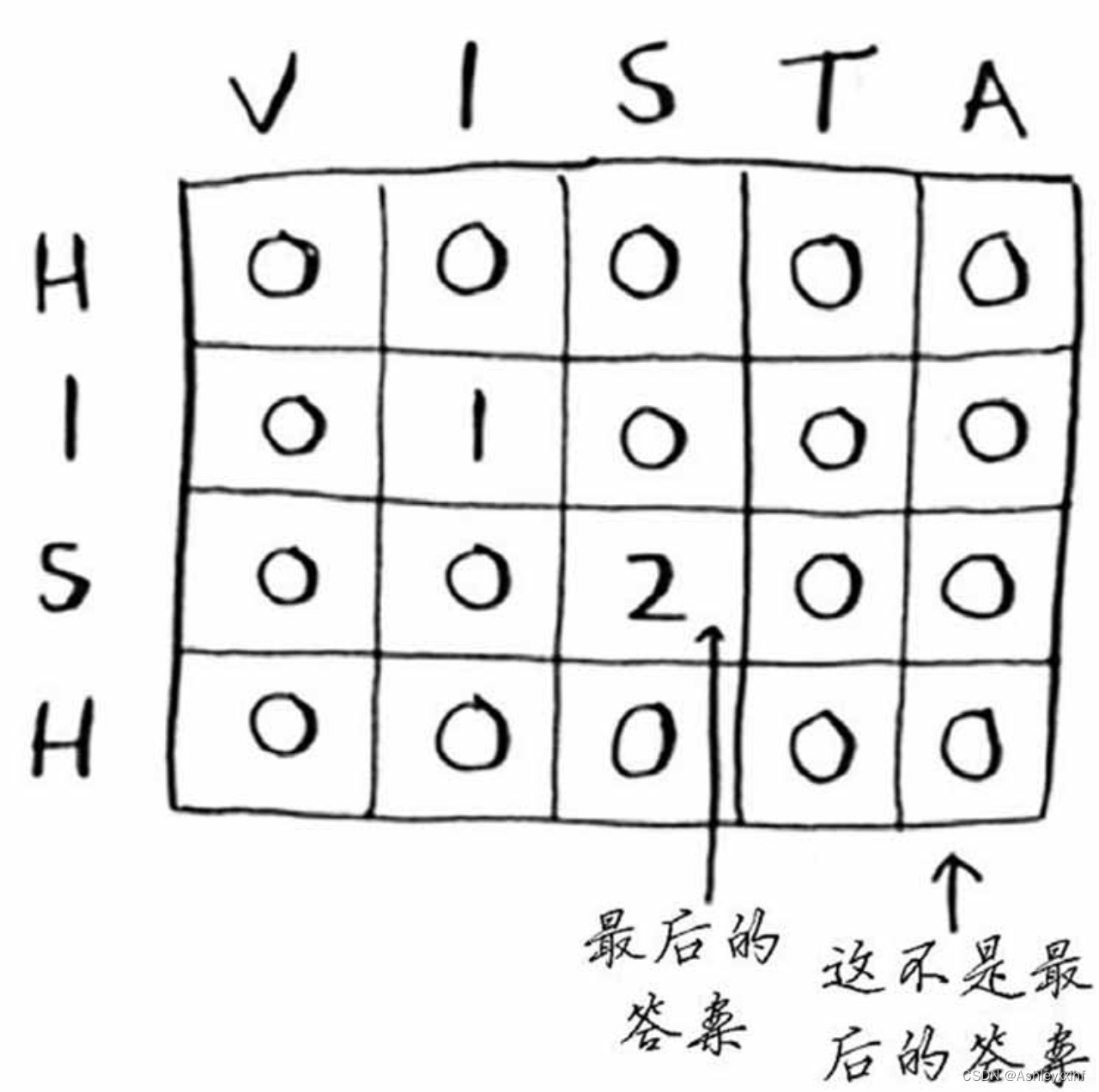
注意： 这个问题的最终答案并不在最后一个单元格中！对于前面的背包问题，最终答案总是在最后的单元格中。但对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中。
最长公共子序列（Longest Common Subsequence，简称 LCS）指在两个或多个字符串中，以相同的顺序出现，但不一定连续的字符序列。LCS 可以跳过字符位置，但要保持相对顺序。
举例，考虑字符串 “ABCD” 和 “ACDF”，它们的最长公共子序列是 “ACD”。在这个子序列中，字符的相对顺序是相同的，但不要求是连续的。
通用：
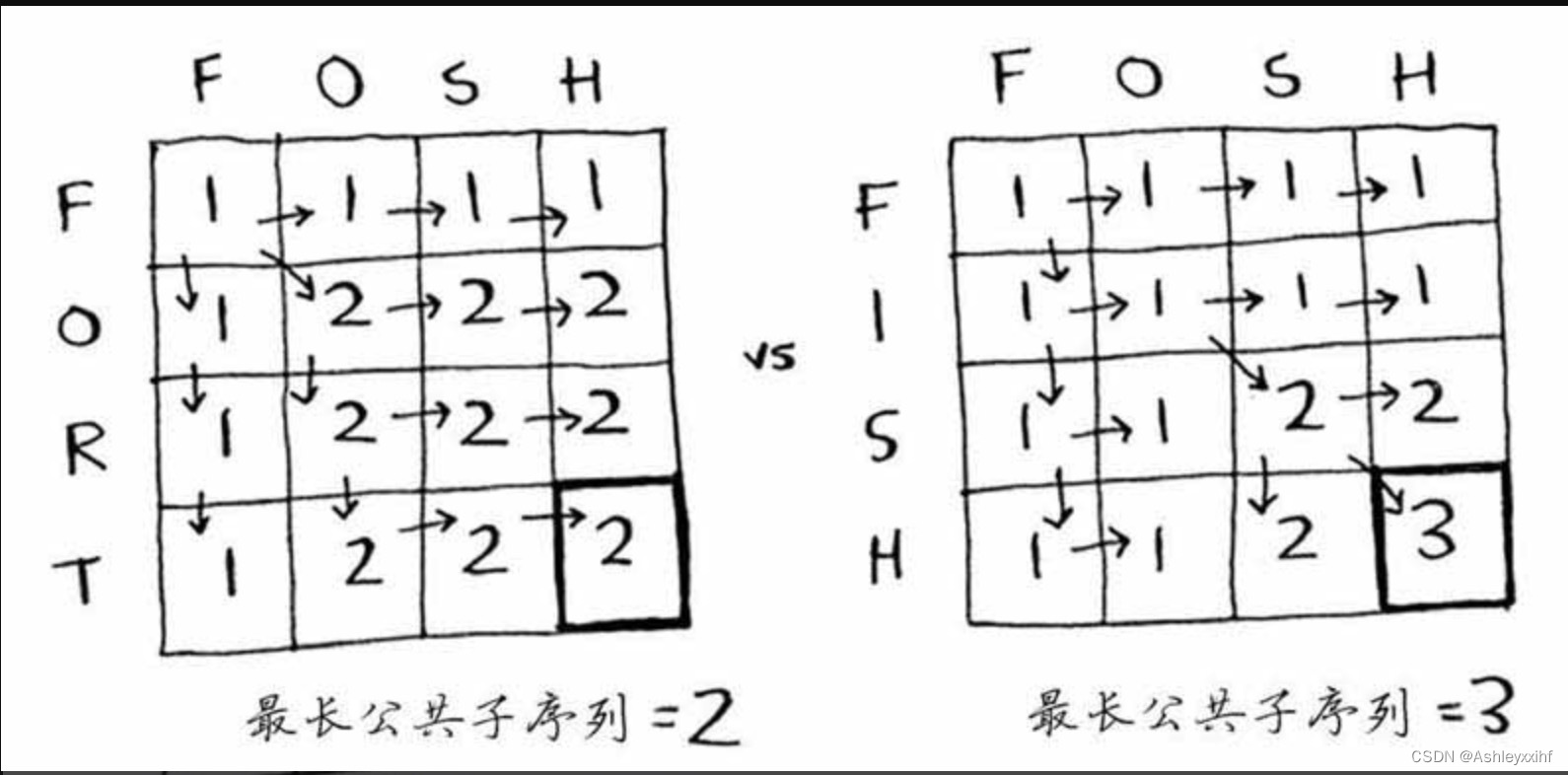
如果字母相同，对角线斜上方+1.
如果字母不同，选择上方和左上邻居比较大的那个。
if s1[i - 1] == s2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
❑ 需要在给定约束条件下优化某种指标时，动态规划很有用。
❑ 问题可分解为离散子问题时，可使用动态规划来解决。
❑ 每种动态规划解决方案都涉及网格。
❑ 单元格中的值通常就是你要优化的值。
❑ 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
❑ 没有放之四海皆准的计算动态规划解决方案的公式。
评论记录：
回复评论：