【LeetCode】力扣刷题热题100道（31-35题）附源码 搜索二维矩阵 岛屿数量 腐烂的橙子 课程表 实现 Trie (前缀树)（C++）

一、搜索二维矩阵

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

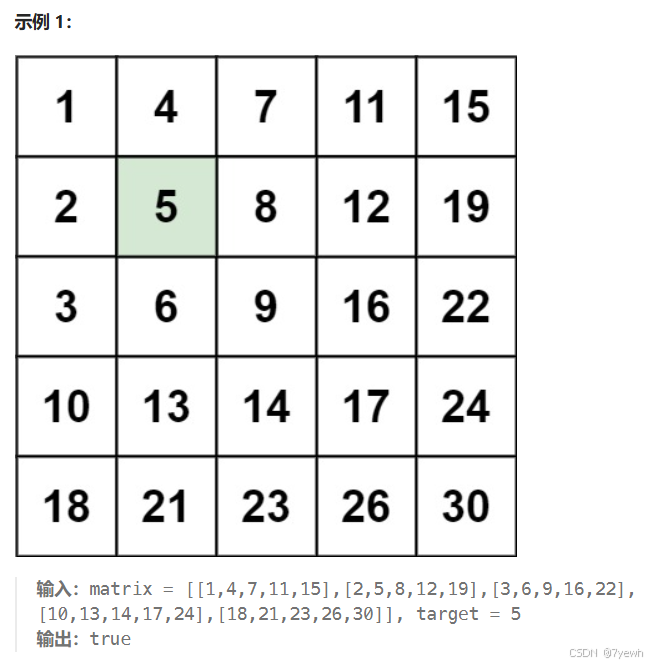
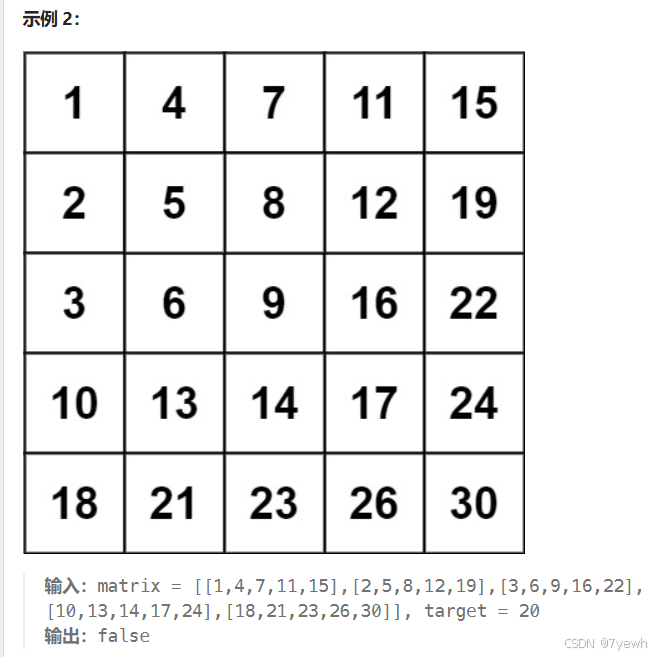
可以使用 从右上角开始搜索 的方法来有效地找到目标值。

  1. 选择起始位置： 从矩阵的右上角开始。假设我们当前的位置是 matrix[0][n-1]，其中 n 是列数。
  2. 逐步搜索：
    • 如果当前元素等于目标值，返回 true。
    • 如果当前元素大于目标值，说明目标值可能出现在当前元素的左边，因此我们向左移动一列。
    • 如果当前元素小于目标值，说明目标值可能出现在当前元素的下方，因此我们向下移动一行。
  3. 结束条件： 如果超出了矩阵的边界，说明没有找到目标值，返回 false。
  1. class Solution {
  2. public:
  3.     bool searchMatrix(vectorint>>& matrix, int target) {
  4.         if (matrix.empty() || matrix[0].empty()) return false;
  5.  
  6.         int m = matrix.size();     // 行数
  7.         int n = matrix[0].size();  // 列数
  8.         
  9.         // 从右上角开始
  10.         int row = 0;
  11.         int col = n - 1;
  12.  
  13.         while (row < m && col >= 0) {
  14.             if (matrix[row][col] == target) {
  15.                 return true;  // 找到目标值
  16.             } else if (matrix[row][col] > target) {
  17.                 col--;  // 当前元素大于目标值，向左移动
  18.             } else {
  19.                 row++;  // 当前元素小于目标值，向下移动
  20.             }
  21.         }
  22.         
  23.         return false;  // 没有找到目标值
  24.     }
  25. };
  • 初始位置：从矩阵的右上角 matrix[0][n-1] 开始。
  • 移动规则：
    • 如果当前元素等于目标值，则返回 true。
    • 如果当前元素大于目标值，则移动到左边一列。
    • 如果当前元素小于目标值，则移动到下方一行。
  • 边界条件：当行数或列数超出范围时，结束搜索。

二、岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

  • DFS 遍历：从每个尚未访问的陆地单元格开始，使用 DFS 遍历其所有相邻的陆地单元格，将它们标记为已访问。每次发现一个新的未被访问的陆地，就说明发现了一个新的岛屿。

  • 标记访问：为了避免重复计算同一个岛屿，需要在遍历过程中将已经访问过的陆地标记为水（'0'），这样就不会再次访问到它。

  • 岛屿计数：每当我们从一个未访问的陆地开始 DFS 时，岛屿数加一。

  • 对于每一个格子，如果它是陆地 ('1') 且未被访问，则从该格子开始进行 DFS，将与之相连的所有陆地格子标记为已访问，并将岛屿数量加一。
  • 遍历所有格子，最终得到岛屿的数量。
  • 对于一个陆地格子（'1'），递归地向上下左右四个方向扩展，找到与它相连的所有陆地并将其标记为水（'0'）。
  • 这样做的目的是确保每个岛屿的陆地只被计数一次。
  1. class Solution {
  2. public:
  3.     void dfs(vectorchar>>& grid, int i, int j) {
  4.         // 边界条件：如果当前格子越界或已经是水（'0'），则返回
  5.         if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] == '0') {
  6.             return;
  7.         }
  8.         
  9.         // 将当前陆地格子标记为水，表示已访问
  10.         grid[i][j] = '0';
  11.         
  12.         // 递归四个方向
  13.         dfs(grid, i + 1, j);  // 向下
  14.         dfs(grid, i - 1, j);  // 向上
  15.         dfs(grid, i, j + 1);  // 向右
  16.         dfs(grid, i, j - 1);  // 向左
  17.     }
  18.     
  19.     int numIslands(vectorchar>>& grid) {
  20.         if (grid.empty()) return 0;
  21.         
  22.         int numIslands = 0;
  23.         
  24.         // 遍历整个网格
  25.         for (int i = 0; i < grid.size(); ++i) {
  26.             for (int j = 0; j < grid[0].size(); ++j) {
  27.                 // 找到一个未访问的陆地，启动 DFS
  28.                 if (grid[i][j] == '1') {
  29.                     numIslands++;  // 发现新的岛屿
  30.                     dfs(grid, i, j);  // 使用 DFS 标记整个岛屿
  31.                 }
  32.             }
  33.         }
  34.         
  35.         return numIslands;
  36.     }
  37. };

  • DFS 函数：dfs 用来递归访问与当前格子相连的所有陆地格子，并将它们标记为水（'0'）。

    • 参数 i, j 表示当前正在处理的格子坐标。
    • 在函数内部，首先检查是否越界或是否已经是水（'0'），如果是则直接返回。
    • 然后标记当前格子为水，并递归检查四个方向（上下左右）。

  • 主函数：numIslands 遍历整个二维网格，发现每个未访问的陆地时，调用 dfs 来标记所有相连的陆地，从而确保每个岛屿只计算一次。

  • 边界条件：如果网格为空，直接返回 0。

三、腐烂的橙子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

 

  1. class Solution {
  2. public:
  3.     int orangesRotting(vectorint>>& grid) {
  4.         int m = grid.size();
  5.         int n = grid[0].size();
  6.         
  7.         // 记录腐烂的橘子的位置
  8.         queueint, int>> rotten;
  9.         int freshCount = 0;  // 记录新鲜橘子的数量
  10.         
  11.         // 初始化队列和新鲜橘子数量
  12.         for (int i = 0; i < m; ++i) {
  13.             for (int j = 0; j < n; ++j) {
  14.                 if (grid[i][j] == 2) {
  15.                     rotten.push({i, j});
  16.                 } else if (grid[i][j] == 1) {
  17.                     freshCount++;
  18.                 }
  19.             }
  20.         }
  21.         
  22.         // 如果没有新鲜橘子，直接返回 0
  23.         if (freshCount == 0) return 0;
  24.         
  25.         // 四个方向
  26.         vectorint, int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
  27.         
  28.         int minutes = 0;
  29.         
  30.         // 开始 BFS
  31.         while (!rotten.empty()) {
  32.             int size = rotten.size();
  33.             bool rottedThisRound = false;  // 记录这一轮是否有橘子腐烂
  34.             
  35.             for (int i = 0; i < size; ++i) {
  36.                 auto [x, y] = rotten.front();
  37.                 rotten.pop();
  38.                 
  39.                 // 四个方向扩展
  40.                 for (auto& dir : directions) {
  41.                     int nx = x + dir.first;
  42.                     int ny = y + dir.second;
  43.                     
  44.                     // 如果新位置在网格内且是新鲜橘子
  45.                     if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == 1) {
  46.                         grid[nx][ny] = 2;  // 将新鲜橘子腐烂
  47.                         rotten.push({nx, ny});  // 加入队列
  48.                         freshCount--;  // 减少新鲜橘子的数量
  49.                         rottedThisRound = true;
  50.                     }
  51.                 }
  52.             }
  53.             
  54.             // 如果这一轮有橘子腐烂，时间增加
  55.             if (rottedThisRound) {
  56.                 minutes++;
  57.             }
  58.         }
  59.         
  60.         // 如果还有新鲜橘子，返回 -1
  61.         return freshCount == 0 ? minutes : -1;
  62.     }
  63. };
  • 初始化：
    • 我们先遍历网格，找到所有腐烂的橘子，并将其加入队列。同时，我们统计新鲜橘子的数量。
  • BFS 过程：
    • 我们从腐烂的橘子开始，逐层扩展，检查每个腐烂橘子周围的四个方向。
    • 如果发现相邻位置是新鲜橘子（值为 1），我们就把它变成腐烂的橘子（值改为 2），并将其加入队列，继续扩展。
    • 每次扩展都意味着时间增加一分钟。
  • 结束条件：
    • 如果在 BFS 完成后还有新鲜橘子（freshCount > 0），说明不能完全腐烂所有橘子，返回 -1。
    • 否则，返回所需的分钟数。

四、课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。

  • 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

  1. class Solution {
  2. public:
  3.     bool canFinish(int numCourses, vectorint>>& prerequisites) {
  4.         vector<int> indegree(numCourses, 0);  // 记录每个课程的入度
  5.         vectorint>> graph(numCourses);  // 邻接表表示图
  6.         
  7.         // 构建图和入度数组
  8.         for (const auto& prereq : prerequisites) {
  9.             int course = prereq[0];  // 需要学习的课程
  10.             int pre = prereq[1];     // 先修课程
  11.             graph[pre].push_back(course);  // 将 course 加入 pre 的邻接表
  12.             indegree[course]++;  // course 的入度加 1
  13.         }
  14.         
  15.         // 使用队列存储入度为 0 的课程
  16.         queue<int> q;
  17.         for (int i = 0; i < numCourses; ++i) {
  18.             if (indegree[i] == 0) {
  19.                 q.push(i);  // 将入度为 0 的课程加入队列
  20.             }
  21.         }
  22.         
  23.         int count = 0;  // 记录已修课程的数量
  24.         while (!q.empty()) {
  25.             int course = q.front();
  26.             q.pop();
  27.             count++;
  28.             
  29.             // 对当前课程的所有后续课程（即它的邻接课程）进行处理
  30.             for (int nextCourse : graph[course]) {
  31.                 indegree[nextCourse]--;  // 当前课程修完，减去下一个课程的入度
  32.                 if (indegree[nextCourse] == 0) {
  33.                     q.push(nextCourse);  // 如果下一个课程的入度为 0，加入队列
  34.                 }
  35.             }
  36.         }
  37.         
  38.         // 如果修完的课程数量等于总课程数，则可以完成所有课程
  39.         return count == numCourses;
  40.     }
  41. };
  • 构建图和入度数组：
    • 我们首先创建一个 graph 数组来存储图的邻接表，并创建一个 indegree 数组来记录每个课程的入度（即每个课程有多少先修课程）。
    • 然后，我们根据 prerequisites 数组来构建图，并更新每个课程的入度。
  • 拓扑排序：
    • 我们初始化一个队列 q，将所有入度为 0 的课程加入队列。
    • 逐个从队列中取出课程，修完后，将它的邻接课程的入度减 1。如果某个邻接课程的入度变为 0，则将它加入队列。
  • 判断是否完成所有课程：
    • 最后，我们检查已修的课程数量 count 是否等于总课程数 numCourses。如果相等，说明没有环路，返回 true；否则，返回 false。

五、实现 Trie (前缀树)

Trie（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补全和拼写检查。

请你实现 Trie 类：

  • Trie() 初始化前缀树对象。
  • void insert(String word) 向前缀树中插入字符串 word 。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

  1. class Trie {
  2. private:
  3.     struct TrieNode {
  4.         unordered_map<char, TrieNode*> children;
  5.         bool isWord;
  6.         
  7.         TrieNode() : isWord(false) {}
  8.     };
  9.     
  10.     TrieNode* root;
  11.  
  12. public:
  13.     // 构造函数，初始化 Trie 树
  14.     Trie() {
  15.         root = new TrieNode();
  16.     }
  17.     
  18.     // 向 Trie 插入一个字符串
  19.     void insert(string word) {
  20.         TrieNode* node = root;
  21.         for (char c : word) {
  22.             // 如果当前字符的子节点不存在，则创建一个新的节点
  23.             if (node->children.find(c) == node->children.end()) {
  24.                 node->children[c] = new TrieNode();
  25.             }
  26.             node = node->children[c];
  27.         }
  28.         // 标记字符串结束的节点
  29.         node->isWord = true;
  30.     }
  31.     
  32.     // 查找字符串是否存在于 Trie 中
  33.     bool search(string word) {
  34.         TrieNode* node = root;
  35.         for (char c : word) {
  36.             if (node->children.find(c) == node->children.end()) {
  37.                 return false;  // 如果有字符没有找到对应节点，返回 false
  38.             }
  39.             node = node->children[c];
  40.         }
  41.         // 如果到达字符串结尾并且是一个完整的单词，返回 true
  42.         return node->isWord;
  43.     }
  44.     
  45.     // 检查是否有任何单词以 prefix 为前缀
  46.     bool startsWith(string prefix) {
  47.         TrieNode* node = root;
  48.         for (char c : prefix) {
  49.             if (node->children.find(c) == node->children.end()) {
  50.                 return false;  // 如果有字符没有找到对应节点，返回 false
  51.             }
  52.             node = node->children[c];
  53.         }
  54.         // 如果遍历完整个前缀，说明 Trie 中有以 prefix 为前缀的单词
  55.         return true;
  56.     }
  57. };
  58.  
  59. /**
  60.  * Your Trie object will be instantiated and called as such:
  61.  * Trie* obj = new Trie();
  62.  * obj->insert(word);
  63.  * bool param_2 = obj->search(word);
  64.  * bool param_3 = obj->startsWith(prefix);
  65.  */

  • TrieNode 结构体：每个 TrieNode 代表一个树节点，包含：

    • children：一个哈希表，键是字符，值是指向子节点的指针。这个哈希表用于存储当前节点的所有子节点。
    • isWord：一个布尔值，标记当前节点是否为一个单词的结束。

  • Trie 构造函数：创建一个空的根节点 root。

  • insert(word)：

    • 从根节点开始，逐个字符遍历 word。
    • 如果某个字符的子节点不存在，则创建一个新的子节点。
    • 最后，将最后一个字符的 isWord 标记为 true，表示这是一个完整的单词。

  • search(word)：

    • 从根节点开始，逐个字符遍历 word。
    • 如果在任何字符位置找不到对应的子节点，则返回 false。
    • 如果遍历结束并且当前节点的 isWord 为 true，说明找到了该单词，返回 true。

  • startsWith(prefix)：

    • 从根节点开始，逐个字符遍历 prefix。
    • 如果在某个字符位置找不到对应的子节点，则返回 false。
    • 如果能够遍历完前缀的所有字符，说明存在以该前缀为开始的单词，返回 true。
商务合作/咨询/联系我
微信名片
注：本文转载自blog.csdn.net的7yewh的文章"https://blog.csdn.net/weixin_64593595/article/details/145141328"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！