数学|数学建模——层次分析法（AHP）

层次分析法的缘由

层次分析法（AHP）是由美国运筹学家托马斯·塞蒂（T. L. Saaty）在20世纪70年代提出的。

当时，在进行复杂的社会、经济等系统决策问题时，需要综合考虑多种因素，这些因素往往相互关联、相互制约，很难用传统的数学模型去简单处理。塞蒂教授为了将复杂的决策问题层次化，把一个复杂问题分解成多个组成因素，并将这些因素按支配关系分组形成递阶层次结构，通过构建判断矩阵、计算权重向量等步骤，为决策者提供一种系统、实用的多准则决策方法，于是层次分析法应运而生。

层次分析法，就是把一个复杂的的问题拆解为多个层次，例如：目标层、准则层、方案层。然后通过对比因素重要性，确定权重，再综合评估得出最优方案。该方法将定量分析和定性分析结合起来，用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用全数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题。

层次分析法的三大典型应用

（1）用于最佳方案的选取

（2）用于评价类问题

（3）用于指标体系的优选

运用层次分析法构造系统模型

（1）建立层次结构模型

（2）构造判断（成对比较）矩阵

（3）层次单排序及其一致性检验

（4）层次总排序及其一致性检验

层次分析法的具体流程

一、建立层次结构模型

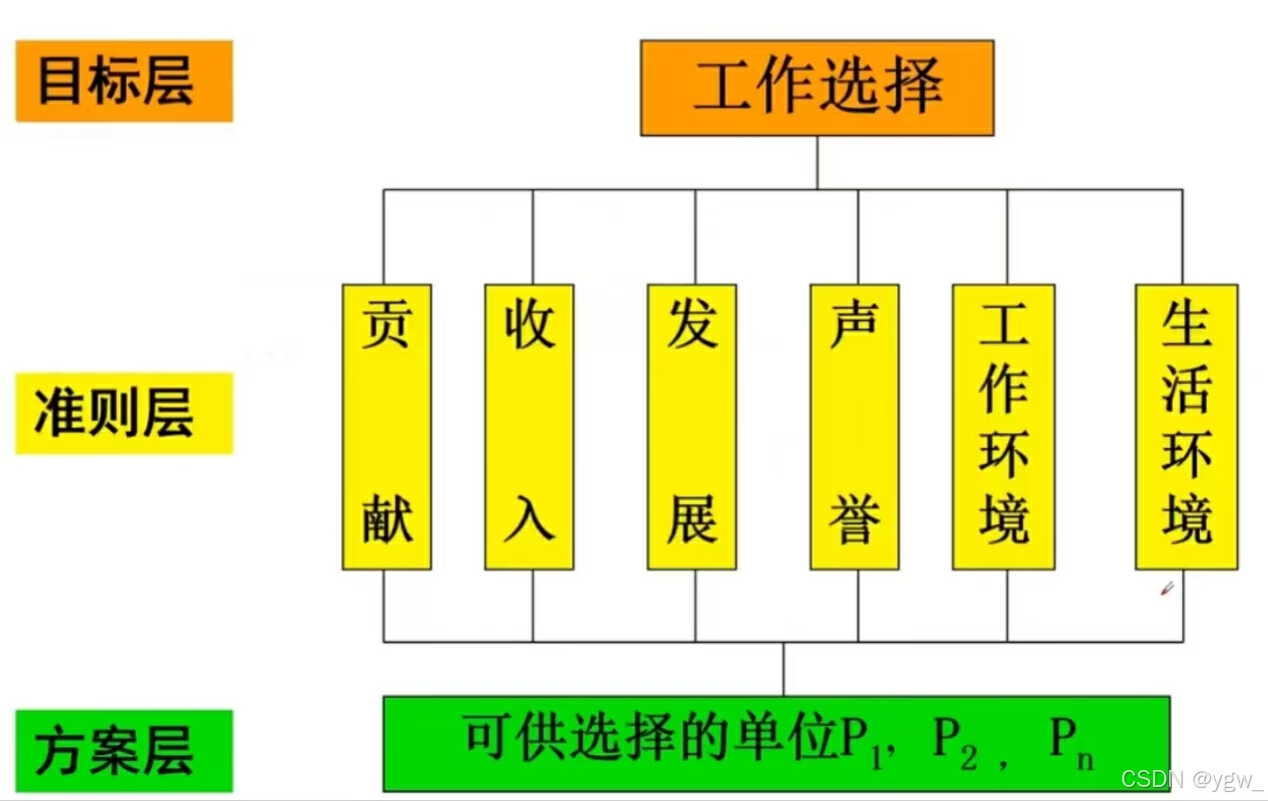
将决策的目标、考虑的因素（决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最底层，绘出层次结构图。

最高层：决策的目标、要解决的问题。

最底层：决策时的备选方案。

中间层：考虑的因素、决策的准则。

对相邻的两层，称高层为目标层，低层为因素层。

例题如下：

获得大学毕业学位的毕业生，在“双向选择”时，用人单位与毕业生都有各自的选择标准和要求。就毕业生来说选择单位的标准和要求是多方面的，例如：
①能发挥自己才干作出较好贡献（即工作岗位适合发挥自己的专长）；
②工作收入较好（待遇好）；
③生活环境好（大城市、气候等工作条件等）；
④单位名声好（声誉等）；
⑤工作环境好（人际关系和谐等）
⑥发展晋升机会多（如新单位或前景好）等。

eg：

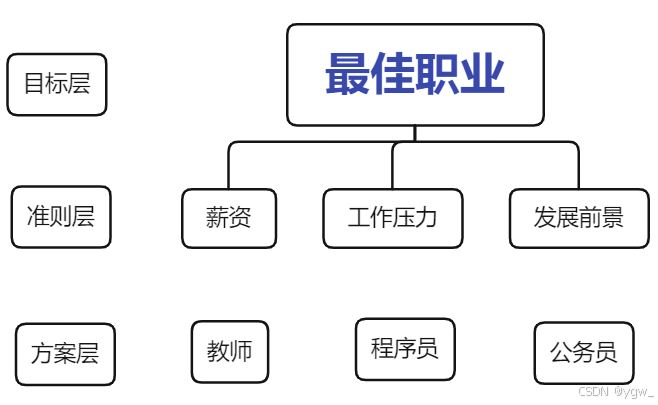
小李刚毕业，在考虑三种职业：教师、程序员、公务员，他从薪资、工作压力、发展前景这三个面来进行考虑选择职业。

从题中获去关键信息，来建立层次结构模型，很明显小李是想找到一份适合自己的工作，所以选择职业为目标层，选择什么职业的前提条件或者是影响因素为：薪资、工作压力、发展前景，也就是准则层，最后有教师、程序员、公务员这三种方案也就是方案层。

二、构造判断（成对比较）矩阵

1.不把所有因素放在一起比较，而是两两相互比较
2.对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比
较的困难，以提高准确度。
判断矩阵是表示本层所有因素针对上一层某一个因素的相对重要性的
比较。

判断矩阵的元素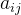 $a_{ij}$ ,用Santy的1-9标度方法给出。

我们针对上一题来说，对于每一个准则（薪资、工作压力、发展前景），都要构建一个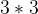 3*3 的判断矩阵。以薪资为例，判断矩阵A的元素 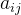$a_{ij}$ 表示相对于薪资的准则，第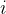种职业与第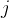种职业的相对重要性程度之比。

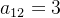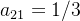我们这里假设小李相对于薪资而言，程序员比教师更重要，可以给程序员和教师相对重要性赋值。这里我们通常采用1-9标度法（看上图），我们这里认为程序员薪资比教师薪资重要程度为3，那么 $a_{12}=3$ ,那 $a_{21}=1/3$ （看上图最后一行）。同理我这里直接给出 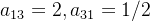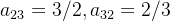$a_{13}=2,a_{31}=1/2$ , $a_{23}=3/2,a_{32}=2/3$ 这样就得到关于薪资的判断矩阵 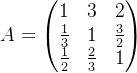$A = \begin{pmatrix} 1 & 3 & 2 \\ \frac{1}{3} & 1 & \frac{3}{2} \\ \frac{1}{2} & \frac{2}{3} & 1 \end{pmatrix}$ ，同理我们可以得到关于工作压力和的判断矩阵 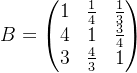$B = \begin{pmatrix} 1 & \frac{1}{4} & \frac{1}{3} \\ 4 & 1 & \frac{3}{4} \\ 3 & \frac{4}{3} & 1 \end{pmatrix}$ ，对于发展前景也构建类似的判断矩阵C ，其元素同样根据小李对三种职业在发展前景方面的相对重要性的判断来确定。

三、层次单排序及其一致性检验

层次单排序是指针对上一层某元素将本层中所有元素两两比较，并开展层次排序，进行重要顺序的排列。

对应于判断矩阵最大特征根入max的特征向量，经归一化（使向量中各元素之和等于1）后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值，这一过程称为层次单排序。
能否确认层次单排序，需要进行一致性检验，所谓一致性检验是指对A确定不一致的允许范围。

定理：n阶一致阵的唯一非零特征根为n
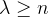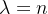定理：n阶正互反阵A的最大特征根 $\lambda \ge n$ ，当且仅当 $\lambda =n$ 时A为一致阵

定义一致性指标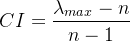： $CI = \frac{\lambda_{max}-n}{n - 1}$

CI=0，有完全的一致性

CI接近于0，有满意的一致性

CI越大，不一致越严重

为了衡量CI的大小，引入随机一致性指标RI。方法为：随机构造500个成对比较矩阵 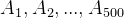$A_1,A_2,...,A_{500}$ ，则可得一致性指标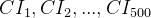 $CI_1,CI_2,...,CI_{500}$

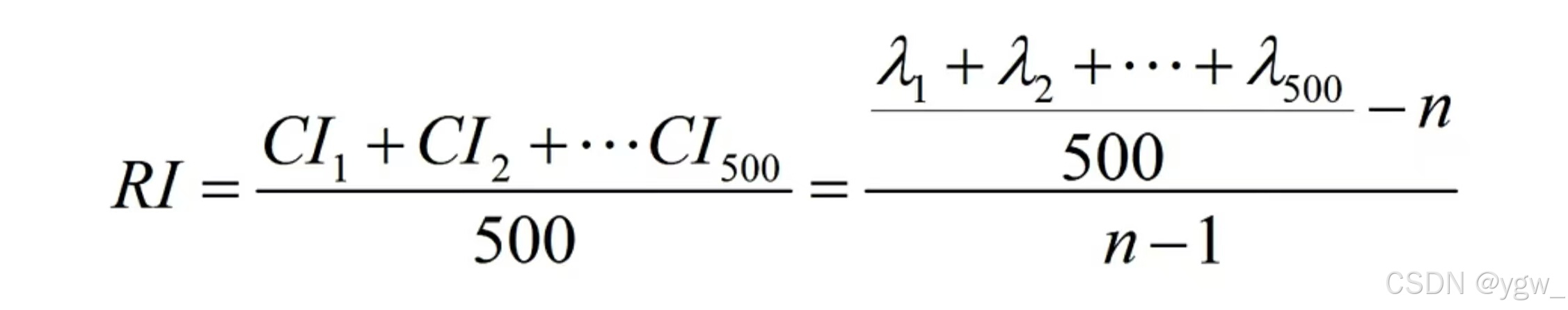
定义一致性比率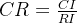： $CR = \frac{CI}{RI}$

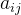当 $CR = \frac{CI}{RI}<0.1$ 时，认为A的不一致程度在容许范围之内，有满意的一致性，通过一致性检验。可用其归一化特征向量作为权向量，否则要重新构造成对比较矩阵A，对 $a_{ij}$ 加以调整。一致性检验：利用一致性指标和一致性比率<0.1及随机一致性指标的数值表，对A进行检验的过程。

eg: 对于每一个判断矩阵（薪资判断矩阵 A、工作压力判断矩阵 B、发展前景判断矩阵C ），计算其最大特征值 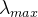$\lambda_{max}$ 对应的特征向量，这个特征向量经过归一化后就是各职业在该准则下的权重向量。我们以判断矩阵A为例，设 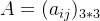$A=(a_{ij})_{3*3}$ ,求解特征方程 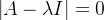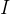$\left | A-\lambda I \right |=0$ （为单位矩阵）得到最大特征值 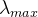$\lambda _{max}$ ,再通过求解 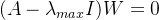$(A-\lambda _{max}I)W=0$ (W是特征向量)，得到特征向量 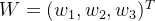W=(w_1 ,w_2,w_3)^T ,最后将W归一化，即 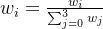$w_i=\frac{w_i}{\sum^3_{j=0}w_j }$ ,得到薪资准则下教师、程序员、公务员三种职业的权重向量 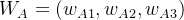$W_A=(w_{A1},w_{A2},w_{A3})$ 。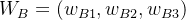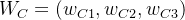同样的方法可以得到工作压力准则下的权重向量 $W_B=(w_{B1},w_{B2},w_{B3})$ 和发展前景准则下的权重向量 $W_C=(w_{C1},w_{C2},w_{C3})$ 。

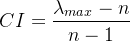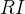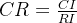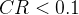计算一致性指标 $CI = \frac{\lambda_{max}-n}{n - 1}$ ，（n是矩阵阶数，这里为3）。然后查找平均随机一致性指标的值（当n=3时， RI=0.58 ），计算一致性比例 $CR=\frac{CI}{RI}$ 。如果 CR<0.1 ，则认为判断矩阵的一致性是可以接受的；否则，需要重新调整判断矩阵。对矩阵 A、B、C 都要进行这样的一致性检验。

四、层次总排序及其一致性检验

层次总排序是指从最高层（目标层）到最低层（方案层）逐层计算各元素的权重，最终得出最低层元素（方案）的总权重排序。

（1）计算各层次的权重

目标层到准则层的权重：通过准则层对目标层的判断矩阵，计算出准则层各准则的权重向量 W(1)。

准则层到方案层的权重：对于每个准则，分别计算方案层各方案相对于该准则的权重向量 Wj(2)。

（2）合成总权重

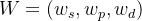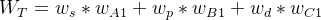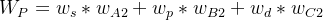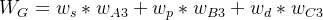设薪资、工作压力、发展前景这三个准则的权重向量为 W=(w_s,w_p,w_d) （这个权重向量可以根据小李对这三个准则的重视程度来构建一个新的判断矩阵并计算得到）。那么教师职业的总排序权重 $W_T=w_s*w_{A1}+w_p*w_{B1}+w_d*w_{C1}$ ，程序员职业的总排序权重 $W_P=w_s*w_{A2}+w_p*w_{B2}+w_d*w_{C2}$ ，公务员职业的总排序权重 $W_G=w_s*w_{A3}+w_p*w_{B3}+w_d*w_{C3}$ 。

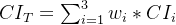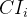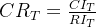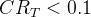计算层次总排序的一致性指标 $CI_T=\sum ^3_{i=1}w_i*CI_i$ （其中 CI_i 是每个准则对应的判断矩阵的一致性指标），查找总排序的平均随机一致性指标 RI_T （计算方法较复杂，可参考相关资料），计算总排序的一致性比例 $CR_T=\frac{CI_T}{RI_T}$ 。如果 CR_T<0.1 ，则层次总排序结果是合理的；否则，需要重新考虑判断过程。