问题描述：求第n个斐波那契数。斐波那契数列定义为：F(0)=0, F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2）。
动态规划解法：使用一个数组存储已计算的斐波那契数，避免重复计算。
/*这段代码首先检查输入的n是否小于等于1，如果是，则直接返回n，
因为斐波那契数列的前两项分别是0和1。
然后，我们创建一个dp数组来存储斐波那契数列的值，并初始化前两项。
接着，使用一个循环从第2项开始计算到第n项，每一项都是前两项的和。最后，返回第n项的值。*/
#include 问题描述
给定n个物品，每个物品有其重量w[i]和价值v[i]，以及一个背包的容量W。每个物品只有一件，可以选择放入或不放入背包中（0/1选择），求背包能够装载的最大价值。
动态规划解法：使用二维数组存储每种重量下的最大价值。
/*
初始化DP数组：创建一个二维数组dp，其中dp[i][j]表示考虑前i个物品，在不超过重量j的条件下，
背包能够装载的最大价值。
状态转移方程：对于每个物品i和每个可能的重量j，我们有两种选择：
不放入当前物品，即dp[i][j] = dp[i - 1][j]。
放入当前物品，前提是当前物品的重量不超过j，即
dp[i][j] = v[i - 1] + dp[i - 1][j - w[i - 1]]。
选择这两种情况中的最大值作为dp[i][j]的值。
返回结果：最终，dp[n][W]即为所求的最大价值，其中n是物品的数量，W是背包的容量。*/
#include 题目描述
小明每周上班都会拿到自己的工作清单，工作清单内包含n项工作，每项工作都有对应的耗时时长(单位h)和报酬，工作的总报酬为所有已完成工作的报酬之和。那么请你帮小明安排一下工作，保证小明在指定的工作时间内工作收入最大化。
输入描述 接下来是n行，每行包含两个整数t，w。t代表该项工作消耗的时长(单位h，t>0)，w代表该项工作的报酬。 输出描述
输入的第一行为两个正整数工 T，n。T 代表工作时长(单位h，0
输出小明指定工作时长内工作可获得的最大报酬。#include
最长公共子序列（Longest Common Subsequence, LCS）问题是计算机科学中的一个经典问题，它要求找出两个序列（通常是字符串）的最长公共子序列，且要求子序列中的元素在原序列中是连续的。
问题描述
给定两个序列 X 和 Y，求它们的最长公共子序列的长度。
#include class="hide-preCode-box">问题描述：给定一个整数序列 a1, a2, …, an，求其最长递增子序列的长度。
动态规划解法：使用一维数组存储到当前位置为止的最长递增子序列长度。
/*初始化DP数组：创建一个一维数组dp，其中dp[i]表示以a[i]结尾的最长递增子序列的长度。
每个元素至少是1，即自身。
状态转移方程：
对于每个元素a[i]，我们检查它之前的所有元素a[j]（其中j < i）。
如果a[i] > a[j]，则a[i]可以接在a[j]后面形成一个更长的递增子序列，
因此dp[i] = max(dp[i], dp[j] + 1)。
返回结果：最终，dp数组中的最大值即为所求的最长递增子序列的长度。*/
#include class="hide-preCode-box">问题描述：给定一系列的矩阵，求将它们相乘的最小计算量。
动态规划解法：使用三维数组存储不同矩阵组合的最小乘法次数。
/*初始化DP数组：创建一个二维数组dp，其中dp[i][j]表示将矩阵A_i到A_j相乘的最小乘法运算次数。
状态转移方程：
对于每个可能的矩阵链长度len（从2到n），我们考虑所有可能的起始矩阵i和结束矩阵j
（其中j = i + len - 1）。
对于每个可能的分割点k（其中i <= k < j），我们计算将矩阵链分成两部分A_i到A_k和
A_{k+1}到A_j的乘法运算次数，并加上A_i到A_k和A_{k+1}到A_j相乘的乘法运算次数。
选择最小的乘法运算次数作为dp[i][j]的值。
返回结果：最终，dp[1][n]即为所求的最小乘法运算次数，其中n是矩阵的数量。*/
#include class="hide-preCode-box">问题描述：给定两个字符串 str1 和 str2，求将 str1 转换为 str2 的最小编辑距离。
动态规划解法：使用二维数组存储两个字符串之间的编辑距离。
#include class="hide-preCode-box">问题描述：给定不同面额的硬币和总金额，计算组成总金额的最少硬币数量。
动态规划解法：使用一维数组存储达到每个金额所需的最少硬币数量。
/*初始化DP数组：创建一个一维数组 dp，其中 dp[i] 表示组成金额 i 的最少硬币数量。
所有值初始化为最大值 INT_MAX，表示初始状态下无法组成任何金额。
边界条件：dp[0] = 0，表示金额为0时不需要任何硬币。
状态转移方程：
对于每个金额 i（从1到 amount），我们考虑所有可能的硬币面额 coins[j]。
如果 i - coins[j] >= 0 且 dp[i - coins[j]] != INT_MAX，则表示可以使用面额为 coins[j] 的硬币，更新 dp[i] = min(dp[i], dp[i - coins[j]] + 1)。
返回结果：最终，dp[amount] 即为所求的最少硬币数量。如果 dp[amount] 仍为 INT_MAX，则表示无法组成总金额 amount，返回 -1。*/
#include class="hide-preCode-box">问题描述：在一个二维矩阵中，从左上角到右下角，只能向右或向下移动，求路径的最小和。
动态规划解法：使用二维数组存储到达每个点的最小路径和。
/*初始化DP数组：创建一个二维数组 dp，
其中 dp[i][j] 表示从左上角到位置 (i, j) 的最小路径和。
边界条件：
dp[0][0] = matrix[0][0]，表示起点的路径和就是起点的值。
对于第一行和第一列，只能从左边或上边移动过来，所以路径和是累加的。
状态转移方程：
对于其他位置 (i, j)，可以从上面 (i-1, j) 或左边 (i, j-1) 移动过来，
选择较小的路径和，并加上当前位置的值 matrix[i][j]。
返回结果：最终，dp[m-1][n-1] 即为所求的最小路径和，其中 m 和 n 分别是矩阵的行数和列数*/
#include class="hide-preCode-box">问题描述：给定股票价格序列，确定买卖股票的最佳时机以获得最大利润。
动态规划解法：使用一维数组存储每个时间点的最大利润。
/*初始化DP数组：创建一个一维数组 dp，其中 dp[i] 表示前 i 天的最大利润。
所有值初始化为0，表示初始状态下没有利润。
状态转移方程：
对于每一天 i（从1到 n-1），我们比较第 i 天的股票价格和第 i-1 天的股票价格。
如果 prices[i] > prices[i - 1]，则表示今天可以卖出股票获得利润，
更新 dp[i] = dp[i - 1] + (prices[i] - prices[i - 1])。
如果 prices[i] <= prices[i - 1]，则表示今天卖出股票不会获得利润，
保持 dp[i] = dp[i - 1]。
返回结果：最终，dp[n-1] 即为所求的最大利润，其中 n 是股票价格序列的长度。*/
#include class="hide-preCode-box">10.三步问题
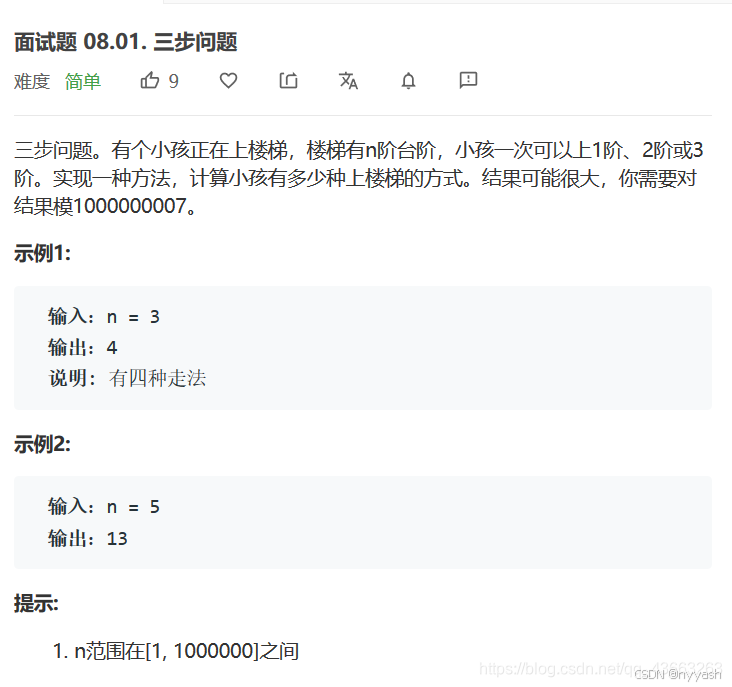
class Solution {
public:
int waysToStep(int n) {
long long dp[1000000]={0};
dp[1]=1;
dp[2]=2;
dp[3]=4;
for(int i=4;i<=n;i++)
{
dp[i]=(dp[i-1]+dp[i-2]+dp[i-3])%1000000007;
}
return dp[n];
}
};
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
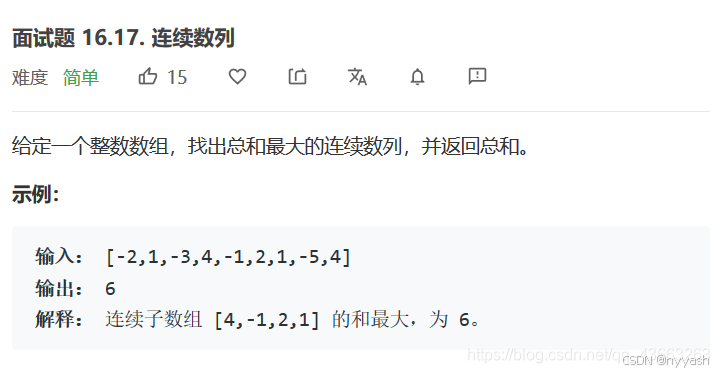
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int dp[100000]={0};
int ans=nums[0];
dp[0]=nums[0];
for(int i=1;i<nums.size();i++)
{
dp[i]=max(nums[i],dp[i-1]+nums[i]);
ans=max(dp[i],ans);
}
return ans;
}
};
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}">
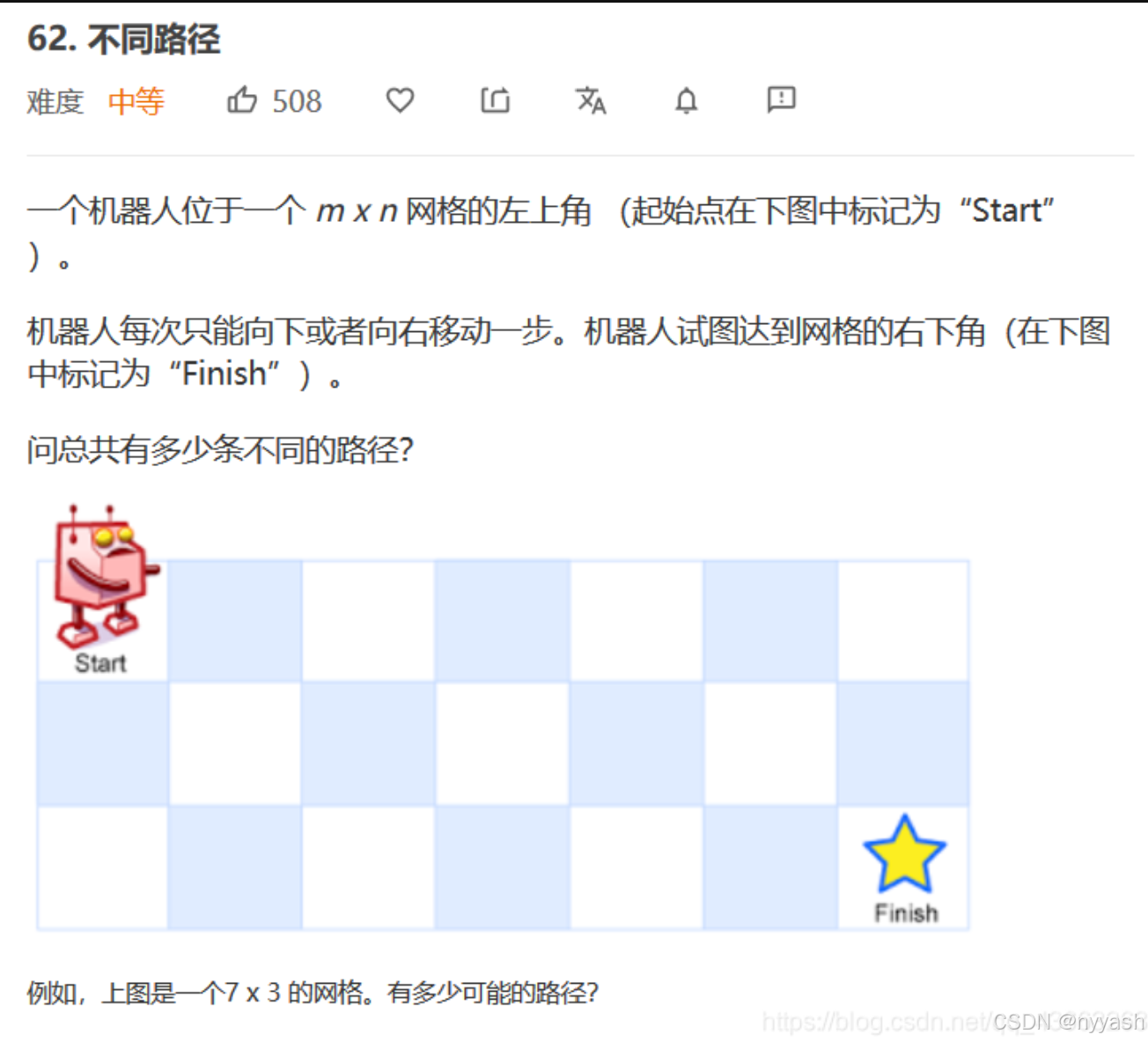
class Solution {
public:
int uniquePaths(int m, int n) {
int dp[m][n];
if(m==0||n==0)
return 0;
for(int i=0;i<n;i++)
{
dp[0][i]=1;
}
for(int i=0;i<m;i++)
{
dp[i][0]=1;
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}"> class="hide-preCode-box">
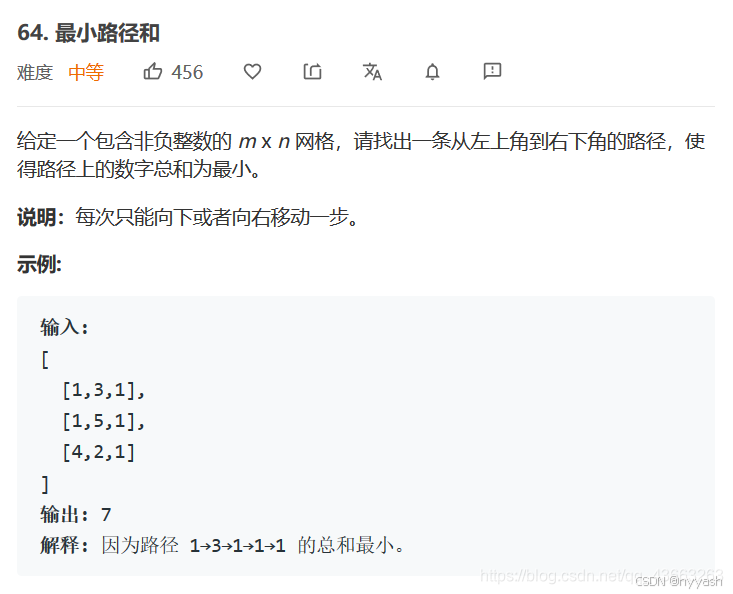
这题和上题很类似，转移方程也十分的相似，因为只能向右或者向下走，所以我们只要考虑向下和向右走哪个能符合题目条件即可，我们可以将上题的转移方程变式一下，就可以得到：
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int dp[grid.size()][grid[0].size()];
dp[0][0]=grid[0][0];
for(int i=1;i<grid.size();i++)
dp[i][0]=dp[i-1][0]+grid[i][0];
for(int i=1;i<grid[0].size();i++)
dp[0][i]=dp[0][i-1]+grid[0][i];
for(int i=1;i<grid.size();i++)
{
for(int j=1;j<grid[0].size();j++)
{
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[grid.size()-1][grid[0].size()-1];
}
};
class="hljs-button signin active" data-title="登录复制" data-report-click="{"spm":"1001.2101.3001.4334"}"> class="hide-preCode-box">
评论记录：
回复评论：