目录
题目二——416. 分割等和子集 - 力扣(LeetCode)
题目四——1049. 最后一块石头的重量 II - 力扣(LeetCode)
题目二—— 322. 零钱兑换 - 力扣(LeetCode)
题目三——518. 零钱兑换 II - 力扣(LeetCode)
题目四——279. 完全平方数 - 力扣(LeetCode)
题目一——377. 组合总和 Ⅳ - 力扣(LeetCode)
背包问题
背包问题其实是你有一个背包,然后地上有一堆物品,然后你去挑选一些物品放到背包之中,然后问你最大能挑选出来的价值是多少?
但是实际的情况没有这么简单,我们需要考虑背包的属性和物品的属性。这样子难度就上来了。
换句话说背包问题简单来说就是选与不选的问题,其本质就是一种有限制条件的组合问题。
给你一个“背包”,这个“背包”的体积是V,给你一堆“物品”,这些“物品”每一个都有价值w和体积v,让你选择一些放入“背包”,得到最大(最小)价值。
背包问题是一个顺序无关的问题,即与我们选的“物品”顺序无关。顺序无关是组合问题的一个特点。比如我们选物品a,b,c,跟选c,b,a是没有区别的。
那顺序有关是什么?那就是排列问题了。排列问题我们选物品a,b,c,跟选c,b,a是有区别的。
背包问题是一种DP模型,往往题目不会直接告诉你:给你一个背包,让你选物品巴拉巴拉。而是将这个问题转化成别的,这就是为什么我上面的背包和物品会加引号。具体怎么回事大家可看后面的例题。
我们要理解背包问题的本质,其本质就是一个组合问题。题目让我们求的往往是这个组合子集的数量,或者说用这个组合能得到的最大价值(至多型)、最小价值(至少型)。
背包问题其实是动态规划的核心,但是由于背包问题的种类繁多,而且背包问题的难度层次不齐,有的题目已经升级到竞赛难度了,所以我们这里只讲01背包问题和完全背包问题。
那什么是01背包问题和完全背包问题呢?
- 01背包问题:简单来说01背包是给你一个体积为V的背包,给你一堆物品,每个物品的价值是w,每件物品至多选一个(每个物品就能选一次,也可以不选)。
- 完全背包问题:简单来说完全背包是给你一个体积为V的背包,给你一堆物品,每个物品的价值是w,每件物品可以选无数个,不只是1个,爱选几个选几个。
其中01背包是所有背包的问题是所有问题的基础,我们需要好好的学习01背包
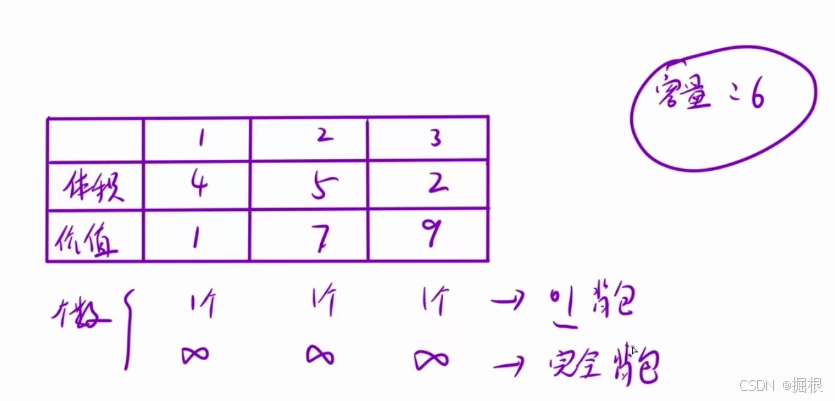
这里根据放入背包的物品的总体积可以分出三类
- 必须装满:一个是放入背包的物品的总体积恰好是V
- 不必装满:一种是放入背包的物品的总体积至多是V(也可以不是V)
光是上面四种情况的组合就有很多种情况了,那就说明了我们的背包问题有特别多的。
好,我们就先讲那么多,后面需要的情况下再慢慢补充
一. 01背包问题
题目一——【模板】01背包_牛客题霸_牛客网
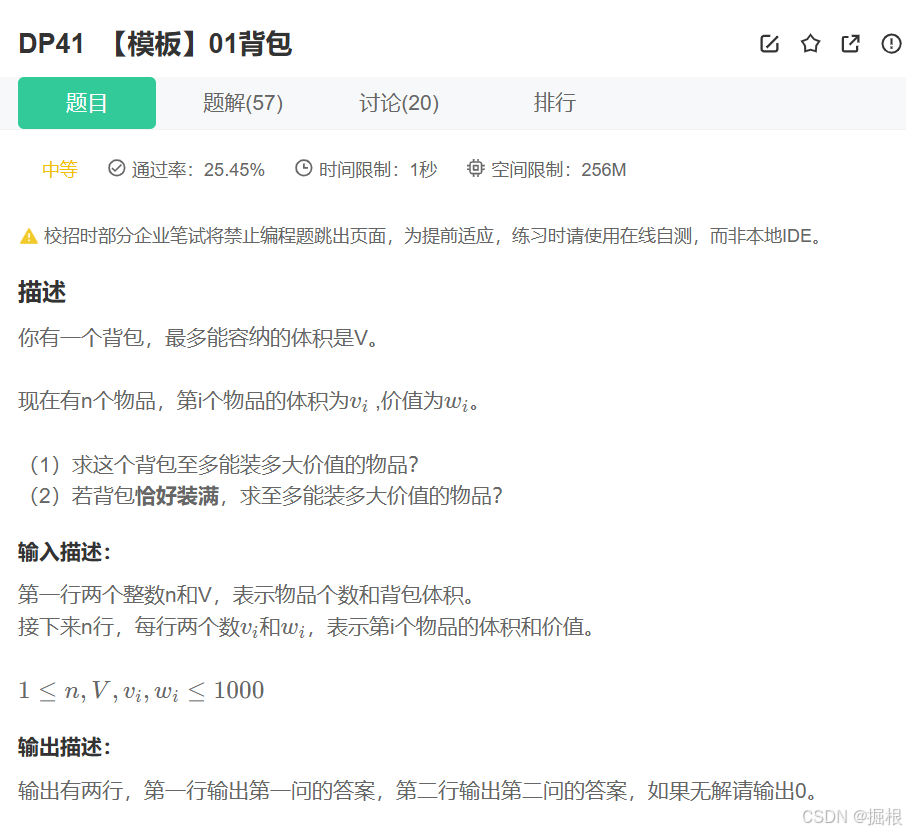


我们看看一个例子:
输入:
- 3 5
- 2 10
- 4 5
- 1 4
第一个3代表一共有3种物品可供选择。
物品信息:
- 物品1:体积2,价值10
- 物品2:体积4,价值5
- 物品3:体积1,价值4
背包容量:5
分析:
- 第一问:背包至多能装多大价值的物品?
- 如果选择物品1和物品3,总体积为2+1=3,总价值为10+4=14,这是最大价值。
- 因此,第一问的答案是14。
- 第二问:若背包恰好装满,求至多能装多大价值的物品?
- 如果选择物品2和物品3,总体积为4+1=5,总价值为5+4=9,这是恰好装满背包的最大价值。
- 因此,第二问的答案是9。
输出:
- 14
- 9
假设物品个数为N,那么我们需要搞两个数组:
- 大小为N+1的v[N+1]:其中v[0]是不存储有效信息的结点,v[i]代表第i件物品的体积
- 大小为N+1的w[N+1]:其中w[0]是不存储有效信息的结点,w[i]代表第i件物品的体积
我们先解决第一个问题:第一问:背包至多能装多大价值的物品?说白了就是要找最大值。
1.状态表示
首先我们为了保证dp[1][j]是代表从第一个物品里面挑选,我们将dp表多开一行一列。
dp[i][j] 表示:从前 i 个物品中挑选,总体积「不超过」j,所有的选法中,能挑选出来的最大价值。
2.状态转移方程:
线性 dp 状态转移方程分析方式,一般都是根据「最后一步」的状况,来分情况讨论:
- 不选第 i 个物品:相当于就是去前 i-1 个物品中挑选,并且总体积不超过 j。此时 dp[i][j] = dp[i - 1][j] ;
- 选择第 i 个物品:那么我就只能去前 i-1 个物品中,挑选总体积不超过 j-v[i] 的物品。此时 dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不一定存在(比如说j
综上,状态转移方程为:
- dp[i][j] = dp[i - 1][j];
- if(j>=v[i])
- {
- dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
- }
3.初始化:
我们多加一行,方便我们的初始化,此时仅需将第一行初始化为满足体积不小于 j 的情况,此时的价值为 0。
4.填表顺序:
根据「状态转移方程」,我们仅需「从上往下」填0 即可。因为什么也不选,也是一种合法的选法。
5.返回值:
根据「状态表示」,返回 dp[n][V] 。
这样子,我们第一题的代码已经可以写出来了。
- #include
- using namespace std;
-
- int main() {
- int n,V;
- cin>>n>>V;
-
- vector<int>v(n+1);
- vector<int>w(n+1);
- for(int i=1;i<=n;i++)
- {
- cin>>v[i]>>w[i];
- }
-
- vector
int>>dp(n+1,vector<int>(V+1,0)); - for(int i=1;i<=n;i++)
- {
- for(int j=0;j<=V;j++)
- {
- dp[i][j] = dp[i - 1][j];
- if(j>=v[i])
- {
- dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
- }
- }
- }
- cout << dp[n][V] << endl;
- }
我们接着解决第2问!!
1.状态表示
dp[i][j] 表示:从前 i 个物品中挑选,总体积等于j,所有的选法中,能挑选出来的最大价值。
2.状态转移方程:
线性 dp 状态转移方程分析方式,一般都是根据「最后一步」的状况,来分情况讨论:
- 不选第 i 个物品:相当于就是去前 i-1 个物品中挑选,并且总体积等于j。此时 dp[i][j] = dp[i - 1][j] ;
- 选择第 i 个物品:那么我就只能去前 i-1 个物品中,挑选总体积等于 j-v[i] 的物品。此时 dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不一定存在,因此需要特判一下。
注意这题可和上面不一样啊,恰好装满是一个非常重要的关键词。比如说dp[i - 1][j - v[i]],如果说我在前i-1种物品里面选择,怎么选择都凑不到总体积是j - v[i],那我怎么办?dp[i - 1][j - v[i]]填什么?对于这种情况我们设置了-1代表该情况不存在的意思
综上,状态转移方程为:
- dp[i][j] = dp[i - 1][j];
- if(j>=v[i]&&dp[i-1][j-v[i]]!=-1)
- {
- dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
- }
3.初始化:
注意这题可和上面不一样啊,恰好装满是一个非常重要的关键词。比如说dp[i - 1][j - v[i]],如果说我在前i-1种物品里面选择,怎么选择都凑不到总体积是j - v[i],那我怎么办?dp[i - 1][j - v[i]]填什么?对于这种情况我们设置了-1代表该情况不存在的意思
我们要注意这个题目条件:1≤n,V,vi,wi≤1000
为了保证dp[i][j]是代表在前i件物品,总体积为j的最大价值,我们通常会多加一行一列。实际上,我们只需要初始化第一行和第一列即可。
- 第一行(i=0):表示没有物品可以选择时的情况。这种情况根本就不可能发生,因为1≤n≤1000 ,此时,对于所有 j(背包容量),dp[0][j] 都应该初始化为 -1,因为没有物品可以选择。
- 第一列(j=0):表示背包容量为 0 时的情况。这种情况根本就不可能发生,因为1≤n≤1000 ,此时,对于所有 i(物品数量),dp[i][0] 也都应该初始化为 -1,因为背包容量为 0 时,无法放入任何物品。
除了这些,其他部分都应该设置为-1。代表没有物品,⽆法满⾜体积⼤于 0 的情况。
4.填表顺序:
根据「状态转移方程」,我们仅需「从上往下」填表0 即可。因为什么也不选,也是一种合法的选法。
5.返回值:
由于最后可能凑不成体积为 V 的情况,因此返回之前需要「特判」⼀下。
- #include
- using namespace std;
-
- int main() {
- int n,V;
- cin>>n>>V;
-
- vector<int>v(n+1);
- vector<int>w(n+1);
- for(int i=1;i<=n;i++)
- {
- cin>>v[i]>>w[i];
- }
-
- vector
int>>dp(n+1,vector<int>(V+1,0)); - for(int i=1;i<=n;i++)
- {
- for(int j=0;j<=V;j++)
- {
- dp[i][j] = dp[i - 1][j];
- if(j>=v[i])
- {
- dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
- }
- }
- }
- cout << dp[n][V] << endl;
-
- vector
int>>dp2(n+1,vector<int>(V+1,0)); - for(int i=1;i<=V;i++)
- dp2[0][i]=-1;
- for(int i=1;i<=n;i++)
- dp2[n][0]=-1;
-
- for(int i=1;i<=n;i++)
- {
- for(int j=0;j<=V;j++)
- {
- dp2[i][j]=dp2[i-1][j];
- if(j>=v[i]&&dp2[i-1][j-v[i]]!=-1)
- {
- dp2[i][j]=max(dp2[i-1][j],dp2[i-1][j-v[i]]+w[i]);
- }
- }
- }
- if(dp2[n][V]==-1)
- {
- cout<<0<
- }
- else
- {
- cout<
- }
- }
实际上,在竞赛里面,我们通常将数组开辟成全局变量
全局数组版本
- #include
- #include
- using namespace std;
- const int N = 1010;
- int n, V, v[N], w[N];
- int dp[N][N];
- int main() {
- // 读⼊数据
-
- cin >> n >> V;
- for (int i = 1; i <= n; i++)
- cin >> v[i] >> w[i];
- // 解决第⼀问
-
- for (int i = 1; i <= n; i++)
- for (int j = 0; j <= V; j++) // 修改遍历顺序
-
- {
- dp[i][j] = dp[i - 1][j];
- if (j >= v[i])
- dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
- }
-
- cout << dp[n][V] << endl;
- // 解决第⼆问
-
- memset(dp, 0, sizeof dp);
- for (int j = 1; j <= V; j++) dp[0][j] = -1;
- for (int i = 1; i <= n; i++)
- for (int j = 0; j <= V; j++) // 修改遍历顺序
-
- {
- dp[i][j] = dp[i - 1][j];
- if (j >= v[i] && dp[i - 1][j - v[i]] != -1)
- dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
- }
-
- cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;
- return 0;
- }
6.优化点
我们知道这个状态转移方程里面dp[i][j]只依赖了dp[i-1][j]和dp[i-1][j-v[i]]两个位置的值。
也就说说第i行的数据是完完全全依赖于第i-1行的数据的
那是不是说明我们只需要第i行和第i-1行,其他的都不要
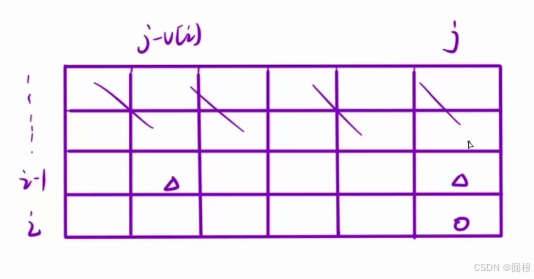
像这样子,只依赖于上一行的值的情况,我们就可以使用滚动数组来优化。
那意味着我们是不是只需要搞两个数组,就能完成这个dp
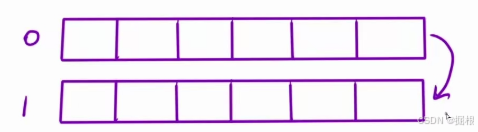
填完之后我们将第0行存放第2行的值。
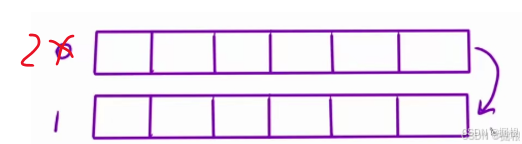
然后填第3行的时候,将数值填到原来存放第一行数值的那个数组里面即可。
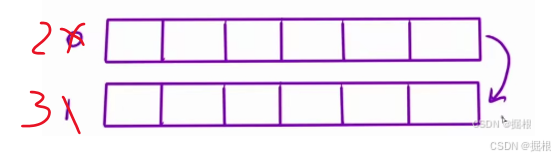
就这样子一直滚动下去即可。
但是利用两个数组,我还是感觉有点浪费了。我们能不能使用一个数组来存储这个信息?
答案是可以的。
使用一个数组的思想和两个数组的一模一样。
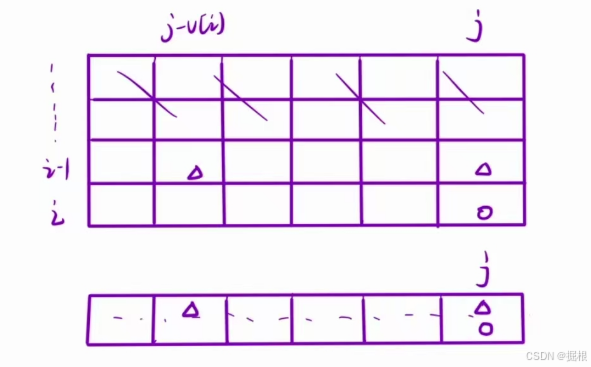
虚线代表上一行的意思。
也就是说,我们直接忽略了行数的存在。只用一行完成我所有的dp
首先,这个一维数组存的是原本二维dp表第0行的数据。
现在要存原本二维dp表第1行的数据的话,有两种选择
- 从左边往右边填
- 从右边往左边填
但是我告诉你从左边往右边填是不行的。因为原来dp[i][j]只依赖了dp[i-1][j]和dp[i-1][j-v[i]]两个位置的值,现在一维数组的情况下,dp[j]只依赖了原来的dp[j]和原来的dp[j-v[i]]两个位置的值。如果我从左往右边遍历,那我原来的dp[j-v[i]]就会在使用之前先被修改,这样子我就不能填出dp[j]了。
所以我们选择从右边往左边填。
我们很快就能写出下面这个代码
- #include
- using namespace std;
-
- // 定义常量N,表示物品的最大数量(同时也是背包容量数组dp的大小)
- const int N = 1010;
-
- // 定义全局变量
- int n, V; // n表示物品数量,V表示背包容量
- int v[N], w[N]; // v[i]表示第i个物品的重量,w[i]表示第i个物品的价值
- int dp[N]; // dp[j]表示容量为j的背包能装下的最大价值
-
- int main() {
- //读⼊数据
- cin >> n >> V;
- for (int i = 1; i <= n; i++)
- cin >> v[i] >> w[i];
-
- //解决第⼀问
- for (int i = 1; i <= n; i++)
- for (int j = V; j >= v[i]; j--) //修改遍历顺序
- dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
-
- cout << dp[V] << endl;
-
- //解决第⼆问
- memset(dp, 0, sizeof dp);
- for (int j = 1; j <= V; j++) dp[j] = -1;
- for (int i = 1; i <= n; i++)
- for (int j = V; j >= v[i]; j--)
- if (dp[j - v[i]] != -1)
- dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
-
- cout << (dp[V] == -1 ? 0 : dp[V]) << endl;
-
- return 0;
- }
背包问题基本上都是利⽤「滚动数组」来做空间上的优化:
- 利⽤「滚动数组」优化;
- 直接在「原始代码」上修改。
在01背包问题中,优化的结果为:
- 删掉所有的横坐标;
- 修改⼀下 j 的遍历顺序。
题目二——416. 分割等和子集 - 力扣(LeetCode)


首先,我们需要将这个问题转化为我们“熟悉”的题型。
如果数组能够被分成两个子集,使得这两个子集内相同元素之和相同,那么原数组必须满足以下性质:
- 所有元素之和应该是一个偶数;
- 数组中的最大元素应该小于所有元素总和的一半;
- 存在一种选择方式,使得选出的元素总和等于数组总和的一半。
根据前两个性质,我们可以提前判断数组是否可能被划分。而根据最后一个性质,我们发现问题实际上转化为了一个“01背包”问题:
- 数组中的元素相当于背包问题中的物品,每个物品只能选择一次;
- 每个元素面临被选择或不被选择的两种可能;
- 需要选出一些元素,使它们的总和等于数组总和的一半。
接下来,我们用背包问题的分析方式来处理这道题。
状态表示:
设dp[i][j]表示在前i个元素中选择,是否存在一种选法使得总和为j。
状态转移方程:
根据“最后一个位置”的元素,我们分情况讨论:
- 不选择
nums[i]:此时能否凑成总和为j,取决于前i-1个元素中能否凑成总和为j。即dp[i][j] = dp[i-1][j]。 - 选择
nums[i]:这种情况下有一个前提条件,即nums[i]应小于等于j(否则选择它就没有意义)。此时能否凑成总和为j,取决于前i-1个元素中能否凑成总和为j-nums[i]。即如果nums[i] <= j,则dp[i][j] = dp[i-1][j-nums[i]](或dp[i][j] = dp[i][j] || dp[i-1][j-nums[i]],以考虑之前的状态)。
综合以上两种情况,状态转移方程为:
- dp[i][j] = dp[i-1][j];
- if(nums[i-1] <= j)
- dp[i][j] = dp[i][j] || dp[i-1][j-nums[i]];
初始化:
由于需要用到上一行的数据,我们可以先初始化第一行。第一行表示不选择任何元素时的情况,只有当目标和为0时才能凑成,因此dp[0][0] = true,其他均为false。
填表顺序:
根据状态转移方程,我们需要从上往下填写每一行,每一行内部的顺序则无关紧要。
返回值:
根据状态表示,返回dp[n][aim]的值,其中n表示数组的大小,aim表示要凑的目标和。
- class Solution {
- public:
- bool canPartition(vector<int>& nums) {
- int n = nums.size(), sum = 0;
- for (auto x : nums)
- sum += x;
- if (sum % 2 == 1)
- return false; // 如果不能平分,直接返回
-
- int aim=sum/2;
- vector
bool>>dp(n+1,vector<bool>(aim+1,false)); - for(int i = 0; i <= n; i++) dp[i][0] = true; // 初始化
-
- for(int i=1;i<=n;i++)
- {
- for(int j=1;j<=aim;j++)
- {
- dp[i][j]=dp[i-1][j];
- if(j>=nums[i-1])
- {
- dp[i][j]=dp[i][j]||dp[i-1][j-nums[i-1]];
- }
- }
- }
- return dp[n][aim];
- }
- };
 空间优化:
空间优化:
对于01背包问题,我们可以进行空间优化。优化策略是删掉第一维,并修改第二层循环的遍历顺序(从后往前遍历,以避免重复使用同一物品)。
- class Solution {
- public:
- bool canPartition(vector<int>& nums) {
- int n = nums.size(), sum = 0;
- for (auto x : nums)
- sum += x;
- if (sum % 2 == 1)
- return false; // 如果不能平分,直接返回
-
- int aim=sum/2;
- vector<bool>dp(aim+1,false);
- dp[0] = true; // 初始化
-
- for(int i=1;i<=n;i++)
- {
- for(int j=aim;j>=1;j--)
- {
- if(j>=nums[i-1])
- {
- dp[j] = dp[j] || dp[j - nums[i - 1]];
- }
- }
- }
- return dp[aim];
- }
- };
题目三——494. 目标和 - 力扣(LeetCode)


如果说我们直接使用动态规划来做这题的话是有点小困难的,所以我们不能直接做。我们得先将其转换一下
注意:
0 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000
设我们最终选取的结果中,前面加+号的数字之和为 a,前⾯加-号的数字之和为b,两者的总和为 sum,于是我们有以下两个等式:
a + b = sum:表示前面加+号的数字之和 a 与前面加-号的数字之和 b 的总和等于整个被选中数字的总和 sum。a - b = target:表示前面加+号的数字之和 a 减去前面加-号的数字之和 b 等于给定的目标和 target。
这里,a 代表前面加+号的数字之和,b 代表前面加-号的数字之和,而整个数组中的数字被分为两部分,一部分前面加+,另一部分前面加-。
通过上面两个等式,我们可以消去 b,得到:
a = (sum + target) / 2
也就是说,我们仅需在 nums 数组中选择一些数(可以为正选也可以为负选,但在这里我们将其转化为只考虑正选的情况,即只考虑选择哪些数字加入到 a 中,而 b 则是由未被选中的数字构成的“负和”),将它们凑成和为 (sum + target) / 2 即可。这样,如果我们能够找到一种方案,使得选出的数字之和等于 (sum + target) / 2,那么就可以通过调整正负号来满足原问题中的 a - b = target 条件。
我们可以将这个问题视为一个背包问题,即在一个容量为 (总和 + target) / 2 的背包中,选择一些物品(数组中的数字),使得背包中的物品总重量恰好等于背包的容量。
状态表示:
dp[j] 表示从前 i 个数中选,总和正好等于 j 的方案数。
状态转移方程:
根据“最后一个位置”的元素,我们分情况讨论:
- 不选择
nums[i]:此时能否凑成总和为j,取决于前i-1个元素中能否凑成总和为j。即dp[i][j] = dp[i-1][j]。 - 选择
nums[i]:这种情况下有一个前提条件,即nums[i-1]应小于等于j(否则选择它就没有意义)。此时能否凑成总和为j,取决于前i-1个元素中能否凑成总和为j-nums[i]。即如果nums[i-1] <= j,则dp[i][j] += dp[i-1][j-nums[i-1]]。
综合以上两种情况,状态转移方程为:
- dp[i][j] = dp[i-1][j];
- if(nums[i-1] <= j)
- dp[i][j] += dp[i-1][j-nums[i]];
初始化:
其实我们要初始化第一行,但是第一行代表不选择任何一个数,只有目标和为0才能做到,所以
dp[0][0] = 1;
填表顺序:
从上往下,从左往右即可
返回值:
返回dp[n][aim]
- class Solution {
- public:
- int findTargetSumWays(vector<int>& nums, int target) {
- int sum = 0;
- for (auto x : nums)
- sum += x;
- int aim = (sum + target) / 2;
- // 处理⼀下边界条件
- if (aim < 0 || (sum + target) % 2)
- return 0;
-
- int n = nums.size();
- vector
int>> dp(n + 1, vector<int>(aim + 1, 0)); - dp[0][0] = 1; // 初始化
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= aim; j++) {
- dp[i][j] = dp[i - 1][j];
- if (j >= nums[i - 1])
- dp[i][j]+=dp[i-1][j-nums[i-1]];
- }
- }
- return dp[n][aim];
- }
- };
优化版本
这个优化策略和之前的一模一样的
- class Solution {
- public:
- int findTargetSumWays(vector<int>& nums, int target) {
- int sum = 0;
- for (auto x : nums)
- sum += x;
- int aim = (sum + target) / 2;
- // 处理⼀下边界条件
- if (aim < 0 || (sum + target) % 2)
- return 0;
-
- int n = nums.size();
- vector<int>dp(aim + 1, 0);
- dp[0] = 1; // 初始化
- for (int i = 1; i <= n; i++) {
- for (int j = aim; j >=0 ; j--) {
- if(j>=nums[i-1])
- dp[j]+=dp[j-nums[i-1]];
- }
- }
- return dp[aim];
- }
- };
题目四——1049. 最后一块石头的重量 II - 力扣(LeetCode)


其实我们仔细分析一下题目,就会发现

最后一块小石头的重量就是在原有数组各元素的基础上进行添加正号或者负号,这tm不就和我们上一道题目一模一样啊!!!
所以我们的思路和上面是一模一样的的。
问题可以转化为一个我们熟悉的题型:
- 任意两块石头在一起粉碎,重量相同的部分会被丢掉,重量有差异的部分会被留下来。这相当于在原始的数据前面,加上“加号”或者“减号”,使最终的结果最小。也就是说,把原始的石头分成两部分,两部分的和越接近越好。
- 又因为当所有元素的和固定时,分成的两部分越接近数组“总和的一半”,两者的差越小。因此,问题就变成了:在数组中选择一些数,让这些数的和尽量接近总和的一半。我们可以把每个数的值看成体积和价值,问题就变成了“01背包问题”。
接下来,我们按照“01背包问题”的思路来解题:
-
状态表示:
设总和的一半为sum / 2,如果把数看成物品,dp[i][j]表示在前i个元素中选择,总和不超过j,此时所有元素的最大和。
-
状态转移方程:
根据题目要求,我们分情况讨论:
- 不选
stones[i]:那么我们是否能够凑成总和为j,就要看在前i-1个元素中选,能否凑成总和为j。此时,dp[i][j] = dp[i-1][j]。 - 选择
stones[i]:这种情况下是有前提条件的,此时的stones[i]应该小于等于j。因为如果这个元素都比要凑成的总和大,选择它就没有意义。那么我们是否能够凑成总和为j,就要看在前i-1个元素中选,能否凑成总和为j - stones[i]。此时,dp[i][j] = dp[i-1][j - stones[i]] + stones[i]。
综上所述,我们要的是最大价值。因此,状态转移方程为:
dp[i][j] = dp[i-1][j] // 不选 stones[i]if (j >= stones[i]) dp[i][j] = max(dp[i][j], dp[i-1][j - stones[i]] + stones[i]) // 选 stones[i]
-
初始化:
由于需要用到上一行的数据,因此我们可以先把第一行初始化。第一行表示“没有石子”,因此想凑成目标和j的最大和都是0。
-
填表顺序:
根据状态转移方程,我们需要从上往下填写每一行,每一行的顺序是无所谓的。
-
返回值:
- 根据状态表示,先找到最接近
sum / 2的最大和dp[n][sum / 2]。 - 因为我们要的是两堆石子的差,因此返回
sum - 2 * dp[n][sum / 2]。
- class Solution {
- public:
- int lastStoneWeightII(vector<int>& stones) {
- int sum = 0;
- for (auto& a : stones) {
- sum += a;
- }
- int target = sum / 2;
- int n = stones.size();
- vector
int>> dp(n + 1, vector<int>(target + 1, 0)); - for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= target; j++) {
- dp[i][j] = dp[i - 1][j];
- if (j >= stones[i - 1])
- dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - stones[i - 1]]+stones[i-1]);
- }
- }
- return sum - 2 * dp[n][target];
- }
- };

6. 空间优化:
所有的背包问题,都可以进⾏「空间」上的优化。 对于01背包类型的,我们的优化策略是:
- i. 删掉第⼀维;
- ii. 修改第⼆层循环的「遍历顺序」即可。
- class Solution {
- public:
- int lastStoneWeightII(vector<int>& stones) {
- int sum = 0;
- for (auto& a : stones) {
- sum += a;
- }
- int target = sum / 2;
- int n = stones.size();
- vector<int> dp(target + 1, 0);
- for (int i = 1; i <= n; i++) {
- for (int j = target; j >= 0; j--) {
- if (j >= stones[i - 1])
- dp[j] = max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);
- }
- }
- return sum - 2 * dp[target];
- }
- };
二 . 完全背包问题
题目一——【模板】完全背包_牛客题霸_牛客网
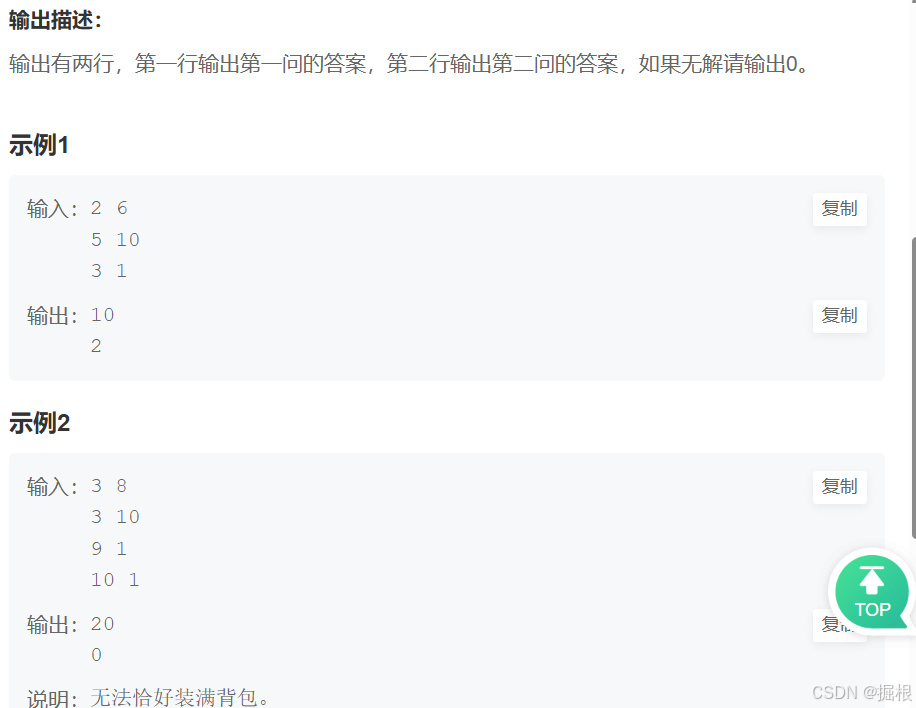

背包问题的状态表示非常经典,如果大家不知道怎么来的,就把它当成一个模板记住吧~
我们先解决第一问:(1)求这个背包至多能装多大价值的物品?
状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积不超过 j,所有的选法中,能挑选出来的最大价值。(这里和01背包有些类似,但不同的是每种物品可以挑选多次)
状态转移方程:
线性 dp 状态转移方程的分析方式,一般都是根据最后一步的状况,来分情况讨论。但是最后一个物品能选很多个,因此我们需要分很多情况来考虑:
- 选0个第
i 个物品:此时相当于就是从前 i-1 个物品中挑选,总体积不超过 j。此时最大价值为 dp[i - 1][j]。 - 选1个第
i 个物品:此时相当于就是从前 i-1 个物品中挑选,总体积不超过 j-v[i],然后再加上一个第 i 个物品的价值 w[i]。此时最大价值为 dp[i - 1][j - v[i]] + w[i]。 - 选2个第
i 个物品:此时相当于就是从前 i-1 个物品中挑选,总体积不超过 j-2*v[i],然后再加上两个第 i 个物品的价值 2*w[i]。此时最大价值为 dp[i - 1][j - 2*v[i]] + 2*w[i]。 - ...(以此类推)
综上,我们的状态转移方程为:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]]+w[i], dp[i-1][j-2*v[i]]+2*w[i], ...)
但是,我们发现计算一个状态的时候,需要一个循环才能搞定,这很不高效。优化的方向就是用一个或者两个状态来表示这一堆的状态,通常就是用数学的方式做一下等价替换。
我们发现第二维 j 是有规律的变化的,因此我们去看看 dp[i][j - v[i]] 这个状态:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]]+w[i], dp[i-1][j-2*v[i]]+2*w[i], ...)dp[i][j-v[i]] = max(dp[i-1][j-v[i]], dp[i-1][j-2*v[i]]+w[i], dp[i-1][j-3*v[i]]+2*w[i], ...)
我们发现,dp[i][j-v[i]] 加上一个 w[i] 正好和 dp[i][j] 中除了第一项以外的全部项一致,因此我们可以修改我们的状态转移方程为:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])
初始化:
我们多加一行,方便我们的初始化,此时仅需将第一行初始化为0即可。因为什么也不选,也能满足体积不小于 j 的情况,此时的价值为0。
填表顺序:
根据状态转移方程,我们仅需从上往下、从左往右填表即可(注意,由于 dp[i][j] 依赖于 dp[i][j-v[i]],因此内层循环需要按照体积 j 从小到大的顺序进行)。
返回值:
根据状态表示,返回 dp[n][V]。
- #include
- using namespace std;
-
- int main() {
- int n, V;
- cin >> n >> V;
- vector<int>v(n + 1);
- vector<int>w(n + 1);
- for (int i = 1; i <= n; i++) {
- cin >> v[i] >> w[i];
- }
- //解决第一问
- vector
int>>dp(n + 1, vector<int>(V + 1)); -
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= V; j++) {
- dp[i][j] = dp[i - 1][j];
- if (j >= w[i]) {
- dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
- }
- }
- }
- cout << dp[n][V] << endl;
- }
接着我们来完成第2问:(2)若背包恰好装满,求至多能装多大价值的物品?
其实也很简单,第二问仅需微调一下dp过程的五步即可。
因为有可能凑不齐体积为j的物品,因此我们把不合法的状态设置为-1。
状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积正好等于 j,所有的选法中,能挑选出来的最大价值。
状态转移方程:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])。
但是在使用 dp[i][j - v[i]] 的时候,不仅要判断 v[i] 表示的情况是否存在,也就是 j >= v[i],又要判断 dp[i][j - v[i]] != -1。这意味着,只有当体积 j-v[i] 是一个合法的状态(即之前已经计算过且不为-1)时,我们才能使用它来更新 dp[i][j]。
初始化:
我们多加一行,方便我们的初始化:
- 第一个格子为0,因为正好能凑齐体积为0的背包(即不选任何物品);
- 但是第一行后面的格子都是
-1,因为没有物品,无法满足体积大于0的情况。
填表顺序:
根据状态转移方程,我们仅需从上往下填表即可。注意,内层循环(即遍历体积 j 的循环)需要从小到大进行,以确保在计算 dp[i][j] 时,dp[i][j - v[i]] 已经被正确计算。
返回值:
由于最后可能凑不成体积为 V 的情况,因此返回之前需要特判一下。如果 dp[n][V] == -1,则表示无法凑成体积为 V 的背包,此时可以返回一个特定的值(如-1或0,具体取决于题目要求)来表示无解;否则,返回 dp[n][V] 即可。
- #include
- using namespace std;
-
- int main() {
- int n, V;
- cin >> n >> V;
- vector<int>v(n + 1);
- vector<int>w(n + 1);
- for (int i = 1; i <= n; i++) {
- cin >> v[i] >> w[i];
- }
- //解决第一问
- vector
int>>dp(n + 1, vector<int>(V + 1)); -
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= V; j++) {
- dp[i][j] = dp[i - 1][j];
- if (j >= v[i]) {
- dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
- }
- }
- }
- cout << dp[n][V] << endl;
-
- //解决第二问
- vector
int>>dp2(n + 1, vector<int>(V + 1)); - for (int i = 1; i <= V; i++) {
- dp2[0][i] = -1;
- }
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= V; j++) {
- dp2[i][j] = dp2[i - 1][j];
- if (j >= v[i] && dp2[i][j - v[i]] != -1) {
- dp2[i][j] = max(dp2[i - 1][j], dp2[i][j - v[i]] + w[i]);
- }
- }
- }
-
- if (dp2[n][V] != -1) {
- cout << dp2[n][V] << endl;
- } else {
- cout << 0 << endl;
- }
- }
优化版本
我们先看状态转移方程
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])
我们发现dp[i][j]的填写依赖于第i行和第i-1两行,这个优化策略和01背包就不太一样了
这就说明我们的这个dp[i][j - v[i]]要比dp[i][j]先更新好。所以遍历顺序是从左往右的。
除了这个遍历顺序,其他的和01区别没有区别
- #include
- using namespace std;
-
- int main() {
- int n, V;
- cin >> n >> V;
- vector<int>v(n + 1);
- vector<int>w(n + 1);
- for (int i = 1; i <= n; i++) {
- cin >> v[i] >> w[i];
- }
- //解决第一问
- vector<int>dp(V + 1,0);
-
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <=V ; j++) {
- if (j >= v[i]) {
- dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
- }
- }
- }
- cout << dp[V] << endl;
-
- //解决第二问
- vector<int>dp2(V + 1,0);
- for (int i = 1; i <= V; i++) {
- dp2[i] = -1;
- }
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <=V ; j++) {
- if (j >= v[i] && dp2[j - v[i]] != -1) {
- dp2[j] = max(dp2[j], dp2[j - v[i]] + w[i]);
- }
- }
- }
-
- if (dp2[V] != -1) {
- cout << dp2[V] << endl;
- } else {
- cout << 0 << endl;
- }
- }
题目二—— 322. 零钱兑换 - 力扣(LeetCode)


算法思路: 先将问题「转化」成我们熟悉的题型。
- i. 在⼀些物品中「挑选」⼀些出来,然后在满⾜某个「限定条件」下,解决⼀些问题,⼤概率 是「背包」模型;
- ii. 由于每⼀个物品都是⽆限多个的,因此是⼀个「完全背包」问题。 接下来的分析就是基于「完全背包」的⽅式来的。
1. 状态表⽰:
dp[i][j] 表⽰:从前 i 个硬币中挑选,总和正好等于 j ,所有的选法中,最少的硬币个 数。
2. 状态转移⽅程:
线性DP状态转移方程的分析方式,一般都是根据“最后一步”的状况来分情况讨论。在完全背包问题中,由于最后一个物品(硬币)能选很多个,因此我们需要分很多情况来考虑:
- i. 选0个第i个硬币:此时相当于就是从前i-1个硬币中挑选,总和正好等于j。因此,此时最少的硬币个数为dp[i-1][j]。
- ii. 选1个第i个硬币:此时相当于就是从前i-1个硬币中挑选,再加上1个第i个硬币,使得总和正好等于j。因为挑选了一个第i个硬币,所以我们很容易得到dp[i][j]=dp[i-1][j-coin[i]]+1;
- iii. 选2个第i个硬币:此时相当于就是从前i-1个硬币中挑选,再加上2个第i个硬币,使得总和正好等于j。因为挑选了2个第i个硬币,所以我们很容易得到dp[i][j]=dp[i-1][j-2*coin[i]]+2;
- ...(以此类推)
综上,我们的状态转移方程为:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-coin[i]]+1, dp[i-1][j-2*coin[i]]+2, ...)
但是,我们发现计算一个状态的时候,需要一个循环才能搞定,这很不高效。优化的方向就是用一个或者两个状态来表示这一堆的状态,通常就是用数学的方式做一下等价替换。
我们发现第二维 j 是有规律的变化的,因此我们去看看 dp[i][j-coin[i]] 这个状态:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-coin[i]]+1, dp[i-1][j-2*coin[i]]+2, ...)dp[i][j-coin[i]] = max(dp[i-1][j-coin[i]], dp[i-1][j-2*coin[i]]+1, dp[i-1][j-3*coin[i]]+2, ...)
我们发现,dp[i][j-coin[i]] 加上一个 1 正好和 dp[i][j] 中除了第一项以外的全部项一致,因此我们可以修改我们的状态转移方程为:
dp[i][j] = min(dp[i - 1][j], dp[i][j - coin[i]] + 1)
3. 初始化:
初始化第⼀⾏即可。
这⾥因为取 min,所以我们可以把⽆效的地⽅设置成⽆穷⼤ (0x3f3f3f3f)
至于我们为什么无穷大使用0x3f3f3f3f,这是因为使用INT_MAX会报错
因为这⾥要求正好凑成总和为 j ,因此,需要把第⼀⾏除了第⼀个位置的元素,都设置成⽆穷⼤。
4. 填表顺序:
根据「状态转移⽅程」,我们仅需「从上往下」填表即可。
5. 返回值:
根据「状态表⽰」,返回 dp[n][V] 。但是要特判⼀下,因为有可能凑不到。
- class Solution {
- public:
- int coinChange(vector<int>& coins, int amount) {
- int n = coins.size();
- const int INF = 0x3f3f3f3f;
- vector
int>> dp(n + 1, vector<int>(amount + 1,0)); - for (int j = 1; j <= amount; j++)
- dp[0][j] = INF;
-
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= amount; j++) {
- dp[i][j] = dp[i - 1][j];
- if (j >= coins[i - 1]) {
- dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i-1]] + 1);
- }
- }
- }
-
- if (dp[n][amount] != INF) {
- return dp[n][amount];
- } else {
- return -1;
- }
- }
- };
我们这里还是使用上面那个优化策略啊
- class Solution {
- public:
- int coinChange(vector<int>& coins, int amount) {
- int n = coins.size();
- const int INF = 0x3f3f3f3f;
- vector<int>dp(amount + 1,0);
- for (int j = 1; j <= amount; j++)
- dp[j] = INF;
-
- for (int i = 1; i <= n; i++) {
- for (int j = 0; j <= amount; j++) {
- if (j >= coins[i - 1]) {
- dp[j] = min(dp[j], dp[j-coins[i-1]] + 1);
- }
- }
- }
-
- if (dp[amount] != INF) {
- return dp[amount];
- } else {
- return -1;
- }
- }
- };
题目三——518. 零钱兑换 II - 力扣(LeetCode)


这题简单的一批。
首先,我们将问题转化为一个我们熟悉的题型。
- i. 当我们需要在一些物品中挑选一些出来,以满足某个限定条件并解决一些问题时,这大概率是一个背包模型问题。
- ii. 鉴于每一个物品都是无限多个的,因此,我们面对的是一个“完全背包”问题。
接下来的分析就是基于“完全背包”的解决方式。
状态表示:
dp[i][j] 表示从前 i 个硬币中挑选,总和正好等于 j 的组合方案数。
状态转移方程:
线性DP状态转移方程的分析方式,一般都是根据“最后一步”的状况来分情况讨论。由于最后一个物品(硬币)能选很多个,我们需要考虑多种情况:
- 选0个第
i 个硬币:此时相当于从前 i-1 个硬币中挑选,总和正好等于 j。因此,方案数为 dp[i-1][j]。 - 选1个第
i 个硬币:此时相当于从前 i-1 个硬币中挑选,总和正好等于 j-coins[i],然后再加上1个第 i 个硬币。因此此时dp[i][j]=dp[i-1][j-coin[i]]; - 选2个第
i 个硬币的情况类似,此时相当于从前 i-1 个硬币中挑选,总和正好等于 j-2*coins[i],然后再加上2个第 i 个硬币。因此此时dp[i][j]=dp[i-1][j-2*coin[i]]; - .......
综上,我们的状态转移方程为:
dp[i][j] = dp[i-1][j]+dp[i-1][j-coins[i]]+dp[i-1][j-2*coins[i]]...
但是,我们发现计算一个状态的时候,需要一个循环才能搞定,这很不高效。优化的方向就是用一个或者两个状态来表示这一堆的状态,通常就是用数学的方式做一下等价替换。
我们发现第二维 j 是有规律的变化的,因此我们去看看 dp[i][j-coin[i]] 这个状态:
dp[i][j] = dp[i-1][j]+dp[i-1][j-coins[i]]+dp[i-1][j-2*coins[i]]...dp[i][j-coins[i]] = dp[i-1][j-coins[i]]+dp[i-1][j-2*coins[i]]+dp[i-1][j-3*coins[i]]...
我们发现,dp[i][j-coin[i]] 正好和 dp[i][j] 中除了第一项以外的全部项一致,因此我们可以修改我们的状态转移方程为:
dp[i][j] = dp[i - 1][j]+dp[i][j-coins[i]]
- class Solution {
- public:
- int change(int amount, vector<int>& coins) {
- int n=coins.size();
- vector
int>>dp(n+1,vector<int>(amount+1,0)); - dp[0][0] = 1;
- for(int i=1;i<=n;i++)
- {
- for(int j=0;j<=amount;j++)
- {
- dp[i][j]=dp[i-1][j];
- if(j>=coins[i-1])
- {
- dp[i][j]+=dp[i][j-coins[i-1]];
- }
- }
- }
- return dp[n][amount];
- }
- };
我们优化一下
- class Solution {
- public:
- int change(int amount, vector<int>& coins) {
- int n=coins.size();
- vector<int>dp(amount+1,0);
- dp[0] = 1;
- for(int i=1;i<=n;i++)
- {
- for(int j=0;j<=amount;j++)
- {
- if(j>=coins[i-1])
- {
- dp[j]+=dp[j-coins[i-1]];
- }
- }
- }
- return dp[amount];
- }
- };
题目四——279. 完全平方数 - 力扣(LeetCode)


这题看起来好像很难,但是我们仔细看一下下面这个条件
1 <= n <= 10000
有没有发现是10000是100的平方数啊
嗯?那我们是不是可以搞一个数组,每个元素存放对应元素的平方。
- vector<int>nums(101);
- for(int i=1;i<=100;i++)
- {
- nums[i]=i*i;
- }
那我们这个题目不就变成了从nums[i]里面选择几个元素,使其的和等于n吗?
但是这个n也不一定是10000,所以我们完全可以再优化一下
- int s=sqrt(n);
- vector<int> nums(s+1);
- for (int i = 1; i <= s; i++) {
- nums[i] = i * i;
- }
现在这个题目是不是很熟悉?
首先,我们将问题转化为一个我们熟悉的题型。
- i. 当我们需要在一些物品中挑选一些出来,以满足某个限定条件并解决一些问题时,这大概率是一个背包模型问题。
- ii. 鉴于每一个物品都是无限多个的,因此,我们面对的是一个“完全背包”问题。
接下来的分析就是基于“完全背包”的解决方式。
状态表示:
dp[i][j] 表示从nums[1]到nums[i]里面,也就是从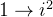 挑选,总和正好等于
挑选,总和正好等于 j 的组合方案数。
状态转移方程:
线性DP状态转移方程的分析方式,一般都是根据“最后一步”的状况来分情况讨论。由于最后一个物品(nums[i])能选很多个,我们需要考虑多种情况:
- 选0个nums[i](即不选
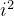 ):此时相当于从
):此时相当于从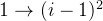 中挑选,总和正好等于
中挑选,总和正好等于 j。因此,方案数为 dp[i-1][j]。 - 选0个nums[i](即选1个
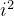 ):此时相当于从
):此时相当于从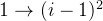 中挑选,总和正好等于
中挑选,总和正好等于 j-nums[i]。因此,方案数为 dp[i-1][j-nums[i]]+1。 - 选0个nums[i](即选1个
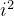 ):此时相当于从
):此时相当于从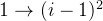 中挑选,总和正好等于
中挑选,总和正好等于 j-2*nums[i]。因此,方案数为 dp[i-1][j-2*nums[i]]+2。 - .......
综上,我们的状态转移方程为:
dp[i][j] = min(dp[i-1][j],dp[i-1][j-nums[i]+1,dp[i-1][j-2*nums[i]]+2,....);
但是,我们发现计算一个状态的时候,需要一个循环才能搞定,这很不高效。优化的方向就是用一个或者两个状态来表示这一堆的状态,通常就是用数学的方式做一下等价替换。
我们发现第二维 j 是有规律的变化的,因此我们去看看 dp[i][j-nums[i]] 这个状态:
dp[i][j] = min(dp[i-1][j],dp[i-1][j-nums[i]]+1,dp[i-1][j-2*nums[i]]+2,....);dp[i][j-nums[i]] = min(dp[i-1][j-nums[i]],dp[i-1][j-2*nums[i]]+1,dp[i-1][j-3*nums[i]]+2,....);
我们发现,dp[i][j-nums[i]]+1 正好和 dp[i][j] 中除了第一项以外的全部项一致,因此我们可以修改我们的状态转移方程为:
dp[i][j] = min(dp[i - 1][j],dp[i][j-coins[i]]+1)
但是由于这个dp[i][j-coins[i]]+1不一定存在,所以我们需要特判一下。
3. 初始化:
初始化第⼀⾏即可。
这⾥因为取 min,所以我们可以把⽆效的地⽅设置成⽆穷⼤ (0x3f3f3f3f)
至于我们为什么无穷大使用0x3f3f3f3f,这是因为使用INT_MAX会报错
因为这⾥要求正好凑成总和为 j ,因此,需要把第⼀⾏除了第⼀个位置的元素,都设置成⽆穷⼤。
4. 填表顺序:
根据「状态转移⽅程」,我们仅需「从上往下」填表即可。
5. 返回值:
根据「状态表⽰」,返回 dp[s][n] 。
- class Solution {
- public:
- int numSquares(int n) {
- const int INF=0x3f3f3f3f;
- //1.初始化原数组
- int s=sqrt(n);
- vector<int> nums(s+1);
- for (int i = 1; i <= s; i++) {
- nums[i] = i * i;
- }
- //2.动态规划
- vector
int>> dp(s+1, vector<int>(n+1, 0)); - for (int i = 1; i <= n; i++) {
- dp[0][i] = INF;
- }
- for (int i = 1; i <= s; i++) {
- for (int j = 0; j <= n; j++) {
- dp[i][j] = dp[i - 1][j];
- if (j >= nums[i]&&dp[i][j-nums[i]!=INF]) {
- dp[i][j] = min(dp[i][j], dp[i][j - nums[i]]+1);
- }
- }
- }
- return dp[s][n];
- }
- };
优化版本
其实优化版本和之前的很像。
- class Solution {
- public:
- int numSquares(int n) {
- const int INF=0x3f3f3f3f;
- //1.初始化原数组
- int s=sqrt(n);
- vector<int> nums(s+1);
- for (int i = 1; i <= s; i++) {
- nums[i] = i * i;
- }
- //2.动态规划
- vector<int>dp(n+1, 0);
- for (int i = 1; i <= n; i++) {
- dp[i] = INF;
- }
- for (int i = 1; i <= s; i++) {
- for (int j = 0; j <= n; j++) {
- if (j >= nums[i]&&dp[j-nums[i]!=INF]) {
- dp[j] = min(dp[j], dp[j - nums[i]]+1);
- }
- }
- }
- return dp[n];
- }
- };
三 . 二维背包的费用问题
题目一——474. 一和零 - 力扣(LeetCode)


首先,我们需要将这个问题转化为我们熟悉的题型。观察题目要求,我们发现它符合背包问题的基本特征:
-
在一些物品(这里是字符串)中挑选一些出来,以满足某个限定条件(这里是字符'0'和字符'1'的个数限制),并解决一些问题(这里是求最大的长度)。因此,这个问题大概率是一个背包模型。
-
由于每一个物品(字符串)都只有一个,不能拆分或重复使用,因此这是一个“01背包问题”。
然而,与常规的01背包问题不同的是,这道题有两个限制条件:字符'0'的个数和字符'1'的个数。因此,它是一个“二维费用的01背包问题”。为了解决这个问题,我们需要定义一个三维的dp表,将第二个限制条件也考虑进去。
1.状态表示:
我们使用dp[i][j][k]来表示从前i个字符串中挑选,字符'0'的个数不超过j,字符'1'的个数不超过k,所有的选法中最大的长度。
2.状态转移方程:
线性dp问题的状态转移方程一般根据“最后一步”的状况来分情况讨论。为了方便叙述,我们记第i个字符中,字符'0'的个数为a,字符'1'的个数为b。
-
不选第i个字符串:这种情况下,我们相当于就是去前i-1个字符串中挑选,字符'0'的个数不超过j,字符'1'的个数不超过k。此时的最大长度为dp[i-1][j][k]。
-
选择第i个字符串:这种情况下,我们需要在前i-1个字符串中挑选,字符'0'的个数不超过j-a,字符'1'的个数不超过k-b。然后,在这个挑选出来的最长长度后面加上字符串i的长度(即1,因为每个字符串的长度为1)。此时的最大长度为dp[i-1][j-a][k-b] + 1。但是,这种状态不一定存在(即j-a或k-b可能为负数,表示无法满足限制条件),因此需要特判一下。
综上,状态转移方程为:
dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-a][k-b] + 1) (当j-a >= 0且k-b >= 0时)
dp[i][j][k] = dp[i-1][j][k] (当不选择第i个字符串时)
注意,在实际编程中,我们可以先初始化dp[i][j][k]为dp[i-1][j][k],然后再尝试更新为dp[i-1][j-a][k-b] + 1(如果满足条件)。
3.初始化:
当没有字符串的时候,没有长度可言,因此我们将dp表的所有元素初始化为0即可。
4.填表顺序:
由于状态转移方程中涉及到了i-1的状态,因此我们需要保证第一维的循环从小到大进行。即先计算dp[0][...][...],再计算dp[1][...][...],以此类推。
5.返回值:
根据状态表示,我们返回dp[len][m][n]的值。其中len表示字符串数组的长度,m和n分别表示字符'0'和字符'1'的个数限制。这个值表示在给定限制条件下,从前len个字符串中挑选出来的最大长度。
- class Solution {
- public:
- int findMaxForm(vector
& strs, int m, int n) { - int len=strs.size();
- vector
int>>> dp(len + 1, vectorint>>(m + 1, vector<int>(n + 1, 0))); - for(int i=1;i<=len;i++)
- {
- // 统计⼀下 0 1 的个数
- int a = 0, b = 0;
- for(auto ch : strs[i - 1])
- {
- if(ch == '0')
- {
- a++;
- }
- else
- {
- b++;
- }
- }
-
- //进行动态规划
- for(int j=0;j<=m;j++)
- {
- for(int k=0;k<=n;k++)
- {
- dp[i][j][k]=dp[i-1][j][k];
- if(j>=a&&k>=b)
- {
- dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-a][k-b] + 1);
- }
- }
- }
- }
- return dp[len][m][n];
- }
- };
我们可以对其进行优化,优化策略就是
- 三维变二维
- 遍历顺序改为从右往左
这和01背包的完全一样。
- class Solution {
- public:
- int findMaxForm(vector
& strs, int m, int n) { - int len=strs.size();
- vector
int>>dp(m + 1, vector<int>(n + 1, 0)); - for(int i=1;i<=len;i++)
- {
- // 统计⼀下 0 1 的个数
- int a = 0, b = 0;
- for(auto ch : strs[i - 1])
- {
- if(ch == '0')
- {
- a++;
- }
- else
- {
- b++;
- }
- }
-
- //进行动态规划
- for(int j=m;j>=0;j--)
- {
- for(int k=n;k>=0;k--)
- {
- if(j>=a&&k>=b)
- {
- dp[j][k]=max(dp[j][k],dp[j-a][k-b] + 1);
- }
- }
- }
- }
- return dp[m][n];
- }
- };
题目二——879. 盈利计划 - 力扣(LeetCode)


这道题目非常难读懂,但是如果结合例子多读几遍,你就会发现它其实是一个经典的“二维费用的背包问题”。因此,我们可以仿照“二维费用的背包”来定义状态表示。
1. 状态表示:
我们使用dp[i][j][k]来表示从前i个计划中挑选,总人数不超过j,总利润至少为k,一共有多少种选法。
这里需要特别注意,题目中出现了“至少”这一条件,和我们之前做过的背包问题不一样。因此,在分析状态转移方程的时候,我们要结合实际情况进行考虑。
2. 状态转移方程:
根据“最后一个位置”的元素,结合题目的要求,我们有“选择”最后一个元素或者“不选择”最后一个元素两种策略:
-
不选第i个位置的计划:那我们只能去前i-1个计划中挑选,总人数不超过j,总利润至少为k。此时一共有dp[i-1][j][k]种选法。
-
选择第i个位置的计划:那我们在前i-1个计划中挑选的时候,限制就变成了总人数不超过j-g[i],总利润至少为k-p[i]。此时一共有dp[i-1][j-group[i]][max(0, k-profit[i])]种选法。
这里有两个细节需要注意:
-
如果j-group[i] < 0,此时说明g[i]过大,也就是人数过多。因为我们的状态表示要求人数不能超过j,因此这个状态是不合法的,需要舍去。
-
如果k-profit[i] < 0,此时说明p[i]过大,也就是利润太高。但是利润高,正是我们想要的。因此,这个状态不能舍去。然而,我们的dp表没有负数的下标,这就意味着这些状态我们无法直接表示。其实,根本不需要负的下标,我们根据实际情况来看,如果这个任务的利润已经能够达标了(即使减去当前任务的利润后小于0),我们仅需在之前的任务中挑选出来的利润至少为0就可以了。因为实际情况不允许负利润,那么负利润就等价于利润至少为0的情况。
综上,我们的状态转移方程为:
dp[i][j][k] = dp[i-1][j][k] + dp[i-1][j-group[i-1]][max(0, k-profit[i-1])]
注意,这里dp[i][j][0]可以通过对k的遍历来逐步计算得出。
3. 初始化:
当没有任务的时候,我们的利润为0,此时无论人数限制为多少,我们都能找到一个“空集”的方案。因此,初始化dp[0][j][0]的位置为1,其中0 <= j <= n(n为人数上限)。
4. 填表顺序:
根据状态转移方程,我们保证i从小到大即可。同时,对于每个i,我们需要对j和k进行遍历来填充dp表。
5. 返回值:
根据状态表示,我们返回dp[len][m][n]的值,其中len表示字符串数组(或任务列表)的长度,m和n分别表示人数和利润的限制。这个值表示在给定的人数和利润限制下,从前len个计划中挑选的总选法数量。
- class Solution {
- public:
- int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
- const int MOD = 1e9 + 7; // 注意结果取模
- int len = group.size();
- vector
int>>> dp(len + 1, vectorint>>(n+1,vector<int>(minProfit+1))); - for(int j = 0; j <= n; j++) dp[0][j][0] = 1; // 初始化
- for(int i=1;i<=len;i++)
- {
- for(int j=0;j<=n;j++)
- {
- for(int k=0;k<=minProfit;k++)
- {
- dp[i][j][k] = dp[i-1][j][k];
- if(j>=group[i-1])
- {
- dp[i][j][k] = dp[i-1][j][k] + dp[i-1][j-group[i-1]][max(0, k-profit[i-1])];
- }
- dp[i][j][k] %= MOD; // 注意结果取模;
- }
- }
- }
- return dp[len][n][minProfit];
- }
- };
这个优化思路和01背包的是一模一样的啊
- class Solution {
- public:
- int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
- const int MOD = 1e9 + 7; // 注意结果取模
- int len = group.size();
- vector
int>>dp(n+1,vector<int>(minProfit+1)); - for(int j = 0; j <= n; j++) dp[j][0] = 1; // 初始化
- for(int i=1;i<=len;i++)
- {
- for(int j=n;j>=0;j--)
- {
- for(int k=minProfit;k>=0;k--)
- {
- if(j>=group[i-1])
- {
- dp[j][k] +=dp[j-group[i-1]][max(0, k-profit[i-1])];
- }
- dp[j][k] %= MOD; // 注意结果取模;
- }
- }
- }
- return dp[n][minProfit];
- }
- };
四 . 其他问题
题目一——377. 组合总和 Ⅳ - 力扣(LeetCode)


这题似包非包。
一定要注意,我们的背包问题本质上求的是「组合」数问题,而这一道题求的是「排列数」问题。因此我们不能被这道题给迷惑,还是用常规的动态规划(DP)思想来解决这道题。
状态表示:
这道题的状态表示就是根据「拆分出相同子问题」的方式,抽象出来一个状态表示:当我们在求target这个数一共有几种排列方式的时候,对于最后一个位置,如果我们拿出数组中的一个数x,接下来就是去找target - x一共有多少种排列方式。
因此我们可以抽象出来一个状态表示:dp[i]表示:总和为i的时候,一共有多少种排列方案。
状态转移方程:
对于dp[i],我们根据「最后一个位置」划分,我们可以选择数组中的任意一个数nums[j],其中0 <= j <= n - 1。
当nums[j] <= target的时候,此时的排列数等于我们先找到target - nums[j]的排列方案数,然后在每一个方案后面加上一个数字nums[j]。因为有很多个j符合情况,因此我们的状态转移方程为:
dp[i] += dp[target - nums[j]],其中0 <= j <= n - 1且nums[j] <= target。
初始化:
当和为0的时候,我们可以什么都不选,「空集」一种方案,因此dp[0] = 1。
填表顺序:
根据「状态转移方程」易得「从左往右」。
返回值:
根据「状态表示」,我们要返回的是dp[target]的值。
- class Solution {
- public:
- int combinationSum4(vector<int>& nums, int target) {
- vector<double> dp(target + 1);
- dp[0] = 1;
- for (int i = 1; i <= target; i++)
- for (auto x : nums)
- if (x <= i)
- dp[i] += dp[i - x];
- return dp[target];
- }
- };


评论记录:
回复评论: