计算机视觉——相机标定(Camera Calibration)

id="article_content" class="article_content clearfix" style="height: 2000px; overflow: hidden;"> id="content_views" class="markdown_views prism-atom-one-dark">

class="toc">

文章目录


在进行机器人视觉相关项目的过程中，首先要进行相机标定，此博客记录相机标定的相关原概念及实施方法。

1. 简介

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定。相机标定是非常关键的环节。

  • 进行摄像机标定的目的：求出相机的内、外参数，以及畸变参数。
  • 标定相机后通常是想做两件事：一个是由于每个镜头的畸变程度各不相同，通过相机标定可以校正这种镜头畸变矫正畸变，生成矫正后的图像；另一个是根据获得的图像重构三维场景。

2. 原理

相机标定的基本原理是通过已知的三维世界坐标系中的点和对应的二维图像坐标系中的点，建立一个数学模型，将三维世界坐标系中的点投影到二维图像坐标系中。这个数学模型通常包括以下几个部分：

  1. 相机内参矩阵（Intrinsic Matrix）：描述相机的内部几何特性，包括焦距、主点坐标等。
  2. 畸变系数（Distortion Coefficients）：描述图像畸变，包括径向畸变和切向畸变。
  3. 旋转矩阵和平移向量（Rotation Matrix and Translation Vector）：描述相机在世界坐标系中的姿态，也可以叫做外参数。

常用标定步骤：

  1. 准备标定板：使用一个已知尺寸的标定板（如棋盘格），并拍摄多张不同角度和位置的图像。
  2. 检测角点：在每张图像中检测标定板的角点，并记录其二维图像坐标。
  3. 生成世界坐标：根据标定板的尺寸，生成标定板角点的三维世界坐标。
  4. 计算内参和畸变系数：使用检测到的角点和生成的世界坐标，计算相机的内参矩阵和畸变系数。
  5. 计算旋转矩阵和平移向量：计算每张图像的旋转矩阵和平移向量。
  6. 计算重投影误差：将世界坐标系中的点投影到图像坐标系中，并与实际检测到的图像坐标进行比较，计算重投影误差。

常用术语

内参矩阵: Intrinsic Matrix
焦距: Focal Length
主点: Principal Point
角点: Corner Point
径向畸变: Radial Distortion
切向畸变: Tangential Distortion
旋转矩阵: Rotation Matrices
平移向量: Translation Vectors
平均重投影误差: Mean Reprojection Error
重投影误差: Reprojection Errors
重投影点: Reprojected Points

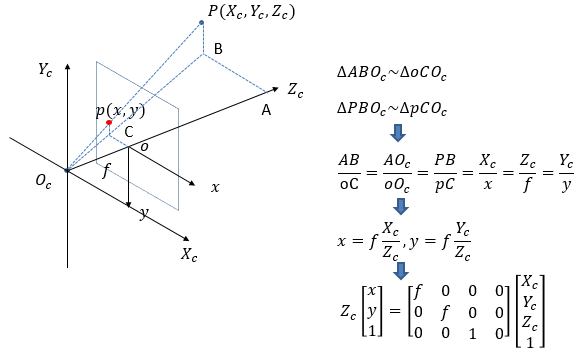
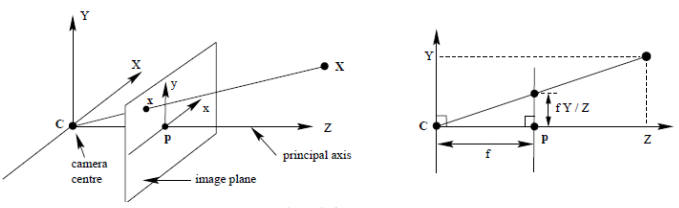
3. 相机模型

3.1 四大坐标系

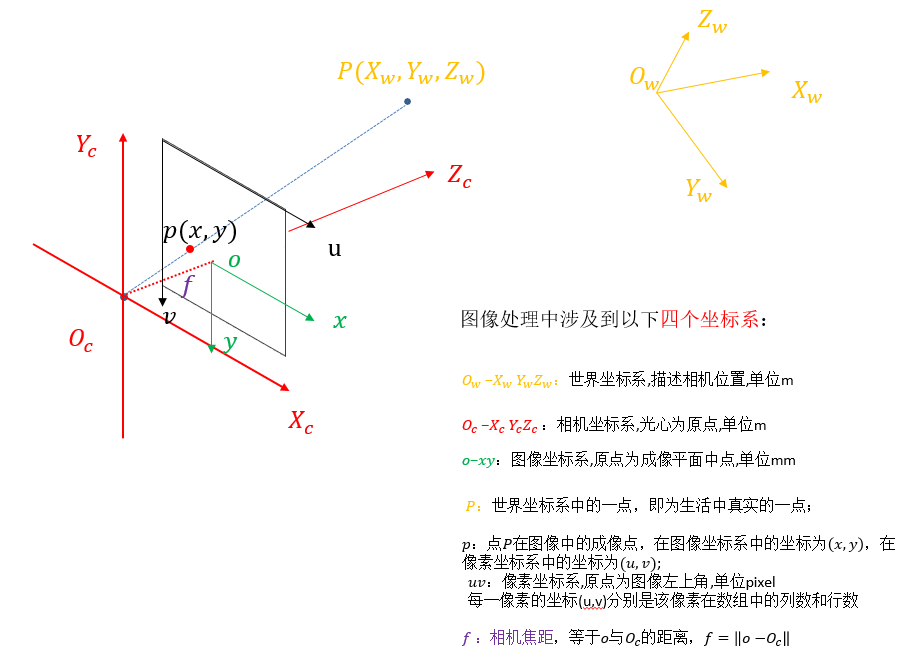在这里插入图片描述世界坐标系是一个全局坐标系，用于描述物体在真实世界中的位置。世界坐标系用 (X_w, Y_w, Z_w) 表示，独立于相机，可以任意选择原点和坐标轴的方向。

**相机坐标系 (Camera Coordinate System)**以相机的光学中心为原点， Z Z Z轴指向相机的正前方， X X X轴和 Y Y Y轴分别指向相机的右侧和下方，用于描述物体在相机视角下的位置。通常，相机坐标系用 ( X c , Y c , Z c ) (X_c, Y_c, Z_c) (Xc​,Yc​,Zc​) 表示。

**图像坐标系 (Image Coordinate System)**是二维坐标系，用于描述物体在相机成像平面上的投影位置。通常，图像坐标系用 ( x , y ) (x, y) (x,y)表示，图像坐标系的原点通常位于成像平面的中心， x x x轴和 y y y轴分别指向图像的右侧和下方。

**像素坐标系 (Pixel Coordinate System)**是二维坐标系，用于描述物体在数字图像中的像素位置。通常，像素坐标系用 ( u , v ) (u, v) (u,v) 表示，即列数和行数。像素坐标系的原点通常位于图像的左上角， u u u轴和 v v v轴分别指向图像的右侧和下方。

3.2 坐标系间的转换关系

3.2.1 世界坐标系到相机坐标系

世界坐标系到相机坐标系的转换通常通过一个刚体变换（旋转和平移）来实现。这个变换可以用一个4x4的变换矩阵 T w c T_{wc} Twc​ 表示，包含旋转矩阵 R R R和平移向量 t t t

[ X c Y c Z c 1 ] = T w c [ X w Y w Z w 1 ] = [ R t 0 1 ] [ X w Y w Z w 1 ] [XcYcZc1] class="MathJax_Display MathJax_Processed">⎡⎣⎢⎢⎢XcYcZc1⎤⎦⎥⎥⎥

=T_{wc}[XwYwZw1] class="MathJax_Display MathJax_Processed">⎡⎣⎢⎢⎢XwYwZw1⎤⎦⎥⎥⎥
=[Rt01] class="MathJax_Display MathJax_Processed">[R0t1]
[XwYwZw1] class="MathJax_Display MathJax_Processing">
​Xc​Yc​Zc​1​ ​=Twc​ ​Xw​Yw​Zw​1​ ​=[R0​t1​] ​Xw​Yw​Zw​1​ ​

3.2.2 相机坐标系到图像坐标系

img

相机坐标系到图像坐标系的转换是通过透视投影实现的。假设相机焦距为 f f f，则成像面是与 X c O Y c X_cOY_c Xc​OYc​平面平行且距离为 f f f的平面，在相机坐标系中， p ( x c , y c , z c ) p(x_c,y_c,z_c) p(xc​,yc​,zc​)，在图像坐标系中的成像点是 p ′ ( x , y ) p'(x,y) p′(x,y)

img

利用相似三角形求得： x x c = y y c = f z c \frac{x}{x_c}=\frac{y}{y_c}=\frac{f}{z_c} xc​x​=yc​y​=zc​f​

即 x = f z c ⋅ x c x=\frac{f}{z_c}\cdot x_c x=zc​f​⋅xc​, y = f z c ⋅ y c y=\frac{f}{z_c}\cdot y_c y=zc​f​⋅yc​，写为矩阵形式：
[ x y 1 ] = [ f z c 0 0 0 0 f z c 0 0 0 0 1 z c 0 ] ⋅ [ x c y c z c 1 ] [xy1] class="MathJax_Display MathJax_Processing">

=[fzc0000fzc00001zc0] class="MathJax_Display MathJax_Processing"> \cdot [xcyczc1] class="MathJax_Display MathJax_Processing"> ​xy1​ ​= ​zc​f​00​0zc​f​0​00zc​1​​000​ ​⋅ ​xc​yc​zc​1​ ​
也可以写作：
z c ⋅ [ x y 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] ⋅ [ x c y c z c 1 ] z_c \cdot [xy1] class="MathJax_Display MathJax_Processing">=[f0000f000010] class="MathJax_Display MathJax_Processing"> \cdot [xcyczc1] class="MathJax_Display MathJax_Processing"> zc​⋅ ​xy1​ ​= ​f00​0f0​001​000​ ​⋅ ​xc​yc​zc​1​ ​

3.2.3 像素坐标系转换为图像坐标系

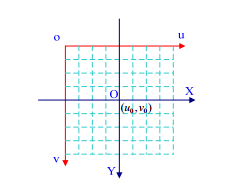在这里插入图片描述像素坐标系uov是一个二维直角坐标系，反映了相机CCD/CMOS芯片中像素的排列情况。原点o位于图像的左上角，u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素（整数）。

像素坐标系不利于坐标变换，因此需要建立图像坐标系XOY，其坐标轴的单位通常为毫米（mm），原点是相机光轴与相面的交点（称为主点），即图像的中心点，X轴、Y轴分别与u轴、v轴平行。故两个坐标系实际是平移关系，即可以通过平移就可得到。
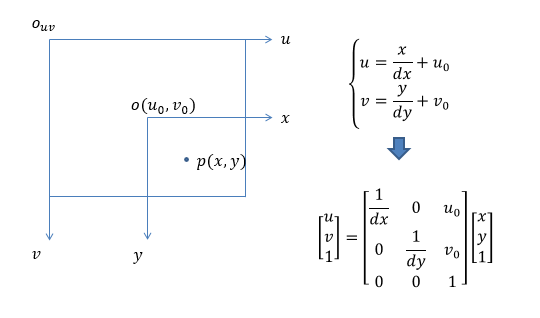在这里插入图片描述其中， d x dx dx、 d y dy dy分别为像素在 x x x、 y y y轴方向上的物理尺寸， u 0 u_0 u0​, v 0 v_0 v0​为主点（图像坐标系原点）坐标。

3.2.4 世界坐标转换为像素坐标

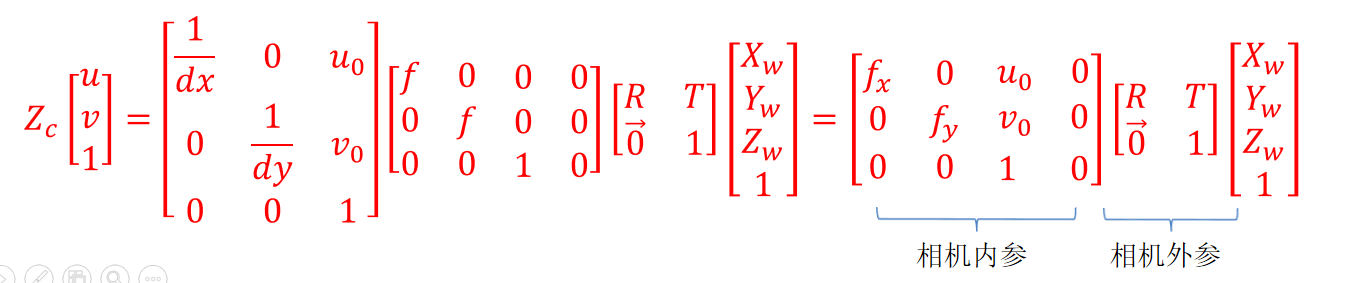
在这里插入图片描述

3.3 畸变

3.3.1 畸变类型

在这里插入图片描述

3.3.1.1 径向畸变（Radial Distortion）

径向畸变是由于镜头的形状引起的，通常表现为图像中心区域的放大或缩小。径向畸变可以进一步分为两种类型：

x corrected = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y corrected = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) x_{\text{corrected}} = x(1 + k_1 r^2 + k_2 r^4 + k_3 r^6)\\ y_{\text{corrected}} = y(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) xcorrected​=x(1+k1​r2+k2​r4+k3​r6)ycorrected​=y(1+k1​r2+k2​r4+k3​r6)
其中：

3.3.1.2 切向畸变（Tangential Distortion）

切向畸变是由于镜头和成像平面不完全平行引起的。这种畸变会导致图像中的某些区域相对于其他区域发生偏移。切向畸变可以用以下公式描述：

x corrected = x + [ 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) ] y corrected = y + [ p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y ] x_{\text{corrected}} = x + [2p_1 xy + p_2(r^2 + 2x^2)] \\ y_{\text{corrected}} = y + [p_1(r^2 + 2y^2) + 2p_2 xy] xcorrected​=x+[2p1​xy+p2​(r2+2x2)]ycorrected​=y+[p1​(r2+2y2)+2p2​xy]

其中, p 1 , p 2 p_1, p_2 p1​,p2​ 是切向畸变系数。

3.3.2 畸变模型

综合径向畸变和切向畸变，完整的畸变模型可以表示为：
x corrected = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + [ 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) ] y corrected = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + [ p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y ] x_{\text{corrected}} = x(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + [2p_1 xy + p_2(r^2 + 2x^2)] \\ y_{\text{corrected}} = y(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + [p_1(r^2 + 2y^2) + 2p_2 xy] xcorrected​=x(1+k1​r2+k2​r4+k3​r6)+[2p1​xy+p2​(r2+2x2)]ycorrected​=y(1+k1​r2+k2​r4+k3​r6)+[p1​(r2+2y2)+2p2​xy]

在相机标定过程中，通过拍摄已知几何形状的标定板（如棋盘格），可以计算出畸变系数 k 1 , k 2 , k 3 , p 1 , p 2 k_1, k_2, k_3, p_1, p_2 k1​,k2​,k3​,p1​,p2​。然后，利用这些系数对图像进行畸变校正，恢复图像的几何形状。

注：本文转载自blog.csdn.net的TunnyLand的文章"https://blog.csdn.net/qq_42875127/article/details/144251463"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！