今天学习一种新的数据结构——栈

1.栈的概念及结构

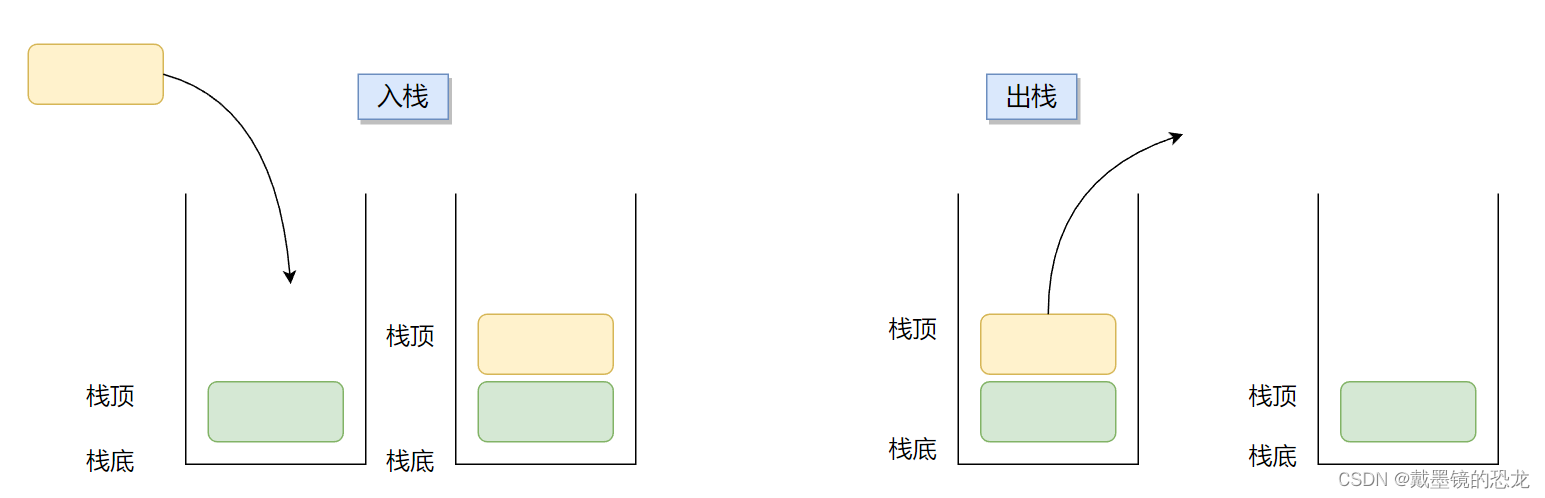
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

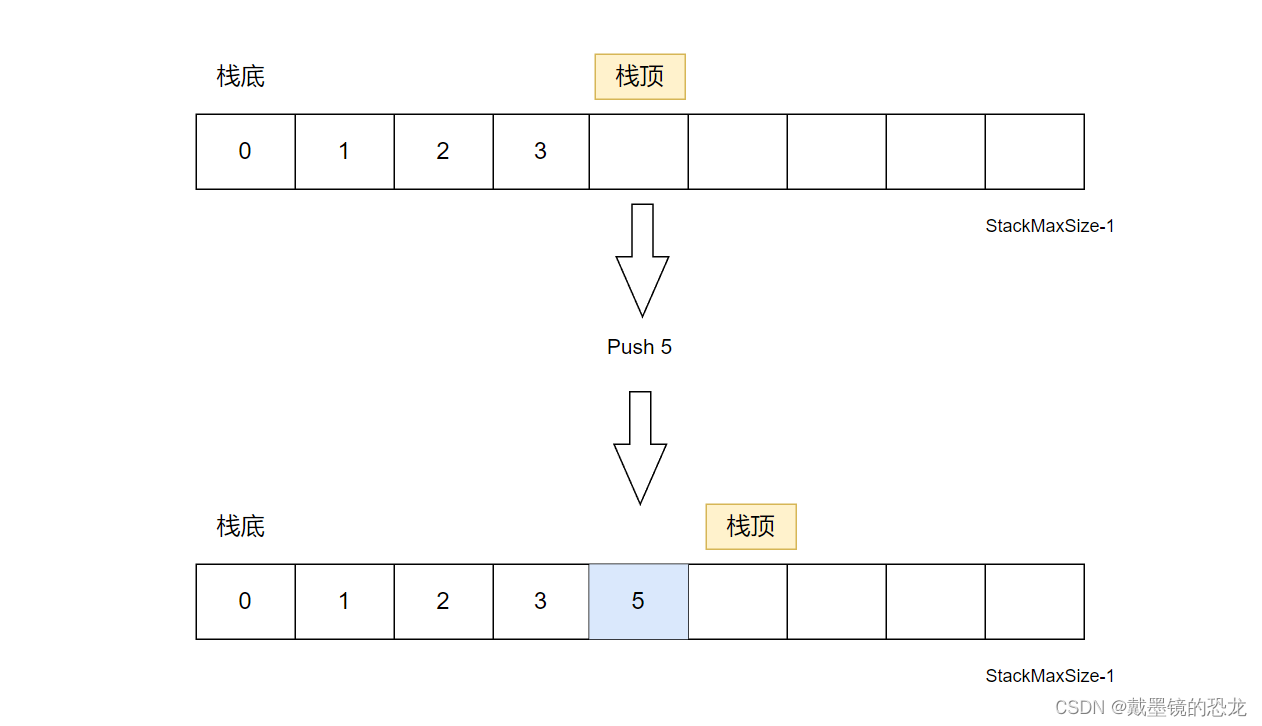
栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小

typedef int StackDataType;
//动态
typedef struct Stack
{
	StackDataType* arr;//数组实现
	int top;//栈顶，有效元素的下一个
	int capacity;//数组容量
}Stack;
1
2
3
4
5
6
7
8

2.栈的实现

栈这种数据结构的特点就是后进先出，由于它的特性，它的使用方法也就不像链表那样麻烦。基本使用如下：

2.1初始化

//初始化
void StackInit(Stack* ps)
{
	assert(ps);
	ps->arr = NULL;
	ps->capacity = 0;
	ps->top = 0;
}
1
2
3
4
5
6
7
8

2.2入栈

入栈前，应检查数组的大小。若数组满了，应进行扩容。

//入栈
void StackPush(Stack* ps, StackDataType x)
{
	assert(ps);
	//检查容量
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		//扩容
		StackDataType* tmp = (StackDataType*)realloc(ps->arr, sizeof(StackDataType) * newcapacity);
		if (!tmp)
		{
			perror("realloc");
			return;
		}
		ps->arr = tmp;
		ps->capacity = newcapacity;
	}
	//数据入栈
	ps->arr[ps->top] = x;
	ps->top++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.3出栈

由于我们使用的是数组，所以出栈就非常简单，只需将栈顶下移即可。

//出栈
void StackPop(Stack* ps)
{
	assert(ps);
	//栈中得有元素
	assert(ps->top);
	//出栈
	ps->top--;
}
1
2
3
4
5
6
7
8
9

2.4栈顶元素

//栈顶元素
StackDataType StackTopElement(Stack* ps)
{
	assert(ps);
	assert(ps->top);
	return ps->arr[ps->top - 1];
}
1
2
3
4
5
6
7

2.5栈中有效元素个数

由于数组下标从0开始，我们的栈顶指向的是当前元素的下一个位置；因此，直接返回栈顶即可。

//有效元素个数
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;
}
1
2
3
4
5
6

2.6检测栈是否为空

如果为空返回非零结果，如果不为空返回0

//是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);

	return ps->top == 0;
}
1
2
3
4
5
6
7

2.7销毁栈

//销毁栈
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->arr);
	ps->arr = NULL;
	ps->capacity = 0;
	ps->top = 0;
}
1
2
3
4
5
6
7
8
9

2.8栈的打印

由于栈的特性，它的打印方式和数组不同。它是先获取栈顶元素打印，然后出栈。

int main()
{
	Stack stack;
	StackInit(&stack);
	StackPush(&stack, 1);
	StackPush(&stack, 2);
	StackPush(&stack, 3);
	StackPush(&stack, 4);
	StackPush(&stack, 5);

	while (!StackEmpty(&stack))
	{
		int top = StackTopElement(&stack);
		printf("%d ", top);
		StackPop(&stack);
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18