MATLAB中均值、方差、标准差、协方差、相关性的计算

  1. 公式

1.均值

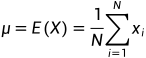
2.方差

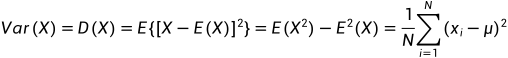
3.标准差\均方差

4.协方差

5.相关性

6.加权均值

7.加权方差

8.加权标准差

  1. MATLAB代码

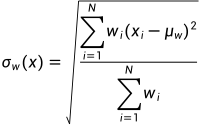
样本定义

  1. %%
  2. x=[1 2 3 3 2 1]'
  3. y = [1 2 3 3 1 2]'
  4. z= 3+2*y

1.均值

  1. %% 均值
  2. xmean=mean(x)
  3. sum(x)/size(x,1)
xmean =
2
ans =
2

2.方差

  1. %% 方差（n，可修改）
  2. xvar=var(x,1)
  3. sum((x-xmean).^2)/size(x,1)%定义
  4. %% 方差（n-1，可修改）
  5. xvar_1=var(x)
  6. sum((x-xmean).^2)/[size(x,1)-1]%定义
  7. %% 根据公式推导：E(X²)-E²(X)
  8. mean(x.^2)-[mean(x)]^2
xvar =
0.6667

ans =
0.6667

xvar_1 =
0.8000

ans =
0.8000

ans =
0.6667

3.标准差\均方差

  1. %% 标准差（n，可修改）
  2. xstd=std(x,1)
  3. sqrt( sum((x-xmean).^2)/size(x,1) )%定义
  4. sqrt( var(x,1) )
  5. %% 标准差（n-1，可修改）
  6. xstd_1=std(x)
  7. sqrt(sum((x-xmean).^2)/(size(x,1)-1))%定义
  8. sqrt( var(x) )
xstd =
0.8165

ans =
0.8165

ans =
0.8165

xstd_1 =
0.8944

ans =
0.8944

ans =
0.8944

4.协方差

  1. %% 协方差（n，可修改）
  2. xcov = cov(x,1)%单个向量的协方差=方差
  3. xycov = cov(x,y,1)
  4. [(x-xmean)']*[y-mean(y)]/size(x,1)%定义
  5. %% 协方差（n-1，可修改）
  6. xcov_1 = cov(x)%单个向量的协方差=方差
  7. xycov_1 = cov(x,y)
  8. [(x-xmean)']*[y-mean(y)]/(size(x,1)-1)%定义
xcov =
0.6667

xycov =
0.6667 0.5000
0.5000 0.6667

ans =
0.5000

xcov_1 =
0.8000

xycov_1 =
0.8000 0.6000
0.6000 0.8000

ans =
0.6000

5.相关性

  1. %% 相关系数
  2. xycorrcoef = corrcoef(x,y)
  3. xzcorrcoef = corrcoef(x,z)
  4. yzcorrcoef = corrcoef(y,z)
  5. corrcoef([x,y,z])
xycorrcoef =
1.0000 0.7500
0.7500 1.0000

xzcorrcoef =
1.0000 0.7500
0.7500 1.0000

yzcorrcoef =
1 1
1 1

ans =
1.0000 0.7500 0.7500
0.7500 1.0000 1.0000
0.7500 1.0000 1.0000

6.加权均值

  1. %% 加权均值
  2. miu_w=x'*y/sum(y)
miu_w =
2.2500

7.加权方差

  1. %% 加权方差
  2. xy_var=var(x,y)
  3. xy_var2=[(x-miu_w).^2]'*y/sum(y)
xy_var =
0.6875


xy_var2 =
0.6875

8.加权标准差

  1. %% 加权标准差
  2. xy_std=std(x,y)
  3. xy_std2=sqrt(xy_var2)
xy_std =
0.8292

xy_std2 =
0.8292

3.完整代码

  1. %%
  2. disp("样本")
  3. x=[1 2 3 3 2 1]'
  4. y = [1 2 3 3 1 2]'
  5. z= 3+2*y
  6.  
  7. %% 均值
  8. disp("均值")
  9. xmean=mean(x)
  10. sum(x)/size(x,1)
  11.  
  12.  
  13. %% 方差（n，可修改）
  14. disp("方差（n，可修改）")
  15. xvar=var(x,1)
  16. sum((x-xmean).^2)/size(x,1)%定义
  17. %% 方差（n-1，可修改）
  18. disp("方差（n-1，可修改）")
  19. xvar_1=var(x)
  20. sum((x-xmean).^2)/[size(x,1)-1]%定义
  21. %% 根据公式推导：E(X²)-E²(X)
  22. disp("公式推导：E(X²)-E²(X)")
  23. mean(x.^2)-[mean(x)]^2
  24.  
  25.  
  26. %% 标准差（n，可修改）
  27. disp("标准差（n，可修改）")
  28. xstd=std(x,1)
  29. sqrt( sum((x-xmean).^2)/size(x,1) )%定义
  30. sqrt( var(x,1) )
  31. %% 标准差（n-1，可修改）
  32. disp("标准差（n-1，可修改）")
  33. xstd_1=std(x)
  34. sqrt(sum((x-xmean).^2)/(size(x,1)-1))%定义
  35. sqrt( var(x) )
  36.  
  37.  
  38. %% 协方差（n，可修改）
  39. disp("协方差（n，可修改）")
  40. xcov = cov(x,1)%单个向量的协方差=方差
  41. xycov = cov(x,y,1)
  42. [(x-xmean)']*[y-mean(y)]/size(x,1)%定义
  43. %% 协方差（n-1，可修改）
  44. disp("协方差（n-1，可修改）")
  45. xcov_1 = cov(x)%单个向量的协方差=方差
  46. xycov_1 = cov(x,y)
  47. [(x-xmean)']*[y-mean(y)]/(size(x,1)-1)%定义
  48.  
  49.  
  50. %% 相关系数
  51. disp("相关系数")
  52. xycorrcoef = corrcoef(x,y)
  53. xzcorrcoef = corrcoef(x,z)
  54. yzcorrcoef = corrcoef(y,z)
  55. corrcoef([x,y,z])
  56.  
  57.  
  58. %% 加权均值
  59. disp("加权均值")
  60. miu_w=x'*y/sum(y)
  61.  
  62. %% 加权方差
  63. disp("加权方差")
  64. xy_var=var(x,y)
  65. xy_var2=[(x-miu_w).^2]'*y/sum(y)
  66.  
  67. %% 加权标准差
  68. disp("加权标准差")
  69. xy_std=std(x,y)
  70. xy_std2=sqrt(xy_var2)

参考

均值https://ww2.mathworks.cn/help/matlab/ref/mean.html

方差https://ww2.mathworks.cn/help/matlab/ref/var.html

标准差https://ww2.mathworks.cn/help/matlab/ref/std.html

协方差https://ww2.mathworks.cn/help/matlab/ref/cov.html

相关系数https://ww2.mathworks.cn/help/matlab/ref/corrcoef.html

注：本文转载自blog.csdn.net的飞由于度的文章"https://blog.csdn.net/qq_35629563/article/details/129750644"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！