呀哈喽，我是结衣。
对于要参加程序设计比赛的人来说，算法永远都是一道绕不开的坎，你必须的去了解他才可以更好的去解决问题。非形式地说，算法就是任何良地计算过程，我们可以把算法看作是用于求良说明地计算问题地工具。那么今天我们学到的就是其中最基础的一种，双指针的应用。
在今天的这篇文章，我们将会了解到双指针的绝大多数题型，掌握了他们，那么你的双指针就算是过关了。文章的题目都是由易到难。在看完解题方法后请先自己敲出代码后再考代码部分哦。

0.双指针的介绍

常⻅的双指针有两种形式，⼀种是对撞指针，⼀种是左右指针。
对撞指针：⼀般⽤于顺序结构中，也称左右指针。
对撞指针从两端向中间移动。⼀个指针从最左端开始，另⼀个从最右端开始，然后逐渐往中间逼
近。
对撞指针的终⽌条件⼀般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循
环），也就是：
left == right（两个指针指向同⼀个位置）
left > right （两个指针错开）
快慢指针：⼜称为⻳兔赛跑算法，其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列
结构上移动。
这种⽅法对于处理环形链表或数组⾮常有⽤。
其实不单单是环形链表或者是数组，如果我们要研究的问题出现循环往复的情况时，均可考虑使⽤快
慢指针的思想。
快慢指针的实现⽅式有很多种，最常⽤的⼀种就是：
在⼀次循环中，每次让慢的指针向后移动⼀位，⽽快的指针往后移动两位，实现⼀快⼀慢。

1.移动零（easy）

题目链接：移动零
题目描述：

思路

当我们遇到这种需要将数组分为两个模块的时候，我们就可以考虑使用双指针来解决问题。

解决方法

我们用cur指针去扫描整个数组，另一个指针dest去指向cur前最后一个0的位置，每当cur指向非零元素时就交换dest和cur指向的数。

利用这个方法我们就可以把[0,dest]的元素全都转化为非0元素，[dest+1,cur-1]的元素全为0.

了解完方法后先尝试着把代码写出来吧。

代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int dest = -1,cur = 0;
        while(cur<nums.size())
        {
            if(nums[cur]!=0)
            {
                swap(nums[dest+1],nums[cur]);
                ++dest;++cur;
            }
            else
            ++cur;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

当然这题也可以用暴力写出来，不过暴力的时间复杂度就很高了为O(N^2)。所以我们还有用双指针来解决问题吧。

2.复写零（easy）

题目链接：复写零
题目描述：

思路

对数组的就地操作，尝试双指针看看。

解题方法

可题目要求我们就地修改。为了符合题意，我们要把cur和dest同时指向arr数组。如果我们重复上述的操作，在arr数组中进行就会发现，会存在数据的覆盖。

2被覆盖掉了。
那么我们要如何避免这种情况呢？既然从前向后扫描不行，那我们从后向前呢？
我们从dest和cur会停留的地方开始向前扫描。

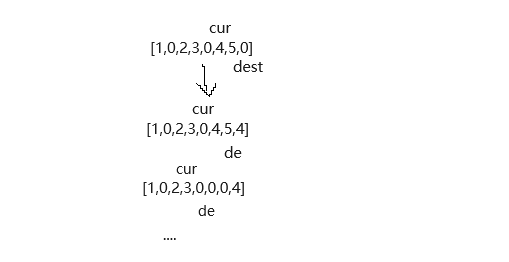
规则和前向后一样，可是后向前并不会覆盖掉数字。了解到这样步，这道题就解决了一半，为什么呢？因为我们还不知道cur和dest最后的位置。为了求到他们最后的位置，我们还要去运用一次双指针。
这次我们从前向后，cur扫描数组，如果cur指向数为0，dest+=2，不为0dest+=1.因为cur无论怎样都要加，所有我们把它放在最后加。同时，当dest指向最后一个位置时就退出循环。但是！在这种要求下会有一些特殊情况，会让dest指向数组外。当数组为[1,0,2,3,1,0,4,0]时，dest会出数组。

为此我们就需要在后续加一些判断条件，当发生这种情况时，我们直接让arr[n-1] = 0;dest-=2;cur–;

代码

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int n = arr.size();
        int dest = -1,cur = 0;
        while(cur<n)
        {
            if(arr[cur] == 0)dest+=2;
            else dest+=1;
            if(dest>=n-1)break;
            cur++;
        }
        if(dest == n)
        {
            dest--;
            arr[dest--] = 0;
            cur--;
        }
        while(cur>=0)
        {
            if(arr[cur] != 0)
            {
               
                arr[dest--] = arr[cur];
            }
            else
            {
                
                arr[dest--] = 0;
                arr[dest--] = 0;
            }
            cur--;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

3.快乐数（easy）

题目链接：快乐数
题目描述：

思路

运用鸽巢原理（抽屉原理）了解到了解到平方和最后一定会形成一个环，考虑快慢指针。

解题方法

鸽巢原理（抽屉原理）：桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。比如当我们取一个较大数，9999999999，他的各位的平方和位810.远小于他本身，同时这也是100亿内最大的各位平方和。由这个原理，我们就会知道只要循环了811个数，就一定会由重复的数出现然后形成一个环

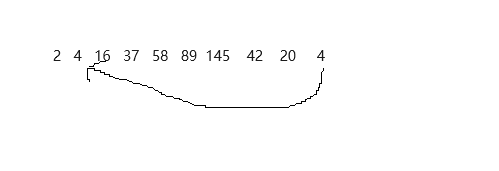
当然我们也可以把1当成循环

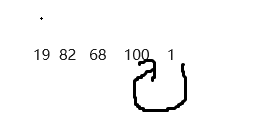
如此一来，快慢指针就发挥作用了，我们让fast指针一次走两个位置，slow指针一次走一个位置，那么可以预见的是，fast一定会先进入到环当中，当slow进入环时，fast也在环中，又因为fast速度更快，那么fast就一定会和slow相遇，我们只需要判断他们相遇的点是否为1就可以了。

复杂度

时间复杂度:$O(n)$

空间复杂度:$O(1)$

代码

class Solution {
public:
int f(int x)
{
    int sum = 0;
    while(x)
    {
        sum+=pow(x%10,2);
        x = x/10;
    }
    return sum;
}
    bool isHappy(int n) {
        int fast = n,slow = n;
        while(1)
        {
            fast = f(f(fast));
            slow = f(slow);
            if(fast == slow&&fast == 1)
            return true;
            if(fast == slow&&fast!=1)
            return false;
        }
        return false;//因为判断已经在循环中完成了，这里随便返回一个就可以了。
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

4.盛水最多的容器（medium）

题目链接：盛水最多的容器
题目描述：

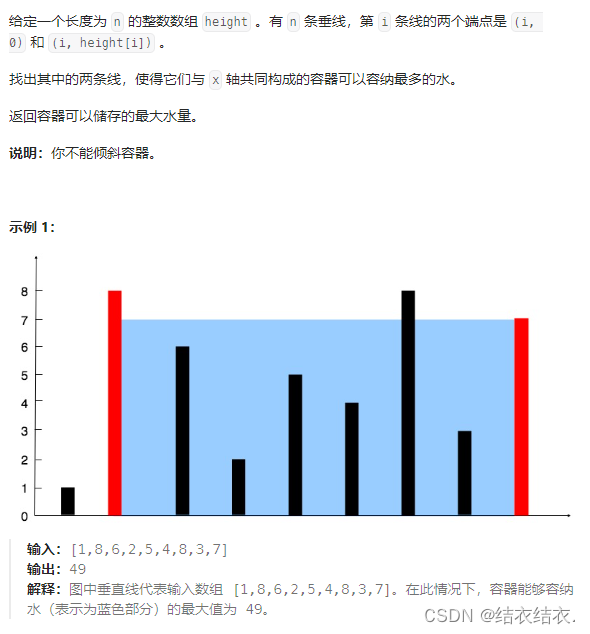
思路

因为水的面积取决于长乘宽，而长又取决于短的一边。由此我们可以得出假设先以数组的两边为长，再移动左右的长是具有一定的单调性的。

解题方法

我们以示例1为例：
我们先以两端为长，面积为1*8=8
然后我们要移动哪一个呢？如果我们移动较大的一段7
就会发现，面积绝对是变小的，因为，宽在减小，而长一定不会大于1
所以我们会移动较小的一端，直到他们相遇

左右指针，就是这题的解法。

复杂度

时间复杂度:$O(n)$

空间复杂度:$O(1)$

代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0,right = height.size()-1;
        int sum = 0;
        while(left<right)
        {
            if(height[left]<height[right])
            {
                sum = max(sum,height[left]*(right-left));
                left++;
            }
            else
            {
                sum = max(sum,height[right]*(right-left));
                right--;
            }
        }
        return sum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

5.有效的三角形个数（medium）

题目链接：有效的三角形个数
题目描述：

思路

三角形的任意两条边大于第3条边。（进阶）当已知a<=b<=c时我们只要判断a+b>c就可以了

解题方法

当我们知道进阶方法后，我们就要给数组排个序了，然后利用双指针来解决问题。
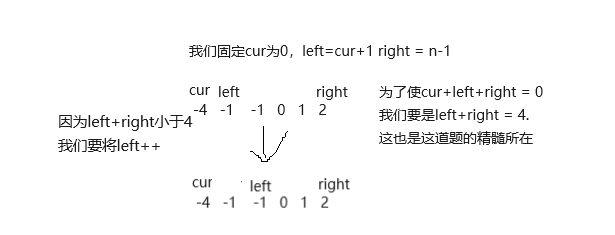
我们只需要将数组排序，然后先固定cur在数组的最大位置上。
判断left+right是否会大于cur，如果会大于cur，那么当left等于中间任何数时
都会大于cur，因为数组是递增的。我们把right–就可以了
如果left+right<=cur，我们就要left++，来找后续合适的数了。

当我们遍历完一轮后（left<=right）
我们要–cur，然后重新分配left和right
直到cur<2,就结束

复杂度

时间复杂度:$O(n^2+n\ast logn)$

空间复杂度:$O(1)$

代码

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        int n = nums.size();
        if(n<3)
        return 0;
        sort(nums.begin(),nums.end());
        int a = 0,b = n-2,c = n-1;
        int res = 0;
        while(c>=2)
        {
            a = 0;b = c-1;
            while(a<b)
            {
                if(nums[a]+nums[b]>nums[c])
                {
                    res+=b-a;
                    b--;
                }
                else a++;
            }
            c--;
        }
        return res;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

6.查找总价格为目标值的两个商品（easy）

题目链接：查找总价格为目标值的两个商品
题目描述：

思路

利用左右指针向中间扫描

解题方法

因为题目数组已经排好了序，也省去了我们排序的时间，要解决这类问题最关键的就是数组是要有序的，有序的数组可以帮我们解决很多的问题。
就那这题来说
如果le+ri大于18，那么我们肯定就要把right–啦
数组是递增的，++left只会增加le+ri。
如果le+ri小于18，我们就要把left++
道理和上面相似。
然后我们只需要重复这个过程直到找到＝tar为止

但是要注意的是因为我们一定会在循环内找到tar，但是外面也是一个返回值要不然不会让你编译成功，所以我们随便返回一个就是了

复杂度

时间复杂度:$O(n)$

空间复杂度:$O(1)$

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int n = price.size();
        int left = 0,right = n-1;
        while(left<right)
        {
            if(price[left]+price[right]>target) right--;
            else if(price[left]+price[right]<target) left++;
            else
            return {price[left],price[right]};
        }
        return {-1,-1};//但是要注意的是因为我们一定会在循环内找到tar，但是外面也是一个返回值要不然不会让你编译成功，所以我们随便返回一个就是了
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

7.三数之和（medium）

题目链接：三数之和
题目描述：

思路

由三数之和想到，固定一个数然后求数组除去这个数后的两数之和为目标值。同时注意去重，以及边界问题.

解题方法

我们先给数组排序，为了方便固定数同时也方便求两数之和。

内部求两数之和为特定值的方法和查找总价格为目标值的两个商品类似，但是我要考虑去重的问题，以及我们现在不止找以组数据，所以当我找到了一组数据时，先考虑去重的问题，

这里是会存在边界问题的，如果left跑到了数组之外怎么办，所以我们要加个left 考虑完里面后我们就要来到外面了，当里面判断完了后，我们的cur也该换位置了，我们可以往后移动一格，但是去重的问题同样要解决，所以我们可以用和上面一样的办法来解决，但是对于边界问题我们就要让cur

复杂度

时间复杂度:$O(n^2)$

空间复杂度:$O(1)$

代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        sort(nums.begin(),nums.end());
        if(nums[0]>0)
        return res;
        int cur = 0;
        int n = nums.size();
        while(cur<n&&nums[cur]<=0)
        {
            int left = cur+1,right = n-1;
            vector<int> tmp(3);
            while(left<right)
            {
                if(nums[left]+nums[right] > -nums[cur]) right--;
                else if(nums[left]+nums[right] < -nums[cur]) left++;
                else
                {
                    tmp[0] = nums[cur];
                    tmp[1] = nums[left];
                    tmp[2] = nums[right];
                    res.push_back(tmp);
                    while(left<right&&nums[left]==nums[left+1])
                    left++;
                    if(left<right)
                    left++;
                   
                }
            }
            while(cur<n-1&&nums[cur]==nums[cur+1])
            cur++;
            //if(nums[cur]<=0)*/
            cur++;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

8.四数之和（medium）

题目链接：四数之和
题目描述：

思路

思路和三数之和完全类型，我们要先把四数之和转化为三数之和，然后再转化为两数之和为目标值的问题。

解题方法

具体的解释完全可以参考三数之和，我们只需要再套一个循环来再固定一个值就可以了。

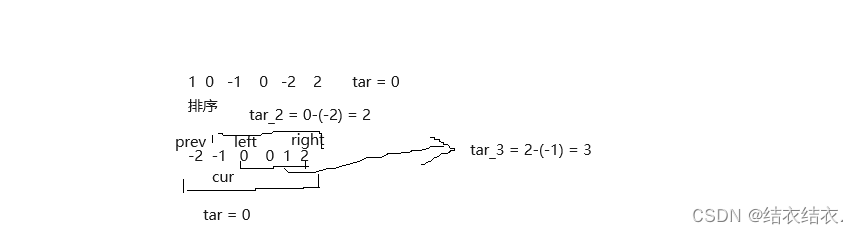
方法就是如此，这题最重要的还是边界问题，和上一题三数之和一样处理就可以了。
不过在提交之后你会遇到一个ex的例子。

没错你要考虑一下溢出的问题。

复杂度

时间复杂度:$O(n^3)$

空间复杂度: $O(1)$

代码

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> res;
        sort(nums.begin(),nums.end());
        int cur = 0;
        int n = nums.size();
        int prev = 0;
        while(prev<n)
        {
            long long target_2 = target - nums[prev];
            cur = prev+1;
        while(cur<n)
        {
            int left = cur+1,right = n-1;
            while(left<right)
            {
                long long target_3 = target_2 - nums[cur];
                if(nums[left]+nums[right] > target_3) right--;
                else if(nums[left]+nums[right] < target_3) left++;
                else
                {
                    res.push_back({nums[prev],nums[cur],nums[left],nums[right]});
                    while(left<right&&nums[left]==nums[left+1])
                    left++;
                    if(left<right)
                    left++;
                   
                }
            }
            while(cur<n-1&&nums[cur]==nums[cur+1])
            cur++;
            cur++;
        }
        while(prev<n-1&&nums[prev]==nums[prev+1])
        prev++;
        prev++;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

总结

提供这八个题目，你了解到了双指针的奥秘了吗？对于一些简单的题目，我们也许只需要定义两个指针一起向后跑就可以了，如果这两个指针在跑的过程中会出现覆盖的现象我们就要考虑从后向前来扫描数组了。当我们遇到成环的问题快慢指针来帮忙。再就是遇到要考虑单调性问题的时候，我们就可以先排序，然后再利用左右指针（对撞指针）最后就是求几个数之和为目标值之和的问题，我们同样是先排序然后在把这个问题依次降为求2个数之和为目标值的问题。

最后如果发现文章错误地方希望得到您的指正

完