前缀树算法篇：前缀信息的巧妙获取

在这里插入图片描述

那么前缀树算法是一个非常常用的算法，那么在介绍我们前缀树具体的原理以及实现上，我们先来说一下我们前缀树所应用的一个场景，那么在一个字符串的数据集合当中，那么我们查询我们某个字符串是否在这个集合当中，那么我们常规思路肯定就是会想到通过我们哈希表，哈希表的key-value模型能够很好的满足这个场景，但是如果说我们要查询这个集合的前缀信息呢，比如说我们这个集合有两个字符串“abcd”以及“abd”，那么我们假设说我们要查询以“ab”作为字符前缀的字符串在在这个集合中是否存在，那么我们知道这个集合当中的两个字符串“abcd”和“abd”都是以"ab"为字符串前缀，那么查询的结果肯定是存在，那么这一点我们哈希表就无法做到了，甚至说我还要查询这个集合中以“ab”作为字符前缀的字符串的个数有多少个，阁下该如何应对，在这个例子中，我们以“ab”为前缀的字符串的个数有两个：“abcd”以及abd“，那么接下来我将会告诉你，我一个数据结构不仅能够做到哈希表能做到的：能够查询某一个字符串是否存在于该字符串集合中，并且它还能做到哈希表不能做到的：能够查询某一个以该字符前缀的字符串是否存在，甚至还能查询以该字符前缀的字符串的数量。那么能实现这些功能的东西，就是我们今天要讲的前缀树，那么我们就来领略一下前缀树的强大以及各种骚操作

1.前缀树的原理以及实现

那么我们上文说的一通，你一定认为前缀是是一个很高大尚很复杂的一个事物，但其实它就是一个我们在熟悉不过的一个树形的数据结构，也就是一棵多叉树，只不过是一个特殊的多叉树，那么接下来我们就会讲我们这个树形数据结构怎么实现我们刚才所说的查询一个字符串以及字符前缀的，那么我们这里我们的前缀树有两种实现方式，分别是用类描述来实现，还有一种则是静态数组来实现，那么我会分别讲解这两种方式的原理以及对应的代码。

1.用类描述来实现

那么这里我们用类来实现我们的前缀树，那么我们会定义一个前缀树trie类，那么在这个类中定义出我们这棵树的节点的类描述以及我们前缀树的相关操作的函数，比如我们的插入insert函数以及删除函数和查询search函数

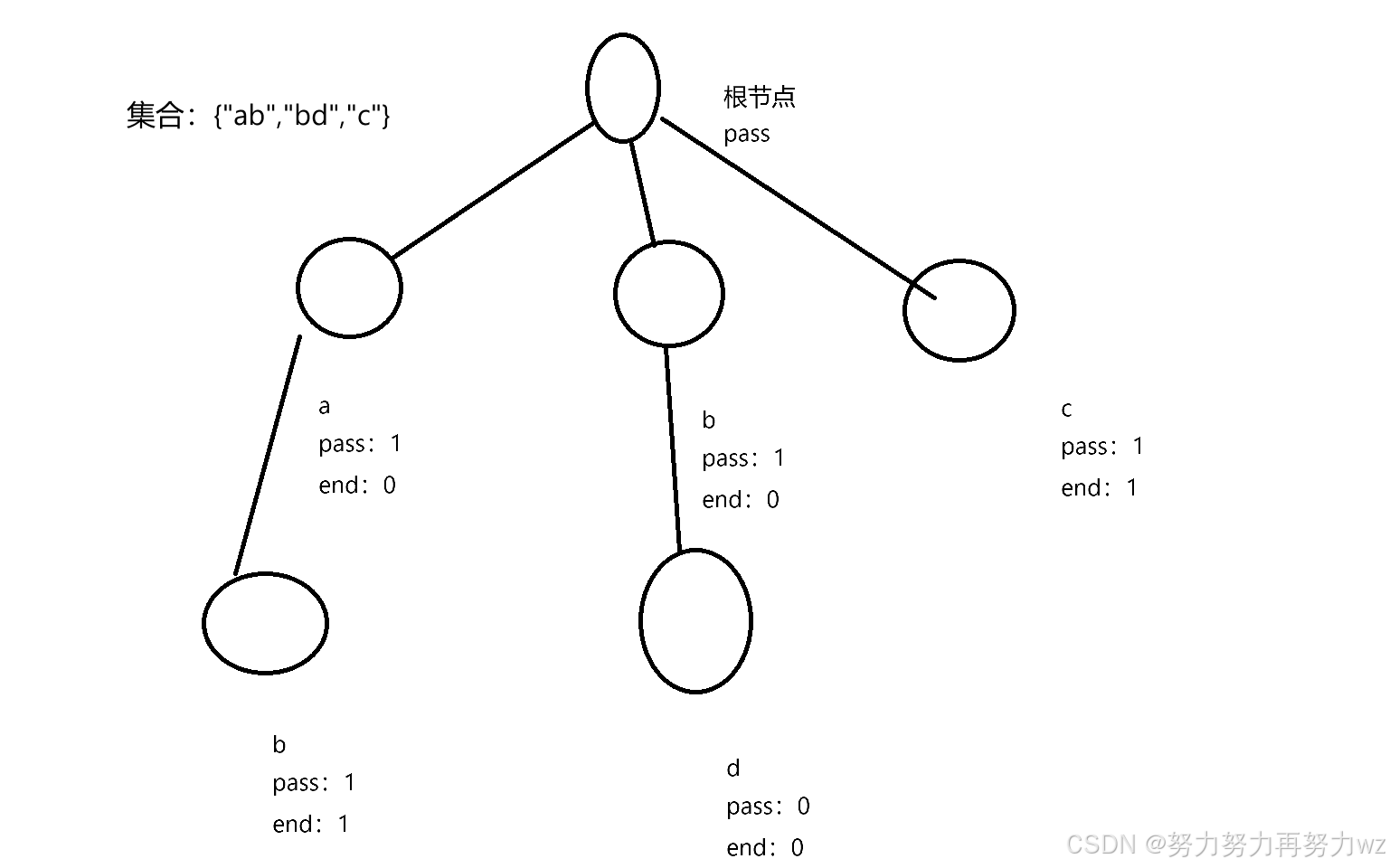
那么这里我们首先得知道我们这个前缀树的每一个节点的构造，那么我们的节点其中包含三个字段，分别是int类型的pass和end以及指针数组，那么每一个节点代表着一个字符，那么其中具体是那种字符则是看我们该节点对应父节点的指针数组的那个下标。

class trieNode
{
public:
    int pass; // 记录该节点经过的次数
    int end;  // 记录以该节点结尾的单词数量
    vector arr; // 存储子节点的指针数组，大小为26，对应26个小写英文字母

    trieNode() // 构造函数
    {
        arr.resize(26, nullptr); // 初始化数组，将每个元素都设置为nullptr
    }
};
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
插入函数：

那么这里我用一个例子来说明，假设我们这里的字符串集合当中的字符串只由26个英文字符所组成，并且我们在这个集合中只有两个字符串比如“abcd”和“abd”，那么最开始我们初始化我们的trie类得到我们的前缀树，但是我们这个前缀树还没添加我们这个集合的字符串信息，那么这棵树只有根节点，那么根节点就意味着空字符串，那么我们接下来要将我们这个集合中的字符串信息给添加到我们的前缀树中，那么就需要调用我们的insert函数，那么假如我们要插入字符串“abcd”，那么我们这里的第一个字符是a,那么我们在根节点会有一个指针数组，由于我们这里的字符串只由26个字母所组成，所以我们开辟的指针数组的长度就是26，其中每一个位置就对应一个字符，那么我们可以根据字符的阿斯克码来得到字符对应的下标，比如这里我们的第一个字符是a，那么它对应的下标就是a-‘a’ ->0，也就是0下标，那么接下来我们就检查我们的指针数组下标为0的位置的元素是否是nullptr，如果为空，那么意味着我们此时还没有添加第一个字符是’a’的字符串，那么此时我们就要申请一个节点，然后将该节点的指针赋予该数组位置上，那么如果说我们这里下标为0的位置不为空，那么我们就跳转带该下标位置所指向的节点中，然后将其pass值加一，然后插入下一个字符比如字符b。

所以我们的插入函数的实现流程就是先得到该字符所对应的指针数组位置，如果该指针数组不为空，我们跳转到该指针数组所所指向的节点中，并且节点的pass值加一，那么为空的话，我们自己申请一个节点给当前指针数组的位置，然后该申请得到的节点的pass值加一，其中要注意我们每次插入一个字符串的时候，我们知道我们会先进入根节点然后往下遍历，那么我们每次进入根节点都要将根节点的pass值加一。

那么最后我们字符串到最后一个字符的时候，我们要将该最后一个字符所对应的end值给加一。

我们在实现以及理解我们的插入函数的时候，我们脑海里面一定要有一个树形图，那么我们这里的每一层代表着一个字符串长度，比如我们把根节点的位置视作第0层，那么意味着字符串长度为0，那么第一层就是字符串长度为1，那么其中的每一个节点就代表字符前缀长度为1所对应的字符，然后第一层的每一个节点在往下有着各自的分支，代表着不同字符组合得到的不同长度的字符前缀。

代码实现：

void insert(trieNode& root,string& word)
{
	root.pass++;
	trieNode* currentNode=&root;
	 for(int i=0;iarr[word[i]-'a']==nullptr)
	 	 {
	 	 	  newnode= new trieNode;
	 	 	  currentNode.arr[word[i]-'a']=&newnode;
		  }
		  currentNode=currentNode->arr[word[i]-'a'];
		  currentNode.pass++;
		  if(i==word.size()-1)
		  {
		  	currentNode->end++;
		  }
	 }
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
查询函数：

那么我们将集合中的所有字符串都已经插入到我们的前缀树中，那么我们的查询函数就是用来查询某个完整的字符串是否存在在该集合中或者某个以该字符串为前缀的字符串是否存在在该集合中，那么我们则是利用我们节点中的pass以及end值

那么我们上文知道了我们插入函数的原理，在上文例子中我们的字符串“abcd”以及“abd”都用相同的字符串前缀“ab”,那么如果拥有相同的字符前缀，那么意味着它们在这棵多叉树种从根节点开始就有相同的一个路径分支，而由于后缀不同，所以在这个相同的路径分支下会产生分叉，那么我们创建这个路径分支（比如在刚才的例子中，我们插入的abcd是一个字符串，然后根节点指针数组对应下标为0的元素为空）或者这个路径分支已经存在，我们沿途往下遍历的时候，我们都会将该路径下的每一个节点的pass值给加一，那么也就意味着我们知道要查询某个以该字符串为前缀的字符串是否存在在该集合中，那么我们就根据该前缀依次从根节点往下遍历，如果在遍历的过程中，字符前缀的某个字符节点的指针数组元素为空，比如这里我们要查询前缀ab，那么我们从根节点遍历到下面的字符啊所在的节点，但是我们要到接下来字符b所在的节点，但是我们这里a节点的指针数组下标为1的位置如果为空，那么说明我们没有以前缀ab的字符串存在，根据我们上文的插入，我们这里如果有的话，那么我们一定会申请空间。

那么如果我们要查询前缀ab出现的次数，那么我们就找到这个前缀最后一个字符所在的节点的pass值则可以得到次数

那么同理我们查询一个完成的字符串比如abd是否存在，那么我们还是会遍历我们的前缀树，然后从根节点往下遍历到我们d节点，那么我们这里有一个误区，不要以为我们这里我们d有对应的节点存在，那么我们就认为我们完成字符串abd就存在，这里假设我们以前缀abd的字符串比如abdc，那么在插入abdc的过程中，我们会创建abd这个节点，所以这里abd整个完成字符串是否存在，那么不仅要满足我们这里d节点存在并且它对应的end值不为0，那么不为0，意味着我们从根节点到该节点沿途所组成的一个字符串是在集合中完整存在的。

代码实现：

查询完整字符串：

bool searchfullstring(trieNode& root,string& word)
{
	trieNode* currentNode=&root;
	 for(int i=0;iarr[word[i]-'a']==nullptr)
	 	{
	 	        return false;	
		 }else
		 {
		 	if(i!=word.size()-1)
		 	currentNode=currentNode->arr[word[i]-'a'];
		 	else
		 	{
		 		 if(currentNode->end==0)
		 		 {
		 		 	return false;
				  }
			 }
		 }
		 
	 }
	 return true;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24

查询字符前缀：

bool searchprestring(trieNode& root,string& word)
{
	trieNode* currentNode=&root;
	 for(int i=0;iarr[word[i]-'a']==nullptr)
	 	{
	 	        return false;	
		 }
		 	currentNode=currentNode->arr[word[i]-'a'];
	 }
	 return true;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
删除函数：

那么我们删除函数的作用就是我们比如在这个集合中某个字符串被移除了，那么我们要从前缀树中删除它之前的插入信息，那么这里我们删除函数的思路就是依次遍历这棵树中从根节点开始往下，然后依次删除沿途各个节点的pass值，如果某个节点的pass值都已经为空了，那么该字符前缀都不存在了，那么该节点所连接的表示该前缀之后的后缀肯定也不存在，我们直接删除包括该节点以及相连的整个分支，那么如果我们能到达最后一个字符，那么我们在删除这个字符的end值。

代码实现：

void deletestring(trieNode& root,string& word)
{
	 trieNode* currentNode=&root;
	 bool res=searchfullstring(root,word);
	 if(res)
	 {
	 	root.pass--;
	 for(int i=0;iarr[word[i]-'a'];
	 	   if(i==word.size()-1)
	 	   {
	 	   	current->end--;
			}
	 	   if(--current->pass==0)
	 	   {
	 	   	delete currentNode;
	 	   	  return;
			}
	 }
}
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22

2.用静态数组来实现

那么我们静态数组的实现方式则是我们比赛时候推荐使用的一种实现方式，那么我们这里相当于用一个二维数组来模拟实现我们树的一个逻辑结构，那么我们这里使用静态数组的前提是由于是静态的，那么意味着空间是不可以扩容的，那么就要求我们对我们这个字符串的数据集合的字符串数量以及字符种类有一个估计，然后开辟足够大的一个静态数组空间。

那么还是通过一个例子来理解，那么这里我们假设我们的字符串集合的字符串是由a,b,c三种字母所组成，那么我们这里我们二维数组就要开辟三列，那么每列就对应一个字符，那么其中每行就对应一个节点，那么假设我们要插入字符串"abc"，那么我们数组的第一行就是类似于我们的树形结构的根节点，那么此时我们插入字符串第一个字符a，那么我们确定字符a所对应的列下表，比如是a-‘a’,也就是0下标，那么我们此时通过编号来模拟我们树形结构节点的指针，因为我们这里是数组，那么数组是可以通过列下表来随机访问的，所以相当于我们原来树中节点的指针在这里静态数组中就变成了行下表，那么我们编号从1分配，那么我们的第一个字符对应编号就是1，那么每行就代表一个节点，那么我们就在第0行的第零列给设置为编号1，那么我们接下来跳转到第一行，然后插入我们的第二个字符b，那么此时我们的编号就来到了2，那么我们字符b就是在第二行，那么我们字符a在第一行的第一列的值就设置为2，因为字符b对应第二列，那么我们在跳转到第二行同样的流程，为字符c分配编号三，然后第二行第而列设置为我们的编号3。

然后我们的end以及pass都分别用一维数组来表示，那么我们一维数组的下标就对应二维数组的行好也就是对应各个节点的pass以及end值，那么在此过程中我们沿途遍历的时候，还是要将每一个遍历的节点的pass值加一，最后一个字符的end值加一

#include
#include
using namespace std;
int N=10000;
int m=3;
int main()
{
	vector> arr(N,vector(m));//定义二维的静态数组
	vector pass(N);
	vector end(N);
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11

插入函数代码：

void insert(vector>& num,vector& pass,vector& end,string& word)
{
	  pass[0]++;
	  int cnt=1;
	  for(int i=0;i
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
查询函数：

那么查询函数的思路很我们用类描述的思路一样，比如查询abc，那么我们从根节点也就是第0行开始，看第0行的第0列的值是否为0，为0，那么说明以该字符前缀的字符不存在，如果是非0，比如是1，那么我们就跳转到第一行，然后同样的思路知道跳转到最后一个字符所在的行，在查询对应的end值即可

代码：

查询整个字符串：

bool searchfullstring(vector>& num,vector& pass,vector& end,string& word)
{
	int cnt=0;
	  for(int i=0;i
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20

查询字符前缀：

bool searchprestring(vector>& num,vector& pass,vector& end,string& word)
{
	int cnt=0;
	  for(int i=0;i
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
删除函数：

那么删除函数则是按照上面的遍历，我们将依次遍历的节点的pass值减减，那么这里我们由于采取静态数组的方式实现，那么我们一旦在中间遍历的过程中发现某个字符的pass减完之后已经为0了，那么我们就不用往后遍历了，那么相当于后面所连接的节点就逻辑的被删除了，就好比我们事先一个顺序表，那么我们顺序表置空，其实我们不用该顺序表的空间删除，我们直接将size设置为0，就逻辑上认为该表为空表了。

代码部分：

void deletestring(vector>&num,vector& pass,vector& end,string& word)
{
	 bool res=searchfullstring(num,pass,end,word);
	 if(res)
	 {
	 	int cnt=0;
	 	pass[0]--;
	 	for(int i=0;i
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20

那么我们静态数组的视实现方式就是模拟我们的树形结构，那么我们对于原本的树形结构中从根节点到底部的各个节点在静态数组中相当于将这个树的每个节点拆开离散存放在各个不同的行，但是彼此还是记录了子节点的行号来连接。我们在写前缀树的各种比如插入以及查询函数的时候，脑海里一定要有一个树形结构的图

在这里插入图片描述

2.应用

那么了解我们前缀树的原理，那么这里我们就来通过两个题来应用一下我们的前缀树的思想，那么这两个题我都是通过静态数组的方式来实现。

题目一：匹配

题目：我们现在有两组集合a和b，那么其中这两组集合中各自含有不同的序列，那么这里我们对于每一个序列arr来说，它都有一个差值序列，其中的每一个差值是arr[i]-arr[j] (i>j)，其中arr1序列的差值序列如果和arr2序列的差值序列一样，那么我们就说两个序列是匹配的，那么返回我们b中每个序列能够匹配a的序列的数量.

例:[1,2,4,2]的差值序列是->[1,2,-2]

​ [1,3,5,3]的差值序列是->[1,2,-2]

那么两个序列的差值序列是一样的，那么我们就说这两个序列是匹配的

题目思路：那么这里我们可以首先遍历a和b两组集合当中的序列，得到各自的一个差值序列，那么这里我们可以利用我们的前缀树，将我们的a组集合中的每一个差值转换为字符串，然后将a组的每一个差值序列得到的字符串给插入到我们的前缀树中去，然后我们的b组就是查询它所对应的差值序列是否在这个前缀树中，那么如果有根据end信息来得到答案.

但是这个题我们得进行分一个特殊的一个处理，因为我们知道我们的差值的范围可以很大，我们的一个序列相邻的两个数的差值可以是10000，甚至更大，那么我们如果用静态数组实现的话，那么我们如果是以差值来作为节点来建立一棵前缀树的话，我们从差值序列的第一个数按照差值来分叉，那么我们这个静态数组得开辟多大的空间才能表示出所有的差值，那么差值假设达到一亿，那么我们静态数组要开辟一亿列吗，所以这里我们可以将我们的字符串这样转换，我们对每一个差值我们再后面添加一个#号表示结尾，那么比如差值序列[100,78,5],按照刚才的思路预处理一下我们的差值序列则是[100#78#5#],那么我们将这个字符串给"100#78#5"给插入进前缀树中，那么我们到时候遍历我们的前缀树的时候，我们就看是否存在有字符串"100#78#5#"在前缀树当中。

那么我们这里在静态数组实现的时候，我们就只需要准备12列，也就是0到9这十个数字以及#字符和负号总共12个，但是其中我们要注意我们的映射，我们0到9对应下标0到9的列，而我们的#对应第11列，负号对应第12列，然后就套我们上文的前缀树的各种模版即可

代码实现：

class soulution
｛ public：
	int searchnum(string& word,vector>& arr,vector&pass,vector& end)
	{
		int cnt=0;
		  for(int i=0;i>& arr,vector& pass,vector& end)
	{
		pass[0]++;
		int cnt=0;
		for(int i=0;i& a,vector> arr,vector& pass,vector& end)
	{
		 for(int i=0;i>& a,vector>& b,vector& ans)
	 {
	 	 vector ch1(a.size());
	 	 vectorch2(b.size());
	 	 for(int i=0;i> arr(10000,vector(12));
		  vector pass(10000);
		  vector end(10000)
		  build(ch1,arr,pass,end);
		  ans.resize(b.size());
		  for(int i=0;i
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110

题目二：求最大异或和

题目：现在我们有一个非负数序列，那么我们要求这个非负数序列中任意两个数的异或和的最大值，注意异或的两个数可以都是同一个位置。

题目思路：那么这道题的暴力方法就是写两个for循环来依次遍历，那么时间复杂度就是o(n^2)，这个肯定不是最优秀的解法。

那么我们知道异或运算的本质就是无进位相加，那么两个数进行异或运算本质就是两个数在进行无进位相加的加法运算，那么对于一个数来说，我们希望它异或的另一个数得到更大的异或和，那么策略就是这个数的最高位的位置如果是0，那么我们希望异或的对应的二进制位为1，那么同理最高位位置的二进制位为1，那么我们希望异或的该位置为0，然后我们再依次处理下一位次高位的信息，那么这里我们就可以准备一个前缀树，将我们的每一个数的二进制序列添加进前缀树当中，那么我们对于每一个数，我们分别得到它能够得到的最大异或和，然后在综合所有位置上的最大异或和得到答案，那么我们有了前缀树，那么我们就从最高位开始，然后根据高位如果是0，那么我们看有没有前缀为1的数存在，如果为1，那么我们通过前缀树查看有没有前缀为0的数存在。

那么假设我们需要的二进制位是1，但是我们序列中没有该位置为1的二进制位，那么我们就只能走0的那一个分支，反之同理。

这个题我们还可以进行一个优化，也就是我们不用把所有的二进制位给插入进前缀树，那么我们找到这个序列中最大的那个数，那么我们所有序列二进制位中最左侧的1肯定不会超过我们最大数的最左侧的1，那么意味着我们最大数二进制序列最左侧的1的前导0，那么我们其他数肯定也是有这个前导0为开头，那么对于每个二进制序列共有的前导0，那么我们不用添加进前缀树当中，相当于优化了空间

代码实现：



const int MAX_BITS = 32;
const int MAX_NODES = (1 << MAX_BITS); // 2^32, 每个节点对应一个可能的二进制前缀

// Trie节点，使用静态数组表示
struct TrieNode {
    int children[2]; // 使用索引0和1表示二进制中的0和1
};

// Trie树，使用静态数组
TrieNode trie[MAX_NODES];
int trieSize = 1; // 初始只有根节点

// 向Trie树中插入一个数
void insert(int num) {
    int currentNode = 0; // 根节点的索引
    for (int i = MAX_BITS - 1; i >= 0; --i) {
        int bit = (num >> i) & 1;
        if (trie[currentNode].children[bit] == 0) {
            trie[currentNode].children[bit] = trieSize++;
        }
        currentNode = trie[currentNode].children[bit];
    }
}

// 查找与给定数异或结果最大的数
int findMaxXOR(int num) {
    int currentNode = 0;
    int maxXOR = 0;
    for (int i = MAX_BITS - 1; i >= 0; --i) {
        int bit = (num >> i) & 1;
        int oppositeBit = 1 - bit;
        if (trie[currentNode].children[oppositeBit] != 0) {
            maxXOR |= (1 << i); // 设置当前位为1，因为我们找到了相反的位
            currentNode = trie[currentNode].children[oppositeBit];
        } else {
            currentNode = trie[currentNode].children[bit];
        }
    }
    return maxXOR;
}

// 找到数组中任意两个数异或的最大值
int findMaximumXOR(vector& nums) {
    // 初始化Trie树
    fill(begin(trie), end(trie), TrieNode{{0, 0}});
    trieSize = 1;

    // 向Trie树中插入所有数
    for (int num : nums) {
        insert(num);
    }

    // 查找每个数与Trie树中数的最大异或值，并取最大值
    int maxXOR = 0;
    for (int num : nums) {
        maxXOR = max(maxXOR, findMaxXOR(num));
    }

    return maxXOR;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64

3，结语

那么这就是我们今天关于前缀树的所有内容，那么前缀树的功能十分强大，那么知道原理以及如何应用之后，下来也要自己多加练习，因为没有哪个算法是能够看会的，那么希望本篇文章能够让你有所收获，那么我们会持续更新，希望你能够多多关注与支持！
在这里插入图片描述

注：本文转载自blog.csdn.net的努力努力再努力wz的文章"https://blog.csdn.net/2301_80260194/article/details/145599667"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！