差分可以看作是前缀和的逆运算，前缀和可以帮我们快速得到某个区间的和，而差分就是我们将原数组看作是一个前缀和数组（q[]）我们去构造一个差分数组（c[]）

一维差分

使存在如下关系：

q[i] = c[1] + c[2] + c[3] +.....+ c[i]

-> q[i] = q[i - 1] + c[i]

-> c[i] = q[i] - q[i - 1]

eg: q = {2, 3, 6, 1, 7}，下标从1开始方便讲解

按照上述规律我们可以构造出c = {2, 1, 3, -5, 6}

那么差分到底有什么用呢？

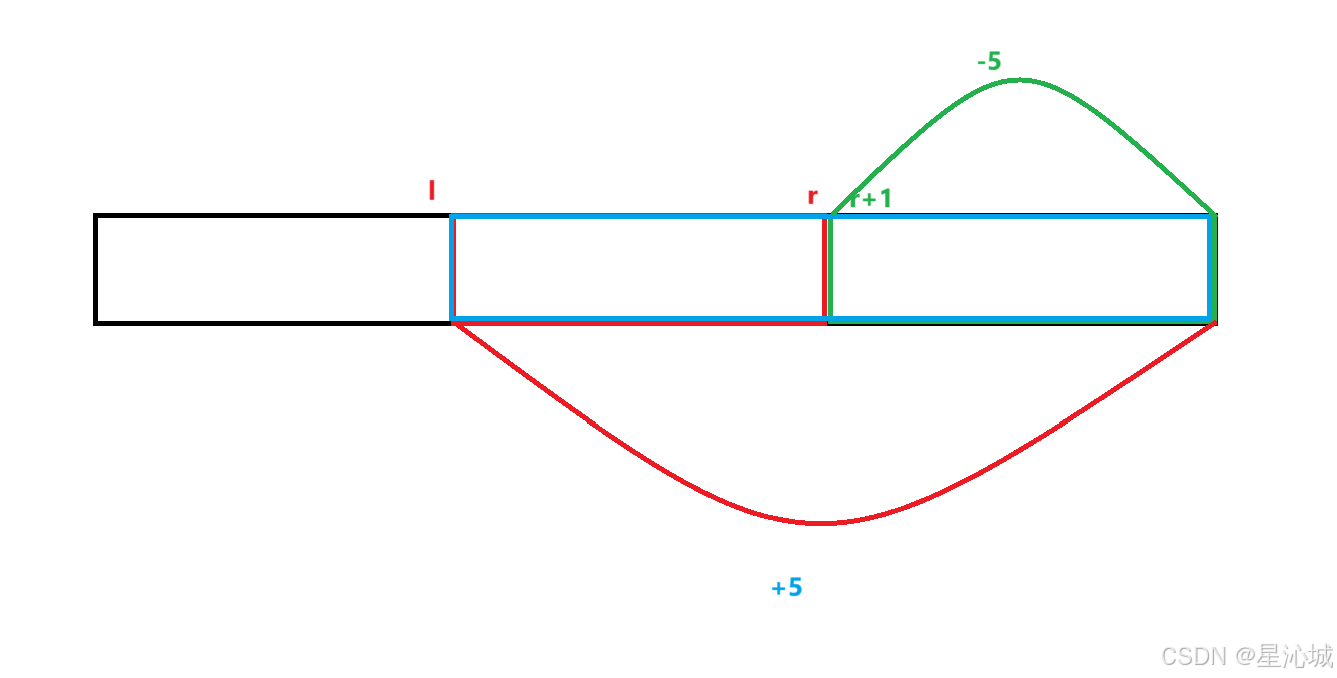
假设有这么一个场景我们现在给定一个区间[l, r]现在我们需要对原数组的[l, r]的数据都加上5，最直接的想法就是我们从l开始遍历到r然后给每个数+5，时间复杂度是O（n），如果我们现在需要执行m次如上操作就是O（n*m）这个开销不算太好。这时我们的差分就堂堂登场了，还记得差分的定义吗，原数组就是差分数组的前缀和，如果我们令c[l] + 5就是令q[l....]+5(因为l后的元素都会+c[l])，令c[r + 1] - 5就是令q[r+1....] - 5(因为r+1后的元素都会+c[r+1])，这两个一叠加就变成了q[l...r]+5了，我们只需要O（1）就能完成修改，执行m次的开销也只花费O（m），这有了极大的提升对于原来的暴力法。

代码实现：

int n, m;//n个数，m次修改
int q[n + 1], c[n + 1];
 
void change(int l, int r, int value) {
	c[l] += value;
	if(r + 1 <= n) c[r + 1] -= value;
}
 
int main() {
	for(int i = 1; i <= n; i++) c[i] = q[i] - q[i - 1];
	for(int i = 1; i <= m; i++) {
		int l, r, value;
		cin >> l >> r >> value;
		change(l, r, value);
	}
	//得到经过m次修改后的数组
	for(int i = 1; i <= n; i++) {
		q[i] = q[i - 1] + c[i];
	}
}

二维差分

二维差分的作用与一维差分是一样的，都是用来快速修改某个范围的数据，不过是从[l, r]，变成了左上顶点(x1, y1) -> 右下顶点(x2, y2)。

我们还是先来确定一下原数组和差分数组的关系，q[x] [y]等于c[1] [1]到c[x] [y]（左上顶点和右下顶点框出的矩阵）内的数据和：

q[x] [y] = c[1] [1] + ... + c[1] [y] + c[2] [1] + ...+c[2] [y] + ... + c[x] [1] +...+ c[x] [y];

我们可以画图来展现一下c数组：

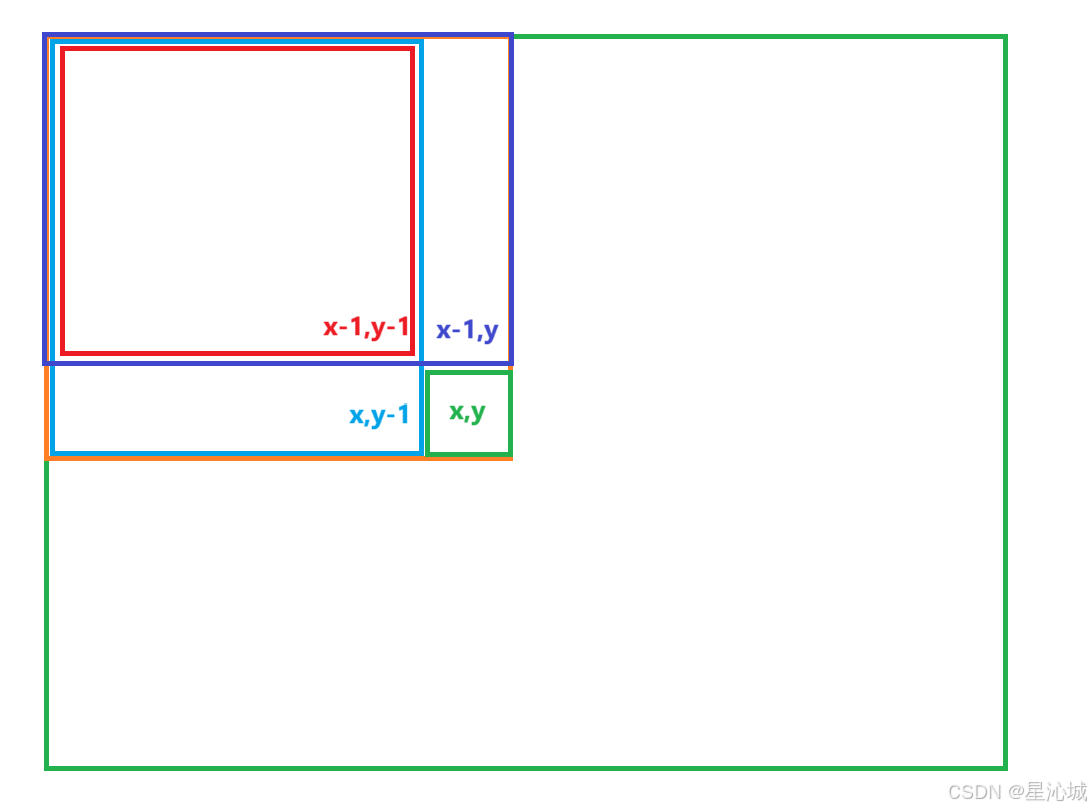
通过上述规律我们可以知道：

红色：q[x-1] [y-1]

蓝色：q[x] [y-1]

深蓝色：q[x-1] [y]

绿色：c[x] [y]

我们可以得到这样的推论：q[x] [y] = q[x - 1] [y] + q[x] [ y-1] + c[x] [y] - q[x - 1] [y - 1]，

移项后：c[x] [y] = q[x] [y] + q[x - 1] [y - 1] - q[x - 1] [y] - q[x] [y -1]

这样我们就可以通过原数组q来构造差分数组c

如果我们希望(x, y) 到 (x2, y2)范围内的数据都改变value。

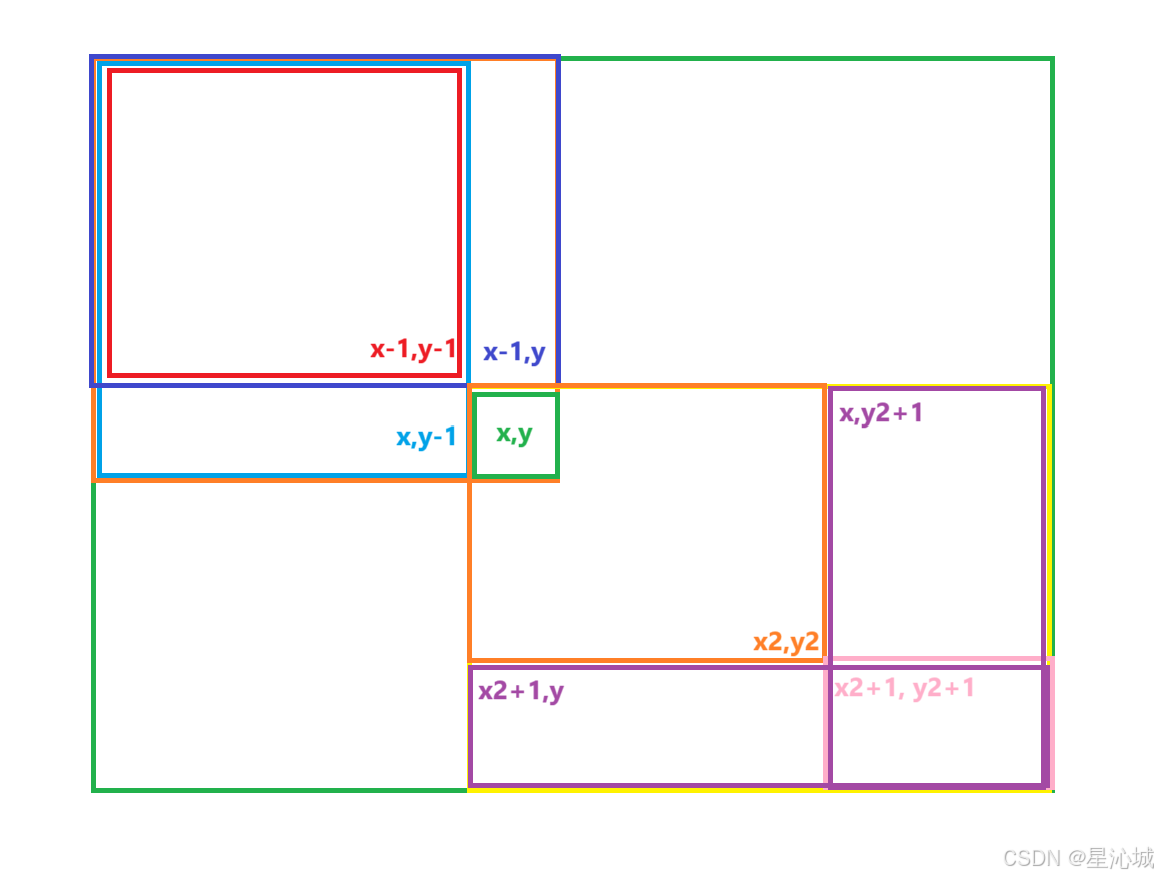
参照一维差分的规律我们可以想到就是c[x] [y] +value,会使橙色范围的q+value，我们希望紫色范围的不发生改变，所以c[x2+1] [y] - value、c[x] [y2 + 1] - value, 但这样导致粉色区域多减了一次还需要加回来c[x2+1] [y2+1] + value,这样就完成了修改

代码实现：

int q[n+1][m+1], c[n+1][m+1];//下标都还从1开始
 
void change(int x1, int y1, int x2, int y2, int value) {
	c[x1][y1] += value;
	//注意边界判断这里就不写了
	c[x2 + 1][y1] -= value;
	c[x1][y2 + 1] -= value;
	c[x2 + 1][y2 + 1] += value;
}
 
int main() {
	//num次修改
	for(int i = 1; i <= num; i++) {
		int x1, y1, x2, y2, value;
		cin >> x1 >> y1 >> x2 >> y2 >> value;
		change(x1, y1, x2, y2, value);
	}
	//得到修改后的数据
	for(int i = 1; i <= n; i++) 
		for(int j = 1; j <= m; j++) 
			q[i][j] = q[i - 1][j] + q[i][j - 1] + c[i][j] - q[i - 1][j - 1];
}