剑指offer第2版：搜索算法（二分/DFS/BFS）

        查找本质就是排除的过程，不外乎顺序查找、二分查找、哈希查找、二叉排序树查找、DFS/BFS查找  

一、p39-JZ3 找出数组中重复的数字（利用特性）

数组中重复的数字_牛客题霸_牛客网

方法1：全部排序再进行逐个扫描找重复。  时间复杂度n*logn  空间复杂度1  

  1. class Solution {
  2.   public:
  3.     int duplicate(vector<int>& nums) {
  4.         int n = nums.size();
  5.         if (n == 0) return -1;
  6.         sort(nums.begin(), nums.end());
  7.         for (int i = 1; i < n; ++i)
  8.             if (nums[i] == nums[i - 1]) return nums[i];
  9.         return -1;
  10.     }
  11. };

方法2：构造哈希——找到第一个重复的数就返回，否则正常插入    时间复杂度n  空间复杂度n

  1. class Solution {
  2.   public:
  3.     int duplicate(vector<int>& nums) {
  4.         int n = nums.size();
  5.         if (n == 0) return -1;
  6.         unordered_set<int> s;
  7.         for (int i = 0; i < n; ++i)
  8.             if (s.count(nums[i])) return nums[i];
  9.             else s.insert(nums[i]);
  10.         return -1;
  11.     }
  12. };

那么我们能否避免n的空间复杂度呢？？ 

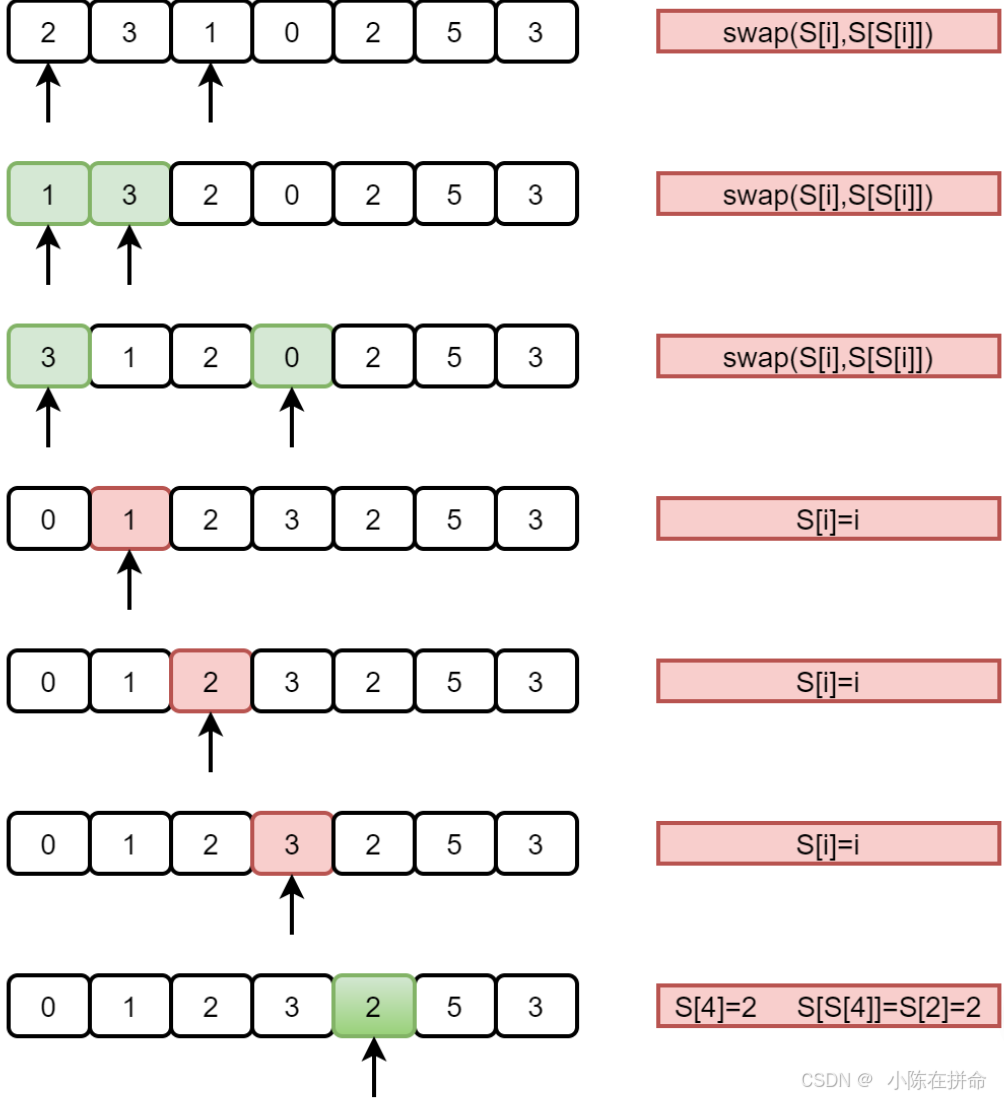
方法3：边排序边比较——我们会发现数组中的数字都在0-n-1的范围内，如果这个数组中没有重复的数字，那么当这个数组排序之后数字i将出现在下标为i的位置，同时数组中有些位置可能没有数据。    因此我们可以重拍这个数组，当扫描到下标为i的数字m的时候，首先看看m和i是否相同，如果不相同则拿他和第m个数字进行比较，如果相等说明找到了重复数字，如果不相等则把第i个数和第m个数进行交换，把m放在属于他的位置，接下来再重复这个比较、交换的过程，直到我们发现了一个重复的数字。          此时我们会发现每个数字至多比较2次就可以找到自己的位置，所以时间复杂度是n 空间复杂度1

  1. class Solution {
  2.   public:
  3.     int duplicate(vector<int>& nums) {
  4.         //重排 边排序边比较
  5.         int n = nums.size();
  6.         if (n == 0)return -1;
  7.         for (int i = 0; i < n; ++i) {
  8.             while (nums[i] != i)
  9.                 if (nums[i] == nums[nums[i]]) return nums[i];
  10.                 else swap(nums[i], nums[nums[i]]);
  11.         }
  12.         return -1;
  13.     }
  14. };

二、扩展p41-JZ3 不修改原数组基础上找出重复数（二分）

287. 寻找重复数 - 力扣（LeetCode）

     这题和上一题相似，但是区别1：不可修改原数组。区别2：该题中1-n只有n个数，但是数组中包含超过n个数，所以根据鸽巢原理，一定至少有一个数字是重复的！！

     我们把1-n的数字从中间的数字m分成两部分（概数一定出现在左半部分或者右半部分），前半部分为1->m 后面一半为m->n-1，如果1-m的数字超过了m，那么这一半钟一定包含了重复的数字，否则另一半m+1->n-1的区间里一定包含重复的数字，这样我们可以继续把包含重复数字的区间一分为2，直到找到一个重复的数字。

     按照上面的二分查找的思路，那么countrange会给调用logn次，而每次需要n的时间，所以时间复杂度为n*logn，空间复杂度1   相比于直接用哈希的做法而言，等同于用时间换空间！！但是要注意的是这个算法并不能保证找出所有重复的数字！！也不能确定该数究竟出现了几次  （所以一定要问清面试官的要求，看是要找出任意一个 还是找出所有，或者是对时间性能有什么要求，比如是空间还是时间优先） 

    这里使用左端点区间二分法

  1. class Solution {
  2. public:
  3.     int countrange(vector<int>& nums, int begin, int end) {
  4.         int count = 0;
  5.         int n = nums.size();
  6.         for (int i = 0; i < n; ++i)
  7.             if (nums[i] >= begin && nums[i] <= end)
  8.                 ++count;
  9.         return count;
  10.     }
  11.     int findDuplicate(vector<int>& nums) {
  12.         // 不修改原数组的基础上找到重复的数字
  13.         int n = nums.size();
  14.         if (n == 0)
  15.             return -1;
  16.         int left = 1, right = n - 1;
  17.         while (left < right) {
  18.             int mid = left + (right - left) / 2;
  19.             int count = countrange(nums, left, mid);
  20.             if (count > (mid - left + 1))
  21.                 right = mid; // 说明区间一定在左边
  22.             else
  23.                 left = mid + 1;
  24.         }
  25.         // 此时left==right了 我们去看看该数的数目
  26.         if (countrange(nums, left, right) > 1)
  27.             return left;
  28.         return -1;
  29.     }
  30. };

三、p44-JZ4 二维数组中的查找某数（杨氏矩阵）（利用特性）

二维数组中的查找__牛客网

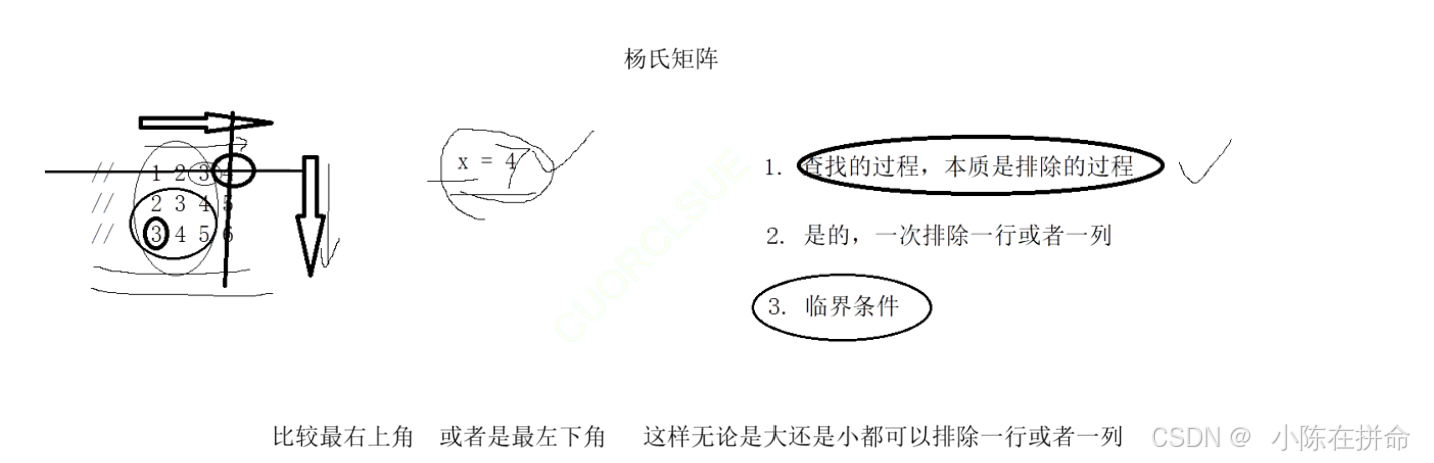
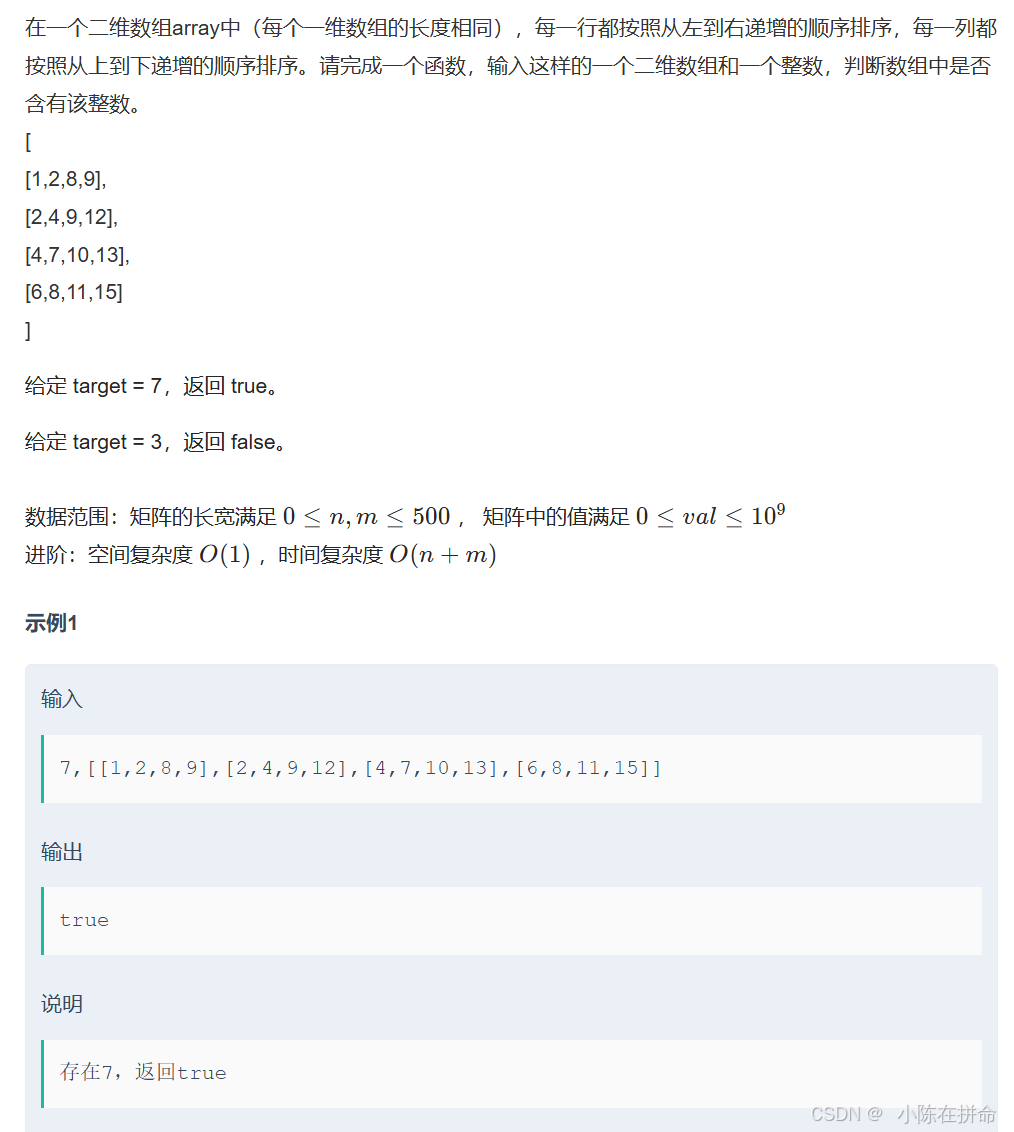       要利用他每一行和每一列都递增的特性！！先从右上角或者左下角进行比较（比如右上角，如果比右上角小，此时就可以排除列，比右上角大就可以排除行，所以无论如何都可以排除一行或者一列！！）。这样的时间复杂度就是O（m+n）

  1. class Solution {
  2.   public:
  3.     bool Find(int target, vectorint> >& array) {
  4.         int i = 0, j = array[0].size() - 1;
  5.         while (i < array.size() && j >= 0)
  6.             if (target < array[i][j]) --j;
  7.             else if (target > array[i][j]) ++i;
  8.             else return true;
  9.         return false;
  10.     }
  11. };

四、p82-JZ11 旋转数组的最小数字（二分）

旋转数组的最小数字_牛客题霸_牛客网

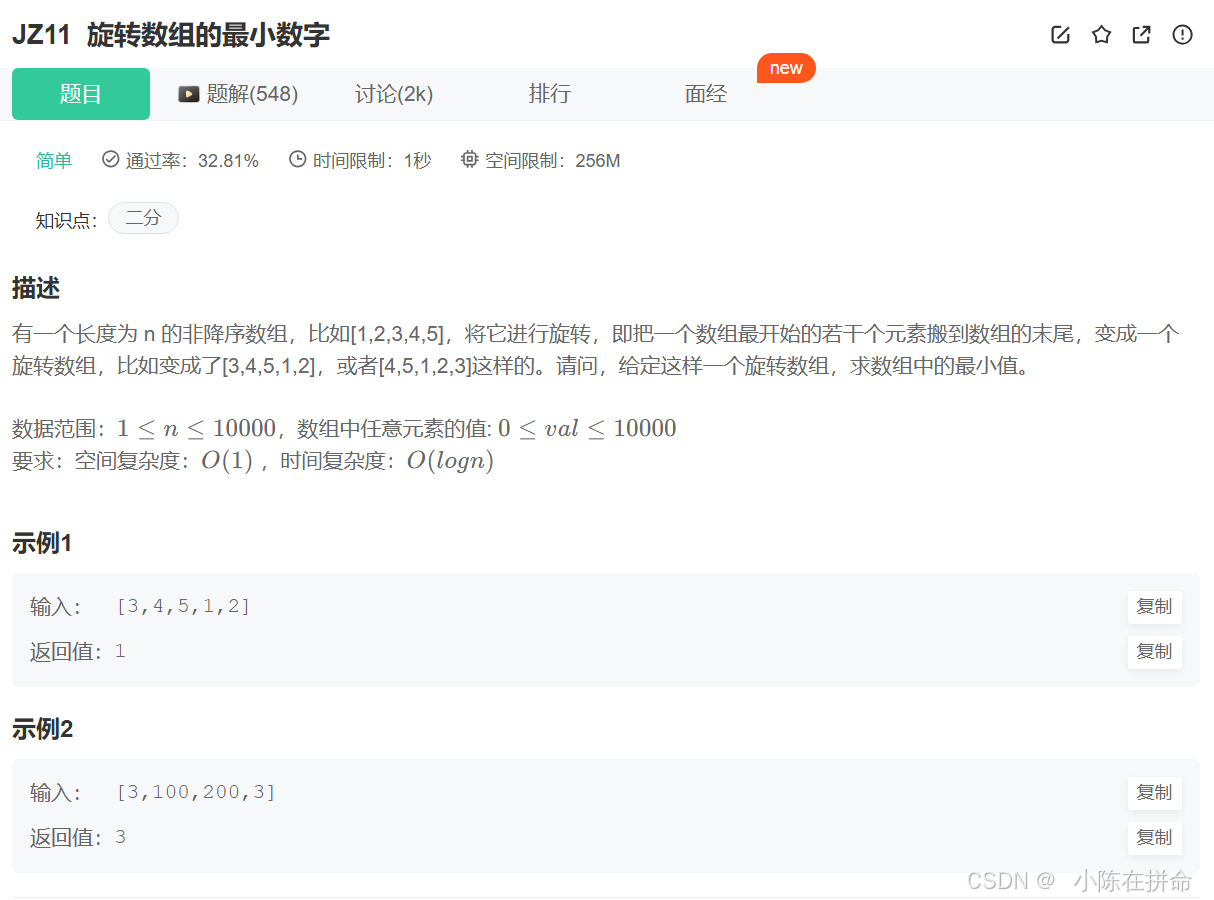        我们要注意旋转之后的数组实际上可以划分为两个排序的子数组，而前面的元素普遍大于等于后面子数组的元素！最小的元素恰好是这两个子数组的分界线！

       假如该题是严格升序的，那么图应该如下所示，此时我们会发现他具有二段性（根据某个规律可以将数组一分为二，然后再舍去其中一部分！！）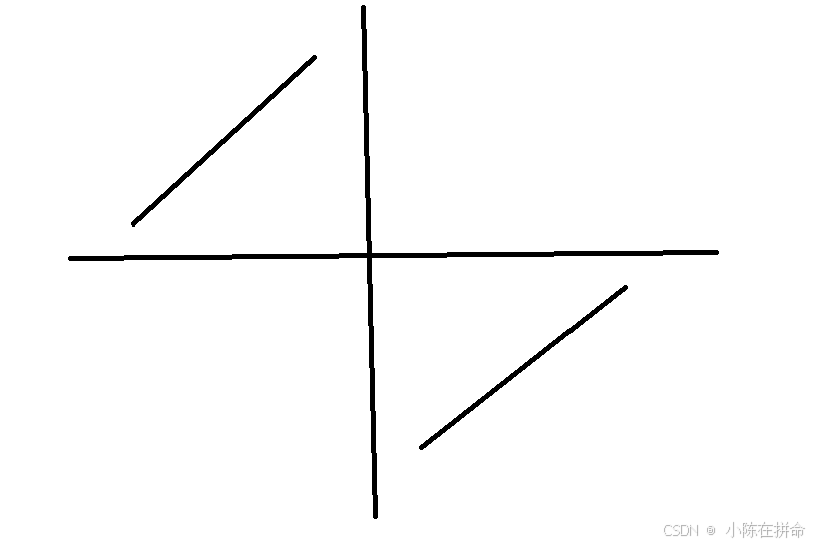

    此时我们要找的是右边区间的左端点，所以要用左端点区间二分法，此时当中间的数比左边大的时候，说明该数字在左区间，左区间要跳过去，当中间的数比右边小的时候，说明该数字在右区间，此时要右区间要跟过来。

但是有两种特殊情况：1、如果恰好旋转了n次，此时相当于原数组没有变化，那么此时直接返回第一个就可以了！！2、因为该题不是严格增，而是非递减，所以存在相等的情况，比如{1,0,1,1,1} 很有可能出现nums[mid]==left==right 此时我们就无法进行二分了！！这个时候我们只能按照笨方法进行一个个遍历了！！ 

  1. class Solution {
  2.   public:
  3.     int minNumberInRotateArray(vector<int>& nums) {
  4.         int left = 0, right = nums.size() - 1;
  5.         while (left < right) {
  6.             if (nums[left] < nums[right]) return nums[left];//情况1
  7.             int mid = left + (right - left) / 2;
  8.             if (nums[mid] > nums[left]) left = mid + 1;
  9.             else if (nums[mid] < nums[right]) right = mid;
  10.             else ++left;//此时说明nums[left]==nums[right]==nums[mid] 情况2
  11.         }
  12.         return nums[left];
  13.     }
  14. };

五、p263-JZ53 排序数组中查找数字（二分）

数字在升序数组中出现的次数_牛客题霸_牛客网

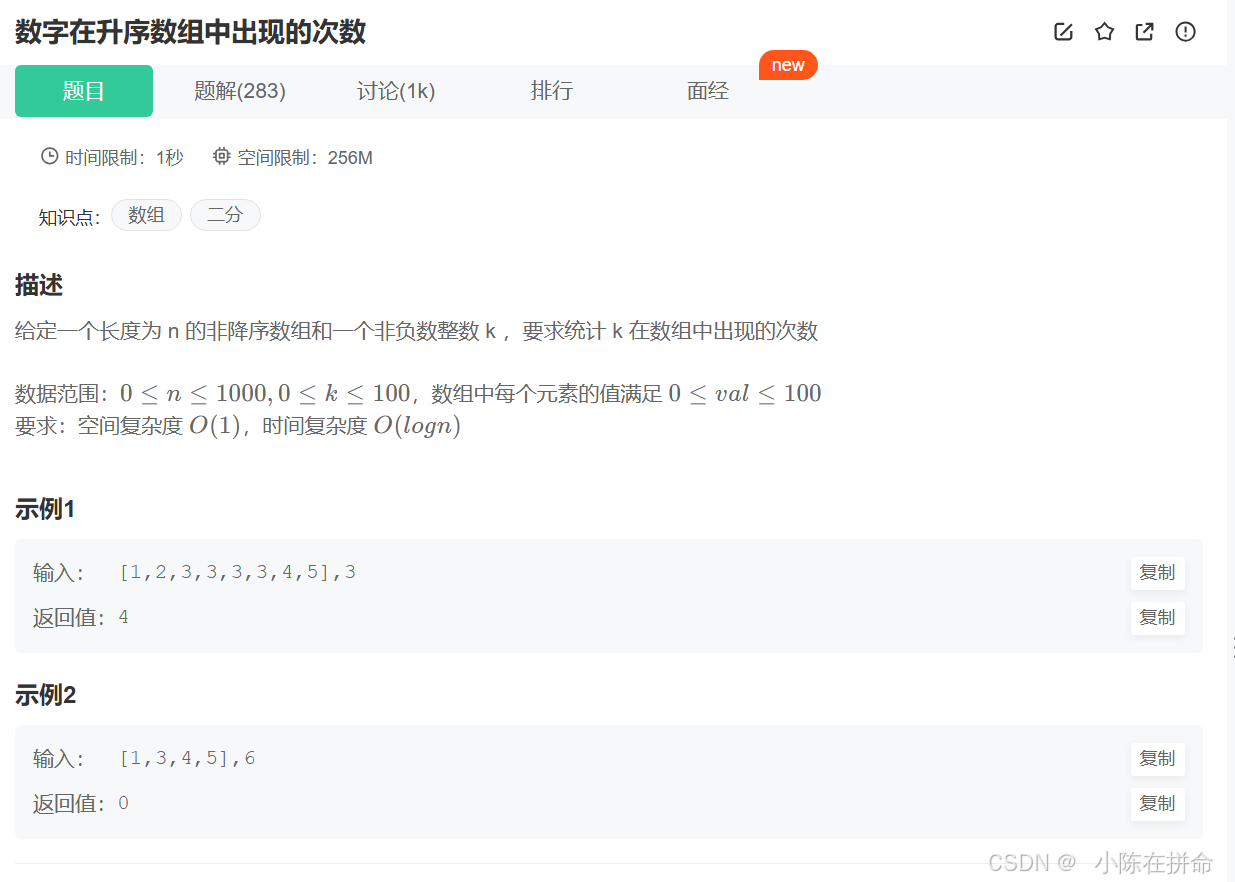
如果我们直接用朴素二分找到一个3，那么我们并不确定左边有多少右边有多少，所以我们需要尝试用左端点区间和右端点区间法找到这个数字的范围。 即找到第1个k和最后1个k。

  1. class Solution {
  2. public:
  3.     int GetNumberOfK(vector<int>& nums, int k) {
  4.       //只要找到第一个k和最后一个k  就可以统计出k在数组中出现的次数
  5.       int n=nums.size();
  6.       if(n==0) return 0;
  7.       //第一个k要用左端点区间法
  8.       int left=0,right=n-1;
  9.       while(left
  10.         int mid=left+(right-left)/2;
  11.         if(nums[mid]1;
  12.         else right=mid; //最终会落在区间的左端点
  13.       }
  14.       if(nums[left]!=k) return 0;//找不到就返回
  15.       //第二个k要用右端点区间法
  16.       int begin=0,end=n-1;
  17.       while(begin
  18.         int mid=begin+(end-begin+1)/2;
  19.         if(nums[mid]<=k) begin=mid;//最终会落在区间的右端点
  20.         else end=mid-1; 
  21.       }
  22.       return end-right+1;
  23.     }
  24. };

 六、扩展p266-JZ53 0~n-1中缺失的数字（二分）

LCR 173. 点名 - 力扣（LeetCode）

        这题有一个只管的做法就是直接用等差求和公式n（n-1）/2求出数字0~n-1所有数字之和，然后减掉整个数组的数字，就可以得到缺失的数字了，但是这种做法需要n的时间复杂度

       我们会发现该题具有二段性，即1、缺席位置之前的数和下标是一样的 2、缺席位置之后的数和下标是不一致的。所以此时我们就可以通过下标和数是否一致来进行二分查找！！

       因为我们要找的是不符合要求的第一个，所以要用左端点区间法

  1. class Solution {
  2. public:
  3.     int takeAttendance(vector<int>& nums) {
  4.         int n=nums.size();
  5.         int left=0,right=n-1;
  6.         while(left
  7.             int mid=left+(right-left)/2;
  8.             if(nums[mid]==mid) left=mid+1;//说明mid在左区间 要跳跃
  9.             else right=mid;
  10.         }
  11.         //此时right指向的就是第一个缺席的同学的位置
  12.         //但是极端情况如果缺席的正好是最后一个同学 
  13.         if(right==nums[right]) return right+1;
  14.         return right;
  15.     }
  16. };

七、p197-JZ38 字符串的排列（DFS） 

字符串的排列_牛客题霸_牛客网

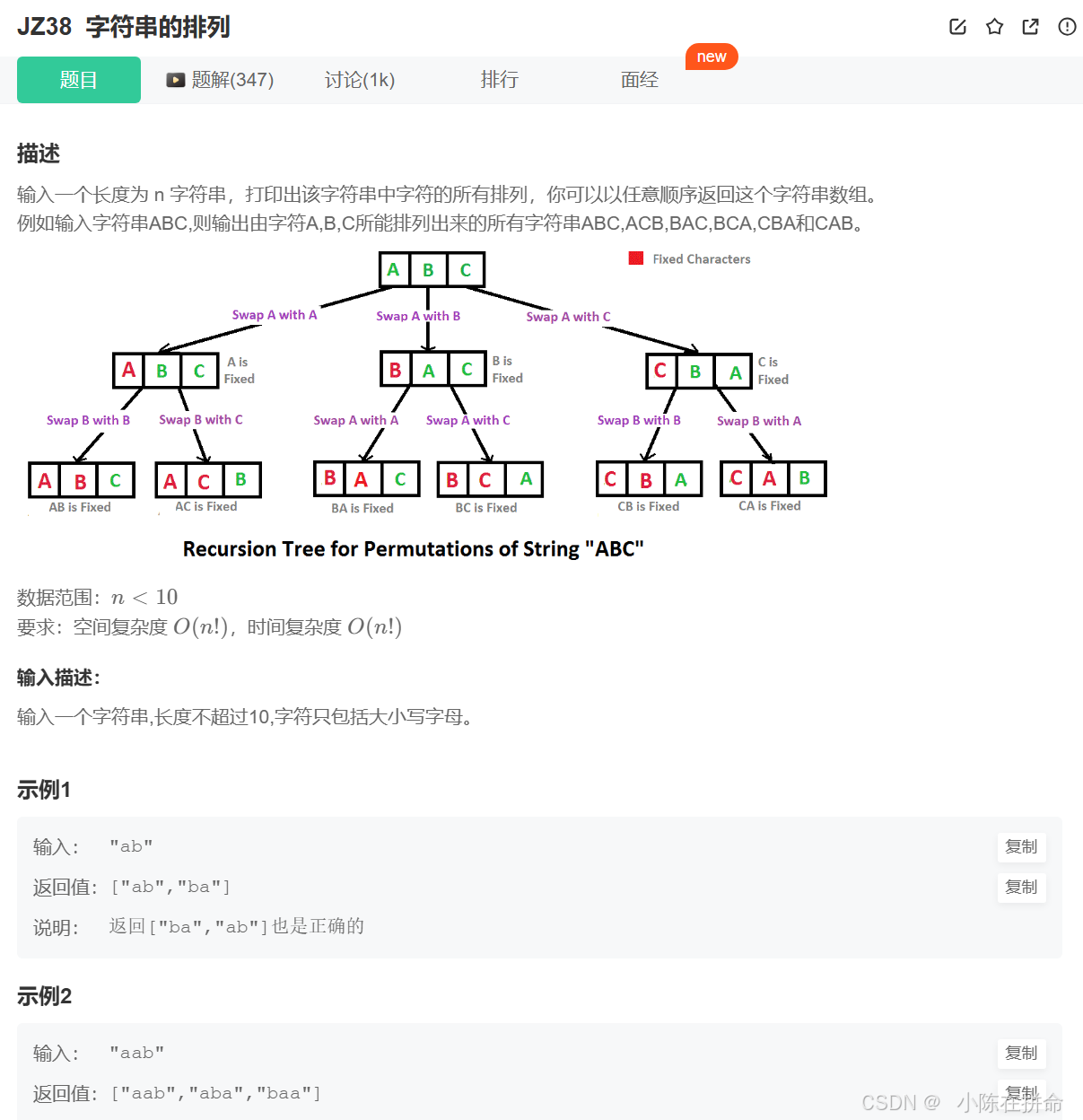
      我们可以把他拆分成小问题，根据实例2我们知道有重复的数字，所以我们可以先排序一下让相同的字母挨着一块，当前面的数跟自己相等且没有选的时候，那么自己也不能选。 

  1. class Solution {
  2.   public:
  3.     vector ret;
  4.     string path;
  5.     bool check[10] = {0};
  6.     void dfs(string s) {
  7.         if (path.size() == s.size()) {
  8.             ret.emplace_back(path);
  9.             return;
  10.         }
  11.         for (int i = 0; i < s.size(); ++i) {
  12.             if(check[i]||i>0&&s[i-1]==s[i]&&!check[i-1])  continue;//但是前面的数没选
  13.             path.push_back(s[i]);
  14.             check[i] = true;
  15.             dfs(s);
  16.             path.pop_back();
  17.             check[i] = false;
  18.  
  19.         }
  20.     }
  21.     vector Permutation(string str) {
  22.         if (str.empty()) return {};
  23.         //要去重 所以排序一下
  24.         sort(str.begin(), str.end());//保证相同的放在一起
  25.         dfs(str);
  26.         return ret;
  27.     }
  28. };

八、P89-JZ12 矩阵中的路径（DFS）

矩阵中的路径_牛客题霸_牛客网

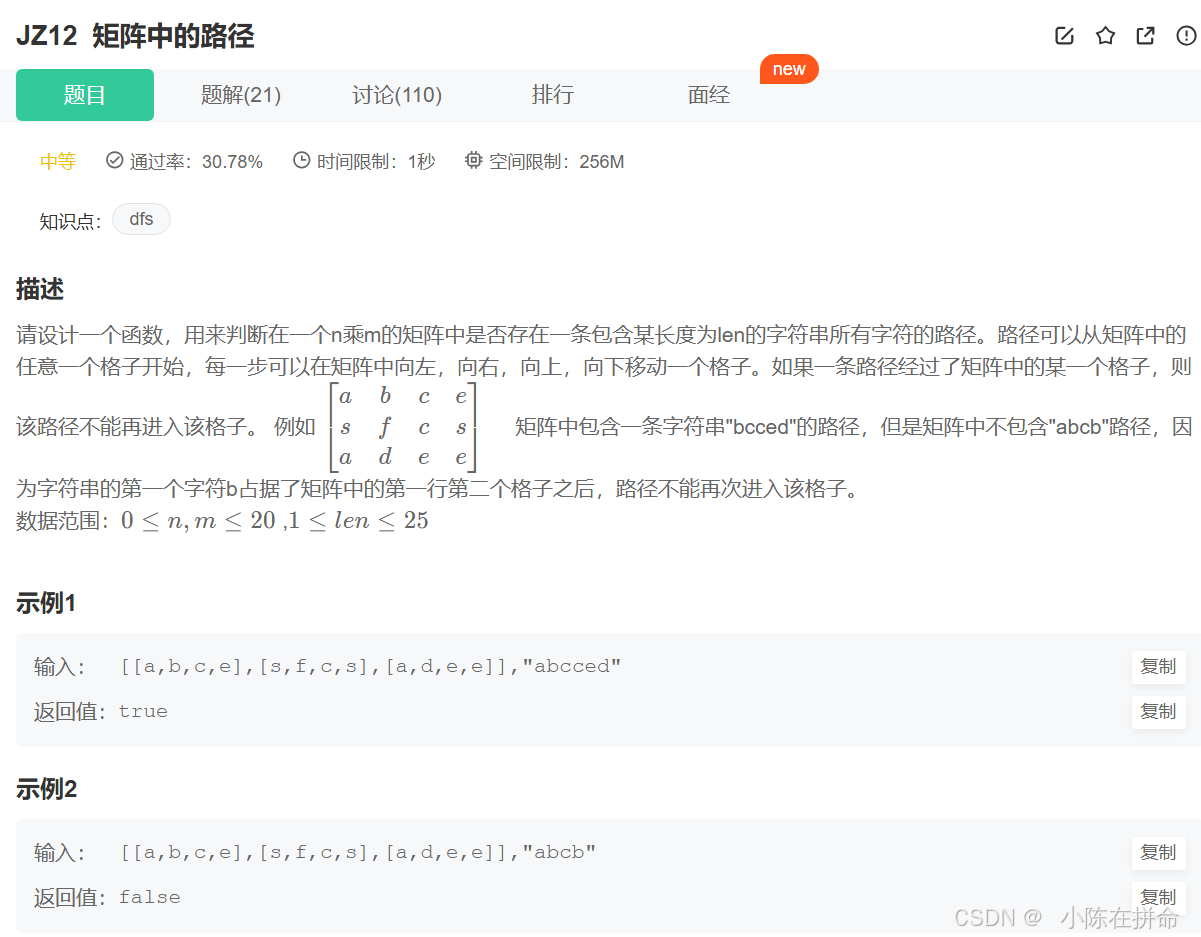
用标记数组和向量数组 

  1. class Solution {
  2.   public:
  3.     bool check[21][21] = {0}; //标记数组
  4.     int dx[4] = {0, 0, -1, 1};
  5.     int dy[4] = {1, -1, 0, 0}; //向量数组
  6.     int m,n; //长度和宽度
  7.     bool hasPath(vectorchar>>& nums, string word) {
  8.         m = nums.size();
  9.         if (m == 0) return false;
  10.         n = nums[0].size();
  11.         for (int i = 0; i < m; ++i)
  12.             for (int j = 0; j < n; ++j)
  13.                 if (nums[i][j] == word[0])
  14.                     if (dfs(nums, word, i, j, 1)) return true;
  15.         return false;
  16.     }
  17.     bool dfs(vectorchar>>& nums, string& word, int i, int j, int pos) {
  18.         if (pos == word.size()) return true;
  19.         check[i][j] = true;
  20.         for (int k = 0; k < 4; ++k) {
  21.             int x = dx[k] + i, y = dy[k] + j;
  22.             if (x >= 0 && x < m && y >= 0 && y < n && !check[x][y] &&
  23.                     word[pos] == nums[x][y])
  24.                 if (dfs(nums, word, x, y, pos + 1)) return true;
  25.         }
  26.         check[i][j] = false; //找错了就回溯
  27.         return false;
  28.     }
  29. };

 九、p92-JZ13 机器人的运动范围(DFS/BFS)

机器人的运动范围_牛客题霸_牛客网

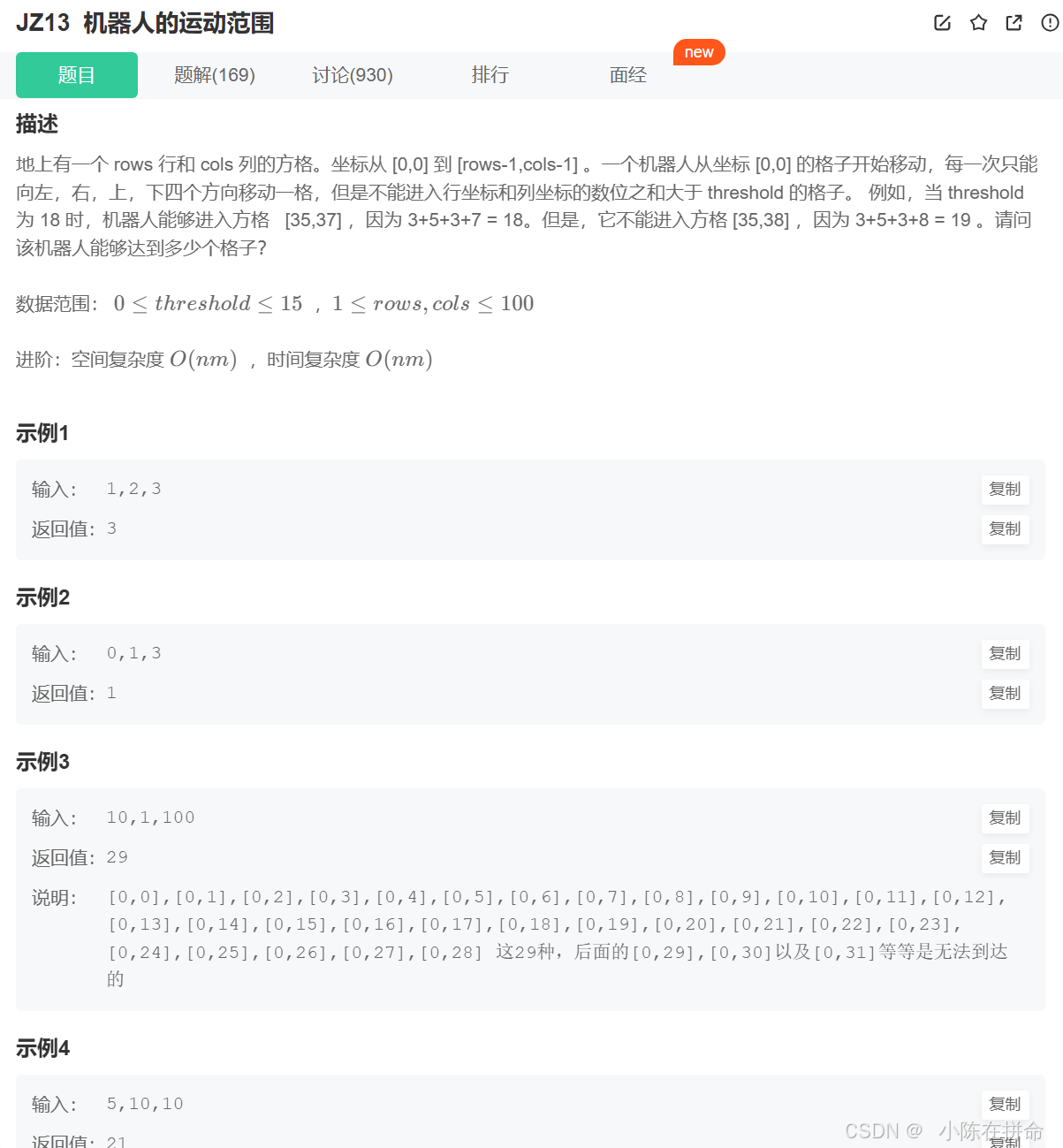
思路1：DFS 

  1. class Solution {
  2. public:
  3.     int dx[4]={-1,1,0,0};
  4.     int dy[4]={0,0,1,-1};
  5.     int vis[101][101]={0};//标记数组
  6.     int ret=0;//统计格子数
  7.     int movingCount(int threshold, int rows, int cols) {
  8.         if(threshold==0) return 1;
  9.         dfs(threshold,rows,cols,0,0);
  10.         return ret;
  11.     }
  12.      void dfs(int threshold, int m, int n,int i,int j){
  13.         if(i==m||j==n) return;
  14.         vis[i][j]=true;
  15.         ++ret;
  16.         for(int k=0;k<4;++k){
  17.             int x=dx[k]+i,y=dy[k]+j;
  18.             if(x>=0&&x=0&&ycheck(threshold,x,y))
  19.                 dfs(threshold,m,n,x,y);
  20.         }
  21.      }
  22.      bool check(int threshold,int x,int y){
  23.          int sum=0;
  24.          while(x){
  25.             sum+=x%10;
  26.             x/=10;
  27.          }
  28.          if(sum>threshold) return false;
  29.          while(y){
  30.             sum+=y%10;
  31.             y/=10;
  32.          } 
  33.          return sum<=threshold;
  34.      }
  35. };

思路2：BFS

  1. class Solution {
  2.   public:
  3.     int dx[4] = {-1, 1, 0, 0};
  4.     int dy[4] = {0, 0, 1, -1};
  5.     int vis[101][101] = {0}; //标记数组
  6.     int movingCount(int threshold, int rows, int cols) {
  7.         if (threshold == 0) return 1;
  8.         int ret = 1; //统计格子数
  9.         queueint, int>> q;
  10.         q.push({0, 0});
  11.         vis[0][0] = true;
  12.         while (!q.empty()) {
  13.             auto&[i, j] = q.front();
  14.             q.pop();
  15.             for (int k = 0; k < 4; ++k) {
  16.                 int x = dx[k] + i, y = dy[k] + j;
  17.                 if (x >= 0 && x < rows && y >= 0 && y < cols && !vis[x][y] &&
  18.                         check(threshold, x, y)) {
  19.                     q.push({x, y});
  20.                     ++ret;
  21.                     vis[x][y] = true;
  22.                 }
  23.             }
  24.         }
  25.         return ret;
  26.     }
  27.     bool check(int threshold, int x, int y) {
  28.         int sum = 0;
  29.         while (x) {
  30.             sum += x % 10;
  31.             x /= 10;
  32.         }
  33.         if (sum > threshold) return false;
  34.         while (y) {
  35.             sum += y % 10;
  36.             y /= 10;
  37.         }
  38.         return sum <= threshold;
  39.     }
  40. };

注：本文转载自blog.csdn.net的✿༺小陈在拼命༻✿的文章"https://blog.csdn.net/weixin_51142926/article/details/144746140"。版权归原作者所有，此博客不拥有其著作权，亦不承担相应法律责任。如有侵权，请联系我们删除。
复制链接
相关推荐
发表评论

评论记录：

未查询到任何数据！