前言

因疫情原因，距上次写博客已过许久

这次回看以前的书籍，发现数据预处理这块在业务中极其重要

业务中，数据的准确率对业务的影响至关重要

好的数据往往百利而无一害，相对的，不好的数据会带来无法预期的损失

管理好数据，就能管理好业务，环环相扣，生生不息

所以这次复习并巩固这块相关知识

技术之路任重而道远，负重前行，坚持到底。

数据预处理概述

数据是机器学习和数据分析的基础

1. 数据清理：主要是指将数据中缺失的值补充完整、消除噪声数据、识别或删除离群点并解决不一致性。主要达到的目标：将数据格式标准化、异常数据清理、错误纠正、重复数据的清除。
2. 数据集成：主要是将多个数据源中的数据进行整合并统一存储。
3. 数据变换:主要是指通过平滑聚集、数据概化、规范化等方式将数据转换成适用于数据挖掘的形式。
4. 数据归约：数据挖掘时往往数据量非常大，因此在少量数据上进行挖掘分析就需要很长的时间，数据归约技术主要是指对数据集进行归约或简化，不仅保持原数据的完整性并且数据归约后的结果与归约前的结果相同或几乎相同。

数据清理

异常数据处理

异常数据也称离群点，指采集的数据中，个别值的数据明显偏离其余的观测值

如测量小学五年级学生的身高数据，其中一部分数据如下：

( 1.35，1.40，1.42，1.38，1.43，1.40 )

上面这组数据符合小学五年级学生的身高情况，但是如果数据中存在下面一组数据。

( 1.35，1.40，1.42，13.8，1.43，1.40 )

其中第4个数据为 13.8，这个数据明显是不可能的，其原因或者是输入错误，或者是测量错误，因为这个数据远远偏离正常数据，因此需要对这类数据进行相应的处理。如果对这些数据不采用一定的方法消除，对结果将产生较坏的影响。

1、异常数据分析

在处理异常数据之前，首先需要对异常数据进行分析，常见的分析方法如下：

1. 使用统计量进行判断:可以对该数据计算出最大值、最小值及平均值，来检查某个数据是否超出合理的范围。例如，上面的身高数据如果远超出正常数据，那么就可以认为是异常数据。
2. 使用3σ原则: 根据正态分布的定义，距离平均值3以外的数值出现属于小概率事件，此时，异常值可以看成那些数据和平均值的偏差超过3倍标准差的值。
3. 使用箱型图判断:箱型图可以直观地表示数据分布的具体情况，如果数据值超出箱型图的上界或下界都认为是异常数据，如下图所示。

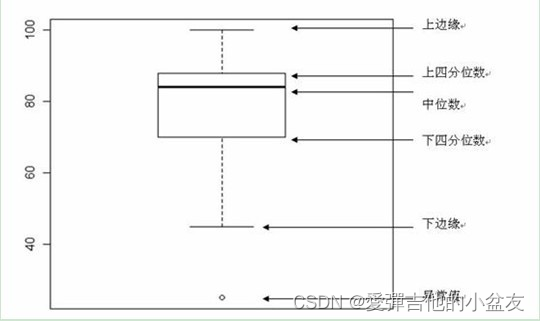
2、异常数据处理方法

当数据中存在异常数据时，应根据情况来确定是否需要对这些数据进行处理

经常传用的方法如下：

1. 删除有异常数据的记录：直接把存在的异常数据删除，不进行考虑。
2. 视为缺失值：将异常数据看成缺失值，按照缺失值的处理方法进行相应操作。
3. 平均值修正：使用前后两个观测值的平均值代替，或者使用整个数据集的平均值代替。
4. 不处理：将异常数据当成正常数据进行操作。

缺失值处理

数据缺失是指所记录的数据由于某些原因使部分数据丢失，如采集测量小学五年级学生的身高数据

其中一部分数据如下：

(1.35，1.40，1.42，***，1.43，1.40)

如上所示，第四名同学由于测量时没有到校，缺少该同学的数据。那么到统计全班同学的身高数据时，这名没有测量的同学的身高数据如何处理呢? 是不考虑这名同学的数据，还是采用一些方法取近似数据呢?

上面介绍了数据缺失的情况，产生数据缺失的原因多种多样，主要有以下几个：

1. 部分信息因为不确定的原因暂时无法获取。
2. 有些信息虽然记录了，但是由于保存不当，部分丢失。
3. 由于采集信息人员工作疏忽，漏记某些数据。

如果数据中存在缺失值，对机器学习的效果会产生一定影响，特别是丢失的数据如果非常重要，那么机器学习的效果会很差，所得到的模型参数也不准确。因此如果数据中存在缺失的情况，应采取措施进行处理。

处理缺失值的方法有很多，如忽略存在缺失数据的记录、去掉包含缺失数据的属性手工填写缺失值、使用默认值代替缺失值、使用属性平均值(中位数或众数代替缺失值使用同类样本平均值代替缺失值、预测最可能的值代替缺失值等。

其中，经常使用数据补插方法来代替缺失值，这些方法又可以细分为以下几种：

1. 最近邻补插：使用含有缺失值的样本附近的其他样本的数据替代;或者前后数据的平均值替代等。
2. 回归方法：对含有缺失值的属性，使用其他样本该属性的值建立拟合模型，然后使用该模型预测缺失值。
3. 插值法：和回归法类似，该方法使用已知数据建立合适的插值函数，缺失值使用该函数计算出近似值代替。常见的插值函数有拉格朗日插值法、牛顿插值法、分段插值法、样条插值法、Hermite 插值法等。

噪声数据处理

噪声无处不在，即使非常精密的仪器在测量时也存在或大或小的噪声。同样，噪声对学习的影响也有大有小，这取决于噪声相比真实数据的比例，也取决于学习的精度要求。

噪声数据的一般处理方法包括分箱、聚类和回归。

1. 分箱方法：把待处理的数据(某列属性值)按照一定的规则放进一些箱子(区间)中，考察每一个箱子(区间)中的数据，然后采用某种方法分别对各个箱子(区间)中的数据进行处理。在采用分箱技术时，需要确定的两个主要问题就是，如何分箱及如何对每个箱子中的数据进行平滑处理。

   分箱的方法一般有以下几种：

   1）等深分箱法也称为统一权重法，该方法将数据集按记录行数分箱，每箱具有相同的记录数，每箱记录数称为箱子的深度。这是最简单的一种分箱方法。

   2）等宽分箱法也称为统一区间法，使数据集在整个属性值的区间上平均分布，即每个箱的区间范围是一个常量，称为箱子宽度。

   3）用户自定义区间，用户可以根据需要自定义区间，当用户明确希望观察某些区间范围内的数据分布时，使用这种方法可以方便地帮助用户达到目的。

   例如，客户收入属性 income 的数据排序后的值如下（人民币元）。

   800，1000 ，200，1500，1500，1800，2000，2300，2500，2800，3000，3500，4000，4500，4800，5000

   使用分箱方法的结果如下：

   等深分箱法:设定权重（箱子深度）为4，分箱后的结果如下：

   箱 1： 800，1000，1200，1500

   箱 2：1500，1800，2000，2300

   箱 3：2500，2800，3000，3500

   箱 4：4000，4500，4800，5000

   等宽分箱法：设定区间范围（箱子宽度）为人民币 1000 元，分箱后的结果如下：

   箱 1： 800，1000，1200，1500，1500，1800

   箱 2：2000，2300，2500，2800，3000

   箱 3：3500，4000，4500

   箱 4：4800，5000

   分箱后就需要对每个箱子中的数据进行平滑处理。常见的数据平滑方法如下：

   1）按平均值平滑：对同一箱值中的数据求平均值,用平均值替代该箱子中的所有数据。

   2）按边界值平滑：用距离较小的边界值替代箱中每一个数据。

   3）按中值平滑：取箱子的中值，用来替代箱子中的所有数据。

2. 聚类方法：将物理的或抽象对象的集合分组为由类似的对象组成的多个类，然后找出并清除那些落在簇之外的值（孤立点），这些孤立点被视为噪声数据。

3. 回归方法：试图发现两个相关的变量之间的变化模式，通过使数据适合一个函数来平滑数据，即通过建立数学模型来预测下一个数值，所采用的方法一般包括线性回归和非线性回归。

除了以上的噪声处理的方法，近年来小波等技术也被引入了数据降噪。

数据集成

人们日常使用的数据来源于各种渠道，有的是连续的数据，有的是离散 数据，有的是模糊数据，有的是定性数据，有的是定量数据。数据集成就是将多文件或多数据库中的异构数据进行合并，然后存放在一个统一的数据库中进行存储。在数据的集成过程中，一般需要考虑以下问题。

1、实体识别

主要指数据源来源不同，其中的概念定义不一样。主要有以下几种情况：

1. 同名异义：数据源A的某个数据特征的名称和数据源B的某个数据特征的名称一样，但表示的内容不一样。例如，数据源A的某个数据特征的名称是ID，表示学生的学号，而数据源 B 的某个数据特征的名称也是 D，但是表示的是产品编号。
2. 异名同义：指数据 的某个数据特征的名和数 B 的某个据特的名称不一样，但表示的内容一样。例如，数据源 A 的某个数据特征的名称是 D，表示学号，数据源 B 的某个数据特征的名称 xuehao，记录的也是学生的学号。
3. 单位不统一：指不同的数据源记录的单位不一样，如统计身高，一个数据源使用米作为单位，而另一个数据源使用英尺作为单位。

2、冗余属性

是指数据中存在余，一般分以下两种情况。

1. 同一属性多次出现，如两个数据源都记录了每天的最高温度和最低温度，当数据集成时就出现两次。
2. 同一属性命名不一致而引起数据重复，如两个数据源分别要求测量每天的温度，但是特征的名称不一样，这样数据集成时也存在数据的重复。

3、数据不一致

编码使用的不一致问题和数据表示的不一致问题，如日期“2004/12/25”和“25/12/2004”表示的是相同的日期。

例如，身份证号码，旧的身份证号码是15位，新的身份证号码是18位。

数据变换

数据变换是指将数据转换或统一成适合机器学习的形式。就像人类学习一样，需要将采集的外部数据转换成可以接收的形式，如医院的老中医具有很高深的医学知识，然而他们不会使用计算机，也不擅长将他们所掌握的知识写成书籍，这就需要有专门的人员和老中医一起生活和工作，把他的经验总结成他人易于接受的书本知识，才可以使老中医的技术传承下去。同样，外部的声音信息要转换成计算机可识别的信息，首先需要进行声电转换，再转换成计算机可识别的二进制数据。

由于实际过程中采集的各种数据，形式多种多样，格式也不一致，这些都需要进行一定的数据预处理，使它们符合机器学习的算法使用。

数据变换常用方法如下：

1、使用简单的数学函数对数据进行变换

对采集的原始数据使用各种简单的数学函数进行变换，常见的函数包括平方、开方、取对数、差分运算等。

当然具体使用哪一种数学函数也取决于数据和应用的场景。例如，如果数据较大，可以取对数或开方将数据压缩变小;如果数据较小可以使用平方扩大数据。在时间序列分析中，经常使用对数变换或差分运算将非平稳序列转换为平稳序列。

2、归一化

归一化又称为数据规范化，是在机器学习中数据预处理经常使用的方法，主要用于消除数据之间的量纲影响 。这是因为数据采集过程中，不同的数据值有可能差别很大，有时甚至具有不同的量纲，如比较工资收入，有的人每月工资上万元，有的人每月工资才几百元如果这些数据不进行调整有可能影响数据分析的结果，因此需要进行归一化处理，将数据落入一个有限的范围，常见的归一化将数据调整到[0,1]或[-1,1]范围内。

1、最小一最大归一化

最小一最大归一化也称为离差标准化，是对原始数据进行线性变换，使其值映射到[0.11之间

转换函数如下：

$$X=\frac{X-X\min }{X\max -X\min }$$

式中，X为需要归一化的数据;Xm为全体样本数据的最大值;为全体样本数据的最小值。

这种方法的缺陷就是当有新数据加入时，可能导致和的变化，需要重新定义。

2、Z-score 标准化方法

Z-score标准化方法也称为零-均值规范化方法这种方法使用原始数据的均值(Mean)和标准差( Standard Deviation)对数据实施标准化。经过处理的数据符合标准正态分布即均值为0，标准差为 1，转化函数为:

$$X=\frac{X-\mu }{\sigma }$$

式中，X是全体样本数据的均值;从是全体样本数据的标准差。

Z-score 标准化归一化方式要求原始数据的分布可以近似为高斯分布，否则，归一化的效果会变得很糟糕。

3、小数定标规范化

小数定标规范化通过移动数据的小数点位置进行规范化 。

转化公式为：

$$X=\frac{X}{10^k}$$

3、连续属性离散化

数据离散化本质上是将连续的属性空间划分为若干个区间，最后用不同的符号或整数值代表每个子区间中的数据。离散化涉及两个子任务:确定分类及将连续属性值映射到这些分类值。

在机器学习中，经常使用的离散化方法如下：

1、等宽法

根据需要指定将数据划分为具有相同宽度的区间，区间数据事先制定,然后将数据按照其值分配到不同区间中，每个区间用一个数据值表示。

2、等频法

这种方法也是需要实现把数据分为若千个区间，然后将数据按照其值分配到不同区间中，但是和等宽法不同的是，每个区间的数据个数是相等的。

3、基于聚类分析的方法

这种方法典型的算法是K-means算法，K-means算法首先从数据集中随机找出K个数据作为K个聚类的中心；其次根据其他数据相对于这些中心的欧式距离，对所有的对象聚类，如果数据 x 距某个中心最近，则将 x 划归该中心所代表的聚类；最后重新计算各区间的中心，并利用新的中心重新聚类所有样本。逐步循环，直到所有区间的中心不再随算法循环而改变。

以上方法在机器学习算法中经常会使用到，近年来，基于熵的离散化方法，各种基于小波变换的特征提取方法，自上而下的卡方分裂算法等也被不同的学者采用。

前面介绍了多种数据变换的方法，但是大家要注意，具体某个机器学习所使用的数据使用哪种预处理方法更为适合，都需要经过实验进行验证。

数据规约

数据归约是指在尽可能保持数据原貌的前提下，最大限度地精简数据量原数据可以用得到数据集的归约表示，它接近保持原数据的完整性，但数据量比原数据小得多，与非归约数据相比，在归约的数据上进行挖掘，所需的时间和内存资源更少，挖掘将更有效，并产生相同或几乎相同的分析结果。

1、常用维归约、数值归约等方法实现

维归约也称为特征规约，是指通过减少属性特征的方式压缩数据量，通过移除不相关的属性，可以提高模型效率。维归约的方法很多。例如，AIC准则可以通过选择最优模型来选择属性

LASSO 通过一定约束条件选择变量

分类树、随机森林通过对分类效果的影响大小筛选属性

小波变换、主成分分析通过把原数据变换或投影到较小的空间来降低维数。

2、数值归约

数值归约也称为样本规约，样本归约就是从数据集中选出一个有代表性的样本的子集。子集大小的确定要考虑计算成本、存储要求、估计量的精度及其他一些与算法和数据特性有关的因素。例如，参数方法中使用模型估计数据，就可以只存放模型参数代替存放实际数据，如回归模型和对数线性模型都可以用来进行参数化数据归约。对于非参数方法可以使用直方图、聚类、抽样和数据立方体聚集为方法。

结语

能看到这儿，您已经很不错了，我都写困啦

给你一个大大的赞

本篇内容参考自《Python3数据分析和机器学习实战》一书。