人工智能|Bid Landscape论文阅读笔记

概述

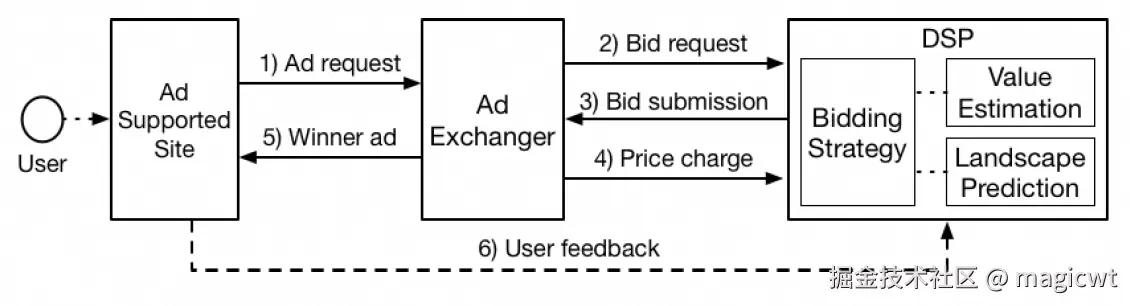
图1 程序化广告投放流程和涉及方

笔者梳理的《基于PID控制器的自动出价》介绍了程序化广告场景中DSP在对接ADX时进行广告投放的流程，如图1所示。该程序化广告投放流程即实时竞价（Real Time Bidding，RTB）。当用户访问网站时，网站向ADX发起广告请求，然后ADX向各DSP发起出价请求，DSP根据当前请求召回匹配的广告，预估广告点击率、转化率，同时还会预估当前请求的竞胜出价分布以指导出价，在上述预估的基础上，DSP使用某种出价策略计算出价，向ADX返回广告和相应出价，ADX对各DSP返回的广告和相应出价进行竞价，选择出价最高的广告胜出，并向网站返回广告进行展示，同时，将第二高的出价作为竞胜价格向胜出的DSP发送计价请求，即计价方式为展现计价，竞价机制为广义二价拍卖（GSP），广告展示后发生的用户行为（如点击、转化等）也会发送给DSP，用于统计分析和模型训练。

关于广告点击率、转化率预估的详细介绍可以进一步阅读笔者梳理的下述阅读笔记：

关于使用某种出价策略计算出价以实现自动出价的详细介绍可以进一步阅读笔者梳理的下述阅读笔记：

本篇主要是对较早一篇关于竞胜出价分布预估的论文——《Bid Landscape Forecasting in Online Ad Exchange Marketplace》的阅读笔记，介绍其方案。如有不足之处，请指正。

整体方案

论文首先介绍其目标是预估某个广告计划的竞胜出价分布，而广告计划一般会进行定向设置，这些定向设置由多个定向属性组成，每个定向属性可指定特定的一个或多个值，或不指定，且定向设置可能会随时间不断变化，例如，某一个广告计划定向地理位置在某些特定地域且广告请求来自某些特定媒体的用户，另一个广告计划先定向对电影感兴趣的用户，后定向对体育感兴趣的用户。通过进行定向设置，广告可以投放至特定的用户或媒体，从而满足广告计划的个性化投放诉求，提升广告计划的投放效果。

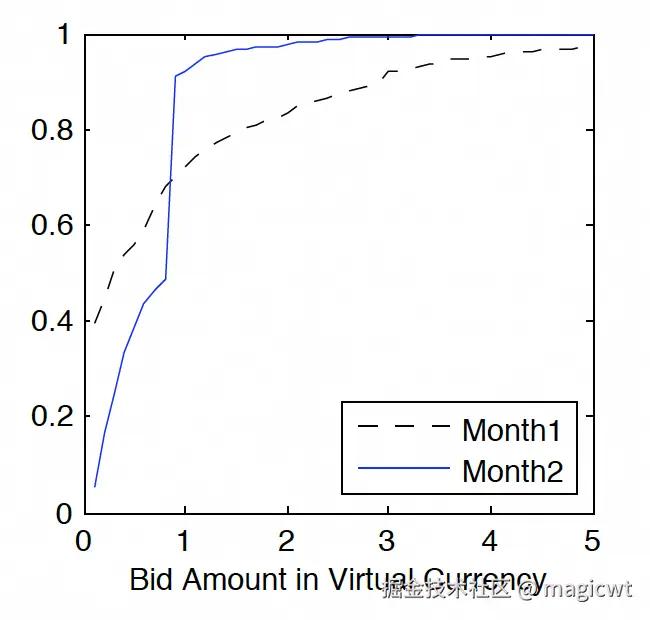
但广告计划中定向设置的个性化和多变性也给广告计划的竞胜出价分布预估带来挑战。广告计划中定向设置的变化，导致满足该定向设置的广告流量和预算供给的变化，进而导致该广告计划面对的广告竞价环境的变化，最终导致该广告计划竞胜出价分布的变化。例如，图2是某个广告计划在两个月份中的出价和累计竞得流量占比曲线，其中，虚线是月份一，实线是月份二，横坐标是出价，纵坐标是累计竞得流量占比，随着出价增大，累计竞得流量占比增大，直至最终为1，即竞得所有流量，从中可以看出，月份一和月份二的曲线并不一致，差异较大，验证了同一个广告计划在不同时间段下竞胜出价分布的多变性。

图2 某个广告计划在两个月份中的出价和累计竞得流量占比曲线

针对上述挑战，论文将对某个广告计划进行竞胜出价分布预估，转化为先对广告计划定向设置中的各个定向属性组合分别进行竞胜出价分布预估，最后再对各个定向属性组合的竞胜出价分布预估进行聚合，从而得到广告计划的竞胜出价分布预估。

例如，某个广告计划定向设置是：媒体（publisher）指定P1和P2这两个媒体，性别指定男，年龄指定18至23和30至35这两个年龄段。上述定向设置可以拆解为四个定向属性组合：

s1: publisher=P1, gender=male, age in (18-23)

s2: publisher=P2, gender=male, age in (18-23)

s3: publisher=P1, gender=male, age in (30-35)

s4: publisher=P2, gender=male, age in (30-35)

然后使用模型分别预估上述四个定向属性组合的竞胜出价分布。因为模型在定向属性组合粒度进行训练和预估，所以模型训练和预估的一条样本对应一个定向属性组合，因此，论文中的样本（sample）即定向属性组合，后续文中样本和定向属性组合可能会交替使用，但两者等价。

论文的整体方案如图3所示，其包含图3左侧的离线流程和图3右侧的在线流程。

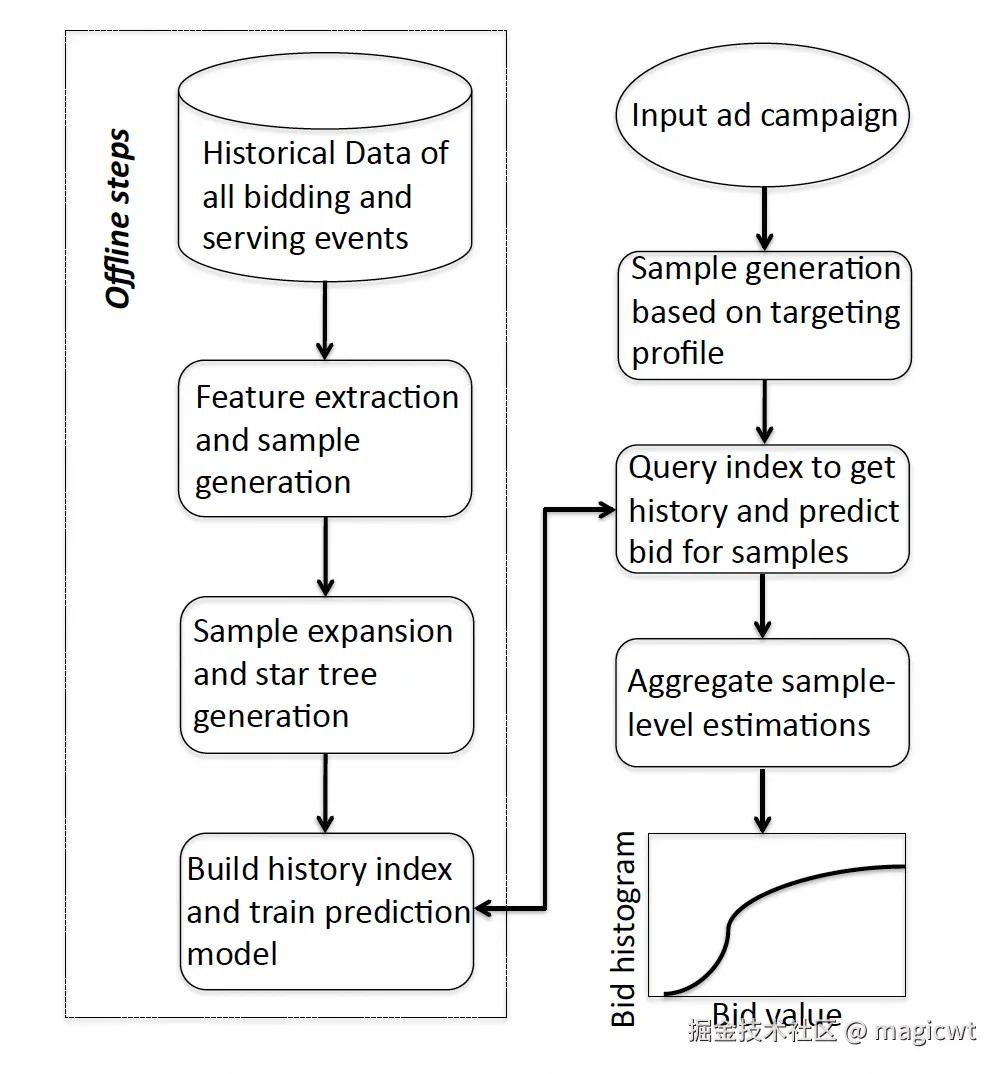
图3 整体方案

在线流程包含三步：

Sample generation based on targeting profile，将广告计划定向设置拆分为多个样本；
Query index to get history and predict bid for samples，论文认为样本的历史竞胜出价信息是一个比较重要的特征，因此从索引中查询样本的历史竞胜出价信息，并结合其它特征，预估样本的竞胜出价分布；
Aggregate sample-level estimations，聚合各样本的竞胜出价分布，得到广告计划的竞胜出价分布；

离线流程包含四步：

Data preprocessing，收集历史出价日志，对数据进行预处理，得到定向属性组合粒度的样本数据；
Feature extraction，采用一定的特征选择算法筛选和定向相关的特征，对特征进行精简；
History index building，采用一定的结构和算法构建索引，用于根据定向属性组合查询相应的历史竞胜出价信息；
Prediction model training，采用一定的算法和模型进行训练，用于根据定向属性组合预估相应的竞胜出价分布；

稍展开其中的一些细节。

特征选择算法论文使用了快速相关性过滤算法（Fast-Correlation Based Filtering，FCBF），通过该算法删除和定向无关的特征，或和其他特征冗余的特征（而其他特征和定向的相关性更高），该算法使用对称不确定性（Symmetric Uncertainty，SU）计算特征和定向的相关性：

SU(X,Y)=2\frac{IG(X|Y)}{H(X)+H(Y)}

其中， $IG$ 表示信息增益（Information Gain）， $IG(X|Y)$ 表示给定 $Y$ 时 $X$ 的信息增益，且 $IG(X|Y)=IG(Y|X)$ ， $H(X)$ 、 $H(Y)$ 分别表示 $X$ 、 $Y$ 的基数，即通过基数对信息增益进行归一化得到对称不确定性，若 $SU(X,Y)=1$ ，则 $X$ 和 $Y$ 完全相关，可以由 $X$ 推导出 $Y$ ，也可以由 $Y$ 推导出 $X$ ，而若 $SU(X,Y)=1$ ，则 $X$ 和 $Y$ 完全独立。

论文分析样本（即定向属性组合）的历史竞胜出价，历史竞胜出价呈现长尾效应，大量曝光的竞胜出价很低，且出价较分散，但有一批曝光的竞胜出价较高，且出价较集中，因此出价的对数和出价所对应的曝光数所构成的柱状图呈现正态分布，即样本的竞胜出价分布满足对数正态分布，某个样本的出价的对数和出价所对应的曝光数所构成的柱状图如图4所示。

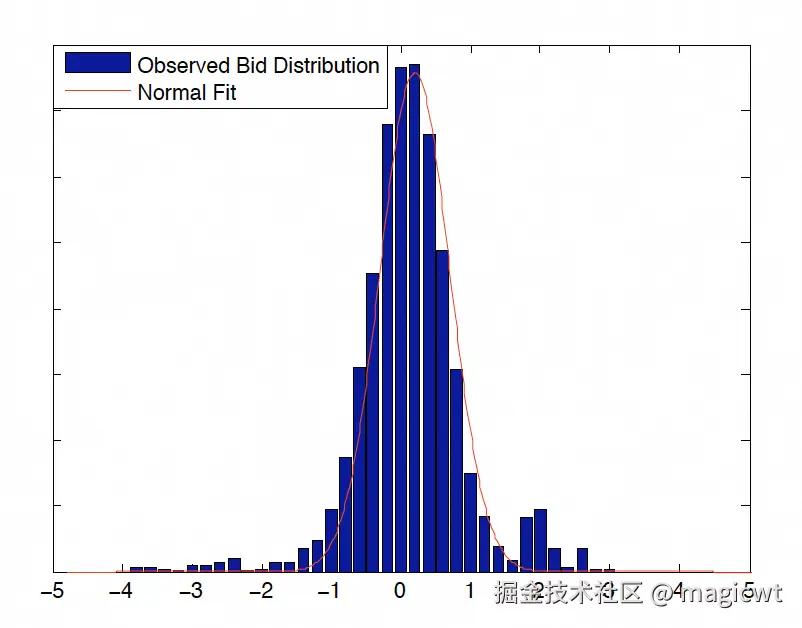
图4 某个样本的出价的对数和出价所对应的曝光数所构成的柱状图

基于上述分析，样本的竞胜出价分布满足对数正态分布，因此样本的历史出价信息只需要记录正态分布的均值和标准差，而预估样本的竞胜出价分布时，也只需要预估正态分布的均值和标准差。

论文进一步使用了一种树索引实现样本的历史出价信息的存储和查询，并使用了集成学习中的梯度提升决策树实现样本的竞胜出价分布的预估，下面会详细介绍出价历史查询、出价分布预估、出价分布聚合的细节。

出价历史查询

整体方案中已提到样本的历史竞胜出价信息是一个比较重要的特征，因此在线预估流程中需要从索引中查询样本的历史竞胜出价信息，并结合其它特征，预估样本的竞胜出价分布。

而样本的竞胜出价分布满足对数正态分布，因此样本的历史出价信息只需要记录正态分布的均值和标准差，而预估样本的竞胜出价分布时，也只需要预估正态分布的均值和标准差。

样本的历史出价信息的索引构建和查询方法分为两步：

第一步，树索引构建，并扩展已有样本，覆盖尽可能多的样本（即定向属性组合）；

第二步，根据模板查询，对于需预估的样本，从树索引中根据模板查询其历史竞胜出价的均值和标准差。

树索引构建

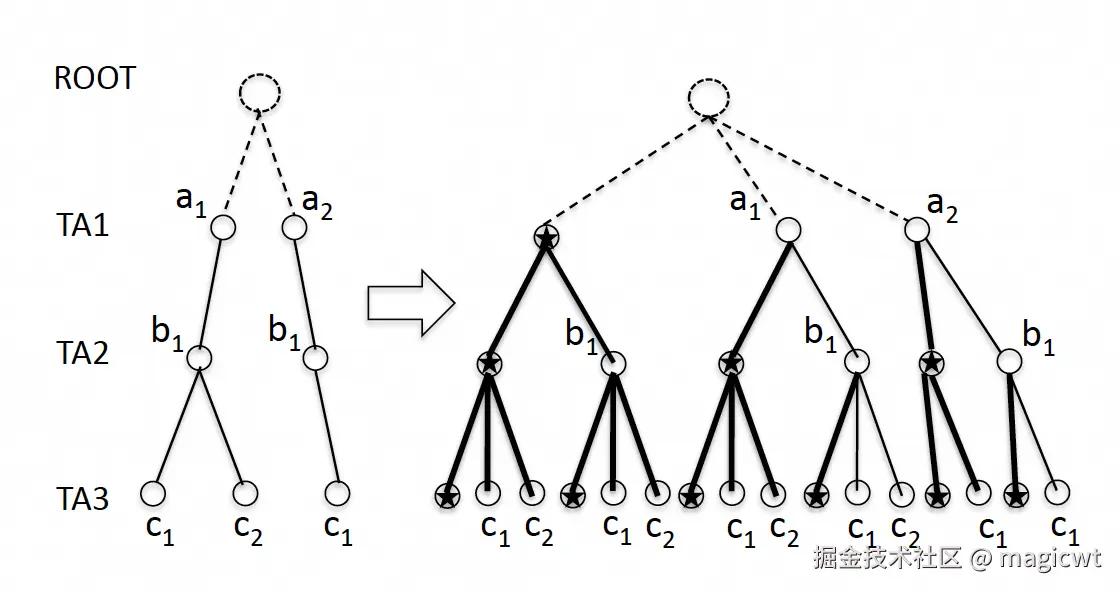
图5 基础树索引和扩展样本后、带有星形节点的树索引的示例

基础树索引的示例如图5左侧所示，其基于历史样本构建，其中树的每层表示一个定向属性，从根节点开始逐层往下，第1层的定向属性为TA1，其可能的取值有2个：a1和a2，第2层的定向属性为TA2，其可能的取值有1个：b1，第3层的定向属性为TA3，其可能的取值有2个：c1和c2。

从根节点至某个叶子节点构成一条路径，其表示一个历史样本，也就是一个历史定向属性组合，后续文中路径、样本和定向属性组合可能会交替使用，但三者等价。图5左侧所示的基础树索引共有三条路径，分别是：

a1, b1, c1

a1, b1, c2

a2, b1, c1

路径的叶子节点中存储了该路径所对应的样本的历史竞胜出价的均值和标准差。

基础树索引存在以下不足：

树中路径表示历史中存在曝光的定向属性组合，如果某个定向属性组合之前没有曝光，则不会出现在树中，例如“a2, b1, c2”；
即使某个定向属性组合出现在树中，但若其曝光比较稀疏，则该定向属性组合的历史竞胜出价的均值和标准差不置信；
基础树索引无法处理的一个场景是，若某个定向属性不指定某个特定值，即该定向属性可取取值范围内的任意一个值，例如，年龄可取任意年龄段，而不指定某个特定年龄段，地域可取全国，而不指定某个特定地域，则无法从基础树索引中查询到相应的路径；

为了解决上述问题，论文为每个定向属性引入一个特殊取值，即星形符号“ $*$ ”，该特殊取值表示定向属性不指定某个特定值，即“targeting all”。图5左侧基础树索引在引入定向属性的特殊取值后，带有星形符号的新树索引如图5右侧所示，论文称之为“Star Tree”。新树索引在原有三个路径的基础上，增加了以下13条路径：

*, *, *

*, *, c1

*, *, c2

*, b1, *

*, b1, c1

*, b1. c2

a1, *, *

a1, *, c1

a1, *, c2

a1, b1, *

a2, *, *

a2, *, c1

a2, b1, *

a1, b1, c1

每个路径的叶子节点存储了满足该路径所对应定向属性组合的历史曝光的竞胜出价的均值的标准差。某个历史曝光可能匹配至多条路径，例如，某个历史曝光的定向属性组合为“a1, b1, c1”，则其可以匹配的路径包括：

*, *, *

*, *, c1

*, b1, *

*, b1, c1

a1, *, *

a1, *, c1

a1, b1, *

因此，这个历史曝光的竞胜出价会参与上述7个路径的叶子节点存储的历史竞胜出价的均值和标准差的计算。

而对某个样本预估竞胜出价分布，需从新树索引中查询该样本所对应的路径时，若在新树索引中并没有精确匹配的路径，则可以通过星形符号节点进行近似匹配，例如，若需查询样本“a2, b1, c2"所对应的路径，新树索引中并没有精确匹配的路径，而近似匹配的路径则有：

a2, b1, *

*, b1, c2

而预估的样本具体使用上述近似匹配路径中的哪个路径的历史竞胜出价的均值和标准差呢？下面一节会介绍根据模板查询的方法。

另外，针对某个定向属性组合的曝光较稀疏，其历史竞胜出价的均值和标准差不置信的问题，论文对新树索引中曝光稀疏的路径进行剪枝，从而保证剪枝后剩下路径的置信度。虽然被剪枝的路径在新树索引中不再存在，后续与该路径对应的样本预估时无法精确匹配到该路径，但可近似匹配到其他置信的路径。

最后，引入星形符号节点，也便于预估的样本若对某个定向属性不作取值限制，即“targeting all”时，可从新树索引中查询到精确或近似匹配的路径。从而解决了基础树索引存在的若干问题。

根据模板查询

对于预估的样本，如何从新树索引中查询对应的路径？简单来说，首先从树索引中查询精确匹配的路径，若能找到，则直接使用精确匹配的路径，若未找到，则从树索引中查询近似匹配的路径，若近似匹配的路径存在多条，则使用与原样本有最多相同节点的路径。

首先引入模板定义。对于每个定向属性，有两个匹配类型，一个是精确匹配，用“ $v$ ”表示，一个是近似匹配，用“ $*$ ”表示。模板是各个定向属性匹配类型的组合。令有 $D$ 个定向属性，则某个模板可表示为：

T_k=[T_{k1}T_{k2}...T_{kd}...T_{kD}]

其中， $T_{kd}\in\{*,v\}$ 。

令 $s_i$ 表示某个样本。定义样本 $s_i$ 和模板 $T_k$ 的掩码计算：

s_i'=s_i\oplus T_k

其中，若 $T_{kd}=v$ ，则 $s_{id}'=s_{id}$ ，即 $s_i'$ 中第 $i$ 个定向属性取值保持和 $s_i$ 一致，不变，若 $T_{kd}=*$ ，则 $s_{id}'=*$ ，即 $s_i'$ 中第 $i$ 个定向属性取值被改为 $*$ 。然后从树索引中查询路径 $s_i'$ ，如果 $s_i'$ 在树索引中存在，则找到一个与样本 $s_i$ 匹配的路径。举例说明，若 $s_i=a_2b_1c_2$ ， $T_k=[vv*]$ ，则 $s_i'=a_2b_1*$ 。

论文还定义了 $s_i$ 和 $s_i'$ 的相似分：

simScore(s_i,s_i')=\sum_{d=1}^D{\lambda_d\delta(s_{id},s_{id}')}

其中， $\lambda_d$ 表示第 $d$ 个定向属性 $TA_d$ 的权重分。论文同样使用对称不确定性（Symmetric Uncertainty，SU）计算定向属性 $TA_d$ 和出价的相关性作为 $TA_d$ 的权重分。

\lambda_d=SU(TA_d,bid)

$\lambda_d$ 取值非负，且在0和1之间，取值为1表示定向属性和出价完全相关，权重最高，取值为0表示定向属性和出价完全独立，权重最低。而 $\delta(s_{id},s_{id}')$ 的取值如下

\delta(s_{id},s_{id}') = \begin{cases} 1 &\text{if } s_{id}=s_{id}' \\ c &\text{otherwise } \end{cases}

另外，论文定义了模板质量分：

qualityScore(T_k)=\sum_{d=1}^D{\lambda_d\delta(T_{kd},v)}

即模板中， $v$ 越多，通过模板对样本进行掩码计算后得到的新路径与原样本越接近，因此模板的质量分越高，若模板中全是 $v$ ，没有 $*$ ，则通过模板对样本进行掩码计算后得到的新路径与原样本一致，因此模板的质量分最高。

模板数量随定向属性数量的增长指数级增长，若有20个定向属性，则有 $2^{20}$ 个模板。极限情况下，我们需要对上述模板按质量分从高到低排序，质量分最高的模板全是 $v$ ，质量分最低的模板全是 $*$ ，然后遍历每个模板，通过模板对样本进行掩码计算后得到新路径，然后从树索引中查询与该新路径一致的路径，因此计算量比较大。

如何减少模板数量从而减少计算量？论文提出如图6所示的算法1，从全部模板中挑选 $K$ 个模板用于掩码计算和路径匹配。

图6 挑选模板的算法的伪代码

令有 $N$ 个训练样本 $\{s_1,s_2,...,s_N\}$ ，每个样本有相应的曝光数 $\{imp_1,imp_2,...,imp_N\}$ ，每个样本有 $D$ 个定向属性，每个定向属性有相应的权重分 $\lambda=(\lambda_1,...,\lambda_D)$ 。算法1的主要逻辑：

第2至4行，计算各模板的质量分；
第5行，对模板按其质量分降序排序，质量分最高排第一的是全是 $v$ 的模板，质量分最低排最后的是全是 $*$ 的模板；
第6至第11行，计算各模版对样本的覆盖分，这里遍历每个样本，对于每个样本，遍历模板排序列表中的每个模板，对模板和样本进行掩码计算得到路径，直至在树中能够找到该路径，则将当前样本的曝光数累加至当前模板的覆盖分；
第12行，对模板按其覆盖分降序排序，选取前 $K$ 个模板；
第13行，因为全是 $*$ 的模板在和样本进行掩码计算后得到全是 $*$ 的路径，而全是 $*$ 的路径在树索引中必然存在，所以论文将全是 $*$ 的模板作为兜底模板，若全是 $*$ 的模板不在已选取的 $K$ 个模板中，则将 $K$ 个模板中的最后一个模板替换为全是 $*$ 的模板；
第14行，返回最终选取的 $K$ 个模板。

算法1离线计算。在线计算时，对于预估样本，将其并行与离线挑选出的 $K$ 个模板进行掩码计算得到相应的路径，在树索引中查找路径，然后选择能找到的、且模板质量分最高的路径中存储的历史竞胜出价的均值和标准差。

出价分布预估

论文使用集成学习中的梯度提升决策树（Gradient Boosting Decision Tree，GBDT）实现样本的竞胜出价分布的预估，模型输入除上一节查出的历史竞胜出价的均值和标准差外，还包括用户和媒体特征，模型输出是竞胜出价分布的均值和标准差。

对出价分布预估问题进行建模。给定训练样本集 $\{(\mathbf{x}_i,y_i)\}_{i=1}^N$ ，其中， $\mathbf{x}_i\in\mathcal{X}$ ，表示样本， $y_i\in\mathcal{Y}$ ，表示样本竞胜出价分布的均值和标准差的真实值，目标是求解最优函数 $F^*(\mathbf{x})$ ，其返回样本竞胜出价分布的均值和标准差的预估值，且使得预估值和真实值之间的最小平方损失函数值最小，即：

F^*(\mathbf{x})=\arg\min_{F(\mathbf{x})}E_{y,\mathbf{x}}\{\mathcal{l}(y,F(\mathbf{x}))\}

其中， $l(y,F(\mathbf{x}))$ 表示最小平方损失函数。

集成学习方法大致可分为两大类，如图7所示，即个体学习器间存在强依赖关系、必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系、可同时生成的并行化方法；前者的代表是Boosting，后者的代表是Bagging和“随机森林”（Random Forest）。

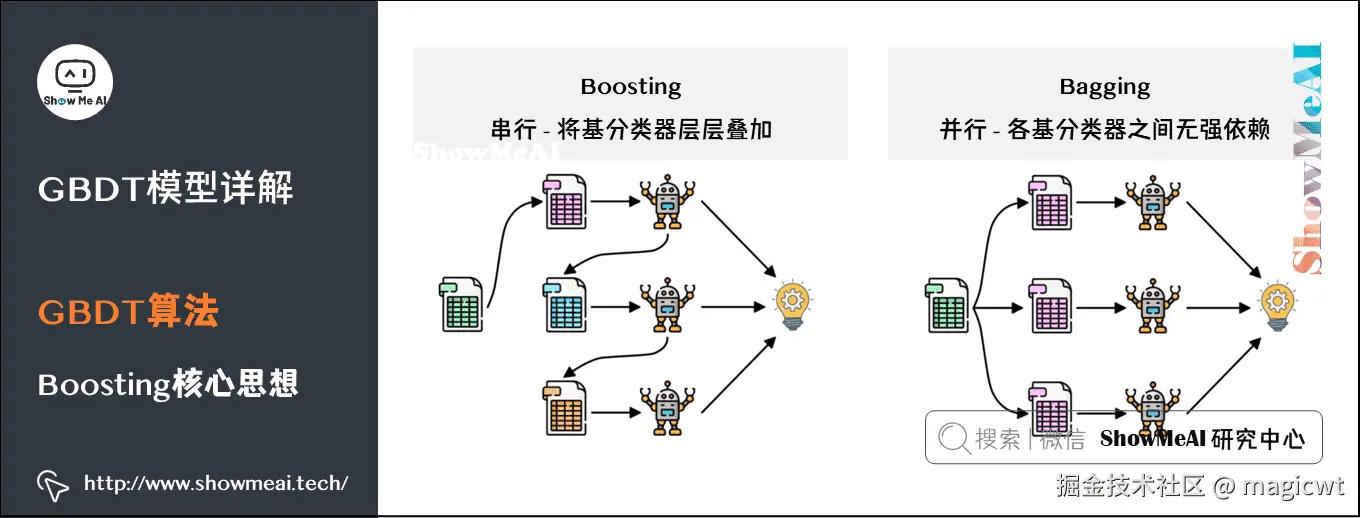
图7 集成学习两大类

Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本进行调整，使得先前基学习器做错的训练样本在后续受到更多关注。然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值，最终将上述各基学习器进行加权结合。

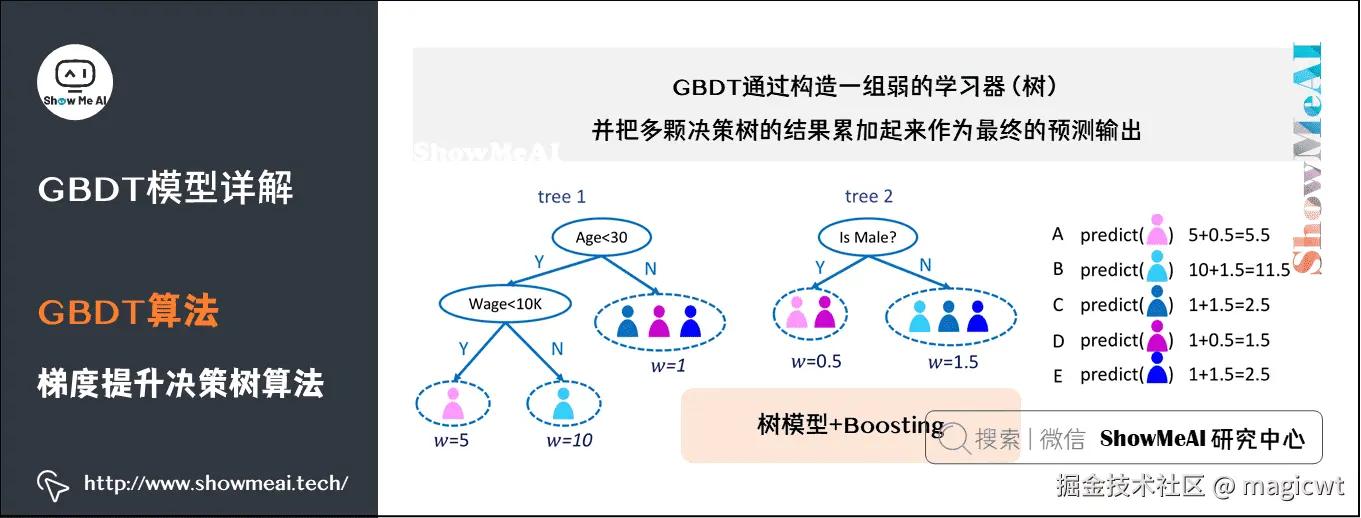
梯度提升决策树（Gradient Boosting Decision Tree，GBDT）属于Boosting方式的集成学习，使用决策树作为基学习器，通过梯度提升决策树进行训练和推理的示例如图8所示，其中使用两棵决策树进行训练和推理，对于图8中粉红色标注的用户，其真实值是5.5，训练时，若第一棵树的预估值是5，则第二棵树需预估的真实值为第一棵树真实值和预估值的差值——0.5，而推理时，若第一棵树的预估值是5，第二棵树的预估值是0.5，则最终整体的预估值是5.5。

图8 通过GBDT进行推理的示例

论文使用标准的梯度提升决策树算法，训练时对 $F(\mathbf{x})$ 进行多轮迭代，每轮迭代构建一棵新树，初始时， $F(\mathbf{x})$ 即取所有样本真实值的平均值，如下所示：

F_0(\mathbf{x})=\frac{1}{N}\sum_{i=1}^N{y_i}

第 $m$ 轮迭代时，构造一棵新树 $h(\mathbf{x};\mathbf{a})$ ，通过训练求取新树的参数 $\mathbf{a}_\mathbf{m}$ ，使得新树对于训练样本集中各样本的预估值，能够尽量拟合真实值和已有 $F(\mathbf{x})$ 预估值的差值，即：

\mathbf{a}_{\mathbf{m}}=\arg\min_{\mathbf{a}}\sum_{i=1}^N{[y_i-F_{m-1}(\mathbf{x}_\mathbf{i})-h(\mathbf{x}_\mathbf{i};\mathbf{a})]^2}

该轮迭代完成后，将新树 $h(\mathbf{x};\mathbf{a})$ 的预估值，累加至已有 $F(\mathbf{x})$ 预估值上，即：

F_m(\mathbf{x})=F_{m-1}(\mathbf{x})+h(\mathbf{x};\mathbf{a}_\mathbf{m})

出价分布聚合

在得到各样本的竞胜出价分布后，聚合各样本的竞胜出价分布，得到广告计划的竞胜出价分布。

每个样本 $s$ 的竞胜出价的对数满足正态分布：

x=bid(s)\sim Log - \mathcal{N}(\mu,\sigma^2)

样本 $s$ 的竞胜出价的概率密度函数计算公式为：

f_s(x;\mu,\sigma)=\frac{1}{x\sigma\sqrt{2\pi}}e^{\frac{-(lnx-\mu)^2}{2\sigma^2}},x\gt 0

基于上一节预估得到的样本 $s$ 的竞胜出价的均值和标准差，可由下式得到上述概率密度函数的 $\mu$ 和 $\sigma^2$ ：

\mu=ln(E[s])-\frac{1}{2}ln(1+\frac{std[s]^2}{E[s]^2})

\sigma^2=ln(1+\frac{std[s]^2}{E[s]^2})

广告计划的竞胜出价的概率密度函数计算公式可表示为：

f(X|x;\theta_1,\theta_2,...,\theta_C;\pi_1,\pi_2,...,\pi_C)=\sum_{j=1}^C{\pi_j\frac{1}{x\sigma_j\sqrt{2\pi}}e^{\frac{-(lnx-\mu_j)^2}{2\sigma^2_j}}}

其中， $0\lt \pi_j\lt 1$ ， $\sum_{j=1}^C{\pi_j}=1$ ，即组成该计划定向设置的各样本的竞胜出价的概率密度函数的加权和。

图9 在线计算广告计划的竞胜出价分布的伪代码

算法2定义函数getBidHistogram，用于在线计算广告计划的竞胜出价分布，其输入包括广告计划、已选取的 $K$ 个模板、包括历史出价信息的树索引、梯度提升决策树模型，输出为广告计划的竞胜出价分布。

函数getBidHistogram的主要流程：

第2行，将广告计划的定向设置拆分为 $N$ 个样本。
第3行至第8行，对于每个样本 $s_i$ ，分别和 $K$ 个模板进行掩码计算，得到 $K$ 个路径，然后并发从树索引中查找这 $K$ 个路径，对于能从树索引中查找到的路径，选择模板质量分最高的路径 $s_i'$ ，并从树索引中查找该路径所对应的历史竞胜出价的均值 $\tilde{E}(s_i')$ 和标准差 $\tilde{std}(s_i')$ ，然后通过梯度提升决策树模型预估样本 $s_i$ 竞胜出价分布的均值 $\hat{E}(s_i)$ 和标准差 $\hat{std}(s_i)$ ，最后再通过本节的公式得到竞胜出价对数分布的均值 $\hat{\mu_i}$ 和方差 $\hat{\sigma^2_i}$ ；
第9行，聚合各样本的竞胜出价分布，得到广告计划的竞胜出价分布。

Bid Landscape论文阅读笔记

概述