人工智能|软间隔：让支持向量机更“宽容”

在SVM中，软间隔是一个重要的概念，它允许模型在一定程度上容忍误分类，从而提高模型的泛化能力。

本文将详细介绍软间隔的定义、与硬间隔的区别、损失函数的作用，最后使用 scikit-learn 进行实际演示。

1. 软间隔 vs 硬间隔

在支持向量机中，软间隔是指允许某些数据点违反分类边界（即误分类）的间隔。

与硬间隔（严格要求所有数据点都正确分类）不同，软间隔通过引入松弛变量（slack variables），允许部分数据点位于分类边界内或错误分类，从而优化分类边界。

与硬间隔相比，软间隔的优势非常明显，因为在现实世界中，数据往往存在噪声和异常值，很难找到一个完美的分类边界将所有数据点正确分类。

硬间隔 SVM 在这种情况下可能会导致过拟合，即模型在训练数据上表现很好，但在新的测试数据上表现不佳。

软间隔通过允许一定的误分类，能够更好地处理噪声和异常值，从而提高模型的泛化能力。

不过，软间隔也有自己的劣势，它需要选择合适的松弛变量参数（如惩罚参数 $C$ ），否则可能导致欠拟合或过拟合。

参数选择的不好，效果可能还不如硬间隔。

2. 软间隔中的损失函数

在软间隔SVM中，需要通过损失函数来实现容错机制，并通过优化损失函数来训练模型。

常见的损失函数主要有4种：

2.1. Hinge Loss

它的公式是： $L(y,f(x))=max(0,1-y\cdot f(x))$

其中， $y$ 是真实标签（+1或-1）， $f(x)$ 是模型的预测值。

Hinge Loss 是 SVM 的经典损失函数，它惩罚那些被错误分类或接近分类边界的点。

如果数据点被正确分类且距离分类边界较远，则损失为零；否则，损失值会随着距离的减小而增加。

Hinge Loss 适合线性可分的数据，但在处理噪声和异常值时可能不够灵活。

2.2. Squared Hinge Loss

它的公式是： $L(y,f(x))=max(0,1-y\cdot f(x))^2$

与 Hinge Loss 类似，但对误分类的惩罚更严厉，因为损失值是平方的。

Squared Hinge Loss 对噪声和异常值的惩罚更重，可能导致模型对这些点更敏感。

在某些情况下，这可以提高模型的鲁棒性，但也可能增加过拟合的风险。

2.3. Logistic Loss

它的公式是： $L(y,f(x))=log(1+exp(-y\cdot f(x)))$

Logistic Loss 是逻辑回归中常用的损失函数，它对所有数据点都有惩罚，但惩罚程度随着距离分类边界的增加而逐渐减小。

Logistic Loss 适合处理非线性可分的数据，因为它对所有数据点都有惩罚，但对误分类的惩罚相对较轻。这使得模型在处理噪声和异常值时更加灵活。

2.4. Smooth Hinge Loss

它的公式是： $L(y, f(x)) = \begin{cases} 0 & \text{if } y \cdot f(x) \geq 1 \\ 1 - y \cdot f(x) & \text{if } 0 < y \cdot f(x) < 1 \\ \frac{(1 - y \cdot f(x))^2}{2} & \text{if } y \cdot f(x) \leq 0 \end{cases}$

Smooth Hinge Loss 是 Hinge Loss 的平滑版本，它对误分类的惩罚更加平滑，避免了 Hinge Loss 的不连续性。

Smooth Hinge Loss 在优化过程中更加稳定，适合使用梯度下降等优化算法，它对噪声和异常值的处理也更加灵活。

3. 软间隔实践

为了直观地展示软间隔和硬间隔的区别，我们使用scikit-learn构造一个简单的线性可分数据集，并分别训练硬间隔和软间隔SVM。

3.1. 软间隔和硬间隔比较

为了比较软间隔和硬间隔的效果，我们构造一个比较难于线性划分的数据。


python
 代码解读
复制代码
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 生成线性可分的数据集
X, y = make_blobs(n_samples=100, centers=2, random_state=42, cluster_std=4)

# 绘制数据集
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
plt.title("非线性可分数据集")
plt.show()

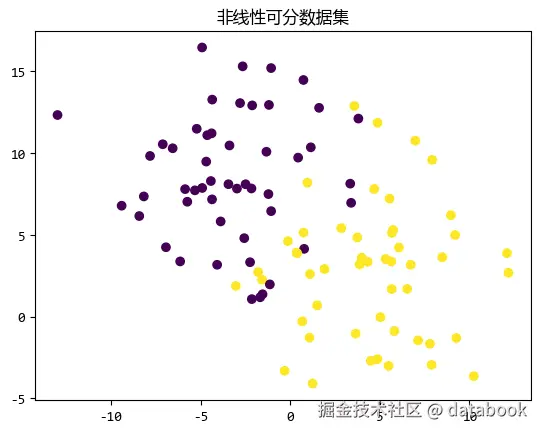
两类数据有交织的部分，无法用一条直线来划分。

然后分别用硬间隔和软间隔的支持向量机来训练。


python
 代码解读
复制代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
import time

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# 硬间隔 SVM
svm_hard = SVC(kernel="linear", C=1e10)  # 大的 C 值近似硬间隔
svm_hard.fit(X, y)
y_pred_hard = svm_hard.predict(X_test)
print("硬间隔的准确率：", accuracy_score(y_test, y_pred_hard))

# 软间隔 SVM
svm_soft = SVC(kernel="linear", C=1.0)  # 较小的 C 值允许软间隔
svm_soft.fit(X, y)
y_pred_soft = svm_hard.predict(X_test)
print("软间隔的准确率：", accuracy_score(y_test, y_pred_soft))


# 绘制决策边界
def plot_decision_boundary(model, X, y, title):
    h = 0.02  # 网格间隔
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.contourf(xx, yy, Z, alpha=0.8, cmap="viridis")
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors="k", cmap="viridis")
    plt.title(title)
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")


# 绘制硬间隔和软间隔的决策边界
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plot_decision_boundary(svm_hard, X, y, "硬间隔 SVM")

plt.subplot(1, 2, 2)
plot_decision_boundary(svm_soft, X, y, "软间隔 SVM")

plt.tight_layout()
plt.show()

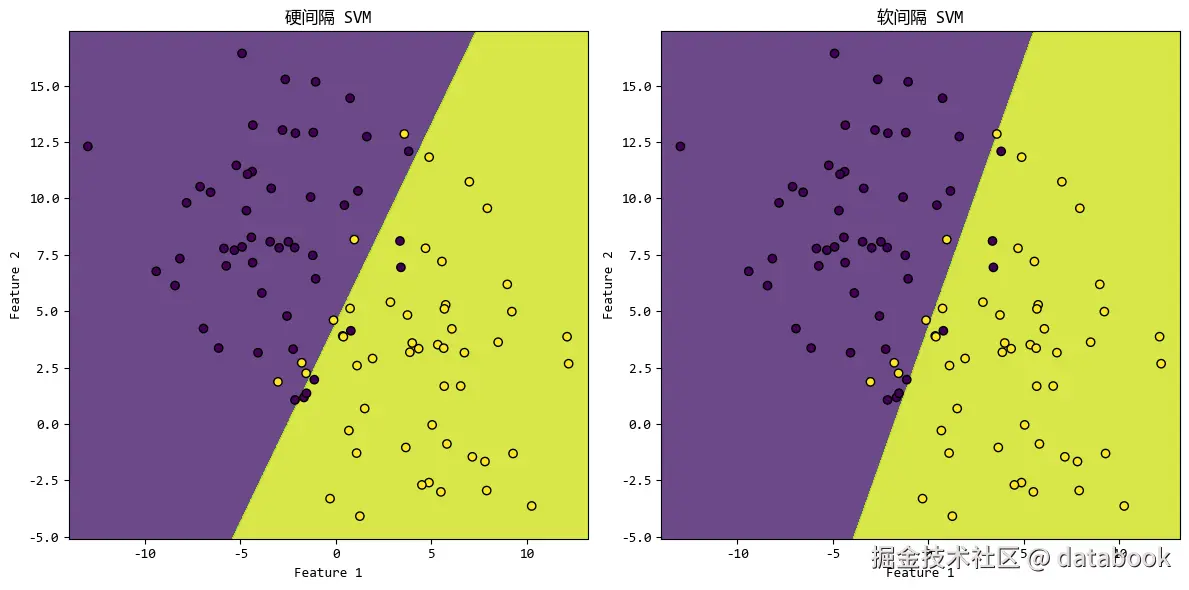
执行之后，软间隔和硬间隔的准确率都是 0.9，从图上来看似乎也只是略有区别。

其实软间隔相比硬间隔的优势不是准确率，可以说在很多情况下，硬间隔的准确率都是高于软间隔的。

那么这个示例中，软间隔的有时是什么呢？

如果你实际去运行上面的代码就会发现，上面两次训练（硬间隔模型和软间隔模型）的时间分别：

30.82秒和0.001秒，也就是软间隔模型的训练时间远远小于硬间隔模型的训练时间。

这还是在数据不复杂的情况，如果修改下数据，也就是上面创建数据的代码中，将：


python
 代码解读
复制代码
X, y = make_blobs(n_samples=100, centers=2, random_state=42, cluster_std=4)

其中的cluster_std的值调大一些的话，那么硬间隔模型的训练时间几乎无法忍受。

这才是软间隔模型的一大优势，准确率绝对不是软间隔模型的优势。

3.2. 不同损失函数比较

接下来演示不同损失函数对SVM训练效果的影响，我们使用 scikit-learn 构造一个简单的数据集，

然后用使用不同的损失函数来训练，并将训练结果用图形展示出来。


python
 代码解读
复制代码
from sklearn.linear_model import SGDClassifier

# 生成数据集
X, y = make_blobs(n_samples=100, centers=2, random_state=42, cluster_std=4)

# Hinge Loss (SVM)
svm_hinge = SGDClassifier(
    loss="hinge", alpha=0.01, max_iter=1000, tol=1e-3, random_state=42
)
svm_hinge.fit(X, y)

# Squared Hinge Loss (SVM)
svm_squared_hinge= SGDClassifier(
    loss="squared_hinge", alpha=0.01, max_iter=1000, tol=1e-3, random_state=42
)
svm_squared_hinge.fit(X, y)

# Logistic Loss (Logistic Regression)
svm_logistic = SGDClassifier(
    loss="log_loss", alpha=0.01, max_iter=1000, tol=1e-3, random_state=42
)
svm_logistic.fit(X, y)

# modified_huber
svm_mod_huber = SGDClassifier(
    loss="modified_huber", alpha=0.01, max_iter=1000, tol=1e-3, random_state=42
)
svm_mod_huber.fit(X, y)

# 绘制决策边界
plt.figure(figsize=(12, 12))

plt.subplot(2, 2, 1)
plot_decision_boundary(svm_hinge, X, y, "Hinge Loss")

plt.subplot(2, 2, 2)
plot_decision_boundary(svm_squared_hinge, X, y, "Squared Hinge Loss")

plt.subplot(2, 2, 3)
plot_decision_boundary(svm_logistic, X, y, "Logistic Loss")

plt.subplot(2, 2, 4)
plot_decision_boundary(svm_mod_huber, X, y, "Smooth Hinge Loss")

plt.tight_layout()
plt.show()

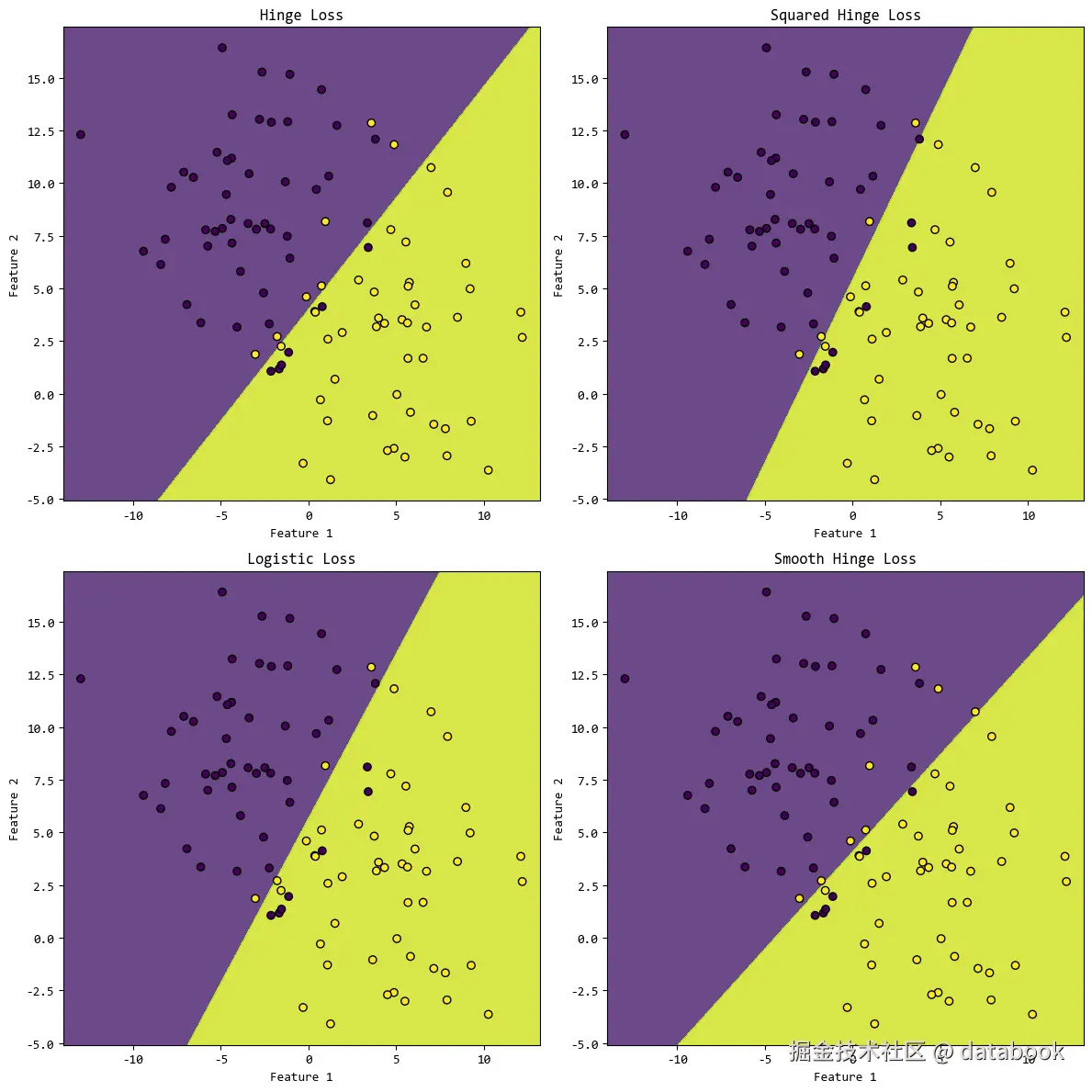
注意，scikit-learn中没有直接提供Smooth Hinge Loss这个损失函数的选项，modified_huber是与它最接近的损失函数。

损失函数的效果取决于数据的特征，没有最好的损失函数，只有最合适的损失函数。

实际场景中，需要根据数据的特点和需求选择合适的损失函数。

比如，数据线性可分且无噪声，可以选择 Hinge Loss；

如果数据存在噪声和异常值，可以选择 Logistic Loss 或 Smooth Hinge Loss。

4. 总结

软间隔通过松弛变量赋予SVM处理不完美数据的能力，配合不同损失函数可以灵活应对各种场景。

理解软间隔机制，掌握参数调优方法，是提升SVM实战性能的关键。

实际项目中，建议从Hinge Loss+RBF核开始实验，逐步探索参数空间，最终通过交叉验证确定最优配置。