前端|一杯蜜桃四季春的时间吃透一道高频面试算法题—

题目描述——旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：


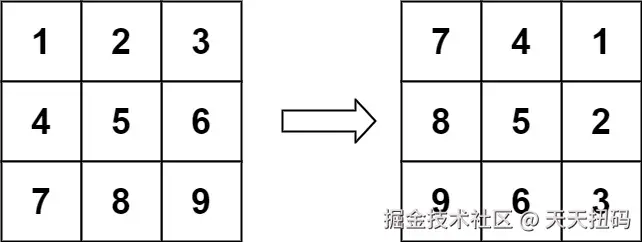
lua
 代码解读
复制代码
输入： matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出： [[7,4,1],[8,5,2],[9,6,3]]

示例 2：


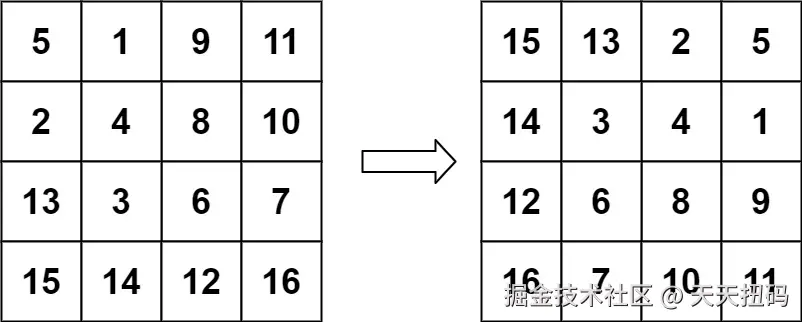
lua
 代码解读
复制代码
输入： matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出： [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

二、题解


js
 代码解读
复制代码
/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */

var rotate = function(matrix) {
    const n = matrix.length;
    
    // 逐层处理，外层到内层的边界
    for (let layer = 0; layer < Math.floor(n / 2); layer++) {
        const first = layer; // 当前层的起始索引
        const last = n - 1 - layer; // 当前层的结束索引
        
        // 遍历当前层的元素
        for (let i = first; i < last; i++) {
            const offset = i - first; // 当前元素的偏移量
            
            // 依次交换四个角的元素，实现旋转
            // 1. 保存 top-left
            const topLeft = matrix[first][i];
            
            // 2. 赋值 bottom-left 到 top-left
            matrix[first][i] = matrix[last - offset][first];
            
            // 3. 赋值 bottom-right 到 bottom-left
            matrix[last - offset][first] = matrix[last][last - offset];
            
            // 4. 赋值 top-right 到 bottom-right
            matrix[last][last - offset] = matrix[i][last];
            
            // 5. 将之前保存的 top-left 放入 top-right
            matrix[i][last] = topLeft;
        }
    }
};

核心思想：

将矩阵的旋转分解为逐层旋转。每一“层”可以想象成一个围绕矩阵的边框。对于一个 n x n 的矩阵，最多有 n / 2 层需要旋转（如果 n 是奇数，最中央的元素不需要旋转）。对于每一层，我们围绕其边界上的元素执行四路交换，模拟旋转 90 度的过程。即 Top -> Right, Right -> Bottom, Bottom -> Left, Left -> Top。

详细解释：

分层旋转 (Layer-by-Layer Rotation):
- 算法的核心思想是，将整个正方形矩阵的旋转，转化为对矩阵每一圈元素的旋转。想象一下，一个嵌套的正方形，从最外层开始，逐步向内。
- 对每一层独立地执行旋转操作。
- Math.floor(n / 2) 确定了需要处理的“层”的数量。如果 n 是奇数，那最中心的单个元素或者小的 1x1 方块是不需要旋转的。
边界确定 (Boundary Definition):
- first = layer：当前层的起始索引，代表从矩阵最外侧的第 layer 层开始处理。
- last = n - 1 - layer：当前层的结束索引，代表到矩阵内侧的第 layer 层结束。
四路交换 (Four-Way Swap):
- 这是实现旋转的关键。对于当前层的每一个元素（除了最后一个），执行四次赋值操作，模拟元素旋转到新的位置：
  - topLeft = matrix[first][i] : 保存当前层的“左上角”的值。这个值会被后续的赋值覆盖，因此需要保存起来。这里的“左上角”实际上指的是当前行从左至右的某个元素。
  - matrix[first][i] = matrix[last - offset][first] : 将底部的元素移动到顶部。该行的index为first, 列的index为 i, last - offset是底部对应位置的索引，从而实现底部->顶部。
  - matrix[last - offset][first] = matrix[last][last - offset] : 将右侧的元素移动到底部。 last是底部的行index. last - offset 是右侧列的index.
  - matrix[last][last - offset] = matrix[i][last] : 将顶部的元素移动到右侧。 i 为顶部的行。last为右侧的列，
  - matrix[i][last] = topLeft: 将临时保存的左上角元素（初始值）移动到左侧。topLeft保存开始旋转之前的顶部元素。现在旋转到左边了。
- 使用 offset 变量来确定每一边的对应元素，确保每一圈都能正确旋转。

注意事项：

理解层的概念： 代码中 “层” 是指从矩阵外向内的一圈圈的元素。要理解外圈如何影响内圈。
坐标计算： 需要非常小心计算行和列的索引，尤其是在使用 offset 的时候。确保正确对应需要交换的四个元素。
边界条件： for (let i = first; i < last; i++) 中的 i < last 是为了避免重复操作最后一个元素。例如一个4x4 的矩阵，在layer=0时， i的取值为 0,1,2。
原地操作： 理解为什么这个算法可以原地旋转矩阵。它只使用了有限的几个变量（layer, first, last, i, offset, topLeft）来辅助旋转，不需要额外的矩阵空间。
调试： 调试的时候可以使用小规模的矩阵，手动模拟坐标的改变，能更好地理清代码的逻辑。
避免混淆： i 用来遍历一行的元素，layer用来表示不同的圈层, offset用来根据当前圈层计算对应位置，first确定每一圈的起始坐标 last 确定结束坐标。

三、结语

再见！

一杯蜜桃四季春的时间吃透一道高频面试算法题——旋转图像