一、问题回顾:接雨水问题的两种解法对比
题目要求:给定一个非负整数数组表示柱子的高度,计算这些柱子排列后能接多少雨水。
示例分析:
以输入 [0,1,0,2,1,0,1,3,2,1,2,1] 为例,其结构如下:
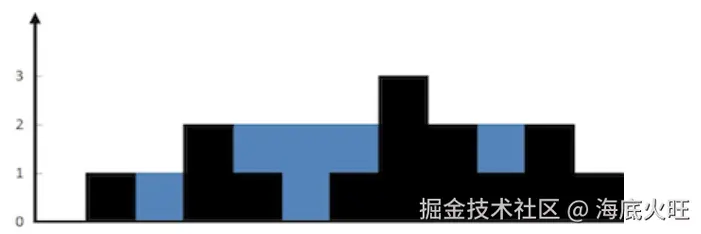
可存储 6个单位的雨水。
二、分层法的局限:为何超时?
这里一开始我是想要算出每一层的面积,加起来,然后减去height的总和,剩下的就是水量了。
原思路代码
javascript 代码解读复制代码function trap(height) {
const n = height.length;
if (n === 0) return 0;
let totalWater = 0;
let h = 1;
let left = 0;
let right = n - 1;
while (true) {
while (left < n && height[left] < h) {
left++;
}
while (right >= 0 && height[right] < h) {
right--;
}
// 检查
if (left > right) break;
// 计算当前层的有效宽度和统计符合条件的柱子数
const currentWidth = right - left - 1;
if (currentWidth <= 0) {
h++;
continue;
}
let count = 0;
for (let i = left + 1; i < right; i++) {
if (height[i] >= h) {
count++;
}
}
totalWater += currentWidth - count;
h++;
}
return totalWater;
}
console.log(trap([0,1,0,2,1,0,1,3,2,1,2,1])); // 6
console.log(trap([4,2,0,3,2,5])); // 9
问题分析:
- 时间复杂度高:对于最大高度为
H的数组,时间复杂度为O(H * n)。若H极大(如1e5),效率极低。 - 重复扫描:每一层都需要重新扫描数组,导致大量冗余计算。
示例缺陷:当输入为 [1e5, 0, 0, ..., 0, 1e5] 时,需要循环 1e5 层,性能无法接受。
所以在最后大量数据示例下运行超时。
三、双指针优化:O(n) 时间的智慧
这里就有夹逼的味道了,也有最短木板的想法。
优化后代码
javascript 代码解读复制代码var trap = function(height) {
let left = 0, right = height.length - 1;
let leftMax = 0, rightMax = 0;
let ans = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
left++;
} else {
ans += rightMax - height[right];
right--;
}
}
return ans;
};
核心思路
- 双指针夹逼:
left和right分别从数组两端向中间移动。 - 动态维护最大值:
leftMax记录左侧遍历过的最大高度。rightMax记录右侧遍历过的最大高度。
- 水位计算策略:
- 短板效应:当前水位由左右两侧较小的最大高度决定。
- 单侧积累:若
height[left] < height[right],则左指针处的水位由leftMax决定,反之同理。
正确性证明
- 局部最优性:每一步移动指针时,总是先处理高度较低的一侧,确保该侧的水位不会超过当前已知的较小最大值。
- 全局覆盖性:双指针遍历过程中,每个柱子的水位都被其左右两侧的最大值精确覆盖。
四、关键步骤拆解(以示例 1 为例)
ini 代码解读复制代码初始状态:
left=0, right=11, leftMax=0, rightMax=0, ans=0
Step 1:
height[0]=0 < height[11]=1 → 左指针移动
ans += 0 - 0 = 0 → ans=0
left=1
Step 2:
leftMax=1(height[1]=1)
height[1]=1 < height[11]=1 → 移动左指针
ans += 1 - 1 = 0 → ans=0
left=2
...(中间步骤省略)
最终累计 ans=6
五、复杂度分析
- 时间复杂度:O(n),仅需一次遍历。
- 空间复杂度:O(1),仅需常数空间。
六、方法对比与适用场景
| 方法 | 时间复杂度 | 适用场景 | 优势 |
|---|---|---|---|
| 分层双指针法 | O(H * n) | 高度较低且分布均匀 | 思路直观,易于理解 |
| 优化双指针法 | O(n) | 任意高度分布 | 高效,处理大规模数据 |

七、总结
优化后的双指针法通过动态维护左右最大值,将问题转化为单次遍历的线性操作,完美解决了分层法的性能瓶颈。其核心在于利用短板效应和贪心策略,以最小的时间复杂度完成计算。理解这一算法,不仅能够高效解决接雨水问题,更能深入掌握双指针与动态规划的联合应用。


评论记录:
回复评论: