前言
差不多有一个月没写文章了,这段时间一直在攻克DFS和BFS,最近学了前缀和&差分,今天来和大家分享一下学习的经验,嘻嘻嘻~0v0......

一维前缀和
我相信大家在高中时期一定学习过数列以及数列求和吧! Well~,看起来高大上的前缀和,其实就是数列求和。假设有一数列 An,以及其求和数列 Sn,那么则会有以下的关系:

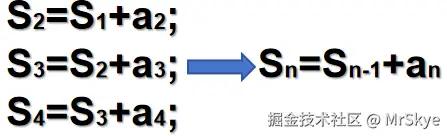
在这里,我们把S[i]叫做a[i]的前缀和。 利用S[i-1]、S[i]和a[i]的关系,我们可以很快地求出a数组对应的每一项的前缀和。
那么将这两个序列放进程序中就会是:
C 代码解读复制代码#include
若n=10,给a[i]赋值1~10;结果为:
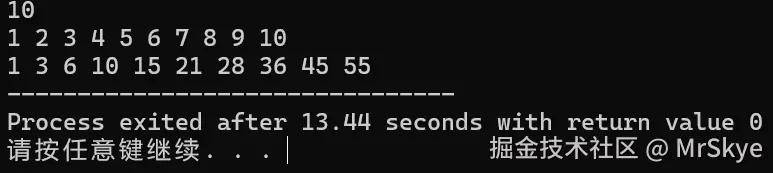
例题1—— 一维前缀和 from Acwing
来一道题练练手吧!
输入一个长度为 n 的整数序列。 接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例:
代码解读复制代码5 3 2 1 3 6 4 1 2 1 3 2 4
输出样例:
代码解读复制代码3 6 10
暴力?直接解题?
如果我们不知道有前缀和这个东西时,在看到这一题,肯定很想用暴力直接解题。也就是循环一遍先赋值,再循环一遍利用一个变量从a[l]一直加到a[r], 当然这也是一种方法,最简单直接的方法,但是做题的时候我们要注意数据的大小,在此题中n,m<10^5,如果在内容中用了双重循环的话,时间复杂度会变为O(n^2),计算次数会成为10^10,几乎就是计算机1s内计算的极限了,这个时候就会超时了。
而利用前缀和可以极大地减少计算次数。
例题答案
代码如下:
C++ 代码解读复制代码#include
更多练习题
一道题还不过瘾吧?嘻嘻嘻,我给你准备了好多练习题,都不是很难,快来做♂一做♂吧!

# [ABC339C] Perfect Bus From Atcoder. 提示:请记得把数组开大一点。
# 投票 (Voting) 翻译更正: 有 n 个人投票,每个人有参数xi,yi, 第 i 个人只会在 [i−xi,i] 区间内的人投了不少于yi 个赞成票时赞成,否则反对。 请求出多少人投赞成票。
(因为翻译问题我WA了很长时间,题目的翻译版本区间即 [i−xi+1,i] 是不对的,应该为 [i−xi,i] )
提示:合并同类项。
较难的题
二维前缀和
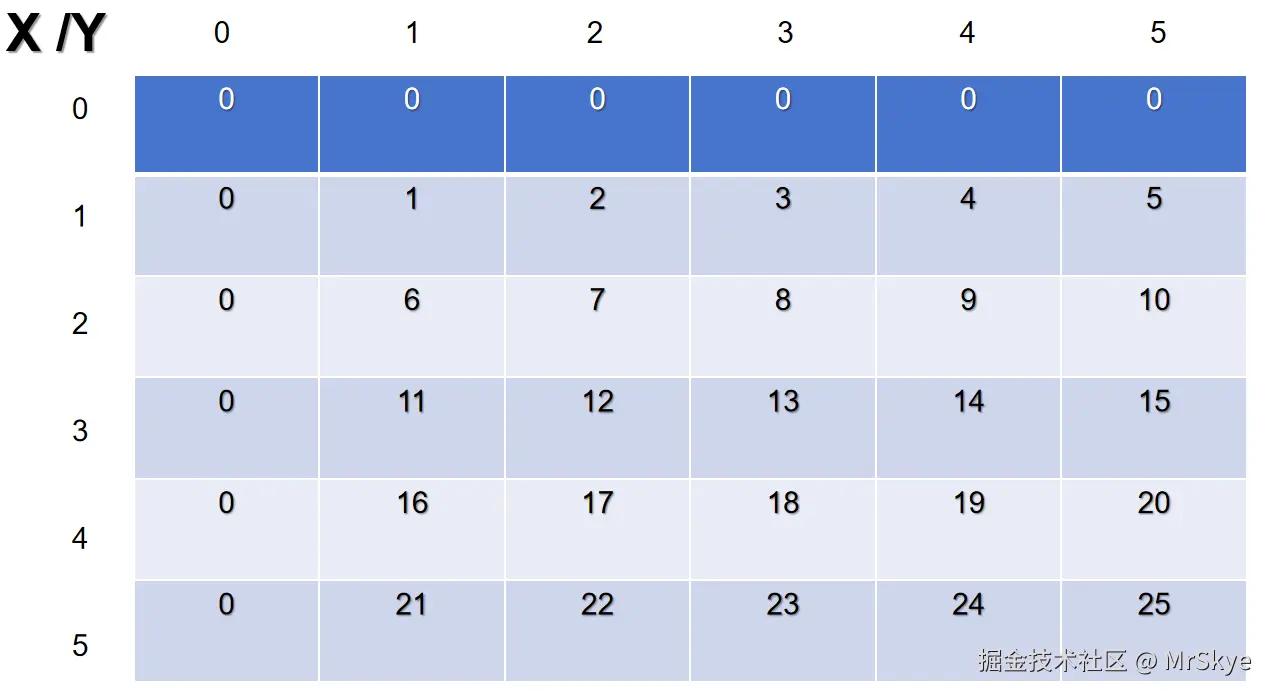
OK,baby~,既然有一维前缀和,那肯定就有二维前缀和咯。我们假设数组a[][], 以及其前缀和数组presum[][], 你猜猜下面这个矩阵各个元素的前缀和该怎么求~ c v c!
 嘻嘻嘻,我一猜你就是没头脑,然后你就成不高兴了,哈哈哈啊哈哈。
嘻嘻嘻,我一猜你就是没头脑,然后你就成不高兴了,哈哈哈啊哈哈。
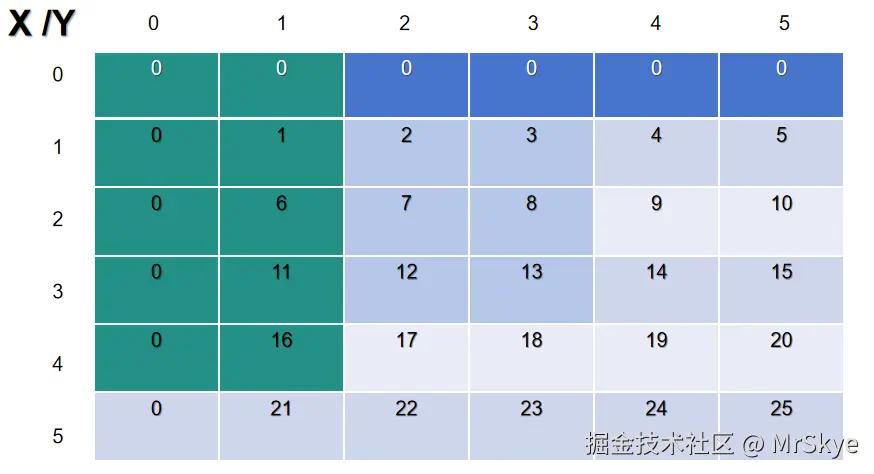
 其实,二维数组前缀和的求法,就是一个方形矩阵,从(0,0)到(x,y),覆盖的所有格内的数相加,就是(x,y)这个点的前缀和,比如(3,3)吧!(3,3)这个点的前缀和就是下面橙色部分相加。
其实,二维数组前缀和的求法,就是一个方形矩阵,从(0,0)到(x,y),覆盖的所有格内的数相加,就是(x,y)这个点的前缀和,比如(3,3)吧!(3,3)这个点的前缀和就是下面橙色部分相加。
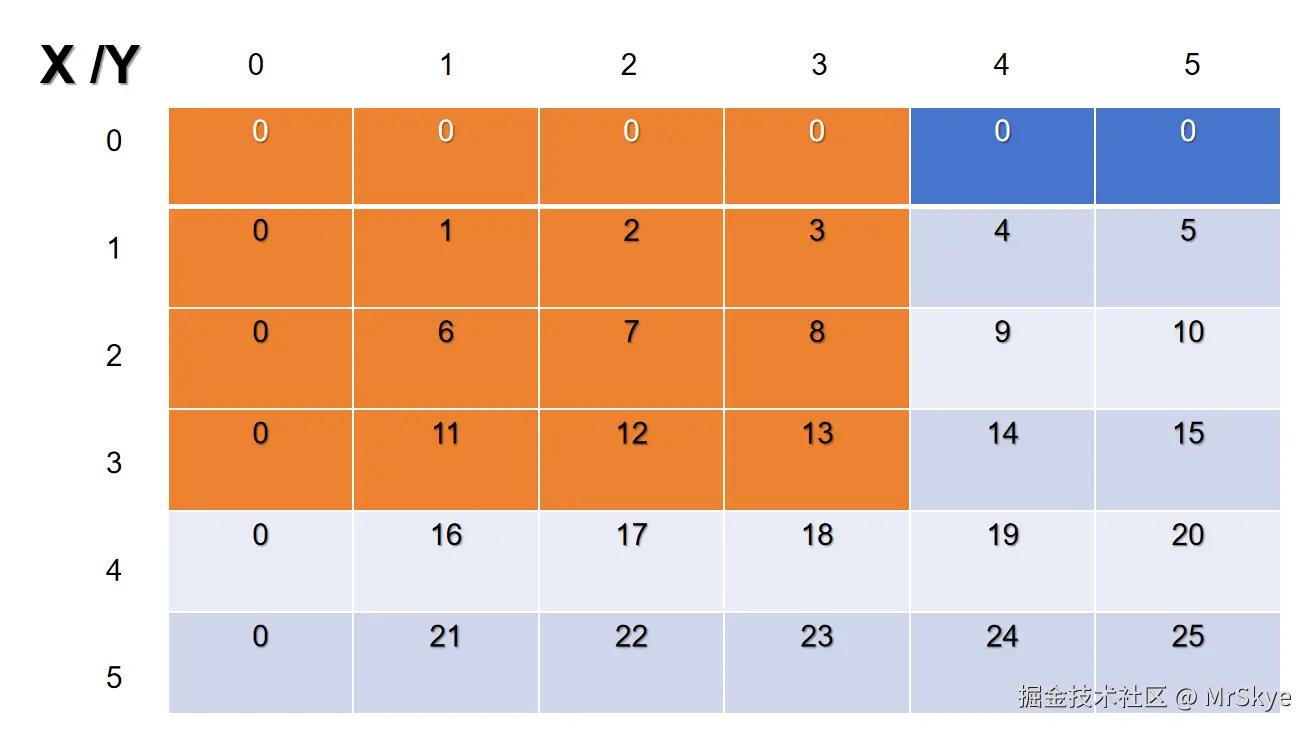 那么(3,3)的前缀和presum[3][3]=1+2+3+6+7+8+11+12+13=63;
那么(3,3)的前缀和presum[3][3]=1+2+3+6+7+8+11+12+13=63;
再举个例子,(1,4),presum[1][4]=1+6+11+16=34;
求二位前缀和
当然,让我们把这些元素一个个加起来肯定不现实,其实每个元素的前缀和都和他周围元素的前缀和有关系。这里我直接给出公式,大家看图理解一下。 公式:presum[i][j]=presum[i][j-1]+presum[i-1][j]-presum[i-1][j-1]+a[i][j];
图中任何一个点都适用此公式!!!!
例子:presum[4][3];
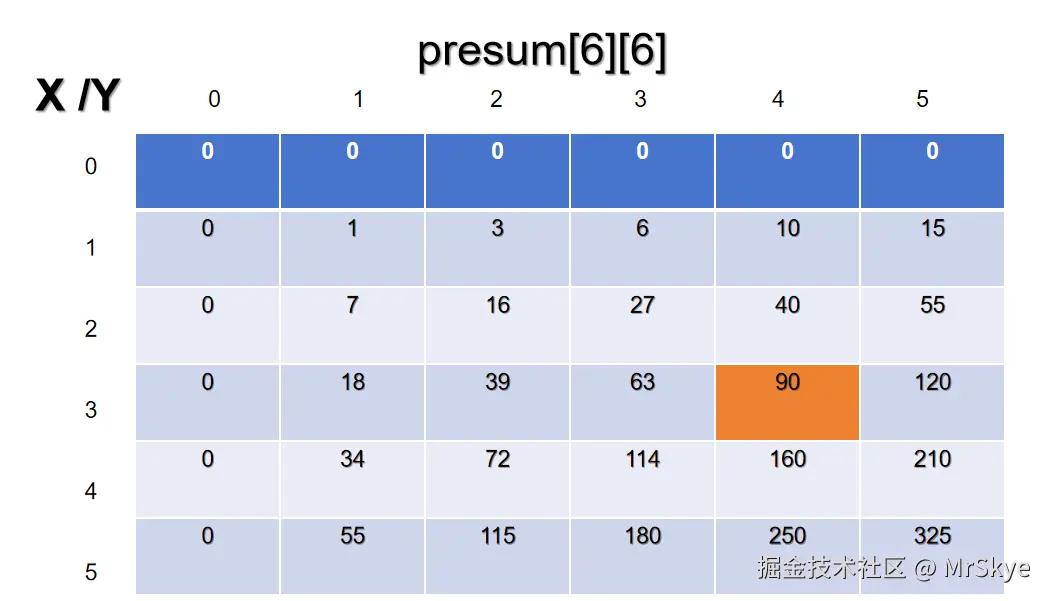
 黑色:presum[3][2]
黑色:presum[3][2]
绿色:presum[3][3]
黄色:presum[4][2]
红色:presum[4][3]
presum[4][3]=presum[3][3]+presum[4][2]-presum[3][2]+a[4][3];
也就是说每个点的前缀和=本身的值+左边和上边的前缀和值-左斜对过前缀和的值
既然如此,那么我们就能求出来每一个点的前缀和了。如下:
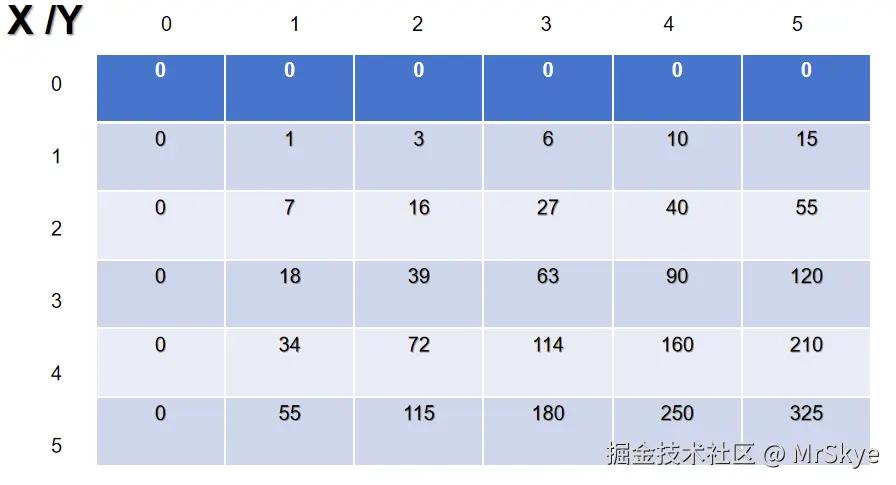
为什么从(1,1)开始赋值
当然大家可能看到了一般这里都从(1,1)开始赋值,因为求前缀和需要用到其元素之前的元素,如果用(0,0)作为起始点,就会越界带来一些不必要的麻烦, 所以在此建议大家以后求前缀和都从(1,1)开始赋值。
如何求取子矩阵的值?
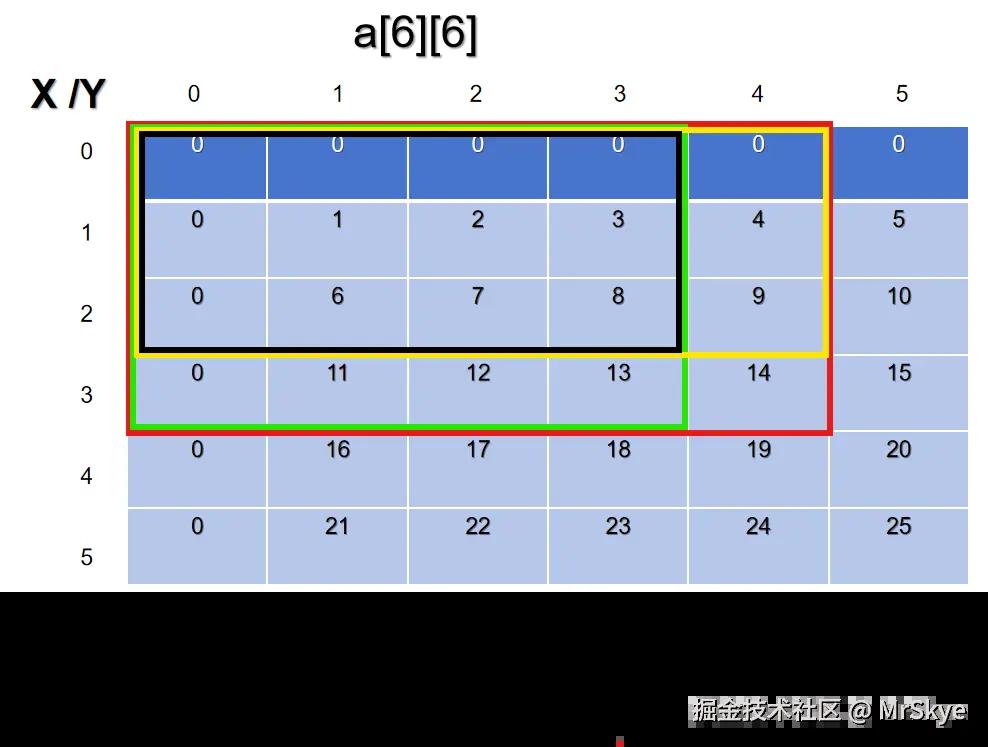
难道真的有题目会这么简单只让求取一个总的前缀和矩阵吗?NoNoNo,absolutely 闹特~ 我们还要去求子矩阵的和,比如让求 (2,2)到(3,4)的和。
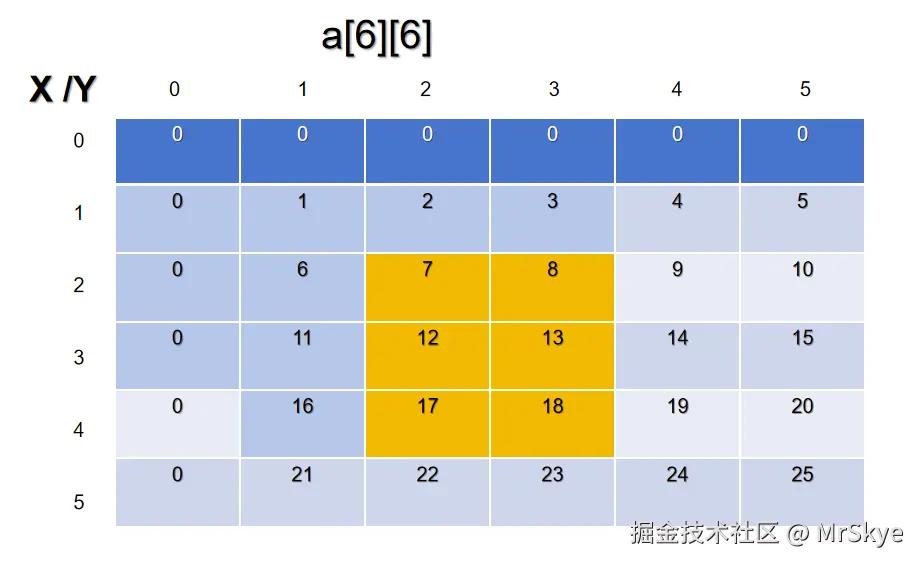 难道这个时候要一个个加起来?NO,让我们联合着presum[6][6]来一起看看。
难道这个时候要一个个加起来?NO,让我们联合着presum[6][6]来一起看看。
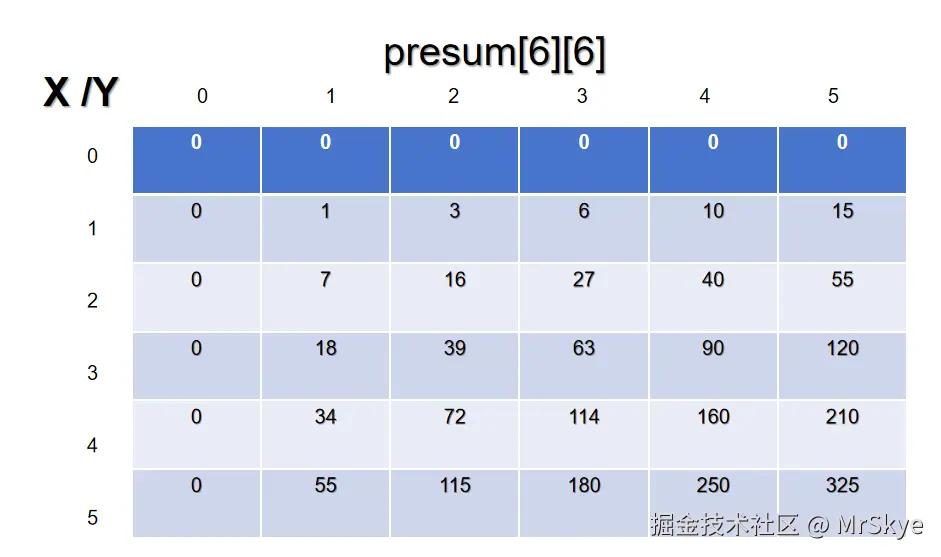 presum中的每一个点,都对应着在a[6][6]中,从(0,0)到那一个点所连成的矩阵之和。我们可以利用这一个性质来计算子矩阵的和。
presum中的每一个点,都对应着在a[6][6]中,从(0,0)到那一个点所连成的矩阵之和。我们可以利用这一个性质来计算子矩阵的和。
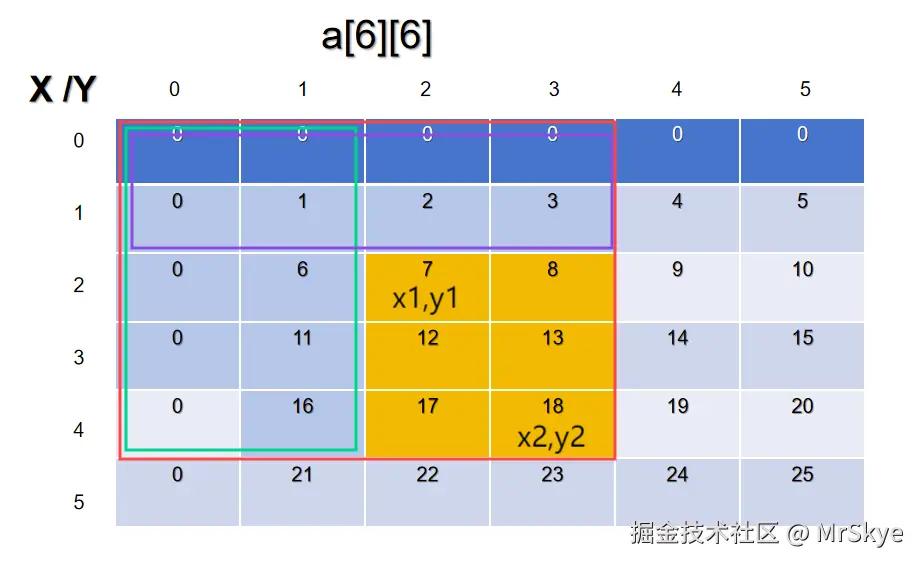 如图所示,我们可以这样求解:
如图所示,我们可以这样求解:
红色=presum[3][4],
绿色=presum[1][4],
紫色=presum[3][1],
为了求得目标黄色块内的答案,我们可以用红色-绿色-紫色+presum[1][1],因为我们减去绿色和紫色的时候,多减了一次presum[1][1]的值,所以要加回去。这样放在presum数组中,矩阵和子矩阵的关系就为:
res=presum[x2][y2]-presum[x2][y1-1]-presum[x1-1][y2]+presum[x1-1][y1-1]
一定要理解!!!!!
例题1————二维前缀和
相信你已经明白二维前缀和以及子矩阵的求法了,快来做一道题试一试吧。
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q 行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000
1≤q≤200000
1≤x1≤x2≤n
1≤y1≤y2≤m−1000≤矩阵内元素的值≤1000
输入样例:
代码解读复制代码3 4 3 1 7 2 4 3 6 2 8 2 1 2 3 1 1 2 2 2 1 3 4 1 3 3 4输出样例:
代码解读复制代码17 27 21
例题答案
C++ 代码解读复制代码#include
结尾
这一期就是这样了,前缀和一定要去理解,记得去洛谷力扣多找一些题目去做。下一期是差分,拜拜~~


评论记录:
回复评论: